组合摆振下金属颗粒的分层模拟研究*

2022-06-24张浩强卢森幸

机械工程与自动化 2022年3期

张浩强，蔡柳，卢森幸

(河池学院，广西宜州 546300)

0 引言

随着我国工业水平的不断提高，对各种金属的产量也提出了较高的要求。多种金属的冶炼，均是以除杂的金属矿石颗粒为冶炼原料，因此需要对从矿山开采、破碎后的金属矿石颗粒进行分选除杂。以黑钨矿石的粗选工艺为例，大多采用传统的人工分选，存在分选工作效率低、分选效果良莠不齐、人工成本高的问题[1]。颗粒的振动分选在物质分选上有着非常广泛的应用，在南朝的宋时期就出现了关于振动分选的文字记载。《世说新语》中有“簸之扬之，糠秕在前；洮之汰之，砂砾在后”，以农业应用实例对振动分选的过程和结果进行了描述[2]。应用振动分选矿石颗粒中的杂质，可以提升分选效率，提高分选效果，降低生产成本。

1 振动分选影响因素及原理

1.1 振动分选影响因素

颗粒实现振动分选需要具备相关条件，两种或多种颗粒需满足各种不同属性，包括颗粒直径、颗粒密度等，当颗粒直径和密度存在不同时即可通过振动实现分层分选。振动运动按照运动平面及运动方式可以分为水平直线振动、竖直直线振动及圆周摆动振动，不同的振动方式往往产生不同的分层效果。例如竖直振动的竖直容器可实现两种不同直径颗粒的分层，其中大直径颗粒集中在颗粒层的上部，小直径颗粒则集中在颗粒层的下部，这种现象称为“巴西果效应”[3，4]。然而改变振动的频率和振幅又会出现大直径颗粒在颗粒层的下部，小直径颗粒则集中在颗粒层上部的现象，这种现象称为“反巴西果效应”[5]。再适当改变振动频率和振幅可能会出现颗粒层分三层的现象，大直径颗粒在颗粒层中间，小直径颗粒分布在颗粒层的上、下两端。由此可见振动的频率和振幅对振动分层有较大的影响。

众多学者已经对水平直线振动、竖直直线振动及圆周摆动振动这类单独运动振动进行了详尽的研究，但在多种运动的组合振动形式上还鲜有涉及。本文以研究组合振动方式中的水平振动频率、振幅及摆动振动频率、振幅对金属颗粒振动分层分选效果的影响为目的，从而为金属颗粒分选装备的研究奠定理论基础。

1.2 金属颗粒振动分选原理

金属颗粒分层运动过程依次为金属颗粒的相互碰撞、金属颗粒间隙的产生、金属颗粒的滑移、不同属性金属颗粒产生速度差、不同属性金属颗粒交换位置、金属颗粒间隙填充消失、金属颗粒位置稳定等，金属颗粒在振动运动过程中将受到摩擦力、重力、惯性力、接触力等多个力的共同作用，其中金属颗粒间的接触力包括法向接触力和切向接触力，采用Hertz-Mindin无滑移接触模型分析两颗粒之间的碰撞[6-8]。

1.2.1 颗粒的法向接触力

两颗理想金属颗粒碰撞时的接触面极小且不发生黏连，在接触面上两颗粒发生的均为弹性变形，弹性变形产生的应力垂直于弹性变形面指向颗粒的球心，定义两颗粒的直径分别为R1、R2，两颗粒的球心位置矢量分别为r1、r2。

接触颗粒的法向接触力Fn(N)计算公式为：

(1)

其中：R*为两颗粒的有效半径，mm；E*为两颗粒的有效弹性模量，MPa；α为两颗粒的法向重叠量，mm；a为两颗粒的接触面半径，mm。且：

(2)

(3)

(4)

(5)

其中：υ1、υ2分别为两颗粒的泊松比；E1、E2分别为两颗粒的弹性模量。

1.2.2 颗粒的切向接触力

两金属颗粒发生切向接触时，接触面沿着圆周切线方向滑移。两颗粒接触的切向位移和切向力分别为δt、Ft，当两颗粒产生了Δδt大小的切向位移增量，则会产生ΔFt的切向力增量。即：

ΔFt=8aG*θkΔδt+(-1)kμ(1-θk)ΔFn.

(6)

其中：μ为颗粒的静摩擦因数；G*为等效剪切模量；ΔFn为两颗粒的法向力增量；k=0，1，2，表示切向力加载、卸载、再加载;θk由下式计算：

(7)

其中：Ftk为颗粒接触切向力，Ft1为接触卸载后颗粒切向力，Ft2为接触重新加载后颗粒切向力。

2 金属颗粒在组合摆振下的分层模拟仿真

2.1 几何模型建立

为研究组合摆振下金属颗粒的分层行为，实现利用摆振高效完成金属颗粒的分选，采用计算机仿真技术，利用EDEM软件对组合摆振下的金属颗粒分层行为进行模拟。本文探究组合振动方式对颗粒分层的效果，因此建立两种直径相同、密度不同的球形颗粒，其中颗粒1为钨金属矿石颗粒(设定浅色)，颗粒2为杂质土质颗粒(设定深色)，颗粒的具体模型尺寸如图1所示。组合摆振的振动容器为半圆形料槽，其几何尺寸为直径150 mm、宽80 mm、壁厚2 mm，料槽形状如图2所示。料槽的组合振动运动方式为以圆心为轴的往复圆周摆动运动和沿水平方向的往复直线运动。

图1 颗粒模型尺寸

图2 料槽模型

2.2 振动分层效果评价方法

为更加直观地体现颗粒的分层效果，采用金属颗粒的体积浓度作为分层效果的衡量指标，将t时刻选取区域x内所包含的金属球的单位体积浓度记为Cj，体积浓度的具体表达式为:

(8)

其中：Vj为选取区域x内金属颗粒的总体积；Vi为选取区域内第i种颗粒的体积；n为选取区域内颗粒的种类数，颗粒有2种。

2.3 组合摆振仿真过程

应用离散元软件EDEM模拟金属颗粒球与土质颗粒球的组合摆振分层过程，建立了两种颗粒模型后，根据参考文献[9-11]设置金属颗粒、土质颗粒及钢质料槽的物性参数及接触参数。颗粒材料及料槽结构材料的物性参数设置如表1所示，颗粒材料与颗粒材料及颗粒材料与料槽材料的主要接触参数如表2所示。

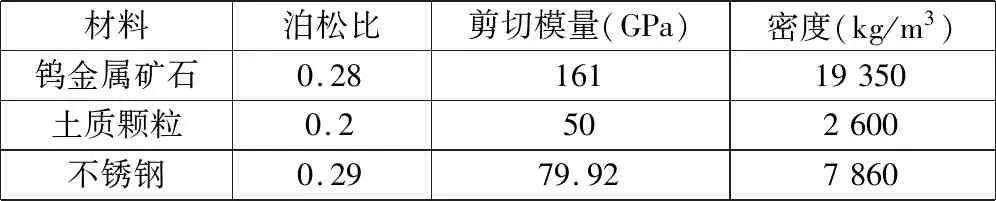
表1 颗粒材料及料槽的物性参数

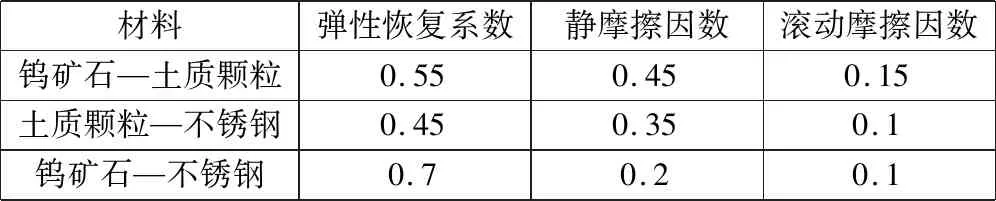
表2 材料接触参数

料槽的组合振动运动分为以圆心为轴的往复圆周摆动运动和沿水平方向的往复直线运动，其中以圆心为轴的往复圆周摆动运动通过频率和振幅(角度)定义，沿水平方向的直线振动运动通过频率和振幅(位移)定义。振动中过小的频率和振幅难以使分层效果明显，且分层过程较为缓慢；而较大的振动频率和振幅易使颗粒运动幅度过大产生飞溅，同时颗粒的运动效果还与材料的接触参数有极大的关联。在明确材料接触参数后，定义6组往复摆动运动和往复直线运动参数，如表3所示。根据学者对金属颗粒和塑料的单种运动振动分层模拟仿真，在30 s左右颗粒出现较明显分层现象，因此本次研究的仿真时间设置为50 s，保证仿真时间不影响仿真结果的准确性。

表3 组合运动参数

3 仿真结果及分析

3.1 仿真结果

仿真过程中金属颗粒和土质颗粒的分层效果如图3所示，并得到不同运动参数的分层效果即金属颗粒体积浓度随时间变化曲线，如图4所示。

图3 颗粒的分层过程

3.2 组合摆振分层结果分析

由图4可以看出：第2组、第5组的组合运动振动分层过程较为稳定，且最终金属颗粒体积浓度较高。由第3组和第6组可以看出，摆振频率较大时，颗粒的分层行为不稳定，反映出颗粒受料槽高频率运动的影响较大，颗粒运动得极不稳定，颗粒的位置转换较为频繁，导致所选区域内两种颗粒分层效果降低。

图4 颗粒的分层效果

由第1组、第2组、第4组、第5组对比第3组、第6组可以得出组合振动的振动频率和振动振幅并非越大越好，频率为6 Hz～8 Hz较适宜振动分选。由第1组、第4组对比可以得出摆动振幅8°相较于12°振动分选效果较好。由第2组、第4组可以看出往复摆动频率8 Hz、摆动角度10°、往复直线运动频率8 Hz颗粒的振动分层较为平稳，且直线运动幅值2 mm相较于4 mm更早完成分层行为，且最终金属颗粒的体积浓度较高。