智能阀门定位器的仿人智能PID控制策略研究

程予任,叶灵宋,余昭旭

(1.华东理工大学信息科学与工程学院，上海 200237；2.上海自动化仪表有限公司，上海 200072)

0 引言

调节阀是一种过程控制仪表，普遍应用于现代工业生产过程。阀门定位器作为气动调节阀的配套设备，对调节阀的过程控制性能起到至关重要的作用。定位器能够控制气动直行程或角行程执行机构，通过对调节阀阀杆的精确定位控制，实现对管道内流体流量的调节或通断，从而尽可能保证系统运行安全和控制品质[1]。它能优化调节阀的流量特性、加快调节速度、减少控制信号的传递滞后、降低阀杆移动的摩擦力和阀芯不平衡力导致的影响，以及提高调节阀系统的控制精度和响应速度。这些特点对于现代工业生产过程的平稳、安全有着重要意义，并且能够节约最终用户的成本[2]。

智能阀门定位器是目前阀门定位器的主要研究方向和未来发展趋势。正是由于其相较于传统阀门定位器有着明显的优化和改进,更适合现代工业生产过程的需要。智能阀门定位器的控制算法是实现调节阀精确定位控制的核心。

调节阀在运行时会受到阀杆移动的摩擦力和阀芯所受流体力等时变力。同时，类型不同、负载改变、气源压力稳定性差以及调节阀的安装也会对其产生影响，使系统具有非线性、大惯性或大滞后等问题。所以，对被控系统建立统一的数学模型难度较大[3]，并且其控制算法始终是气动控制系统的研究难点。目前，气动阀门定位器中普遍使用的控制算法有比例积分微分(proportional integral differential,PID)控制和模糊控制。文献[4]对智能阀门定位器的控制算法进行研究，实现了线性化方法和分段比例积分(proportional integral,PI)这两种可变脉冲宽度调制(pulse width modulation,PWM)占空比的方法,在小范围阶跃控制过程中,能够加速阀位启动、提高小范围阶跃控制速度。但是，该方法只能改善小范围阶跃的调节速度。文献[5]在模糊自适应PID控制的基础上，结合了Smith预估控制方法。Smith预估控制方法能够补偿控制对象纯滞后性,而模糊PID算法能够使系统具有较小的超调量和较好的适应性。但是该方法未考虑如何提高阀门运动的快速性。

本文提出了一种智能阀门定位器的仿人智能PID控制方法。该方法根据误差的大小和变化趋势设计了仿人智能控制规则，并根据仿真结果进行显示。该控制算法能够明显加快调节阀的响应速度，同时输出响应曲线平滑、无明显波动，从而有效地改善了调节阀的速度和精度、提高了系统的鲁棒性。

1 智能阀门定位器

1.1 智能阀门定位器的发展

水、汽、油等流体与工业生产密切相关。流体在工业生产过程中的应用必然需要管道设施。阀门对于管道设施而言至关重要。阀门定位器是阀门控制调节必不可少的部件，可改善调节阀的控制效果，以及确定调节阀系统的控制精度、响应速度[6]。在一些应用领域，对阀门的控制并不单纯是普通的开关控制，同时涵盖了开度大小的调节以及频繁的控制动作。因此，阀门定位器的智能性和适应性必须满足更高的要求。在20世纪 90 年代，过程控制发展水平的提升以及计算机技术的日益成熟，推动了带微处理器的智能仪表的发展。于是，压力变送器、温度变送器等现场变送器产生了很多改进和升级，智能阀门定位器也应运而生[7]。由于智能阀门定位器可靠性高、精度高，能够进行功能扩展和通信，对于当今工业过程控制中网络化、集成化、智能化的发展要求具有更高的适应性。

1.2 智能阀门定位器的工作原理

智能阀门定位器一般有电气转换单元、阀位检测反馈单元和中央控制单元三个部分[8]。智能阀门定位器原理如图1所示。

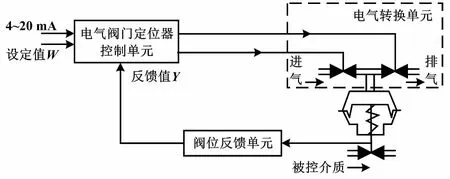
图1 智能阀门定位器原理图

智能阀门定位器在高度集成的微控制器的基础上，采用数字化技术进行数据处理和决策生成，利用电气转换器实现电信号与气动信号的转化，实现了电气转换和精确定位的功能[9]。在智能阀门定位器控制系统中，4～20 mA输入信号与阀位反馈信号通过阀门定位器的控制单元处理，根据两者偏差输出脉冲控制信号到电气转换单元(压电阀)，控制电气转换单元(压电阀)的输出气压改变，可控制气动调节阀的阀杆运动。同时，位移传感器检测到阀杆的行程并反馈到阀门定位器的控制单元，实现闭环控制。

2 控制器原理与设计

2.1 仿人智能PID控制原理

仿人智能PID控制器分为仿人智能控制和PID控制两部分。根据误差大小以及误差变化趋势自适应调节PID控制参数，可达到抑制动态误差、改善控制性能的效果。仿人智能PID控制器的本质为效仿人类的思维过程和智能行为进行决策和控制，不需要了解对象的结构和参数，不依赖于对象的数学模型，而是利用受控对象和控制规律的知识和经验进行推理和变换控制策略[10]。仿人智能PID控制器结构如图2所示。

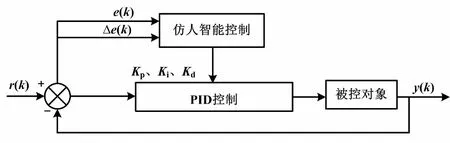
图2 仿人智能PID控制器结构图

2.2 仿人智能PID控制器设计

常规增量式PID控制器的输出为：

u(k)=u(k-1)+{Kp[e(k)-e(k-1)]+Kie(k)+

Kd[e(k)-2e(k-1)+e(k-2)]}

(1)

式中：u(k)为第k次控制器的输出；u(k-1)为第(k-1)次控制器的输出；e(k)为当前采样时刻的误差值；e(k-1)、e(k-2)分别为前一个和前两个采样时刻的误差值；Kp、Ki、Kd分别为PID控制器的比例、积分、微分系数。

常规PID是一种线性控制器。参数整定是PID控制系统设计的主要内容。对于调节阀系统这种非线性系统而言，这种控制算法不能妥善地解决系统稳定性、准确性与快速性之间的矛盾。

仿人智能控制的设计依据是调节阀流量控制相关的一系列经验规则，根据控制系统的误差e(k)和误差的增量Δe(k)进行设计。把e(k)·Δe(k)和Δe(k)·Δe(k-1)这两个特征量作为调节依据，在线实时变换控制策略，调节控制参数。其中：Δe(k)=e(k)-e(k-1)；Δe(k-1)=e(k-1)-e(k-2)。

典型的二阶系统单位阶跃响应曲线如图3所示。

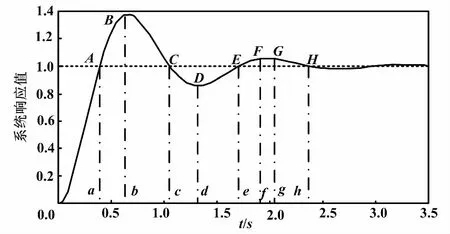
图3 典型的二阶系统单位阶跃响应曲线

当误差的绝对值非常大时，不需要考虑误差的变化趋势，直接采用Bang-Bang控制就可以使得系统具有较快的响应速度。此时，控制器的输出按照最大输出，以便迅速减小误差。

当误差较小时，如果e(k)·Δe(k)>0(如AB段或CD段),表明误差处于增大的过程中。此时，控制器倾向于实施PID作用,需要改变误差绝对值变化的方向、增大反向控制作用、减小超调，以达到迅速减小误差绝对值的目的。如果e(k)·Δe(k)<0(如BC段或DE段),表明误差绝对值处于减小的过程中。此时，考虑使PID控制器保持输出不变，使得系统通过惯性的作用过渡到稳态。

当Δe(k)·Δe(k-1)>0,表明误差不存在极值，比如在A、C、E时刻。当Δe(k)·Δe(k-1)<0，表明误差存在极值，比如在B、D时刻。此时，将以上两个特征量相结合就可以推断系统误差的变化趋势。比如：当某一时刻e(k)·Δe(k)>0且Δe(k)·Δe(k-1)<0，则该时刻后的误差从增大变为减小趋势。当某一时刻e(k)·Δe(k)<0且Δe(k)·Δe(k-1)<0，则该时刻后的误差从减小变为增大趋势。

在FG段,Δe(k)=0,但是e(k)≠0,表明系统误差在此时为一个定值,应当加上积分作用,从而达到快速消除误差的目的。

当误差绝对值很小时，它可能是由系统静差导致。此时，应当引入积分作用，以减小系统的稳态误差。

仿人智能控制的原型算法为：

(2)

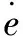
将仿人智能控制与PID控制相结合，设计控制器。

①建立特征模型。

φ={φ1,φ2,φ3,φ4,φ5,φ6,φ7,φ8,φ9}=

(3)

式中：M1和M2为两个误差界限，M1>M2；M3为误差的极小值。

②构建控制策略。

ψ={ψ1,ψ2,ψ3,ψ4,ψ5,ψ6,ψ7}=

(4)

式中：u(k)为第k次控制器的输出；u(k-1)为第(k-1)次控制器的输出；sgn为符号函数；Umax为控制器开环输出；k1为增益放大系数，k1>0；k2为增益抑制系数，0

③构建控制模态集：

Ω={Ω1,Ω2,Ω3,Ω4,Ω5,Ω6,Ω7,Ω8}=

(5)

3 仿真结果分析

气动调节阀的阀门特性能够表示为工业控制过程中普遍的一阶惯性时滞对象[11]。调节阀控制对象的传递函数为:

(6)

给定阶跃信号，采用仿人智能PID控制器、传统PID控制器和模糊PID控制器进行仿真试验。设置参数Kp=2.9、Ki=5.6、Kd=0.66，且模糊PID控制器的模糊规则设计参考文献[12]。仿真运行时间设置为30 s。

控制系统阶跃响应及误差曲线如图4所示。由图4可知：在仿人智能PID控制下，阶跃响应达到目标值的调整时间为2.61 s,系统无超调；在传统PID控制下，调整时间为5.41 s，其超调量为1.4%;在模糊PID控制下，系统无超调，但调整时间为3.98 s。由此可知，相较于传统PID控制器和模糊PID控制器，仿人智能PID控制器无超调且响应速度更快、控制性能更好。

图4 控制系统阶跃响应及误差曲线

为了检验控制器的鲁棒性，将控制对象转化为：

(7)

在控制器的控制参数不变的情况下，控制方法的阶跃响应及误差曲线如图5所示。由图5可知：在仿人智能PID控制下，阶跃响应达到目标值的调整时间为3.08 s,系统无超调；在传统PID控制下，调整时间为7.33 s，其超调量为4.7%；在模糊PID控制下，调整时间为7.62 s，其超调量为9.3%。由此可知，仿人智能PID控制器在对象变化后，较之传统 PID 控制器和模糊PID控制器仍然具有更好的稳态性能和动态性能，鲁棒性也更强，更适用于智能阀门定位器系统的控制。

图5 控制系统鲁棒化阶跃响应及误差曲线

4 结论

本文介绍了智能阀门定位器的发展过程以及工作原理，基于调节阀非线性、大惯性以及大滞后的特点，提出了一种新的仿人智能PID控制方法，并将其应用于智能阀门定位器中。根据调节阀流量控制的一系列经验规则，设计了仿人智能控制规则，并通过MATLAB进行仿真验证。仿真结果表明，该控制算法能够实现精确控制,与传统的PID控制算法和模糊PID控制算法相比具有更快的响应时间、更好的鲁棒性，是一种性能更优越的智能阀门定位器控制算法。