保护隐私的有理数科学计算

刘旭红，孙晨

（上海体育学院经济管理学院，上海 200438）

0 引言

安全多方计算（SMC，secure multiparty computation）是关于一组互不信任的参与者在保护各自隐私数据的前提下进行协同计算的问题，SMC要确保各参与者输入数据的私密性以及计算结果的正确性。随着信息时代数据安全性越来越受到重视，安全多方计算成为国际密码学界的研究热点。

图灵奖获得者姚期智教授在文献[1]中首次提出安全多方计算问题，并引起国际密码学界的重视[2-3]，Goldreich等[4,5]对其进行了深入的研究，从理论上证明了任意的安全多方计算问题都是可解的，并给出了通用的解决方案。由于通用解决方案的效率很低，利用通用方案解决具体的计算问题一般是不可行的，考虑到实际应用场景和计算效率与通信效率的问题，需要针对具体问题研究具体的解决方案。基于上述学者的研究理论，许多密码学研究人员不断提出新的具有实际应用前景的安全多方计算问题及其解决方案，推进了安全多方计算研究的发展。目前所研究的问题有保密信息比较[6-7]、保密数据挖掘[8-9]、保密几何计算[10-11]、保密数据查询[12-13]等。

保密比较相等问题和保密集合计算问题是基本的安全多方计算问题，保密比较相等问题是保密信息比较中重要的基础问题并得到了广泛的研究[14-18]，其对集合问题的保密计算具有重要的基础作用。集合问题在保密数据挖掘、保密统计分析、保密几何计算等方面有重要的应用，其中保密判定元素与集合的关系[19-21]是集合保密计算中的基本问题。文献[14,15]基于第三方参与者设计了整数集上的保密比较相等协议，计算复杂性较高。文献[16]提出了一个有理数阈值密码系统，基于所提出的门限方案，构造了分布式有理数相等测试协议，协议中需要多个参与者共同参与保密判定两个有理数的相等问题，且计算复杂性较高。文献[17]利用单项哈希函数解决了两个整数相等问题和整数向量相等问题，计算效率较高，但无法抵抗穷举攻击。文献[18]利用Paillier公钥加密算法解决了有理数相等问题，相比文献[16]计算效率有所提高。文献[19]应用不经意多项式计算设计了整数集上元素与集合关系的保密判定协议，该方案借助于Paillier公钥加密体制，计算复杂性较高。文献[20]利用对称加密体制和异或运算设计了高效的整数集上元素与集合关系的保密判定协议，但泄露了集合元素的取值范围，具有一定的局限性。文献[21]应用Paillier加密算法首次解决了有理数域上元素与集合关系问题。

上述相关工作为研究更高效更广泛的安全多方计算奠定了基础，根据现有相关问题的多个解决方案，分析每个解决方案的优缺点，可以进一步设计更加安全高效且适用范围更广的解决方案。已有的关于保密比较相等问题和保密计算集合问题的研究大多局限于整数范围，现有的有理数域上的解决方案计算效率低，且无法应用于实际中有理数域上相关问题的保密计算，限制了相等问题和集合问题的实际应用场景。

有理数不仅在现实生活中有广泛的应用，在生物学、气候学、化学等领域中的应用更为广泛，尤其这些领域的研究工作讲究准确性，无误差性。例如，在医疗保健方面，不仅需要准确诊断病人的健康情况，而且需要确保病人的健康状况和其他个人信息的安全性。由于大多数医疗数据（如血糖、胰岛素和c肽水平）是有理数[22]，而传统的密码系统只能加密整数，这将影响数据的准确性以及计算效率，从而影响决策和导致错误诊断。基于上述相关问题，文献[23]提出了允许用户将有理数外包给云服务器进行存储和处理的一种新的高效隐私保护外包计算框架，为继续研究有理数域上安全多方计算问题提供了研究背景和意义。

在计算几何方面，有理数的应用也较广泛[24-25]，举例如下。① Alice拥有一条直线l1:y=k1x+b1，Bob拥有一条直线l2:y=k2x+b2，Alice和Bob希望保密判定两条直线是否相交，则只需保密判定两条直线的斜率k1和k2是否相等，即保密判定两个有理数是否相等。② 在多边形相似的保密判定问题中，需要保密判定对应边是否成比例，通过归一化可以将问题转化为保密判定有理向量相等问题。③ 随着计算机网络的迅速发展，坐标定位在多个行业中的应用越来越普遍（侦查活动、手机App等）。假设在某项侦查活动中，Alice锁定了多个位置点，记为点集合U；Bob所在的位置坐标记为点u，Alice和Bob想要保密判定点u是否属于集合U，即保密判定二维空间的元素与集合关系。

上述相关问题中，多个研究对象需要用有理数或有理数集合进行描述，从而将问题抽象为有理数域上的安全多方计算问题。根据现有的安全多方计算协议，由于加密体制的限制，往往需要将计算几何问题转化到正整数集合上进行研究，导致计算复杂性高、适用性差。研究有理数域上的安全多方计算问题，通过有理数或有理数集合直接解决遇到的问题，或为解决问题提供新的途径，对安全多方计算的研究具有重要意义。

本文主要研究构造有理数域上相等问题和集合问题的保密计算协议，是有理数域上安全多方计算研究的基础。

本文的贡献如下。

1）利用有理数的分数表示形式，设计了关于有理数的一种全新的编码方法。该编码方案将任意有理数（数组）编码为整数，为有理数与整数之间的转换提供了一种新的思路。

2）将新的编码方案与单向哈希函数相结合，解决了有理数域上的相等问题和集合问题。

3）协议计算效率高，且适用范围广（整数集合和有理数集合均适用），可用于解决更多安全多方计算问题。

4）通过实例说明对于所设计的协议进行适当修改或推广应用，对更多的安全多方计算问题或实际应用问题可设计构造安全高效的解决方案。

1 预备知识

本节主要介绍下文研究中所需要的一些基本概念和基础知识[5]。

1.1 基本定义

（1）双方计算

双方计算是一个将任意给定的输入对映射为输出对的随机过程, 这个过程用函数表示为f:(x,y)→(f1(x,y),f2(x,y))。即对于每一个输入对(x,y)，输出对是随机变量(f1(x,y),f2(x,y))。记这样的函数为f=(f1,f2)。

（2）半诚实模型

安全多方保密计算问题的初期研究基本上是以半诚实模型为基础的。半诚实参与者是指在协议执行过程中按照协议要求忠实地履行协议的参与者，不会欺骗和泄露信息，但是会收集和保留在协议执行过程中获得的所有信息，在协议执行后试图根据这些信息推算出额外的信息。如果所有参与者均为半诚实参与者，这样的计算模型称为半诚实模型。由于半诚实参与者不对协议实施主动攻击，所以半诚实模型又称为诚实但好奇（honest-but-curious）模型或被动模型。文献[5]给出了一个由半诚实模型下安全协议直接编译获得恶意模型下安全协议的一般方法，因此半诚实模型下安全计算协议的设计是基本而重要的。本文主要研究半诚实模型下的两方计算问题。

（3）模拟范例方法

模拟范例方法是由Goldreich提出的，在安全多方计算协议安全性证明中广泛使用的证明方法，其证明原理为：如果每个参与者在实际执行协议过程中所获得的信息都可以通过自己的输入和输出进行模拟，而且模拟所得到的消息序列与实际执行过程得到的消息序列计算不可区分，就说明协议是安全的。如果一个多方计算协议能够进行这样的模拟，即说明所有参与者都不可能从协议的执行过程中得到其他参与者任何有价值的信息。这种证明安全性的方法是研究安全多方计算问题时普遍接受的模拟范例方法。模拟范例方法的具体描述如下。

假设参与双方计算的参与者为P1和P2，则

① 设f=(f1,f2)是一个概率多项式时间函数，π表示计算函数f的一个双方协议；

② 当输入为(x,y)时，在执行协议π的过程中Pi(i=1,2)的view信息序列记为

其中，ri表示参与者Pi产生的随机数，表示Pi收到的第j个消息；

③ 执行协议后，参与者Pi(i=1,2)获得的输出结果记为。

定义1半诚实模型下协议的安全性。对于上述函数f和协议π，如果存在概率多项式时间算法S1和S2，使

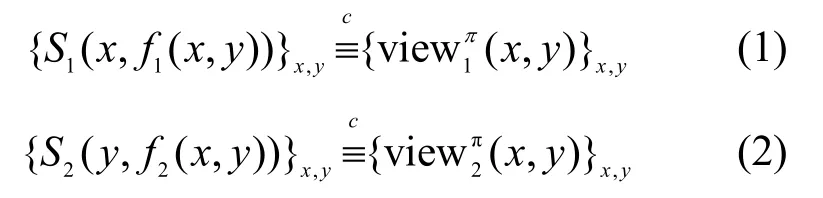
成立，则协议π保密地计算f，其中表示计算上不可区分。

要证明一个多方计算方案是安全的，就必须构造满足式(1)和式(2)的模拟器S1和S2。

1.2 字母表与连接运算

字母表是对象的有穷非空集合M，M中符号的n元组称作M上的字或字符串，M中所有字符串的全体记作M∗。例如，所有的自然数都是字母表{0,1,2,…,9}上的字符串，所有的二进制数都是字母表{0,1}上的字符串，字符串的连接定义如下。

其中，z=。对于给定的字符串u1,…,um∈M∗,就是把字符串u1,…,um一个接着一个放在一起所得到的新的字符串。

1.3 单向哈希函数的性质

单向哈希函数（简称为Hash函数）是密码体制中一类常用的公开函数，该函数将任意长度的消息映射成某一固定长度消息。它具有如下性质。

1) 给定消息m，很容易计算h=Hash(m)。

2) 给定h=Hash(m)，根据h计算其逆m=Hash−1(h)是困难的。

3) 给定m，要找一个消息m′，使Hash(m)=Hash(m′)是困难的。

4) 找出两个随机的消息m,m′，使Hash(m)=Hash(m′)是困难的。

5) 如果对m做微小的改变，即使只改变一个比特，变为m′，Hash(m)的值与Hash(m′)的值相比也会发生惊人的变化，至少改变一半位数的值。

进一步，根据单向哈希函数的性质可知，Hash(a)=Hash(b)但a≠b的概率为1/2|Hash()|。例如，在SHA-1算法中|Hash()|=160，如果利用SHA-1算法做单向哈希函数，Hash(a)=Hash(b)但a≠b的概率为1/2160。在一般应用中，如此小的出错概率是可以忽略不计的。

Hash函数具有上述特性，所以常被用于消息的完整性检测和消息认证。

2 编码方案

本节设计一种有理数的编码方法，以此方法，任一有理数（或有理向量）与一个十进制整数相对应。

2.1 有理数的编码

（1）有理数的编码方式

① 有理数的分数表示

对任一有理数w，首先按如下方式将其表示为唯一的分数形式（其中w1≥0,w2≥1 均为整数，s为符号位）。当0w≠时，要求12,ww互素，当w=0时，约定w1=0,w2=1；当w≥0时，约定=1s，当<0w时约定=2s。

② 有理数的向量表示

③ 有理数的编码表示

根据②中的方式，可以将w表示成向量V(w)。若将V(w)的分量s,看作字母表{0,1,2,,9}…上的字符串，进一步应用连接运算得到一个长度为21k+的新的字符串，并记为W，显然W亦可看作一个正整数，称其为w的编码整数。例如，w1=2/3对应编码整数W1=123,w2=23对应编码整数W2=12301,w3=−0.048对应于编码整数W3=2006125。

（2）有理数编码方案的对应关系

设一个映射BM:Q→，其中Q为有理数集合，为编码整数集合（由集合Q中的有理数通过有理数编码方案得到的编码整数集合）。BM是一个双射，即有理数集合Q与编码整数集合是一一对应的。

综上所述，映射BM是双射，利用上述有理数编码方式得到的编码整数集合与有理数集合Q是一一对应的，即任一有理数存在唯一与之对应的编码整数。因此，两个有理数,xy相等当且仅当它们的编码整数相等。为叙述方便，下文中将这种编码方案简记为BMF。

2.2 有理向量的编码

（1）有理向量的编码方式

（2）有理向量编码方案的对应关系

根据上述有理向量的编码过程可知，有理向量的编码方案是以有理数编码方案BMF为基础的，类似于有理数编码方案的对应关系，当向量位数n确定时，按照上述有理向量编码方案得到的编码整数存在唯一与之对应的n维有理向量。n维有理向量和正整数形成一一对应关系，称为有理向量的编码整数，记该编码方案为VBMF。

下文中有理数组的编码方法与有理向量的编码方法类似，在此不再重复叙述。

3 相等问题的保密判定方案

本节主要应用单向哈希函数和上节所介绍的编码方案设计有理数相等问题（REq，rational number equality problem）以及有理向量相等问题（RVEq，rational number vector equality problem）的保密判定协议。本文涉及的随机数均为非零随机数。

3.1 有理数相等问题

问题描述Alice有一个有理数x，Bob有一个有理数y，他们想保密判定两个有理数是否相等，不泄露双方的任何信息。

基本思想按照前面所述的BMF编码方案，任意有理数w与一个编码整数W形成一一对应关系。如果有理数x,y对应的编码整数分别为X,Y，则，两个有理数相等的保密判定问题转化为两个整数相等的保密判定问题。

下面将结合编码方案BMF与单向哈希函数设计有理数相等问题的保密判定方案，为叙述方便，定义二元谓词。

具体协议如下。

协议1有理数相等保密判定协议

输入Alice输入有理数x，Bob输入有理数y

输出P(x,y)

准备Alice和Bob共同商定一个单向哈希函数Hash()

1) Alice和Bob分别随机选取足够大的有理数r和t，计算x1=x+r和y1=y+t，并将结果发送给对方。

2) Alice和Bob执行以下操作：

a) Alice计算y2=y1+r，Bob计算x2=x1+t；

b) 利用BMF编码方案，Alice和Bob分别把有理数y2和x2编码为十进制正整数Y2=BM(y2)和X2=BM(x2)；

c) Alice和Bob分别计算h1=Hash(Y2)和h2=Hash(X2)，并将结果发给对方。

3) Alice和Bob各自比较h1与h2。如果h1=h2，则输出P(x,y)=1；否则，输出P(x,y)=0。

协议1的正确性

证明。首先，由协议可知x2=x1+t=x+r+t,y2=y1+r=y+t+r。

根据BMF编码方案可知，X2与x2一一对应，Y2与y2一一对应，则。

协议1的安全性关于协议1的安全性，将从以下两部分分别进行详细的分析证明：① 安全性分析，包括理论分析和抵抗穷举攻击分析；② 安全性证明，对第①部分的理论证明。

安全性分析：根据协议1可知，Alice和Bob私有数据的安全性分析类似，故在此仅对Alice的私有数据进行安全性分析。

首先，在协议中Bob得到Alice发送的两个关系式

由于上面两个关系式含有两个未知数x和r，Bob只能设法从h1=Hash(BM(y+t+r))中解出r，再代入x1=x+r获得x；或Bob试图根据h1=Hash(BM(y+t+x1−x))直接求出x值。根据Hash函数性质，Bob想由h1=Hash(BM(y+t+r))求得r，或由h1=Hash(BM(y+t+x1−x))求得x，只能试图通过穷举攻击方法实现。而由于x,r均为Alice的私密有理数，即使x的范围限制在某有限区间内，由于有理数的稠密性，Bob不可能通过穷举攻击得到数据x的任何信息。因此，Alice的私有数据x是安全的。

安全性证明：通过前面的理论分析和抵抗穷举攻击的分析可知，协议1理论上是安全的。为了进一步证明协议1的安全性，通过严格的模拟范例方法进行证明，证明如下。

定理1有理数相等保密判定协议1是安全的。

证明在半诚实模型下，利用模拟范例方法严格证明协议1的安全性。构造模拟器S1(或S2)，使式(1)（或式(2)）成立。仅构造S2（S1的构造方法完全类似），对于输入(y,f2(x,y)=P(x,y))，模拟器S2按以下方式运行。

1)S2先任意选择x′，使P(x′,y)=P(x,y)。

2)S2选择随机数r′，并计算x1′=x′+r′。

3 )S2计算y2′=y1+r′和，并应用BMF编码方案将x2′,y2′分别编码为十进制正整数。

4)S2计算和。

由于r是Alice选的随机数，通过前面的安全性分析可知，Bob由x1=x+r,h1=Hash(BM⋅ (y+t+r))无法获得Alice数据x和r的任何信息，因此有

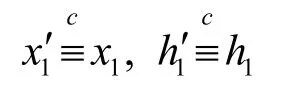
又由于P(x′,y)=P(x,y)，因此

类似地，可以构造模拟器S1使

证毕。

3.2 有理数相等问题−优化的REq协议

协议2有理数相等保密判定协议

输入Alice输入有理数x，Bob输入有理数y

输出P(x,y)

准备Alice和Bob共同商定一个单向哈希函数Hash()

1) Bob执行以下操作：

a) 随机选取足够大的有理数t，计算y1=y+t和y2=2y+t；

b) 利用BMF编码方案，把有理数y2编码为整数Y2=BM(y2)并计算h2=Hash(Y2)，将y1和h2发送给Alice。

2) Alice执行以下操作:

a) 计算x1=x+y1，并将有理数x1编码为整数X1=BM(x1)；

b) 计算h1=Hash(X1)，并比较h1与h2，如果h1=h2，则输出P(x,y)=1; 否则，输出P(x,y)=0。

分析协议2的正确性和安全性完全类似于协议1，故详细的分析在此省略。协议2只需要半轮通信，通信效率高于协议1，但降低了协议的公平性。因此，根据不同的场景，可以选择不同的协议进行计算。关于协议2的安全性有下面定理2。

定理2有理数相等保密判定协议2是安全的。 协议2的证明过程完全类似于协议1，故在此省略。

3.3 有理向量相等问题

问题描述Alice拥有有理向量(x1,…,xn)，Bob拥有有理向量（这里有理向量指向量的所有分量都是有理数），双方想要保密判定两个向量与是否相等。如果不相等，不应向对方泄露自己私密向量的任何信息。

计算原理根据有理向量的编码方法VBMF，分别将有理向量编码为正整数，则可将有理向量相等的保密判定问题转化为整数集上数值相等问题。

协议3有理向量相等保密判定协议

输入Alice输入有理向量，Bob输入有理向量

输出

1) Alice和Bob分别选取随机有理向量R=(r1,…,rn)和T=(t1,…,tn)（其中ri,ti(i∈[1,n])均为随机有理数），计算，并将结果发送给对方。

2) Alice和Bob执行如下步骤：

b) Alice和Bob根据向量编码方法VBMF分别将向量和编码为整数和；

协议3的正确性和安全性协议3的设计思想与协议1类似，协议3的正确性和安全性证明过程与协议1也相似，这里仅叙述下面定理。

定理3有理向量相等的保密判定协议3是安全的。

协议3的安全性证明完全类似于协议1，故在此省略。

4 集合问题的保密判定方案

本节主要以协议1和协议3的构造思想为基础，研究设计有理数域上元素与集合关系问题（ReES，the relationship problem between element and set）、坐标系中的点集合问题（RePS，point set problem of coordinate system）的保密计算协议。

4.1 元素与集合关系问题

问题描述Alice拥有私密的有理数集合X={x1,…,xn}，Bob拥有有理数y，他们希望合作保密判定y是否属于集合X，不泄露双方的任何信息（包括保密集合X的势）。

计算原理

1) 根据协议1的构造思想，Alice（或Bob）利用BMF编码对自己的有理数集合元素x1,…,xn（或y）进行编码，Alice得到编码整数集合U={u1,…,un}（其中ui=BM(xi),i∈[1,n]），Bob得到v=BM(y)。那么，判定y是否属于集合

X的问题可转化为判定v是否属于集合U的问题。

2) 为了隐藏Alice集合的势，Alice随机选择整数l>n，构造l−n个形如1b1…bk0…0或 2b1…bk0…0的“伪编码数”（这里k为任意选取的正整数，bj(j∈[1,k])在{0,…,9}中随机选取，最后k位设为零），记这些整数为un+1,…,ul。将这些整数添加到集合U中，得到一个势为l的新集合，将其记为。

3) 根据“伪编码数”un+1,…,ul的构造方式，由于任何有理数的编码整数都不可能是un+1,…,ul的形式，可知y∈X当且仅当v∈Uˆ。

下面根据上述计算原理设计协议，定义二元谓词P(y,X)：当y∈X时，P(y,X)=1；否则，P(y,X)=0。

协议4元素与集合关系的保密判定协议

输入Alice输入有理数集合X={x1,…,xn}，Bob输入有理数y

输出P(y,X)

1) Bob执行以下操作:

a) Bob随机选取足够大的有理数t，计算y1=y+t和y2=2y+t，并将y1发送给Alice；

b) Bob按照BMF编码方案，将y2编码为整数v=BM(y2)，并计算z=Hash(v)。

2) Alice执行以下操作：

a) Alice计算W={x1+y1,…,xn+y1}:={w1,…,wn}；

b) Alice按照BMF编码方案，将wi编码为整数ui=BM(wi)(i∈[1,n])，并随机添加“伪编码数”un+1,…,ul得到集合；

c) Alice计算Z={Hash(u1),…,Hash(ul)}:= {z1,…,zl}，并将Z发送给Bob。

3) Bob比较z与Z，若存在i∈[1,l]，使z=zi，则输出P(y,X)=1；否则，输出P(y,X)=0。

协议4的正确性根据协议4的过程和BMF编码方案可知

因此，协议4是正确的。

协议4的安全性关于协议4的安全性，从以下两部分进行详细的分析证明：① 安全性分析，包括理论分析和抵抗穷举攻击分析；② 安全性证明，对第①部分的理论证明。

安全性分析：首先分析Alice集合X的安全性。在协议执行中，Bob得到Alice发送的集合Z={z1,…,zl}。由于l是Alice选取的随机数，保证了Alice的集合势n的安全性，并且Bob无法区分出集合Z中的真假元素。根据单向哈希函数的性质，Bob无法从zi=Hash(ui)(i∈[1,l])中得到ui的任何信息，因此集合元素xi是安全的，集合X是安全的。

接着分析Bob数据y的安全性。Alice仅得到Bob发送的y1=y+t，由于Alice不知道随机数t，所以Bob的数据y是安全的。

下面说明协议4可以抵抗穷举攻击。协议4抵抗穷举攻击的过程和协议1类似，根据协议1的分析可知，由于有理数的稠密性，任意有理数的编码整数均匀分布在整个数轴上，所以编码整数的范围是无限的，故协议4可以抵抗穷举攻击。

安全性证明：通过前面的理论分析和抵抗穷举攻击的分析可知，协议4理论上是安全的。为了进一步证明协议4的安全性，通过严格的模拟范例方法进行证明，证明如下。

定理4元素与集合关系的保密判定协议4是安全的。

证明下面应用模拟范例严格证明定理4，为此需要构造模拟器S1（或S2），分别使式(1)（或式(2)）成立。

先构造S1。对输入(X,f1(y,X)=P(y,X))，S1按以下方式运行。 1)S1任意选择y′，使P(y′,X)=P(y,X)。

2)S1随机选取足够大的有理数t′计算y1′=y′+t′和y2′=2y′+t′。将y2′编码为整数v′=BM(y2′)，并计算h′=Hash(v′)。

3)S1计算。并将wi′编码为整数ui′ =BM(wi′)(i∈[1,n])。根据计算原理，S1随机添加“伪编码数”得到集合。

由于t和t′为随机数，有，因此；进一步，由于P(y′,X)=P(y,X)，因此。

对于输入(y,f2(y,X)=P(y,X))，模拟器S2按以下方式运行。

1)S2构造含n′个元素的集合， 使P(y,X′)=P(y,X)。

2)S2计算，并且按照BMF编码方案，将wi′编码为整数ui′ =BM(wi′)(i∈[1,n′])。由计算原理，S2随机添加“伪编码数”得到集合。

3)S2计算Z′={Hash(u1′),…,Hash(ul′ )}:= {z1′,…,zl′ }。

证毕。

4.2 坐标系中的点集合问题

目前，在SMC中对集合问题的研究仅限于元素为单一数据的集合。当集合元素是一个数组时（如集合元素是坐标点(x,y)），现有的解决方案并不适用。因此，本节研究坐标点集问题（进一步可以扩展到更高维的集合问题）。

问题描述Alice有一个点集合A={a1,…,an}，Bob有一点a0，其中ai=(xi,yi)且xi,yi(i∈[0,n])均为有理数。他们想保密判定是否a0∈A，不泄露双方的任何信息A,a0。

计算原理根据VBMF编码方案，Alice将点ai=(xi,yi)编码为整数，得到一个新的集合；Bob将点a0=(x0,y0)编码为整数。那么

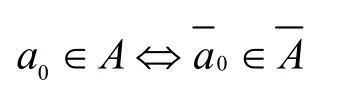
为方便叙述，定义P(a0,A)：若a0∈A，P(a0,A)=1；否则，P(a0,A)=0。协议5点与点集合关系的保密判定协议

输入Alice输入一个点集合A={a1,…,an}，Bob输入点a0=(x0,y0)

输出P(a0,A)

1) Bob随机选取点T=(t1,t2)计算，其中t1,t2均为有理数，并将发送给Alice。

2) Alice执行以下操作：

a) Alice随机选取点集合R={R1,…,Rn}计算W={a1+R1,…,an+Rn}:={w1,…,wn}以及，其中Ri=(ri1,ri2)，均为有理数。

b) Alice对点集合W和U执行相同的随机置换得到和。根据VBMF编码方案，Alice将点uˆi(i∈[1,n])编码为整数，并得到向量。

3) Bob执行以下操作：

c) Bob比较Z和Z′。若存在i∈[1,n]，使zi=zi′ ，则输出P(a0,A)=1；否则，输出P(a0,A)=0。

协议5的正确性根据协议5的过程以及VBMF编码方案可知

因此，协议5是安全的。

协议5的安全性关于协议5的安全性，本文从以下两部分分别进行详细的分析证明：① 安全性分析，包括理论分析和抵抗穷举攻击分析；② 安全性证明，对第①部分的理论证明。

安全性分析：下面分析协议5的安全性，并表明协议5可以抵抗穷举攻击。首先，分析Alice集合A的安全性。在协议执行中，Bob得到Alice发送的Z=(z1,…,zl)和。根据单向哈希函数的性质可知，Bob根据zi=Hash(ui)(i∈[1,n])得不到关于ui或者Ri的任何信息。进一步，对于中的有理数组ai和Ri均为Alice的私有数据，因此Bob根据得不到关于ai的任何信息，即点ai是安全的。因此集合A是安全的。

其次，分析Bob的点a0的安全性。Alice仅得到Bob发送的，因为随机数组T是Bob的私密数据，Alice根据得不到a0的任何信息。因此，Bob的点a0是安全的。

最后，说明协议5可以抵抗穷举攻击。协议5抵抗穷举攻击的过程类似于协议1和协议4，故在此省略。

安全性证明：通过前面的理论分析和抵抗穷举攻击的分析可知，协议5理论上是安全的。为了进一步证明协议5的安全性，下面通过严格的模拟范例方法进行证明。

定理5点与点集合关系的保密判定协议5是安全的。

协议5的安全性证明过程完全类似于协议4，故在此省略。

5 性能分析

下面对本文所设计协议的性能和适用范围进行分析，并与现有相关协议分析进行比较。文献[17,18]分别研究了整数范围和有理数域上的数据相等问题，主要以Hash函数以及Paillier同态加密算法为基础设计协议，文献[17]的协议计算效率较高但仅适用于整数范围；文献[18]解决了有理数相等问题但计算效率相对较低。文献[21]以Paillier同态加密算法为基础设计了有理数域上元素与集合关系的保密判定协议，但计算效率低且应用范围小。

下面主要通过比较各协议所需要进行的Hash运算次数以及模指数运算的次数来衡量计算复杂性，而应用执行协议所需要的通信轮数来衡量协议的通信复杂性。为了便于分析比较，假设Alice集合的势为n，Bob集合的势为m。

5.1 理论分析与比较

5.1.1 计算复杂性分析

本文协议1～协议5主要运用了基本算术运算（普通实数的加减乘除运算）和Hash运算，由于基本算术运算与Hash运算相比计算复杂性可以忽略，在此只考虑Hash运算次数。

协议1（协议2）中Alice和Bob分别执行了1次Hash运算，因此协议1（协议2）共执行了2次Hash运算。协议3应用协议1的基本思想，将向量相等问题转化为数值相等问题，协议3也需要执行2次Hash运算。协议4中Alice执行了l次Hash运算，Bob执行了1次Hash运算，即协议4共执行了l+1次Hash运算（其中l是为隐藏集合X的势选取的大于|X|=n的一个数值，不需要取值太大，能够保证协议4具有线性复杂性）。基于协议4的设计思想，协议5首次解决了坐标系中点与点集合关系的保密计算问题。在协议5中，Alice和Bob均需要执行n次Hash运算，即协议5共执行了2n次Hash运算。

文献[17]基于Hash函数设计了正整数范围内相等问题的保密判定协议1和向量相等协议2，协议1和协议2均需执行2次Hash运算。文献[18]基于Paillier同态加密算法设计了有理数相等保密判定协议，协议共需要6次模指数运算。文献[21]基于Paillier同态加密算法设计了有理数域上元素与集合关系的保密判定协议，其中Alice需要执行l+2次模指数运算，Bob需要执行2l+6次模指数运算，协议共需执行3l+8次模指数运算。

5.1.2 通信复杂性分析

本文协议1和协议3各需要2轮通信；协议2需要半轮通信；协议4～协议5各需要1轮通信。

文献[17]中的协议1和协议2均需2轮通信；文献[18]需要2轮通信；文献[21]需要2轮通信。

根据上述理论分析，现将本文协议的效率及适用范围分析的结果在表1中给出。在表1中，其中计算功能一栏为所列文献研究的具体内容；计算复杂性一栏，H（或M）表示Hash（或模指数）运算，通信复杂性为通信轮数。

表1 协议的效率分析与适用范围比较Table 1 Efficiency analysis and scope analysis of the protocols

通过表1分析可知，本文协议仅需较少的Hash运算即可实现有理数（或有理向量）相等问题以及有理集合问题的保密判定，扩展了相关安全多方计算问题的适用范围且计算效率优势明显。

5.2 实验测试

表1从理论上对本文协议和以往相关协议的效率进行了全面分析，并进行了比较。下面进一步利用Java编程语言在MyEclipse上对本文协议4和文献[21]的协议进行编程实现。

（1）实验平台

计算机的配置如下：操作系统为Windows10企业版，Intel Core i5-6600 CPU @3.30 GHz，安装内存8.00 GB，64位操作系统。在此，约定本文协议所做模拟实验均在此环境下进行。

（2）实验结果

本文协议4应用单向哈希函数，文献[21]应用Paillier同态加密体制，下面分别对本文协议4和文献[21]进行仿真实验。实验设定Paillier加密方案中大素数p和q的位数为512 bit，因此模数的位数为1 024 bit。保密数据的范围为[−100, 100]。通过对本文协议4和文献[21]的协议进行实际计算，对每种协议进行多次实验，实验结果随机抽取50次数据求取平均值，结果如表2所示。

表2 实验结果分析Table 2 Analysis of simulation result

由表2可知，与文献[21]相比，本文协议4的计算效率较高，且优势明显。理论分析（表1）和实验测试（表2）两方面均表明本文协议优势明显。

为了进一步测试效率和集合基数（添加“伪编码”数后的元素个数）之间的关系，对本文协议4和文献[21]分别进行了多维实验测试，实验结果如图1所示。

在不同基数下的仿真结果（图1）表明本文协议4的计算效率随集合基数的变化幅度较小，文献[21]的计算效率随集合基数的变化幅度较大，本文协议4具有明显优势，且本文协议4更适用于集合基数大的应用场景，适用范围更广。

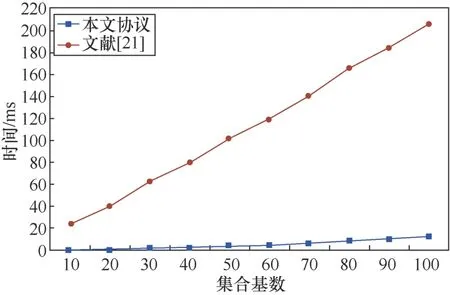
图1 计算效率与集合基数的关系Figure 1 The relationship between computational efficiency and set cardinality

6 协议的推广及实际应用

目前关于有理数域上的安全多方计算的研究较少，但在计算几何等方面有理数的应用十分广泛，下面根据前面协议的设计思想，对更广泛的有理数域上安全多方计算实际应用问题设计新的高效的保密协议。

直线位置关系问题描述

Alice有一条直线l1:y=k1x+b1，Bob有一条直线l2:y=k2x+b2，双方要保密判定两条直线的位置关系（重合、平行、相交、垂直），不泄露各自的私密信息。

直线位置关系计算原理

首先，根据两条直线位置关系的判定定理可知，① 当两条直线的斜率k1=k2且截距b1=b2时，两直线重合，记为l1=l2；② 当两条直线的斜率k1=k2但截距b1≠b2时，两直线平行，记为l1‖l2；③ 当两条直线的斜率k1≠k2时，两直线相交，记为l1×l2；④ 当两条直线的斜率满足k1×k2=−1时，两直线垂直，记为l1⊥l2。特别地，当直线与X轴平行时，记直线斜率为−0/1； 当直线与Y轴平行时，记直线斜率为1/0。那么，两直线位置关系描述如下。

其次，Alice和Bob利用有理向量的编码方法VBMF，将向量(k1,b1),(k2,b2)分别编码为整数u1,v1；Alice利用有理数编码方法BMF，将斜率k1,−1/k1分别编码为整数u2,u3；Bob利用有理数编码方法BMF，将斜率k2编码为整数v2，则

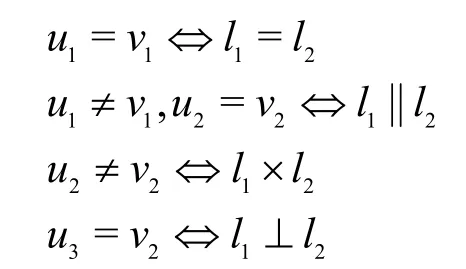
根据上述计算原理设计协议，为叙述方便，定义二元谓词P(l1,l2)如下。

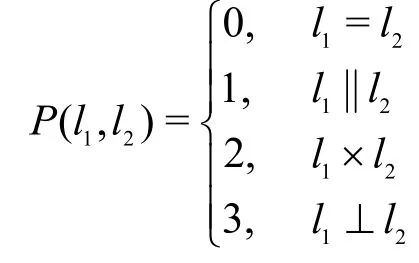
具体协议如下。

协议6直线位置关系的保密判定协议

输入Alice输入直线l1:y=k1x+b1，Bob输入直线l2:y=k2x+b2

输出P(l1,l2)

准备Alice、Bob商定单向哈希函数Hash()

1) 按照计算原理所述，Alice利用VBMF编码方案和BMF编码方案，将向量(k1,b1)以及分别编码为整数u1,u2,u3；类似地，Bob利用VBMF编码方案和BMF编码方案，将向量(k2,b2)以及k2分别编码为整数v1,v2。

2) Bob选取充分大的随机数t1,t2（均为有理数），分别计算和，并将结果发送给Alice。

3) Alice选取充分大的随机数r1,r2,r3（均为有理数），计算W=(u1+r1,u2+r2,u3+r3):=(w1,w2,w3)，以及(z1,z2,z3)，并将W,Z发送给Bob。

Bob比较Z与Z′的各个分量，如果z1=z1′，则输出P(l1,l2)=0；如果z1≠z1′,z2=z′2，则输出P(l1,l2)=1；如果z2≠z2′，则输出P(l1,l2)=2；如果z3=z3′，则输出P(l1,l2)=3。

协议6的正确性和安全性协议6的设计思想本质上是协议1和协议3设计思想的推广。根据协议1和协议3的正确性和安全性可知，协议6是正确且安全的。

7 结束语

本文提出了有理数域上一些基本的安全多方计算问题，设计了有理数（数组）的编码方法，并以此为基础解决了有理数域上相等问题和集合问题的保密计算。通过对本文协议进行适当的应用，可以进一步解决有理数域上其他的安全多方计算问题，对后续有理数域上安全多方计算问题的研究和应用具有重要意义。目前，本文的协议是在半诚实模型下设计的，未来将进一步研究恶意模型下有理数域上的安全多方计算问题。