基于三点拉格朗日数字滤波器的响应谱优化分析

徐飞，高兵兵

(1.盐城工学院 汽车工程学院，江苏 盐城 224051；2.西北工业大学 自动化学院，陕西 西安 710072)

火炮作为地面部队装备的主要火力武器，其结构设计越来越复杂，使用环境也趋于恶劣，其使用可靠性问题已经成为影响作战效能发挥的主要因素。因此,如何评估和提高火炮的可靠性成为目前亟需解决的问题。响应谱和疲劳损伤等效技术被广泛用于制定振动加速试验谱[1-2]，进而评估武器装备系统(尤其是火炮、战车等)在振动环境下的潜在损伤和疲劳寿命[3]。为提高响应谱计算效率和精度，Kelly和Smallwood分别提出采用脉冲响应不变数字滤波器和斜阶跃响应不变数字滤波器计算冲击响应谱(Shock Response Spectrum, SRS)[4-5]。Ahlin对Smallwood的算法进行了改进，给出了利用斜阶跃响应不变法计算SRS和疲劳损伤谱(Fatigue Damage Spectrum, FDS)的MATLAB程序[6]。Brandt等对比了脉冲响应不变法、斜阶跃响应不变法和Runge-Kutta方法在单自由度和多自由度系统中的计算结果，指出数字滤波器在计算速度、解的稳定性、动力学范围以及误差的可控性方面都明显优于Runge-Kutta[7]。ISO 18431-4给出了利用斜阶跃响应不变法计算SRS的具体过程，并分析了该方法引入的偏置误差[8]。Ahlin等[9]分析了脉冲响应不变法引入的混叠误差以及阶跃响应不变法引入的偏置误差和相位误差，并给出了利用斜阶跃响应不变法计算非线性力学系统强迫响应的方法[10-11]。近年来，利用斜阶跃响应不变法计算SRS、极值响应谱(Extreme Response Spectrum, ERS)和FDS，以评估振动与冲击环境及推导试验谱等已得到了广泛的关注和应用[12-14]。

尽管现有斜阶跃响应不变法引入的误差随着采样频率的增大而减小，但即使采样频率大于激励信号最高频率10倍以上，其误差依然较大。为进一步减小误差，笔者基于卷积核重点研究了三点拉格朗日法引入的响应偏置误差和相位误差，并在不同采样率下与斜阶跃响应不变法进行了对比，最后基于三点拉格朗日数字滤波器对FDS和ERS进行了优化分析，并结合案例对上述过程进行了阐述。

1 理论建模

1.1 基于数字滤波器的FDS和ERS数学模型

对于时域信号，线性时不变力学系统的响应等于激励信号与脉冲响应信号的卷积：

(1)

式中：x(t)为响应；f(τ)为激励；h(t)为脉冲响应信号。

对于离散信号，当前时间步的系统响应x(n)可表示成如下数字滤波器形式[9]：

(2)

式中：bj和aj为数字滤波器系数；Nb和Na为数字滤波器阶数。

考虑一个Q输入P输出的多自由度线性力学系统，其系统传递函数可表示为模态模型：

(3)

式中：Nm为模态阶数；[Rr]P×Q和Pr分别为系统第r阶模态的留数矩阵和极点；上标*表示复共轭。

由式(2)和(3)可知，利用数字滤波器可将多自由度系统在q点输入下p点的响应表示为

(4)

因此，构造出不同数字滤波器的系数即可求解多自由度系统在任意激励下的响应。笔者重点研究斜阶跃响应不变法以及三点拉格朗日法两种数字滤波器。

常见的振动响应谱包括FDS和ERS。FDS本质上描述了一系列单自由度系统对同一个加速度激励的响应，如图1所示的各个单自由度系统的响应被转换成一定时间内的疲劳损伤并与其共振频率形成一一对应关系，如图2所示。

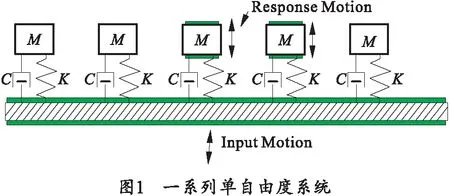
在输入加速度x(t)下，一个共振频率为fn，阻尼比为ζ的单自由度系统的加速度输出xa可利用数字滤波器求解：

xa=filter(b,a,x(t)),

(5)

式中：a和b对应式(4)中所采用的数字滤波器的系数；filter为MATLAB函数。

在时域计算FDS时，利用雨流计数法对各应力水平下的循环次数进行计数，然后结合S-N曲线和Miner准则计算疲劳损伤量：

(6)

(7)

式中：Ni为应力Si下的疲劳寿命；b为疲劳指数；D为时域总损伤；p为所考虑的应力量级数；ni表示在应力Si下的循环次数。

假设应力与加速度成正比：

S=kxa，

(8)

则式(7)可表示为

(9)

ERS和FDS类似，不同之处在于ERS表示的是各单自由度系统的最大响应值与其共振频率之间的对应关系，即

DERSt=max(filter(b,a,x(t))).

(10)

由式(9)、(10)可以看出，相比ERS，FDS由于受疲劳指数b(通常大于1)的影响，对不同数字滤波器的算法更加敏感，进一步验证见2.2节。

1.2 数字滤波器误差分析

各种数字滤波器方法对于输入信号在单位采样时间内的插值近似都可看成是时域激励信号与各滤波器卷积核的卷积，该卷积对应于频域的乘积。斜阶跃响应不变法的卷积核及其傅里叶变换如下[9]：

(11)

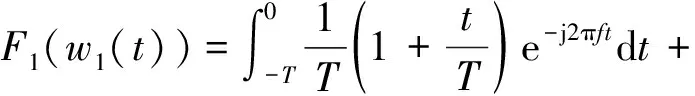
(12)

三点拉格朗日法的卷积核及其傅里叶变换如下：

(13)

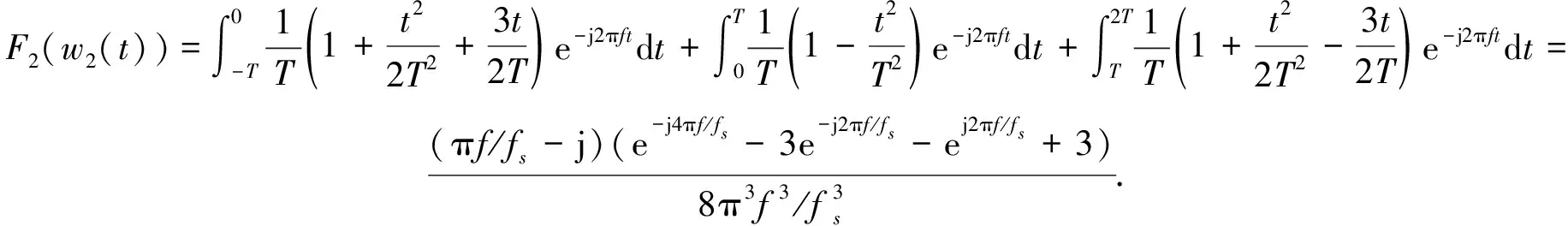
(14)

由式(11)～(14)可以看出，数字滤波器引入的偏置误差(%)和相位误差分别为

(15)

(16)

2 仿真案例

2.1 基于数字滤波器的响应误差对比

以单自由度系统为例，详细对比斜阶跃响应不变法以及三点拉格朗日法引入的偏置误差和相位误差。系统参数如下：m=1 kg，c=6 N·s/m，k=10 kN/m，采样频率fs=80 Hz。

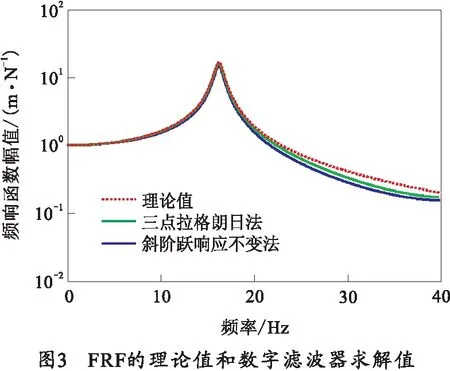
在单位脉冲激励下，图3对比了理论FRF和采用数字滤波器方法得到的FRF。从图3可以看出，两种数字滤波器法得到的FRF都偏离了理论值。偏置误差随着信号最高频率f和采样率fs之比的增大而增大，如图4所示。

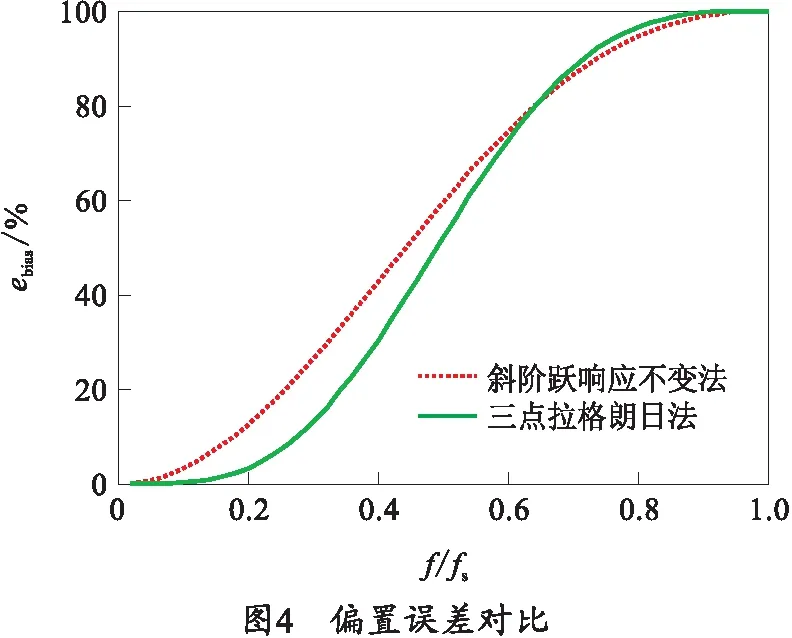
从图4可以看出，当频率比低于0.1时(即采样频率fs大于信号最高频率f的10倍以上时)，偏置误差均小于5%，其中三点拉格朗日法偏置误差更小并接近0。

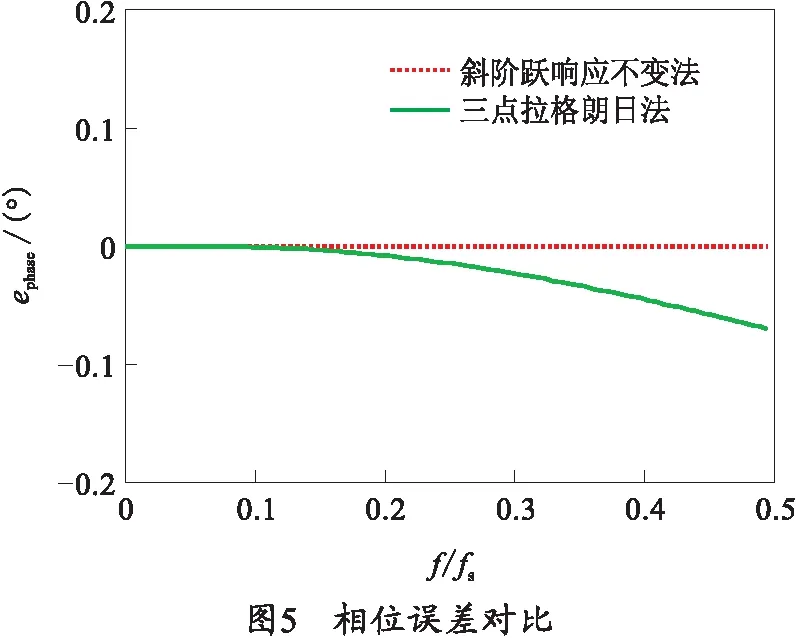
图5给出了两种数字滤波器方法引入的相位误差。从图5可以看出，斜阶跃响应不变法相位误差为0，三点拉格朗日法的相位误差随着信号最高频率和采样率之比的增大而增大，当频率比低于0.1时(即采样频率fs大于信号最高频率f的10倍以上时)，三点拉格朗日法的相位误差接近0。

2.2 基于数字滤波器的响应谱优化分析

假设激励加速度为xa(t)，持续时间为60 s，对应频率范围2～40 Hz，功率谱密度为0.01 g2/Hz，如图6所示。令质量因子Q=10，疲劳指数b=4，分别基于斜阶跃响应不变法和三点拉格朗日法计算位移FDS和ERS。为对比不同采样频率下两种滤波器计算结果，令采样频率分别为激励信号最大频率的2、4、6、10倍，结果如图7、8所示。

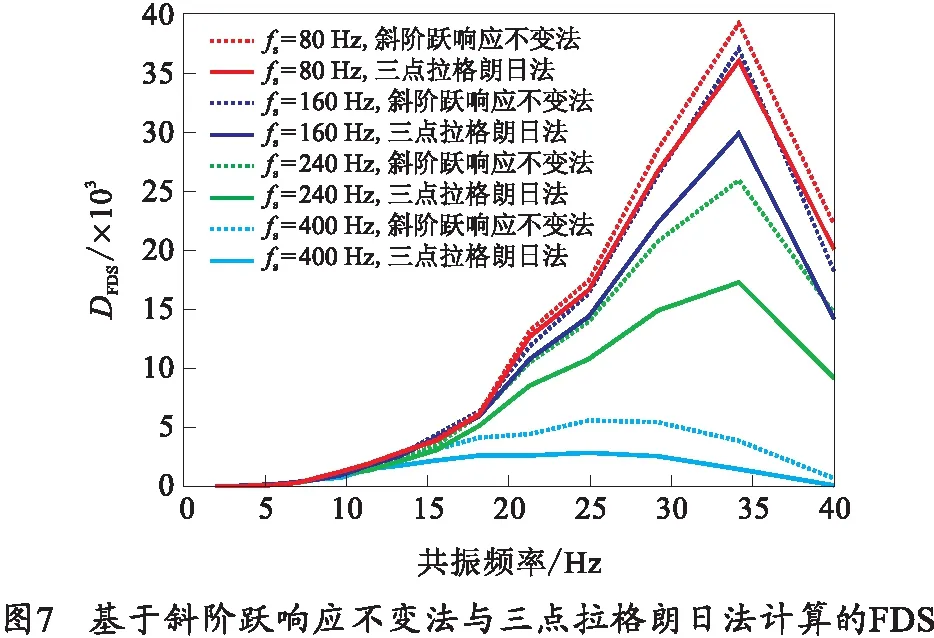
从图7、8可以看出，采样频率越大，利用两种数字滤波器方法得到的FDS和ERS越准确，且得到的FDS和ERS越接近；在同样的采样率下，利用三点拉格朗日法得到的FDS和ERS更准确；由于最大共振频率与加速度激励的最高频率重合，因此在40 Hz附近两种滤波器算法下的FDS和ERS误差略有缩小；即使采样频率达到10倍的激励信号最大频率，利用三点拉格朗日法得到的FDS和ERS依然比斜阶跃响应不变法更准确。

利用三点拉格朗日法和斜阶跃响应不变法计算FDS和ERS，在不同频率点计算得到两种方法的相对误差最大值，如图9所示。图中红色曲线是分别利用三点拉格朗日法和斜阶跃响应不变法计算得到的FDS的相对误差；绿色曲线是分别利用三点拉格朗日法和斜阶跃响应不变法计算得到的ERS的相对误差。

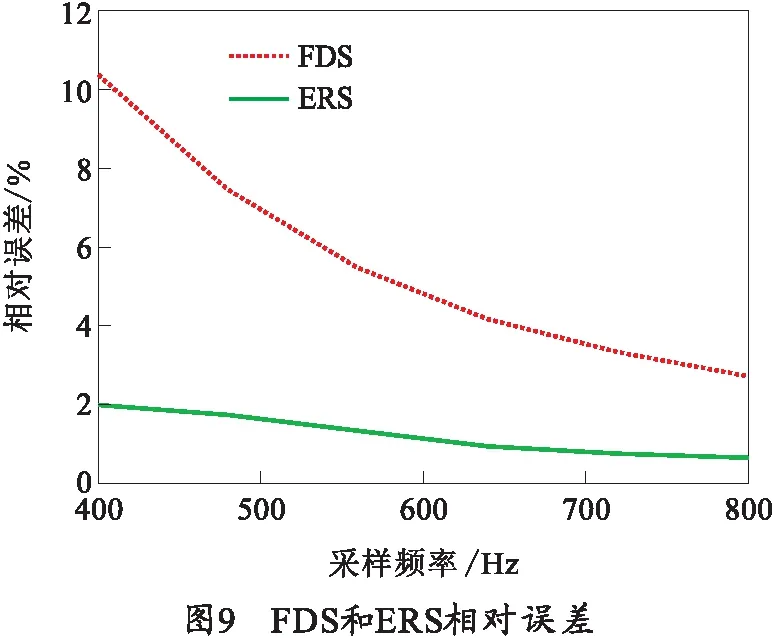
从图9可以看出，随着采样频率的增大，利用两种滤波器得到的FDS和ERS相对误差减小；当采样频率为激励最高频率的10倍时，FDS相对误差超过10%，ERS相对误差在2%到3%之间；当采样频率约为激励最高频率的15倍时，FDS相对误差小于5%；ERS相对误差明显小于FDS误差。

3 工程应用

GJB 150.16A—2009军用装备实验室环境试验方法规定，在随机载荷作用下，采用功率谱密度(Power Spectrum Density, PSD)评估振动环境下武器装备系统的振动耐久性[15]。然而，当实测载荷服从非高斯分布时，直接计算其PSD将引入较大误差。图10为实测非高斯随机载荷。

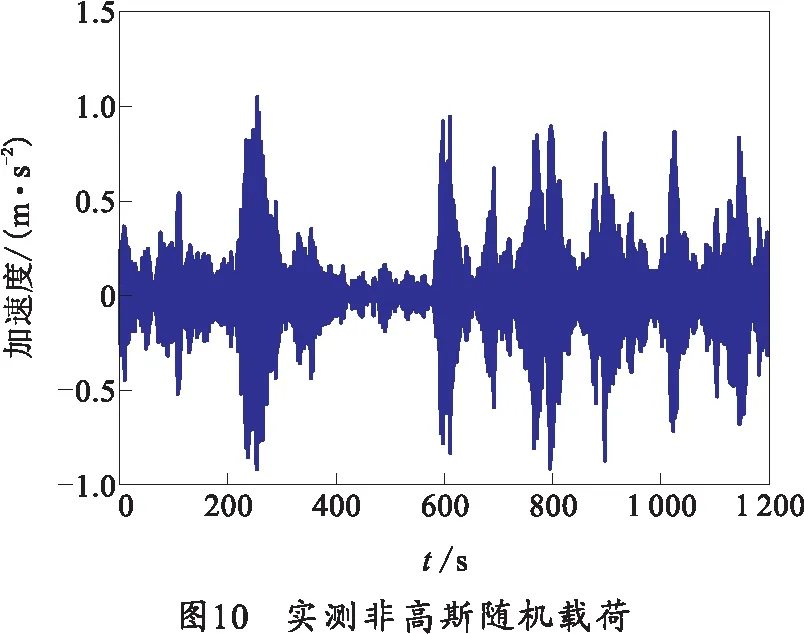
实测随机载荷的PSD如图11所示。利用该PSD可在频域直接求解FDS，如图12红色曲线所示，其隐含的假设是实测随机载荷服从高斯分布；而利用笔者给出的三点拉格朗日法可在时域求解实测随机载荷的FDS，可充分考虑实测载荷的非高斯随机特性，如图12蓝色曲线所示。

从图12可以看出，直接计算实测载荷的PSD会导致在整个频率段上明显的欠试验，从而降低武器装备系统的振动耐久性评估精度。

4 结论

笔者详细对比了斜阶跃响应不变法和三点拉格朗日法两种数字滤波器引入的偏置误差及相位误差，并基于三点拉格朗日数字滤波器对FDS和ERS进行了优化分析。结论如下：

1)采样频率大于激励信号的最高频率10倍以上时，两种数字滤波器的偏置误差均小于5%，其中三点拉格朗日法偏置误差更小且接近0。

2)当采样频率大于激励最高频率的10倍以上时，两种数字滤波器的相位误差均等于或接近0。

3)即使采样频率大于激励信号最高频率10倍以上，相比斜阶跃响应不变法，利用三点拉格朗日法计算得到的FDS和ERS依然更加准确，且FDS精度提高10%以上。

4)相比ERS，FDS对于所选用的数字滤波器方法更加敏感。

5)当实测随机载荷服从非高斯分布时，利用笔者给出的三点拉格朗日数字滤波器法计算时域FDS，进而反推损伤等效的PSD，可避免欠试验，提高振动疲劳寿命的评估精度。

综上所述，三点拉格朗日法引入的误差最小，应该取代斜阶跃响应不变法用于响应谱计算，其对于提高武器装备系统可靠性和疲劳寿命的评估精度具有重要的工程应用价值。