基于迁移成分分析和词包模型的变工况轴承诊断方法
2022-06-24田威威陈俊杰林意
田威威,陈俊杰,林意
(1. 江南大学 人工智能与计算机学院, 江苏 无锡 214122;2. 西门子中国研究院, 北京 100000)
在工业生产中,轴承是旋转机械的关键部件,由于长期连续工作在高载荷和高转速下,轻则会影响工厂企业的正常运作,重则会造成重大的经济损失,甚至出现毁机事故和人员伤亡。因此在早期有效地诊断轴承是否有故障具有十分重要的意义[1]。
运用传统的机器学习方法进行故障诊断[2-4]需要大量的带标签样本以训练分类器。而在实际生产中,轴承运行所产生的实时振动数据本身并无标签。同时,由于轴承种类繁多且工况复杂(如转速、温度及其他工作环境的变化),数据的分布差异巨大,因此已有的带标签样本并不一定适用于新近产生的数据,以此训练出的分类器更是难以满足需求。
为达到减小数据分布差异的目的,考虑使用迁移成分分析(TCA),其在故障诊断领域已有不少应用[5-6]。TCA由Pan等[7-8]提出,该算法将最大均值差异(MMD)[9]与主成分分析(PCA)[10-11]相结合,在领域之间寻找一种共享的特征表示,试图在减少数据分布差异的同时保持原始数据的内部属性。经过这种处理后的数据可以直接利用传统分类器对数据进行跨工况的训练和泛化。
在传统的TCA轴承故障诊断方法中,通过处理反应轴承状态信息的振动信号可以从中提取出轴承的特征,以便对轴承的状态进行分析从而判断轴承是否出现了故障,出现了何种故障。传统的方法从时域、频域及时频域3个方面进行特征提取。然而在实际现场中,信号干扰或者生产环境等因素会弱化轴承振动信号的规律性,使得在频谱上难以准确看到相应分布特征。当采用词包模型时,把每一时间帧下能量在频率维度上的分布看成一个单词,则每段信号就表示成了由各个单词组成的一篇篇文档,这就可以直接从数据的角度去揭示能量分布的这种规律性。
在此基础上,笔者提出一种基于迁移成分分析和词包模型的诊断算法,通过迁移成分分析将源域频谱数据(有标签)和目标域频谱数据(无标签)映射到同一分布下,对迁移后的数据建立词包模型,以词包的形式表示各个样本,以此为特征训练出相应分类器对轴承进行诊断。实验结果表明,该方法能够将已标记的数据用于训练分类器对新近产生的轴承数据进行分类,以达到故障诊断的目的。使用该方法,运用一种工况下的轴承数据作训练对另一工况下的轴承进行诊断具有显著的成效。
1 迁移词包模型
1.1 迁移成分分析
TCA是一种迁移学习方法,所谓迁移学习,即把已训练好的模型(源域)迁移到新的模型(目标域)来帮助新模型训练。在滚动轴承领域,由于轴承之间具有相似性,所以它们的振动数据之间应当具有可迁移性。
和主成分分析(PCA)方法一样,迁移成分分析本质上是一种降维算法,而TCA在拉近数据分布距离上更有优势。
1.2 词包模型
早期的词包模型(BOW)主要用于解决文本分析问题,如分析文档集、文档和单词三者间的相互关系。陈俊杰等[12]创造性地将其运用于轴承特征提取,并在基于该提取方式的轴承故障诊断中取得了极佳的效果。
其主要思想为对轴承振动信号进行短时傅里叶变换后得到频谱,将每个频谱片段视为一个单词,可以表示为1组V维的向量w=(0,…,1,…,0),其中wv=0,wu=1(v≠u)。
每个频谱可以由N个频谱片段组成,相当于由单词组成文档,即w=(w1,…wn,…,wN),其中wn是第n个频谱片段。
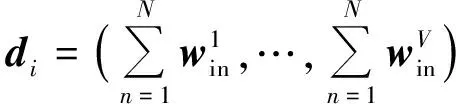
每个频谱中的单个频谱片段也可表示为wi=(wi1,wi2,…,wiV),从而可以将频谱表示为w=(w1,w2,…,wV),成为词包模型,整个频谱集合的词包模型如下:
(1)
1.3 模型建立
词包模型本质上是将特征以文本表示,虽然可以作为轴承的特征,但是由于每1维度之间并不具有相同的映射关系,所以失去了可迁移性。为了达到变工况轴承故障诊断的目的,考虑在词包模型完全建立之前进行迁移。此时,特征的表示形式为频谱能量分布矩阵,能量分布矩阵由多个分布片段组成。该矩阵由振动信号经短时傅里叶变换得到,每个分布片段之间完整地保留了相应的映射关系,在这样的情况下进行迁移成分分析可以更好地将该工况的能量分布矩阵迁移到另一工况的数据分布下。
源域频谱能量分布矩阵经过迁移后,其数据分布已更接近于目标域工况下轴承的能量分布矩阵,因而使用在其基础上训练的分类器对目标域工况下的轴承进行诊断可以取得良好的效果。
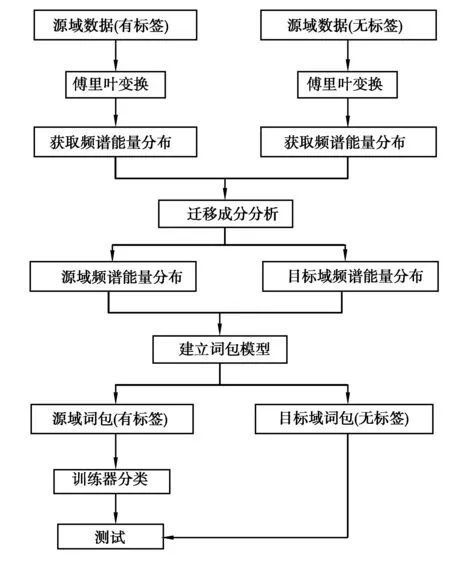
迁移词包模型建立流程如图1所示。
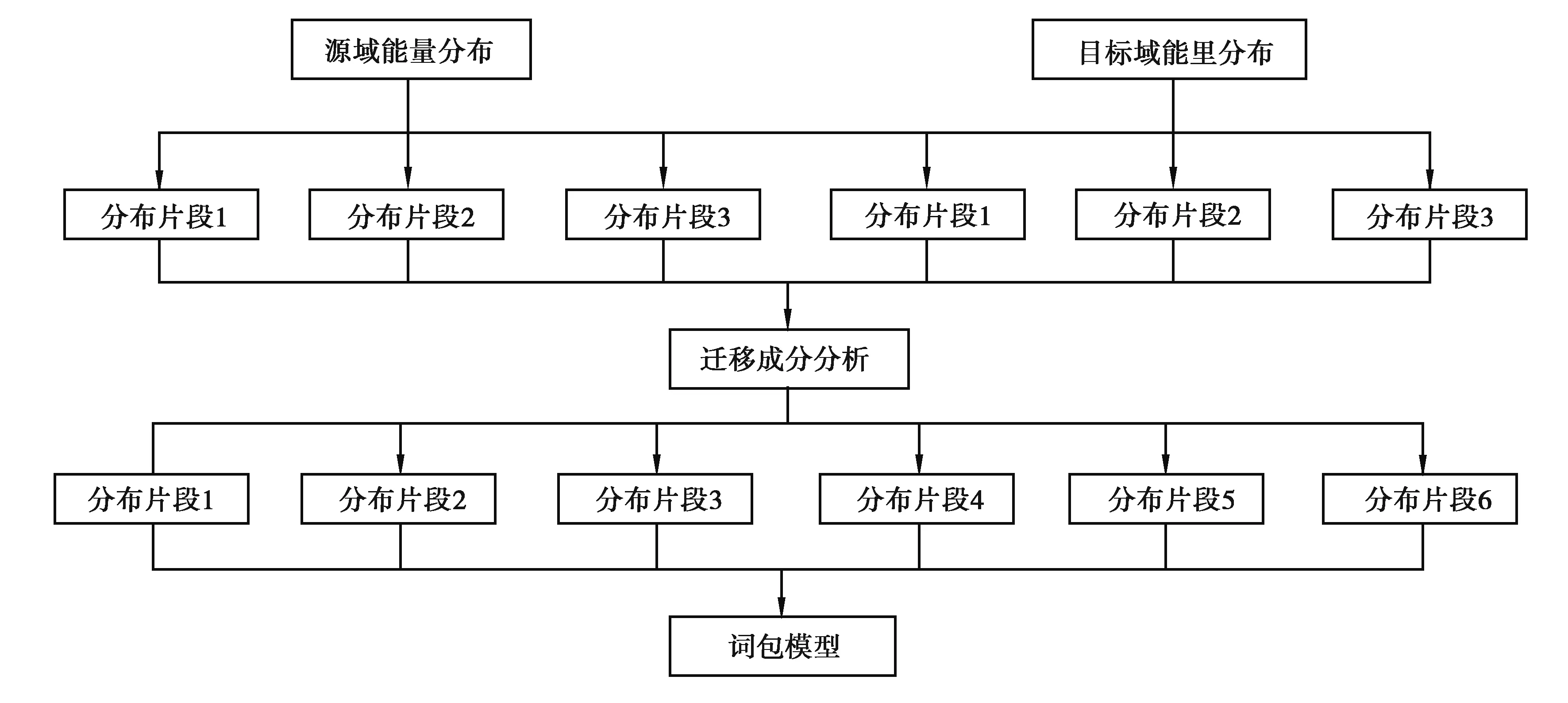
图1 迁移词包模型建立流程Fig. 1 TCA-BOW model establishment process
2 基于迁移词包模型的轴承故障诊断
2.1 特征提取
对轴承进行诊断,首先要根据轴承的振动信号提取特征。通过对振动信号进行短时傅里叶变换获取其能量分布并建立相应的词包模型是一种有效的特征提取方式。
2.1.1 能量分布
短时傅里叶变换(STFT)[13]是一种线性时频变换,定义为
(2)
式中:t为时间;f为频率;x为源信号;γ为窗函数,可视为某段信号在某段时间内的局部频谱。
P(m,n)=|T(m,n)|2。
(3)
图2为轴承4种不同状态下其振动信号的能量分布。

图2 各状态下的能量分布Fig. 2 Energy distribution in each state
功率谱密度(PSD)的分布矩阵MP如式(4)所示,其中Nt,Nf分别是时域和频域的片段数目。
(4)
2.1.2 迁移成分分析
对源域信号及目标域信号进行短时傅里叶变换可以得到两者的PSD。但此时这些PSD 并不处于同一分布,源域与目标域距离过大,据此建立的词包模型难以准确地描述轴承的故障情况。分布情况如图3所示,其中红色为源域,蓝色为目标域。
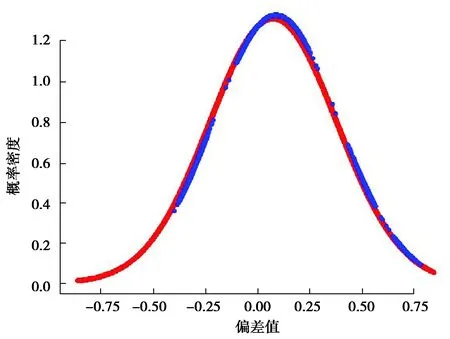
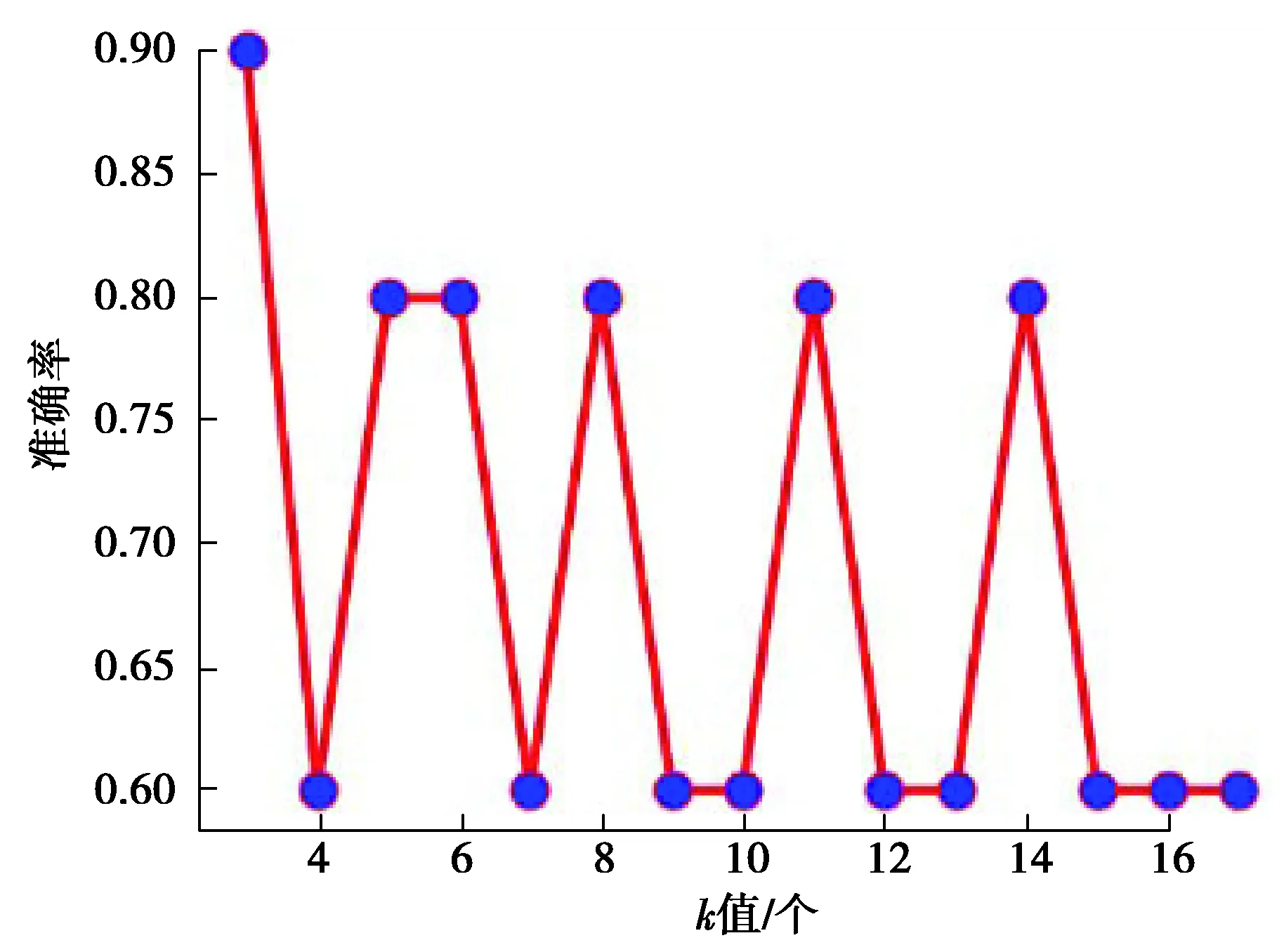
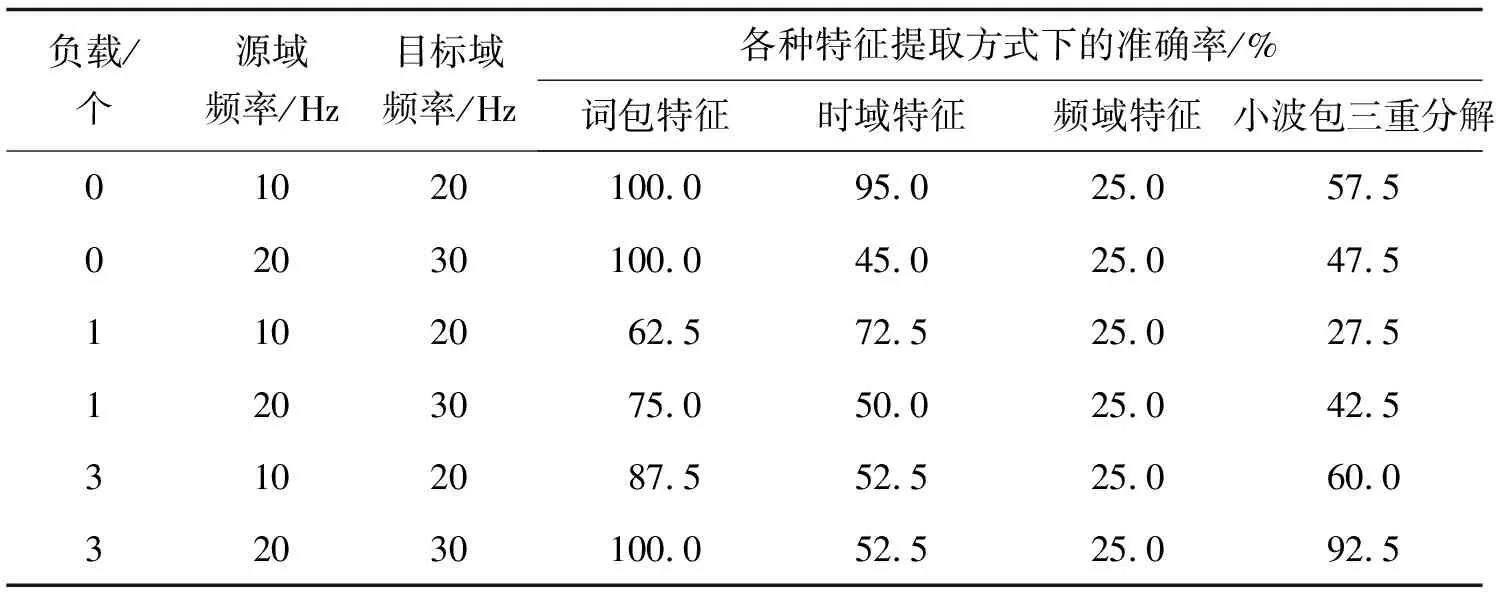
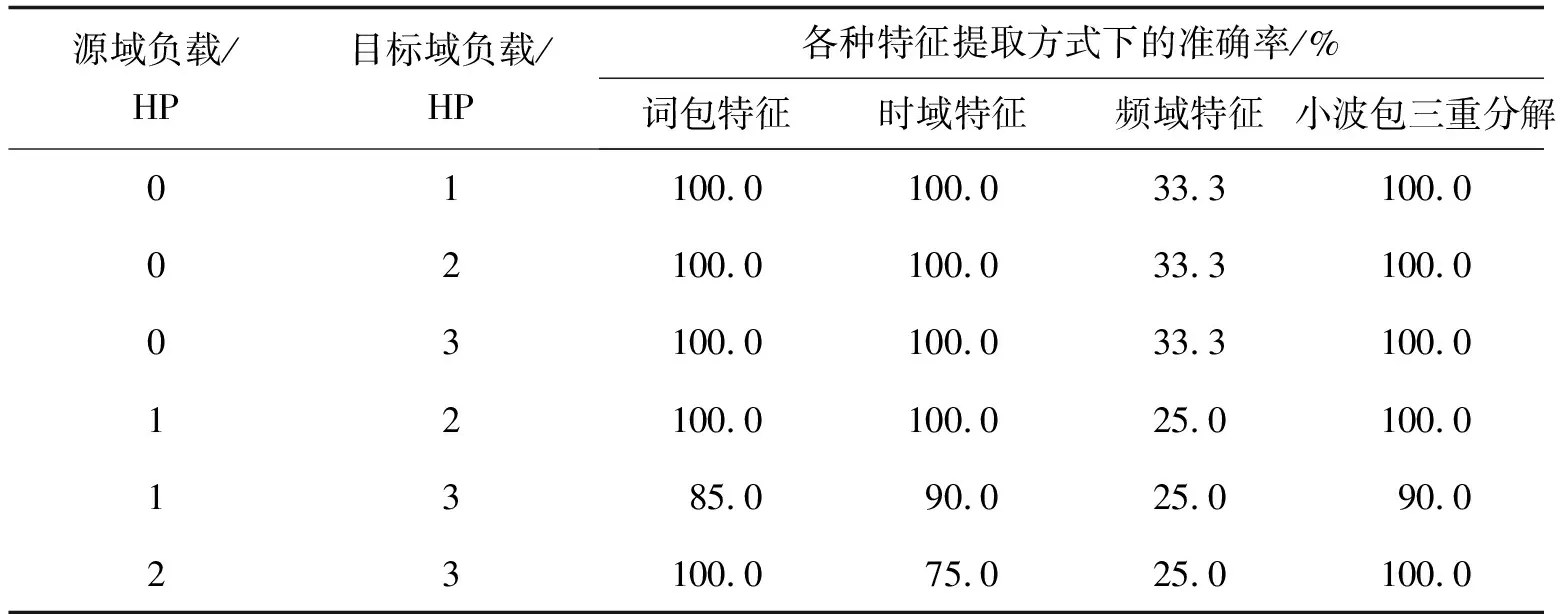
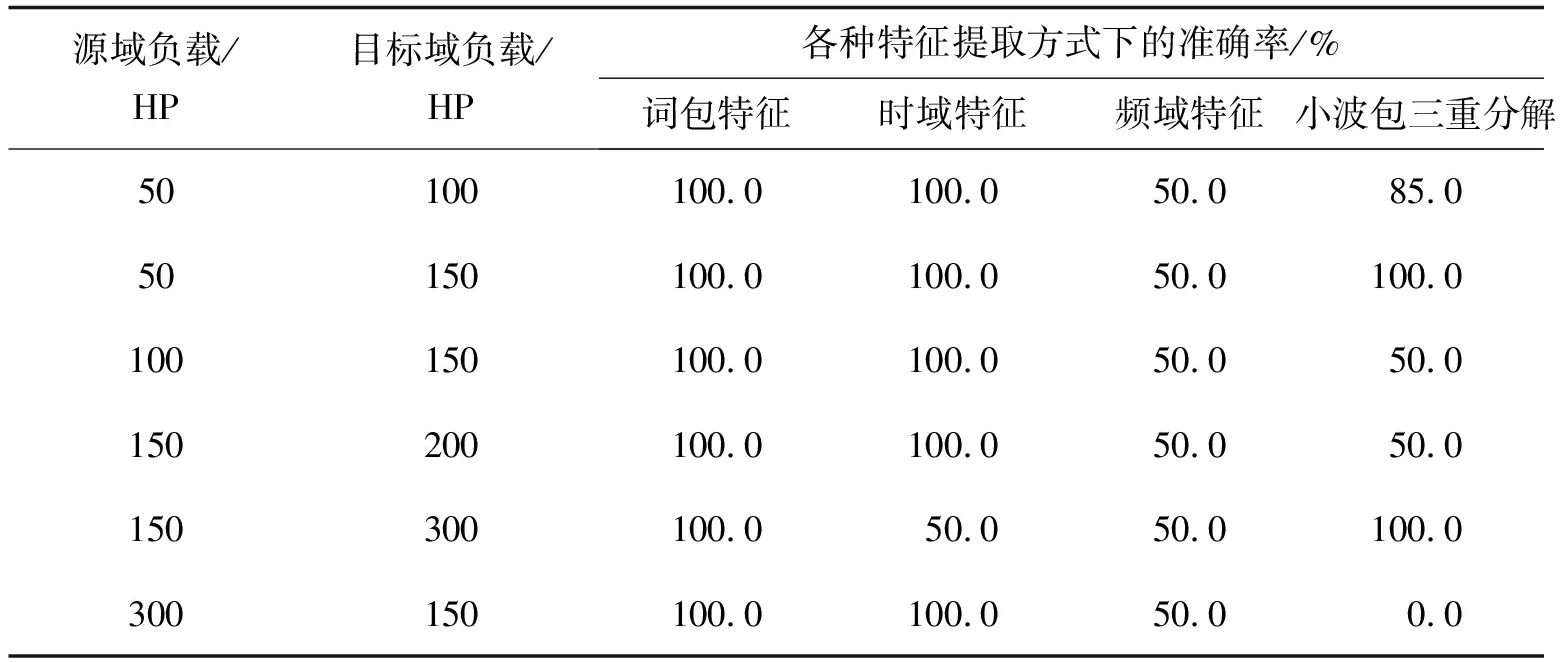
在这种情况下使用TCA拉近两者的距离,使它们趋于同一分布从而提取出准确的特征。对m段源域信号及n段目标域信号(每段信号长度相同)进行短时傅里叶变换,得到m+n个Nt*Nf的矩阵,把这些矩阵分为(m+n)*Nt个时间片段,每个时间片段上均为一个1 *Nf的数组,表示该时间片段能量在频域上的分布情况。再以这m*Nt个1*Nf的数组为源域,n*Nt个1*Nf的数组为目标域进行TCA,经过降维之后可以得到m*Nt个1 *Nf′的数组(Nf′ 图3 源域目标域 PSD分布对比Fig. 3 Comparison of PSD distribution between source domain and target domain 图4 迁移后源域目标域PSD分布对比Fig. 4 Comparison of PSD distribution between source domain and target domain after TCA 由图4可知源域数据PSD与目标域数据PSD经过迁移后分布近似相同,在这种情况下建立的词包模型能够更好地描述源域及目标域所指轴承的状态特征。 2.1.3 词包模型建立 得到源域及目标域迁移后的特征之后,便可以建立相应的词包模型。 对已知的所有分布情况做k-means聚类,每个分布表示为1 *Nf的数组,聚成k类,据此创建一个大小为k的词汇表,其中每个单词单独地对应某1个聚类结果,如图5所示。 F=[n(1),…,n(i),…,n(k)], (5) 式中n(i) 是单词wi在文档中出现的次数。 图5 聚类Fig. 5 Clustering 图6 词包Fig. 6 Bag of words 在不同情况下,k的取值也不尽相同,图7为凯斯西储大学数据集下某次迁移过程中某个轴承状态的诊断错误率随k值的变化。选取其中错误率最低的相应k值进行诊断。 图7 准确率随k值的变化Fig. 7 Accuracy changes with k 以源域数据做训练,以目标域数据做测试,构造相应的词包模型并训练若干分类器,包括SVM、KNN等,从中选择效果较好的分类器作为最终的分类器,不同的数据集下不同分类器的表现也不尽相同。 整个算法流程如图8所示。 图8 基于TCA和词包模型的轴承故障诊断流程Fig. 8 The process of bearing diagnosis based on TCA-BOW 在本次实验中,笔者将该算法应用于西门子SQI-MFS实验平台数据集、美国凯斯西储大学公开数据集以及机械故障预防技术协会MFPT(machinery failure prevention technology)数据集。 3.1.1 SQI-MFS数据集 图9 西门子SQI-MFS实验平台Fig. 9 Siemens SQI-MFS experiment platform SQI-MFS 实验平台由电机、变频器、轴承和支架组成(图9所示)。其中轴承型号为MBER-16K,实验台可以模拟各类轴承在不同转速和不同负载下的运行状态。实验中采集了36种运行状态下振动数据,分别为: 3种负载情况( 0,1,3 个转子负载) × 3种转速( 600,1 200,1 800 r /min) × 4种轴承(健康、滚珠、内圈、外圈) 。 3.1.2 凯斯西储大学数据集 美国西储大学实验平台由1个电机,1个转矩,1个传感器,1个功率计以及电子控制设备组成,其中被测试轴承种类为SKF轴承,实验中采集了16种状态下的信号,包括4种负载( 0,735,1 470,2 205 W),4种故障状态 ( 健康、滚珠、内圈、外圈)。其中,0 W负载下电机转速为1 797 r /min,735 W负载下电机转速为1 772 r /min,1 470 W负载下电机转速为1 750 r / min,2 205 W负载下电机转速为1 730 r /min。 3.1.3 机械故障预防技术协会MFPT数据集 该数据集由机械故障预防技术协会(MFPT)[14]提供。一个带有NICE 轴承的实验台收集了 270 磅负载下基线条件下的加速度数据(健康数据),采样频率为97 656 Hz,持续 6 s。共跟踪了10个外圈和7个内圈故障数据情况,其中外圈故障包括在 270 磅负载下,采样频率为 97 656 Hz,持续6 s的3个数据,以及在 11,23,45,68,91,113和136 kg磅负载下,采样频率为48 828 Hz,持续 3 s的 7 个数据;内圈故障包括在 0,23,45,68,91,113和136 kg磅负载下,采样频率为48 848 Hz,持续3 s的7个数据。 针对这3个数据集以某种工况下数据为源域,再以另一种工况下的数据为目标域进行TCA迁移,得到新的数据并建立词包模型以训练出相应的分类器后对目标域数据进行分类。具体步骤如下: 步骤1 选取某种工况下4种轴承状态(健康、滚珠故障、内圈故障、外圈故障)每种振动信号的10个片段,共计40个信号片段作为源域数据。 步骤2 选取另一种工况下的某种轴承状态的10个信号片段作为目标域数据。 步骤3 使用TCA和词包模型对轴承故障进行诊断,得出诊断结果。 步骤4 重复步骤2,3,得到以4种轴承状态数据为源域数据的40个诊断结果。 步骤5 计算并得到准确率。 3.2.1 与传统迁移成分分析对比 在传统的迁移成分分析中,通常从时域、频域、时频域中获取数据的特征。其在时域上提取峰值、平均幅值等13个时域特征。在时域上对频谱进行分析,提取频域统计特征并选取重心频率等5个频域特征。对数据进行小波包分解,得到8个时频域特征[15]。 1)西门子SQI数据集。 在西门子SQI数据集下将负载数量固定不变,进行跨频率的诊断,诊断结果如表1所示。 表1 SQI下基于各种特征提取方式的迁移成分分析准确率对比 从表1可以看出在西门子SQI数据集下使用词包模型进行特征提取再进行TCA,虽然在个别情况下准确率不算理想,但总体而言,相对于使用时域特征及时频域特征可以得到更高的准确率。在实际实验中,使用频域特征进行迁移成分分析得到的结果不太理想,所有的轴承均被诊断为外圈故障。 2)凯斯西储大学数据集。 在凯斯西储大学数据集下进行跨负载数量的轴承故障诊断。由于0负载滚珠故障数据缺失,故涉及0负载数据的忽略滚珠故障状态,仅对30个源域信号进行计算,诊断结果如表2所示。 表2 凯斯西储数据集下基于各种特征提取方式的迁移成分分析准确率对比 从表2可以看出在凯斯西储数据集下使用词包模型进行特征提取再进行TCA效果不错。整体而言比时域特征更高,与小波包分解差距不大。在实际实验中,使用频域特征进行迁移成分分析得到的结果也不太理想,所有的轴承均被诊断为内圈故障。 3)MFPT数据集。 MFPT数据集中仅有3个轴承状态(健康、内圈故障、外圈故障),因此只对这3种轴承状态进行研究。在实验过程中,由于健康数据均来自270磅负载情况下,所以只计算内圈及外圈共20个诊断结果的准确率,诊断结果如表3所示。 表3 MFPT数据集下基于各种特征提取方式的迁移成分分析准确率对比 从表3中可以看出,在MFPT数据集下,使用词包模型进行特征提取再进行TCA效果极佳。相对于时域特征及小波包分解具有更高的准确性与稳定性。在实际实验中,使用频域特征进行迁移成分分析得到的结果仍然不太理想,所有的轴承均被诊断为外圈故障。 3.2.2 与其他方法对比 在词包模型的基础上,分别运用TCA、PCA及核主成分分析(KPCA)算法对多组数据取平均值,结果如图10所示。 图10 词包模型TCA、词包模型PCA、词包模型KPCA的对比Fig. 10 Comparison of TCA-BOW, PCA-BOW and KPCA-BOW 由图10可知,使用TCA进行诊断时,随着数据组数的增加,准确率渐渐趋于稳定,始终保持在90%以上,相对地,使用PCA进行计算时准确率并不稳定且效果不佳,而KPCA虽然使用效果比PCA好但与TCA还是有一定的差距。 1)提出一种使用迁移成分分析和词包模型的变工况轴承故障诊断算法,对不同工况下的轴承振动信号进行迁移成分分析并建立相应的词包模型,并以此训练出分类器进行诊断。 2)在西门子SQI-MFS数据集、凯斯西储大学数据集、MFPT数据集下进行实验后,发现传统迁移成分分析使用的时域、频域及时频域特征整体而言效果欠佳,尤其是在频域下直接进行TCA效果较差(即使预先进行了归一标准化),相对而言,同时使用词包模型特征与TCA效果更佳。 3)实验证明了本算法在变工况轴承故障诊断方面的有效性,对于复杂工况下的生产,使用这种算法可以以较低的成本完成轴承故障诊断。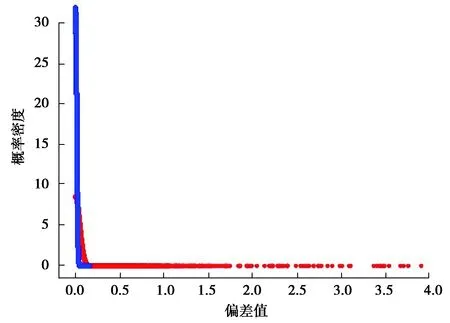



2.2 分类
3 实验结果
3.1 实验数据

3.2 实验内容

4 结束语
