从形变到质变 由学会到会学
——对2021年中考浙江金华卷第23题的赏析与启示
2022-06-24林胜威广东省化州市新安中学525133
林胜威 (广东省化州市新安中学 525133)
陈兴海 (广东省茂名市新世纪学校 525400)
2019年11月22日教育部发布的《关于加强初中学业水平考试命题工作的意见》(下简称《意见》)指出:初中学业水平考试命题要发挥引导教育教学作用,引导教师积极探索基于情境、问题导向、深度思维、高度参与的教育教学模式,引导学生自主、合作、探究学习.以素养为导向、提升试题科学化水平已成为各地中考试题命制的方向与共识.本文对浙江省2021年初中学业水平考试(金华卷)第23题进行评析,从中获得了一些有益的启示.
1 原题
背景:点A
在反比例函数的图象上,AB
⊥x
轴于点B
,AC
⊥y
轴于点C
,分别在射线AC
,BO
上取点D
,E
,使得四边形ABED
为正方形.如图1,点A
在第一象限内,当AC
=4时,小李测得CD
=3.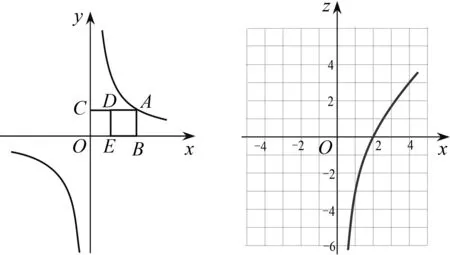
图1 图2
探究:通过改变点A
的位置,小李发现点D
,A
的横坐标之间存在函数关系.请帮助小李解决下列问题.(1)求k
的值.(2)设点A
,D
的横坐标分别为x
,z
,将z
关于x
的函数称为“Z
函数”.如图2,小李画出了x
>0时“Z
函数”的图象.①求这个“Z
函数”的表达式;②补画x
<0时“Z
函数”的图象,并写出这个函数的性质(两条即可);③过点(3,2)作一直线,与这个“Z
函数”图象仅有一个交点,求该交点的横坐标.2 评析
2.1 回归本源——考查对函数概念的理解
第(1)问求反比例函数中k
的值,求出点A
坐标代入即可(k
=4),是对“待定系数法”基本技能的考查.第(2)问引入了新函数——“Z
函数”,从题目给出的部分图象可知,这并不是熟知的三大函数(一次函数、反比例函数、二次函数)之一.学生欲求“Z
函数”的表达式,待定系数法“一设二代三求”的解题套路显然无能为力,必须回归到对函数本质的理解:函数是蕴含于变量之间的一种依存关系.求“Z
函数”的表达式应从z
与x
两者之间的关系入手,结合图1易得几何等量关系CD
+DA
=CA
,而由四边形ABED
为正方形得DA
=AB
,所以CD
+AB
=CA
,将几何等量关系“坐标化”即为故“Z
函数”的表达式为函数是中学数学的核心内容,也是历年中考的重点和热点.根据广东省教育考试院发布的2020年广东省初中学业水平考试数学试题评析的统计分析,三大函数是近五年广东省初中学业水平考试数学的高频考点.在各地的初中学业水平考试数学试题中,对函数考查的主要方向是函数的图象与性质、函数与几何的综合、函数的实际应用.这些考题是运用“已知”的图形性质、“已有”的函数模型去解决问题,是对旧知的记忆与运用,在一定程度上考查了学生的运算能力、推理能力、分类讨论思想和应用意识等.本题要求学生探索未知函数求表达式、性质与图象等,是基于函数概念的理解对新知进行探索,考查了学生对函数概念的理解.义务教育阶段函数的学习,要在学习“三大函数”基础上,形成利用函数的观点认识现实世界的意识,让学生会用函数的眼光观察世界、会用函数的思维思考世界、会用函数的语言表达世界.
2.2 累积经验——考查研究函数一般方法的掌握
第(2)题第②小问,要补画x
<0时“Z
函数”的图象,并至少写出这个函数的两条性质.学生没有现成的知识可凭借,需要利用“经验”对新函数进行研究.根据一次函数、反比例函数和二次函数的学习研究经验,研究函数的一般方法和步骤是:画函数图象、观察归纳特征、用数学语言描述性质.由“Z
函数”表达式,易画它的图象;而对函数图象的研究可从图象的形状、位置、增减性(单调性)、对称性等角度进行观察,最后用数学语言概括与描述如下:a.此函数的图象是由两个分支组成的曲线(形状).
b.此函数的图象关于直角坐标系的原点成中心对称(对称性).
c.当x
>0时,函数值z
随自变量x
的增大而增大;当x
<0时,函数值z
随自变量x
的增大而增大(增减性).基础知识、基本技能主要表现为结论性知识、事实性知识,基本思想、基本活动经验主要表现为在数学活动中形成和积累的过程性知识、策略性知识.从学生的数学素养培养来看,它并非单纯地通过接受数学事实性知识来实现,它更多地需要通过对数学思想的领悟、对数学活动经验的积累和条理化,以及对数学知识的自我组织等活动来实现.数学教学要克服“双基”教学中过于表层、追求熟练、缺乏对数学本质理解的弱点,让数学的思维方法、研究方法铭刻在头脑中,并内化成为让学生受益终生的必备品格和能力,就要引导学生对“所学知识”“所经历的活动”进行概括与归纳,上升为更一般的思想方法、原理观念.
2.3 学以致用——考查问题解决能力
通过关系分析得出函数表达式,再结合图象观察归纳函数性质,最后应用此函数去解决相关的问题,这是研究函数的“基本套路”.在①②小问的基础上,第③小问要求利用“新知识”解决“旧问题”:求直线与函数图象的交点.由几何直观知,当直线与“Z
函数”图象仅有一个交点时,存在“相交”与“相切”两种情况:a.第一种情况(相交):“Z
函数”图象不与y
轴相交,故平行于y
轴的直线与“Z
函数”图象仅有一个交点,且直线过点(3,2),可得交点的横坐标为3.b.第二种情况(相切):若从图形的角度看则难于求出切点,可转换为用代数的方法求解,考查学生对数形结合思想的领悟.可设直线的表达式为z
′=mx
+b
(m
≠0),将点(3,2)代入可求得b
=-3m
+2,故z
′=mx
-3m
+2.联立两函数表达式可得含m
的方程转化为整式方程得(m
-1)x
+(2-3m
)x
+4=0.当整式方程仅有一个解时,直线与函数图象仅有一个交点,求得交点的横坐标为4或2或6.初中学业水平考试主要衡量学生达到国家规定学习要求的程度,既要注重考查基础知识、基本技能,还要注重考查思维过程、创新意识以及分析问题与解决问题的能力.“旧知识”应用于“新问题情境”,注重的是问题解决中的知识迁移与运用;本题是“新知识”应用于“旧问题情境”,让学生不囿于原有知识藩篱或固有的思维模式,使得学生更关注于问题解决的数学策略、思路、方法等.德国2012年颁布的高中数学标准中,将“数学地解决问题能力”界定为学生“拥有恰当的数学策略去发现解决问题的思路或方法,并加以反思”.
3 启示
3.1 考查内容由“形变”向“质变”的递进
在《意见》颁布之前,《考试大纲》和历年中考试题是复习备考的两大必备资料,认真研究《考试大纲》和历年中考试题是复习备考的成功经验和基本要求.《考试大纲》指明了考试内容与范围,即明确了“考什么”;历年中考试题则蕴含了考查的形式与方法,即提供了“怎么考”的示范样例.相同的知识点,不同年份的试题只是在考查形式上变化(形变),而考查的内容实质没有变化(质变).例如,广东省2017—2019年中考试题的解答题部分对“方程与不等式”的考查,见表1.
表1
年份题号分值试题考查内容201921(8分)某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.(1)若购买这两类球的总金额为4 600元,求篮球、足球各买了多少个?(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?列方程组、不等式解应用题201820(8分)某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3 120元购买A型芯片的个数与用4 200元购买B型芯片的个数相等. (1)求该公司购买的A、B型芯片的单价各是多少元?(2)若两种芯片共购买了200个,且购买的总费用为6 280元,求购买了多少个A型芯片?列方程组解应用题201719(6分)学校团委组织志愿者到图书馆整理一批新进的图书.若男生每人整理30本,女生每人整理20本,共能整理680本;若男生每人整理50本,女生每人整理40本,共能整理1 240本.求男生、女生志愿者各有多少人?列方程组解应用题
通过对比发现,三年试题考查的是“根据具体问题中的数量关系列出方程(组)、不等式(组)”的建模能力和“解方程(组)、解不等式(组)”的运算技能.不同年度的考题只是问题情境和数据的
不同,对考生的能力要求没有实质性的改变.这在一定程度上导致在复习备考中出现“为考试而考试”的短视行为:只关注“能列会算”等基本技能的操练,忽略对方程、方程的解等概念的理解与思考.而在广东省2020年的中考试题中,除了基础知识、基本技能的考查外,还加强了对概念本质理解的考查:
(2020年广东中考第21题)已知关于x
,y
的方程组与的解相同.(1)求a
,b
的值;(2)若一个三角形的一条边的长为另外两条边的长是关于x
的方程x
+ax
+b
=0的解,试判断该三角形的形状,并说明理由.对“两个二元一次方组的解相同”的理解是解答本题的关键.“解相同”可以理解为两个方程组有“公共解”或“相同解”;两个方程组的“公共解”既满足方程组(I),也满足方程组(II);满足方程组(I)的解是方程①②的解,满足方程组(II)的解是方程③④的解.那么这个“公共解”是方程②③的共同解,方程组的解是方程①②③④的解.
面对此问题,学生没有固定的解题模式可模仿.因此,在复习备考中也就不能只是“死抠”题型,而要注重对数学概念本质的理解,以不变应万变!中考考查的内容与形式由“形变”到“质变”的递进,是“在新课标与高考评价体系的指引下,以高考为代表的大规模中学数学考试命题正在发生从能力立意到素养导向的重要转变”.
3.2 考查要求由“学会”向“会学”演进
学习是人类的生存本能,也是人类需要不断学习提高的能力,以适应不断发展变化的环境.2016年发布的《中国学生发展核心素养》总体框架指出,学会学习是自主发展素养的基本要点.课堂教学除了让学生“学会”具体知识、掌握特定技能,还要在知识技能的基础上培养关键能力,形成能够适应终身发展和社会发展需要的素养.用什么方式引导学生的数学思维活动,使学生在掌握知识的过程中学习数学思考方法,从学会思考逐步走向学会学习,是教材编写中需要认真思考和落实的主要任务.作为“指挥棒”的中考试题,除了考查学生是否“学会”了基础知识与基本技能,更要引导学生在学习中“学会学习”,即“会学”.例如,2020年贵州省遵义市中考数学第10题:
构建几何图形解决代数问题是数形结合思想的重要性,在计算 tan 15°时,如图3,在Rt△ABC
中,∠C
=90°,∠ABC
=30°,延长CB
使BD
=AB
,连结AD
,使得∠D
=15°,所以tan 15°类比这种方法,计算tan 22.5°的值为( ).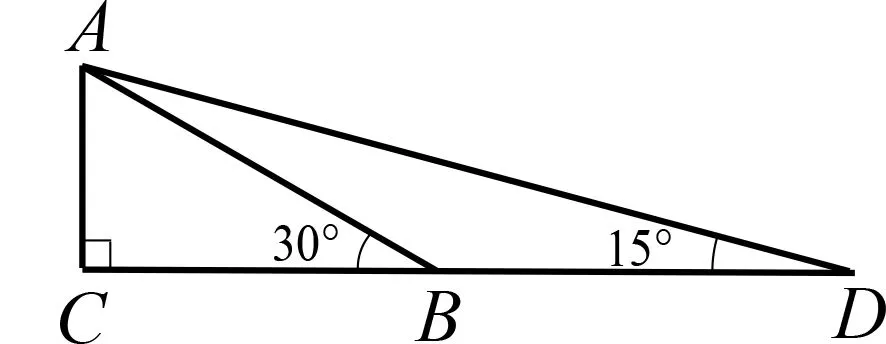
图3
学生要解决本题,除了掌握含根式的分式化简外,关键是通过题目给出的示例,学习领会其构造的方法,然后应用于所求的问题.此题考查的不是学生对具体知识技能的理解与掌握,而是对新知识的理解、迁移、运用的能力.学习能力在学习过程中培养,但不能仅停留于基础知识的记忆、基本技能的操练,还要对学习过程进行审视与反思,习得符合自已的科学的学习方法与策略,提升自我评估与调控的元认知水平,养成注重学习的学习习惯与品格意识,实现由“学会”向“会学”的演进.
