小学数学课堂提问的 时机和方式

金姝

问题是引发学生数学思考的动力与源泉，有效的课堂提问直接影响着学生的思考。因此，在教学中，教师要充分发挥课堂提问的效能，注意提问的时机和方式，适时地进行提问，引导学生积极思考，从而使学生进入学习的最佳境界，提高课堂教学效率。教学时教师既要把握提问的时机，又要注意提问的方式，做到以问促思，培养学生数学思维，提高课堂教学质量。

一、把握课堂提问的时机

苏霍姆林斯基曾说过：“教学的技巧并不在于预见课堂教学的所有细节，而在于根据当时的具体情况，巧妙地在学生不知不觉之中做出相应的变动。”在教学中，我们不仅要关注知识本身，更要关注知识背后的道理，回归数学本质，适时提问，启迪学生思维，促使学生积极思考。

（一）问在“质疑处”，激发学生思考

在数学教学中，教师经常会依据自己的经验，围绕教学内容来预设问题，为学生搭建解决问题的支架，从而达到预设的教学目标。教师要在学生有疑问时提出问题，从而促使学生深度思考。

例如，在教学人教版数学五年级下册“长方体的体积”时，上课伊始，教师问：“今天我们要学习的是长方体的体积，你们知道长方体的体积怎么计算的吗。”几乎全班学生都说知道，教师又问：“你们从哪里知道的？”学生的回答有：家长提前告知、自学课本、教师辅导等。既然学生都学会了，那么这节课学什么呢？若在教学中，学生仅限于知道“长方体的体积=长×宽×高”，那就不是真正的学习。教师要让学生主动“后退一步”自我反思自己“这节课学什么”，从而促使学生根据已知的内容来思考：“我们只知道计算公式，但不知道公式的意义。”关键的质疑，推动着学生对长方体的体积公式提出真实的问题，进一步对已知的公式进行批判性思考：“我们只知道长方体的体积计算公式，但不知道为什么要这样算。”“为什么長方体的体积=长×宽×高呢？”从而产生迫切的学习需求。伴随着问题的产生，学生的学习从公式化的“是什么”走向追求真理的“为什么”，逐步走向深度思考。

（二）问在“难点处”，启发学生思考

弗赖登塔尔认为：“数学是人的一种活动，如同游泳一样，要在游泳中学会游泳，我们也必须在做数学中学习数学。”因此，在“做数学”中，教师应该更清楚地意识到学生要亲历知识的形成过程，要把握知识重难点，适时追问，激起学生的思维碰撞，促使学生思维走向更深处。

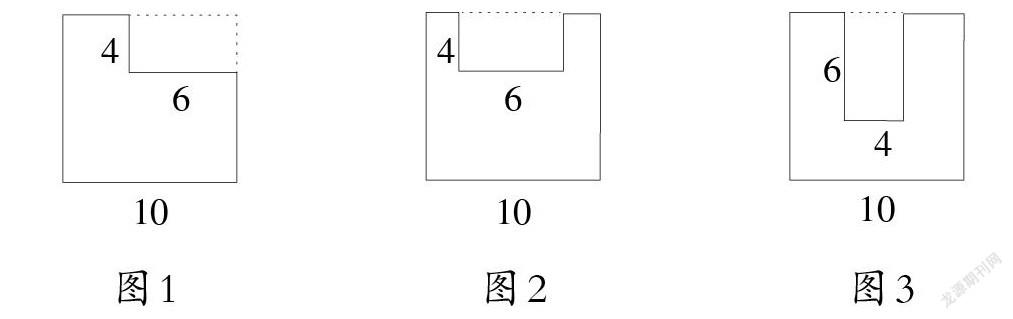
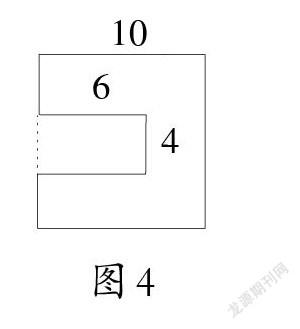
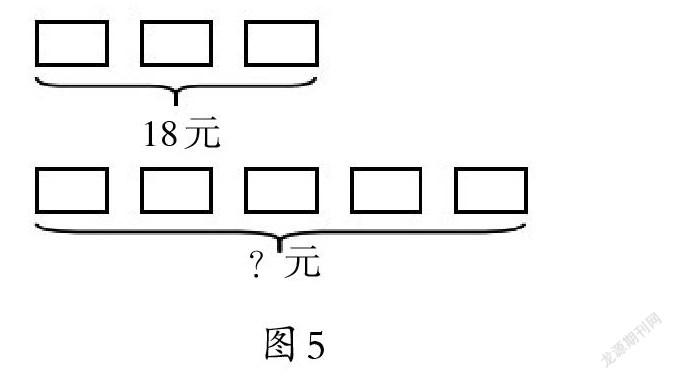
例如，在教学人教版数学三年级下册“周长和面积练习课”时，教师出示一道练习题：从边长是10厘米的正方形纸上，剪掉一个长6厘米、宽4厘米的长方形。小王想到了3种不同的剪法（如图1、图2、图3）。求剩下部分的周长和面积。

师：如何求出剩下部分的周长和面积？

（学生做题，教师巡视并于3分钟后提醒：小组内讨论，根据你们的计算结果有什么发现）

生：通过计算，我们知道它们的面积相等，都是76平方厘米;周长不相等，图1的周长是40厘米，图2的周长是48厘米，图3的周长是52厘米。

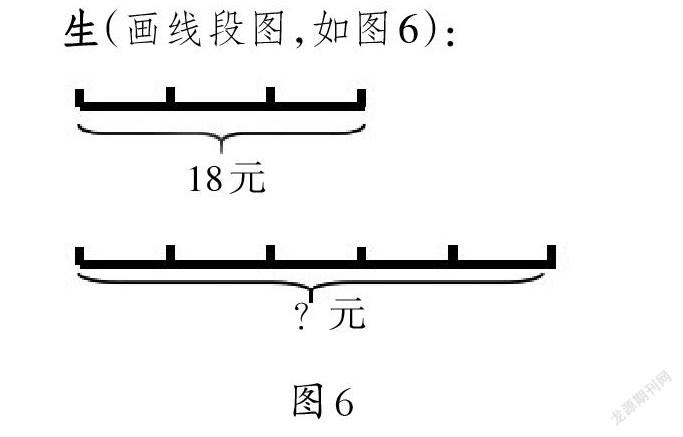
这时，有个学生提出问题，除了这3种剪法，还有其他剪法吗？顿时，全班学生脑洞大开，出现了第四种剪法（如图4）。

[6][4][10]

图4

师：你们真会思考，那现在能算出图4的周长和面积吗？

生（齐）：能。

师：谁来汇报？

生：周长是52厘米，面积也是76平方厘米。

师：咦，现在有什么新发现吗？

生：图4的面积和其他图形一样，但是周长和图3相等，与图1和图2不相等。

师：认真观察这4幅图，你们能完整地说说有什么新发现吗？

生：这4幅图的面积都相等，图3和图4的周长相等，因为它们都是从中间剪去一个长方形，而图1和图2中剪去的长方形，一个是沿着正方形的边剪，一个是从中间剪，所以它们的周长不同。

生：图形的面积相等，周长可能相等也可能不相等。

适时的提问，能引导学生在数形结合中进行数学思考，在开始计算时，学生通过独立计算再小组内讨论得出“剩余部分的周长不相等，但是面积相等”的结论。根据学生的认知和思考的“切入点”，在学生敢于提出疑问中出现了第四种剪法（如图4）后，就进行巧妙地追问：“现在有什么新发现吗？”学生发现了图4的面积和其他图形一样，但是周长和图3相等，教师顺势提问：“认真观察这4幅图，你们能完整地说说有什么新发现吗？”诱发了学生的思维活动，从而实现了“思考—探究—明理”的认识过程，使学生突破“图形的面积相等，但周长不一定相等”的难点。巧妙的追问，让知识深入浅出、思维走向深处，有助于开启学生思维对话。

（三）问在“错误处”，促进学生思考

《义务教育数学课程标准（2011年版）》指出：“教学中要合理地利用生成性教学资源，如交流过程中产生的新问题、新思路、新方法等，以提高教学的有效性。”课堂上，教师要善于捕捉和利用学生在动态学习中生成的错误资源，错误是思维的源泉，学生的练习错误，暴露出他们在思考过程中存在的漏洞，教师要巧用错误资源，引导学生在改错、纠错中不断进步、不断成长，探寻错误“根源”，促进思维发展，提升数学素养。

例如，在教学人教版数学二年级下册“小括号”一课时，教师出示一道题：工人每天上午工作4小时，下午工作5小时，平均每小时能做10个零件，请问工人每天可以做多少个零件？

师：根据提供的信息和问题，你们会列式吗？

师：你们有什么想说的吗？

（很多学生表示不理解）

生：运算顺序错了，应该先算乘法再算加法。

师：谁能看懂这个作品的作者为什么先算加法再算乘法呢？

（学生表示疑惑）

生：按他这样计算，先算乘法10乘4求的是4小时一共做了40个零件，再加上5个小时得到的零件应该是59。咦，那“59”表示的是59个小时还是59个零件呢？

师：是的，先算乘法再算加法的运算顺序与题意产生矛盾，该怎么办呢？

（顿时班级安静了）

生：要想先算4加5的话，我觉得要加“小括号”。

师：你太棒了。今天老师特别邀请了数学王国里的小括号帮助我们解决刚才的问题。

师：现在你们有什么想说的吗？

生：小括号真了不起，帮助我们解决了问题。

生：现在变成先算一天一共工作了9小时（上午的4小时和下午的5小时），再算10乘9的积。

教师及时捕捉和充分利用错误资源，可以拓展学生的认知。上述教学环节中，教师紧紧抓住一个非常有价值的课堂生成——学生的列式虽然错了，但可以结合题意正确计算。通过问题串，使学生有一种急于解决问题又不知道該如何解决的认知冲突，为“小括号”的出场做铺垫，顺理成章地让学生亲身经历“小括号”产生的重要性。在教师的引导下，学生从困惑中走出来，让思维在错误中“动”起来，课堂因错误而绽放精彩。

二、注意课堂提问的方式

问题是引发学生数学思考的动力与源泉，有效的提问直接影响着学生的思考。教学中，精心设计问题有助于引导学生深度思考，不但能激发学生的学习兴趣，而且能引导学生去探究、解决问题。因此，在数学教学中，教师要注意提问的方式，引导学生积极思考。

（一）启发式提问，引导学生思考

在教学中，教师要注重引发学生的思考，激发学生的学习潜能，鼓励学生大胆探索新知。为此，教师要设置问题，引导学生去思考、探究、解决问题。

例如，在教学“解决问题”时，有这样一道题：“3个小朋友去买同样的笔记本，小丽买3本用了18元，小华买5本，应付多少钱？如果小明用了42元，他买了几本？”学生读完题目后，久久望着题目无从下手。教师问：“大家为什么不动笔呢？”学生说：“题目讲了很多条件，很乱。”教师又问：“要求小华用了多少元，大家应选择哪些条件，能不能把这些条件摘录下来，使我们看得更清楚一些？”通过这个启发式问题，学生就立即动笔摘录，然后教师指名汇报。

生（摘录条件）：

小丽：买3本18元。

小华：买5本多少元？

生（画方框图，如图5）：

生（画线段图，如图6）：

生（列表）：

师：这样摘录就很清楚了，现在怎样求小华用了多少元呢？

生：要求5本多少元，必须先知道每本多少元。

生：因为他们买的是同样的笔记本，所以先从小丽入手，求出每本的价钱。

教学中，当学生遇到思维障碍时，教师要抓住时机，抛出有启发性的问题，帮助学生找到“突破口”，给学生留足思考的时间，引导学生独立思考、大胆探究。

（二）开放式提问，引导学生思考

《义务教育数学课程标准（2011年版）》明确指出：“学生的数学学习活动应当是一个生动活泼的、主动的和富有个性的过程。”这就要求教师实施开放性教学，为学生创造一个开放的教学环境，给学生提供一个开放的空间，让学生主动地投入学习之中。开放性问题给学生提供多角度、多侧面的思维空间，还能开阔学生的视野，让学生寻找更多的解决办法。

例如，教学“解决问题”时，有这样一道题：“小明家、小红家和学校在同一条路上。小红家到学校有312米，小明家到学校有155米，求小红家到小明家有多远？”教师问：“这道题目的已知条件和未知条件是什么？需要我们解决什么问题？仔细阅读题目，然后想一想，可能有几种情况？”一石激起千层浪，学生立即画出小红家、学校、小明家的示意图，探讨有几种情况，学生讨论得很激烈，教师再指名汇报。

师：哪个同学上来说说你的想法？

生：我认为小红家和小明家在学校的两边，就列式为312+155=467（米）。

生：我认为小红家、小明家和学校的位置关系可以有两种情况，我已经画出来了（如图7）。

第一种情况：小红家和小明家在学校的两侧，列式为312+155=467（米）。

第二种情况：小红家和小明家在学校的同一侧，列式为312-155=157（米）。

开放式问题为学生打开了思维的大门，给他们提供一个广阔的探究空间。学生独立思考、合作交流、分析讨论，创造性地解决了问题。

（三）猜想式提问，引导学生思考

牛顿说过：“没有大胆的猜想，就不可能有伟大的发明和发现。”猜想是学生依靠学过的知识，依据条件猜想结果，依据部分估计整体，根据已知想象未知的过程。在教学中，教师运用猜想可以营造探究学习氛围，激发学生积极思考，勇于探究，去获取新知识。

例如，在教学人教版六年级上册“分数的除法”时，教师先复习“分数乘法”知识，并向学生发问：“你们能利用学过的分数乘法来计算分数除法吗？”学生质疑：能否像分数乘法那样，用分子除以分子，分母除以分母？这时，教师没有表态，而是让学生去验证、去尝试，再指名汇报。

生：[825]÷[25]=[8÷225÷5]=[45]。

验算：[45]×[25]=[825]（算法正确）。

生：[1627]÷[23]=[16÷227÷3]=[89]。

验算：[89]×[23]=[1627]（算法正确）。

许多学生认为分数除法可以用分子、分母分别相除的办法来计算。这时有学生提出：[914]÷[78]怎样算？教师组织学生独立思考、互动交流，从而得出一般性的结论。

课堂提问促使学生进行猜想，猜想的过程也是解决问题的过程，从而提高了学生分析问题、解决问题的能力。

（作者单位：江西省余江韬奋学校）