中考数学中的基础题与能力题例谈

2022-06-23谭丽春周怡杉

读写算(下) 2022年4期

关键词：题型中考考查

谭丽春，周怡杉

中考数学中的基础题与能力题例谈

谭丽春，周怡杉

（南宁师范大学，广西南宁530100）

本文通过对中考数学中的基础题与能力题的思考，结合数学知识、数学技能、数学能力三者的关系，分析数学基础题和数学能力题的题型特点、解题方法及其教学策略，以期能够从教学实践方面对数学能力的培养有所启示。

四基；数学能力；基础题；能力题

义务教育阶段的数学课程总目标是：通过义务教育阶段的数学学习，学生能够掌握社会生活和进一步发展所需要的数学“四基”，增强发现问题和提出问题、分析问题和解决问题的能力。从中可以看出：《义务教育数学新课程标准修订（2011年版）》明确地将“发展‘四基’、培养和发展学生的数学能力”作为数学教育的目的之一。

要使新的课程改革得到真正的落实，教育评价的研究必须先行。为了体现“四基”与能力的考查，在中考数学中，数学基础题和数学能力题是基于“四基”与能力立意的命题方向的具体体现。中考是衡量学生是否达到毕业标准的重要依据，试卷结构必须科学，要综合考虑试卷的难度、信度、效度、可信度。所以中考数学试卷的命制既要通过基础题考查学生在数学学科知识与技能方面的水平，又要通过能力题考查学生的数学能力。下面本文将通过具体例子谈谈中考数学中数学基础题和数学能力题的常见题型。

一、中考数学中常见的基础题题型

数学基础题以考查学生数学基本知识和基本技能的理解和掌握为目的，寓数学思想方法和数学活动经验于问题情景之中。这类题目往往具有以下特点：①题目包含的信息容量小，一般包含1-2个数学命题和对象；②知识结构单一，要求能够对数学知识达到理解、识记的程度；③问题往往由一些基本的数学事实性知识（如定义、定理、公式、特定的证明等）和数学活动经验即可解决。

基础题首先考查的是数学课程标准中最基础、最核心的内容，即所有学生在学习数学和应用数学解决问题的过程中最重要、必须掌握的核心观念、核心思想、基本概念和常用技能。数学基础题注重考查“四基”，结合“四基”的特点可以将中考数学中常见的基础题题型分为以下几种：

（一）知识再认型

“知识再认”指的是对数学知识的再认与回忆。知识再认型题目考查的是学生通过问题情景的关联性，能否提取在学习过程中理解、记忆并系统化了的数学知识，即考查的是学生对基本知识的理解、掌握以及重组，同时也是检验学生数学知识掌握程度的重要途径。

例1 (2019年广西南宁中考)2019年6月6日，南宁市地铁3号线举行通车仪式，预计地铁3号线开通后日均客流量为700000人次，其中数据700000用记数法表示为（）

A.70×104B.7×105C.7×106D.0.7×106

（二）基本演算型

数与代数是初中数学课程的重要组成部分，数与代数部分包括数与式、方程与不等式、函数。而数的运算始终贯穿数与代数学习的全过程，所以学生的运算水平在数学学习中至关重要，也是中考考查内容之一。

例2 (2019年广西南宁中考)下列运算正确的是（）。

基本演算型的题目要求学生能够根据法则和运算律正确地进行运算，更高层次的要求是学生能够根据算式特点巧妙地选择合适的公式简化计算。基本演算型的题目是考查学生运算水平的重要途径。

（三）基本操作型

“空间观念”是《义务教育数学新课程标准修订（2011年版）》提出的十个核心概念之一，文中并没有对“空间观念”的内涵作具体的描述，但从四个方面对它的特征进行了描述，其中包括能够描述图形的运动和变化、依据语言的描述画出图形。所以能够依据图形的结构、关系，对图形进行分析、操作也是中考数学的考查内容之一。

例3 如图，在△中，=，∠=40°，观察图中尺规作图的痕迹，可知∠的度数为（）。

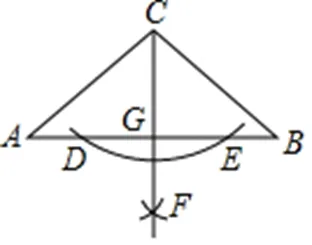
（四）基本方法应用型

数学思想和数学方法以数学基本知识和基本技能为载体，是数学学习和教学的精髓。以知识为载体的数学思想与方法是意识形态的，看不见、摸不着，所以对于数学思想和数学方法的考查，要以试题为媒介。

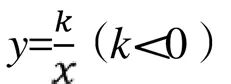
以上是中考数学中常见的基础题类型，对于基础题，直接运用基本知识技能、思想方法以及基本经验即可解决。基础题在中考数学试卷中比重较大，基础题重在考查“四基”，在数学学习中，学生要加深对知识的理解，要梳理知识的脉络，牢固掌握数学知识，不能死记硬背，理清新知识与旧知识的区别与联系，将新知识重组建构，形成完整的知识体系。教师在数学教学过程中要反复渗透数学思想，引导学生总结、归纳数学方法。总之，一个好的数学教学，是能够把数学知识、数学方法、数学思想、数学思维融为一体的教学。

二、中考数学中常见的能力题题型

综合近几年的试题来看，中考数学中的能力题往往具有以下特点：①题目包含的信息容量大，一般包含多个数学命题和数学对象，从而能够实现不同数学知识和数学思想方法的融合；②知识的综合性和层次性增强，要求对数学知识的理解水平能够达到系统化和具体化，重建或调整认知结构达到知识的融会贯通，并使知识得到广泛迁移的程度；③问题的探索性和创造性增强，问题解决的思路往往会有多个方向，需要依据数学知识的理解和数学思维对解题方案进行及时控制和调整，在一定程度上能够检测学生的数学能力。

数学能力是在获得数学知识和数学技能的基础上，通过广泛迁移，不断概括化、系统化，即类化而实现的。数学能力是数学技能的进一步沉淀与升华。数学基础题的训练能够为学生搭建牢固的基础，数学能力题可以使学生在学习上有进一步的突破。数学能力题综合性强，解法灵活多变，从近几年的中考数学来看，中考数学中常见的能力题题型有以下几种：

（一）动态型问题

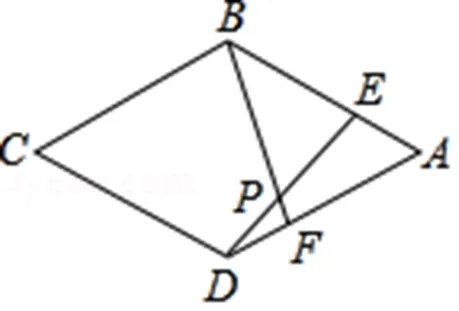
动态几何问题常见的解决方法是以静代动，常常通过对问题中的某些点（常取特殊位置）的动态变化查找动点的轨迹，大胆预测动态图的形状，然后再进行逻辑推理的证明。以图形的动态变化考查学生对点、线、面之间的位置关系等基础知识的掌握及一定的作图能力和几何直观能力，要求学生熟练掌握图形的相对位置关系。

（二）存在性问题

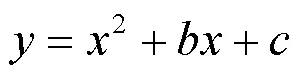
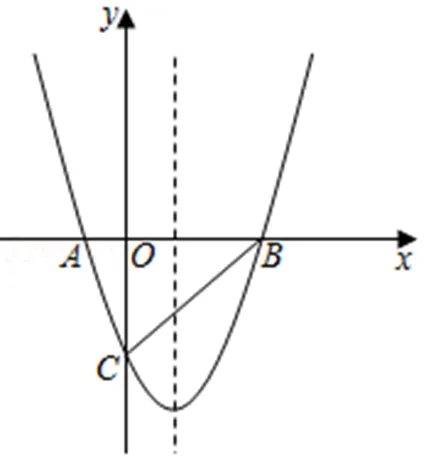
（1）求该抛物线的函数解析式。

几何法要求学生能够画出所有符合条件的平行四边形，对学生的图形感知能力要求很高。而且本题以二次函数为背景，而平面直角坐标系作为数与形的桥梁，在此前提下，显然本题的解题思路采用代数法更简便。

（三）新定义题

新定义题要求学生能够在现有知识的基础上，经历类比、迁移、概括、抽象的过程理解一个新定义，并能够用现有知识和语言重新表述新定义的内涵。

这个题目是常见的新定义题型，最关键的是要理解a×b的运算法则。本题目经历了从旧知到新知、从新知到实际应用的两次迁移，充分考查了学生的类比迁移能力，学生需经历尝试、探索、归纳、概括、抽象的完整思维过程，充分体现了学生的数学探究能力。此类题要求学生具备扎实的基础知识、理解阅读能力，从而能够根据旧知识理解新定义，并运用新定义解决数学问题。

（四）阅读理解题

∴AE=DF。

【类比探究】问题①，如图2，在正方形ABCD的右侧作等腰△，=，AD=4，连接AE，求△的面积。

解：过点E作EF⊥CD于点F，连接AF。

请将余下的求解步骤补充完整。

【拓展应用】问题②，如图3，在正方形ABCD的右侧作正方形CEFG，点B、C、E在同一直线上，AD=4，连接BD、BF、DF，直接写出△的面积。

阅读理解题是给定一段阅读材料，要求学生通过对阅读材料的理解、加工、整理，提取出其中蕴含的数学知识要点，领会其中的数学方法，并能够类比迁移，应用到新的问题情景中。这类题目主要考查学生的阅读理解能力和信息提取能力。

三、结论

中考作为学生学业成绩测量的一种手段，既是对数学知识、数学技能方面的考查，也是对学生在学习过程中表现出来的各种数学能力的程度、水平的测量。在数学学科中，数学知识与技能是显性的教学目标，数学能力目标则是以内隐的形式蕴含其中的教学目标。所以在数学教学过程中，教师要钻研教材，挖掘蕴含的数学能力，通过学科总目标和课时目标中的知识技能、数学思考、问题解决、情感态度等渗透对学生数学能力的培养。