基于达布变换的带三角势的Gross Pitaevskii方程的孤子解

刘淑丽，张金玉，李春晖，王晓丽

(齐鲁工业大学(山东省科学院) 数学与统计学院，山东 济南 250353)

非线性薛定谔方程形式为

iφt+φxx+2|φ|2φ=0,

(1)

这是一个重要的可积方程[1]，与光纤通信等物理中的非线性问题有密切的联系[2]。Gross Pitaevskii(GP)方程是一类带势函数项的非线性薛定谔方程，经常被用来模拟玻色-爱因斯坦凝聚中波函数的演化[3], GP方程的孤子解对玻色-爱因斯坦凝聚特性及其他物理问题的研究有十分重要的意义[4-6]。求孤子解有各种各样的有效方法，如逆散射法[7]、贝克隆变换[8]、Hirota双线性法[9]、达布变换[10]等。其中达布变换是通过给定非线性演化方程的一个“种子”解，进而寻找该方程另外一个显示解的有效方法，被广泛地应用于AKNS系统(1+1)维孤子方程[11]、2n维Lax可积系统[12]等。达布变换是法国数学家达布在1882年研究一维薛定谔方程的特征值问题时发现的，其基本思想是通过与可积方程的Lax对相联系的线性偏微分方程的解来构造可积方程的解。本文基于达布变换，考虑了一个带三角势的属于AKNS系统(1+1)维的孤子方程，即玻色-爱因斯坦凝聚态中一类带三角势的GP方程

iφt+φxx+2|φ|2φ+2[sin(ωt)+cos(αt)]φ=0,

(2)

其中φ(x,t)是关于空间变量x和时间变量t的复包络波函数，下标表示偏导数，参数ω、α是任意非零实常数。第二项和第三项分别表示色散和非线性效应，第四项描述了玻色-爱因斯坦凝聚中的外谐波阱势。

1 达布变换

容易求得方程(2)的Lax对为

Φx=UΦ,Φt=VΦ，

(3)

其中

(4)

(5)

定理1设方程(2)的n次达布变换为

Φ(n)=Dn(λ)Φ,

(6)

其中达布矩阵Dn(λ)=λnE+λn-1Sn-1+…+λS1+S0，E为二阶单位矩阵，Si=Si(x,t)(i=1,2,…,n-1)为一个关于x,t的二阶方阵。这里Φ为Lax对(3)的特征函数，Φ(n)为Lax对

(7)

的特征函数。其中，U(n)、V(n)与U、V具有相同的形式，并用一个新的势能函数φ(n)代替φ，即

(8)

(9)

则方程(2)的n孤子解表达式为

φ(n)=φ+2i(Sn-1)12,

(10)

其中(Sn-1)12表示矩阵Sn-1的第一行第二列元素，φ为方程(2)的一个“种子”解。

证明：将式(8)中U(n)及达布变换(6)代入新Lax对(7),比较λn的系数可以得到

P(n)=P+i[J,Sn-1],

(11)

由式(8)中P(n)和式(4)中P的表达式，我们可以推导出方程(2)的n孤子解表达式

φ(n)=φ+2i(Sn-1)12。

(12)

定理2设特征函数Φ(j)=(fj,gj)T满足代数方程

Dn(λ)|λ=λjΦ(j)=Dn(λ;λ1,λ2,…,λ2n)|λ=λj(fj,gj)T=0,(j=1,2,…,2n)，

(13)

则定理1中的函数矩阵Sn-1可以表示为[13]，

(14)

其中

2 孤子解

D1(λ;λ1,λ2)|λ=λjΦ(j)=D1(λ;λ1,λ2)|λ=λj(fj,gj)T=0,(j=1,2)。

(15)

这里一次达布变换

(16)

由定理2知，

由定理1知，方程(2)的单孤子解为

(17)

D2(λ;λ1,λ2,λ3,λ4)|λ=λjΦ(j)=D2(λ;λ1,λ2,λ3,λ4)|λ=λj(fj,gj)T=0,(j=1,2,3,4)。

(18)

这里二次达布变换

(19)

由定理2知，

同样，由定理1，我们可以得到方程(2)的双孤子解为

(20)

其中

3 解的性质

取“种子”解φ=0，则Lax对(3)为

(21)

通过线性谱问题(21)的解，易得关于谱参数λj(j=1,2,…,2n)的特征函数

Φ(j)=(fj,gj)T,fj=e-iρj,gj=eiρj,

(22)

其中

3.1 单孤子解的性质

φ(1)=2b1eiγ1sech(2b1x+8a1b1t),

(23)

(24)

且有

|φ(1)|2=4b12sech2(2b1x+8a1b1t),

(25)

取参数a1=b1=1，画出方程(2)的单孤子解图像，如图1所示。我们可以看到，图1模拟了一个亮的单孤立波，且孤立波的振幅没有变化。

图1 单孤子解x-t-|φ|2图像Fig.1 Images of a single soliton solution x-t-|φ|2

3.2 双孤子解的性质

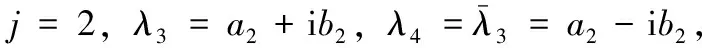
(26)

其中

且有

(27)

取值后画出方程(2)的双孤子解图像。如图2所示，两个孤波碰撞时产生能量，在碰撞后，波的形状和振幅保持不变。

为了进一步探讨特征函数中光谱参数和自由参数对孤波的影响，另取两组值，可以得到下列双孤子解图像，如图3、图4所示。对比图2～4可得，两波的传播方向与参数a1、a2的取值相关，二者的差值越大，两波的夹角越大；波的高度与b1、b2的取值相关，b1、b2值越大，波越高。

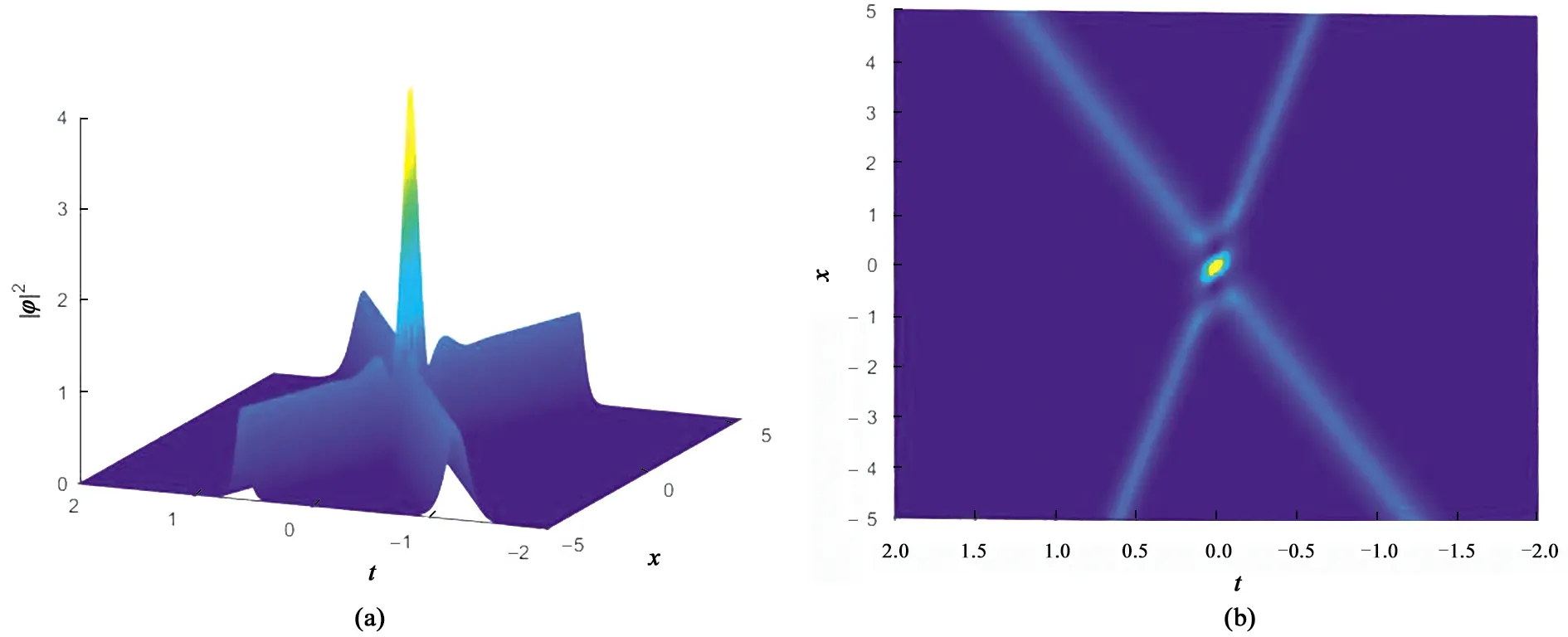
注：a1=-1,a2=2,b1=b2=α=ω=1。图2 双孤子解x-t-|φ|2及密度图Fig.2 Images of double soliton solutions x-t-|φ|2 and a density map

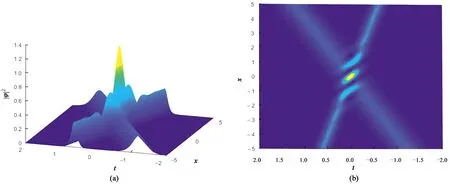
注：a1=-1,a2=2,b1=0.5,b2=0.6,α=ω=1。图3 双孤子解x-t-|φ|2及密度图Fig.3 Images of double soliton solutions x-t-|φ|2 and a density map

注：a1=1.2,a2=1.5,b1=b2=α=ω=1。图4 双孤子解x-t-|φ|2及密度图Fig.4 Images of double soliton solutions x-t-|φ|2 and a density map

4 结论

本文研究了一类带三角势的GP方程，基于达布变换给出了该方程n孤子解的表达式，并着重对单孤子解和双孤子解进行了数值模拟。通过图像可以明显看出，单孤子解为亮孤子解，在传播过程中保持形状不变；双孤子解中两个波碰撞时产生能量，两波碰撞后保持原来的幅度、形状和速度不变，且两波的传播方向与参数a1、a2的取值相关，二者的差值越大，两波的夹角越大；波的高度与b1、b2的取值相关，b1、b2值越大，波越高。本文中研究的GP方程可被广泛应用于等离子体物理、非线性光学等领域，尤其是可以用来模拟玻色-爱因斯坦凝聚波函数的演化。本文通过选取不同的参数探讨了对孤子传播的影响，有助于我们更好地理解非线性波的行为，对玻色-爱因斯坦凝聚特性及其他物理问题的研究具有十分重要的意义。