分级加载作用下砂砾料滞回曲线形态特征试验研究
2022-06-23王景
王 景
(新疆水利水电勘测设计研究院,新疆乌鲁木齐 830000)
1 引言
新疆地区砂砾石分布广,开采成本低,综合单价仅为堆石料的50%[1], 因此被广泛的应用于土石坝工程中。砂砾料的阻尼比是坝体动力计算的重要参数,是评价坝体抗震性能的重要依据。 动荷载作用下土体的动应力-动应变关系曲线为滞回曲线,其形态特征反映了土体的变形、刚度和能量消散等动力特性[2-3]。滞回曲线与骨干曲线共同构建了土体在循环动应力作用下本构模型,是动力参数分析计算和动力响应的重要依据。 目前,国内外学者对土体的滞回曲线展开大量的研究。罗飞等[4-6]对黄土和黏土滞回曲线展开研究,定量描述两种滞回曲线的特征;黄娟等[7-8]通过研究泥炭质土的动力特性,定量分析其滞回曲线特征。 根据以往学者的研究发现,对于滞回曲线形态特征的研究大多以粒径较小的土体作为研究对象,而对于大粒径的砂砾料其滞回曲线的特征的研究相对较少,因此,本文结合新疆特有砂砾石坝料开展室内大型动三轴试验,根据滞回曲线的基本特征分析不同围压作用下砂砾料滞回曲线形态的变化,对砂砾料滞回曲线进行定量描述,探求砂砾料在分级加载模式下滞回曲线形态变化特性。
2 三轴试验
2.1 试验设备
本次试验采用新疆农业大学岩土工程实验室的WYS-2000 大型多功能动静三轴试验机,如图1所示。主要参数为:试样尺寸φ300×700mm,最大轴向静荷载为2000kN;最大静围压5.0MPa;最大轴向动荷载为1000kN,最大动围压3MPa,轴向振动频率0.1~10Hz,幅值±70mm~±1mm,试验主机刚性大,自动化程度高,操作简单,测量数据精度高。

图1 WYS-2000 大型多功能动静三轴试验机
2.2 试验土样
本次试验砂砾料为新疆NY 水库工程坝料,最大粒径为600mm, 为满足室内试验仪器尺寸的要求,依据《土工试验方法标准》(GB/T50123-2019)[9]通过等量替代法对现场原型级配进行缩尺, 缩尺后砂砾料最大粒径为60mm,室内试验级配曲线如图2 所示。 通过试验测得试验级配下砂砾料的最大干密度ρdmax 和最小干密度ρdmin,按相对密度0.85 控制砂砾料的制样干密度,如表1 所示。
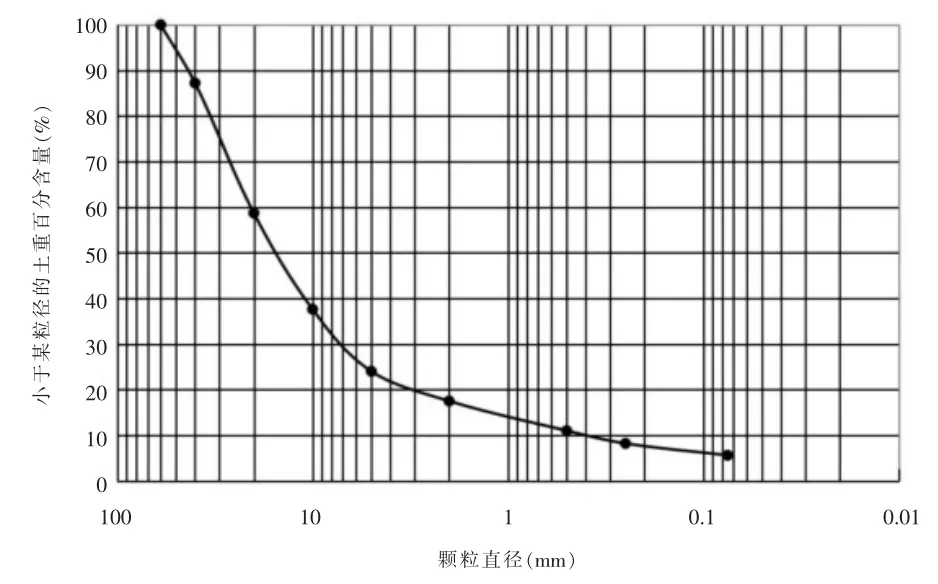
图2 砂砾料室内试验级配曲线

表1 砂砾料试验密度 (g/cm3)
2.3 试验方法
根据试验级配称取每一级砂砾料, 加适量的水拌和均匀,平均分成七份,分七次倒入固定好橡皮膜的承膜筒内并击实,为达到设计制样干密度,每层试料击实后的厚度为100mm。 试样成型后对其抽真空50min 后再进行固结, 当体变趋于稳定时认为试样固结完成,开始进行动力试验。 本次试验初始固结比Kc 为1.5 和2.0, 振动频率为0.333Hz, 波形采用正弦波, 每级动应力下振动6次。 具体加载示意图如图3 所示,试验方案如表2所示。
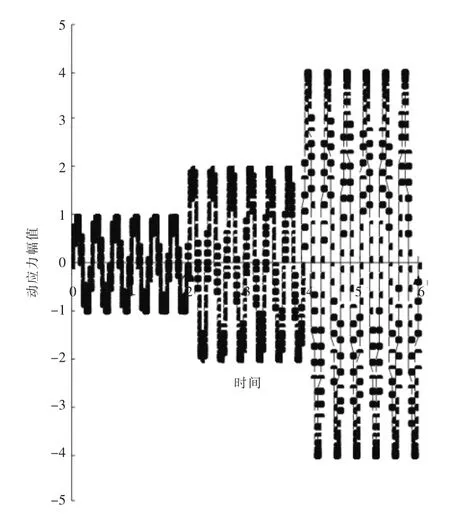
图3 加载示意图
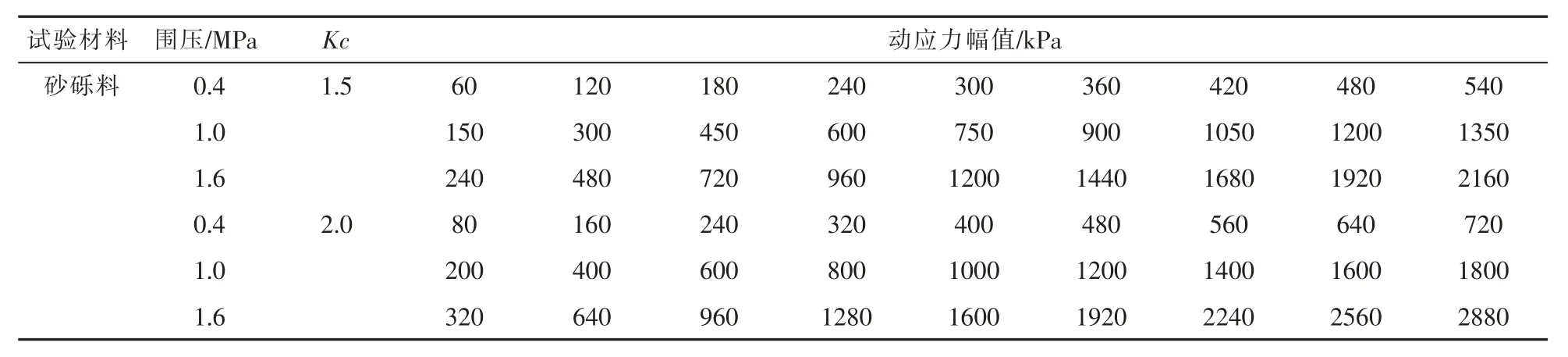
表2 不同固结比作用下轴向动应力幅值
3 砂砾料滞回曲线形态特征
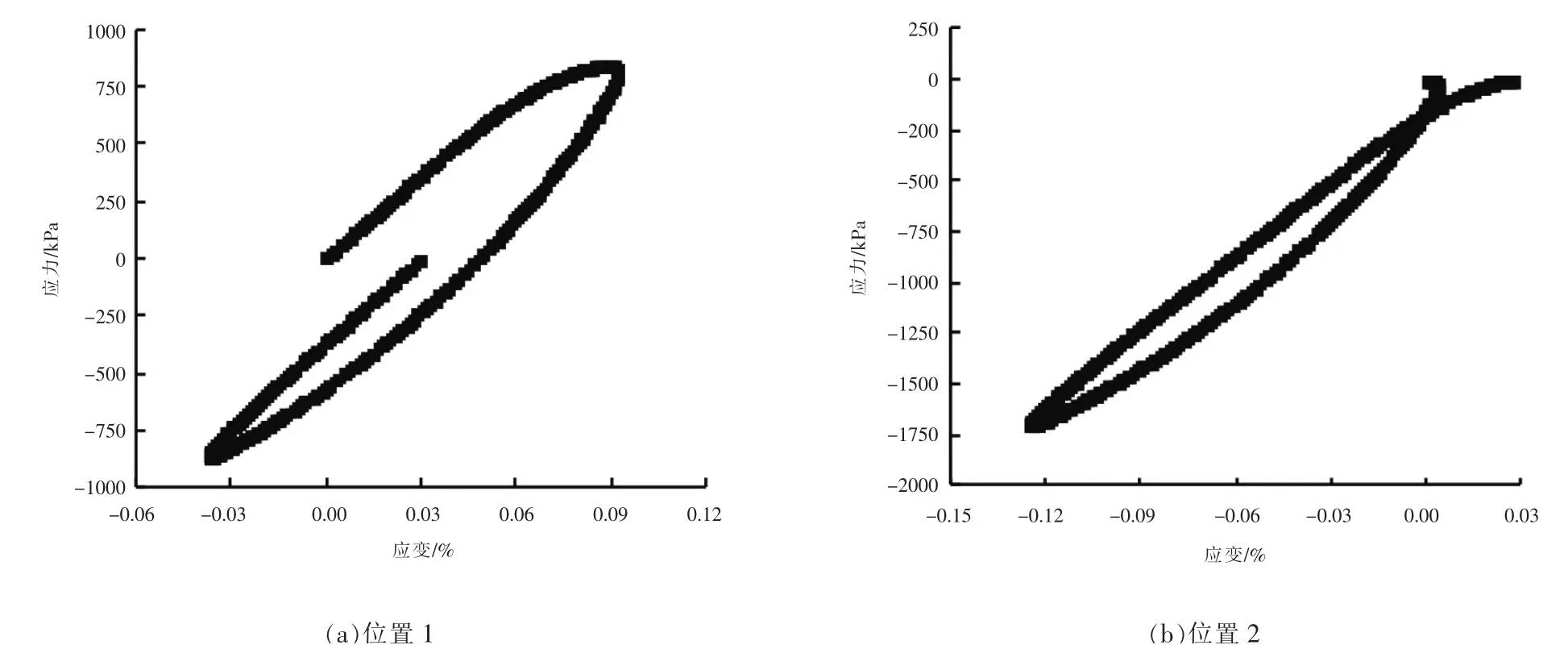
由于不同材料的应力应变关系存在差异,滞回曲线的形态特征也有所不同。 砂砾料属于黏弹性材料, 不同初始加载位置所对应的滞回曲线形态也不相同。 由于仪器精度高,自动化程度高,本次试验采集数据较多且连续, 可直接通过采集的数据绘制滞回曲线。不同初始加载位置(图4 中1、2、3、4 位置)所对应的滞回曲线如图5 所示。 由图可知, 不同初始加载位置所对应的滞回曲线不闭合且形态不相同。 当从位置2 加载时,滞回曲线出现一个交叉点, 此时运用等效阻尼比计算方法得到的滞回曲线的面积误差较大, 不利于后期阻尼比的计算。
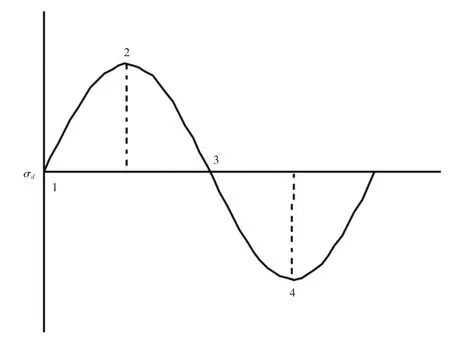
图4 全周期加载曲线
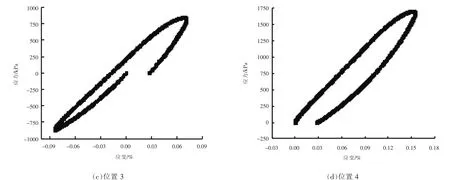
图5 不同加载位置处的滞回曲线
4 结果与分析
为便于计算和比较分级加载作用下砂砾料滞回曲线的形态特征, 本次试验选择4 位置进行计算分析不同加载比作用下分级加载时滞回曲线特征参数的变化规律。
4.1 残余应变量εp
砂砾料在循环荷载作用下产生残余变形,滞回曲线终点与起点之间的差值即为动力循环荷载一个周期内产生的残余应变量εp。 εp的大小反映了滞回曲线的不闭合程度, 同时反映了材料残余塑性应变大小,εp越大,不闭合程度越大,残余塑性应变越大。 图6 为不同动应力作用下滞回曲线,由图可以看出不同动应力作用下砂砾料残余塑性应变差异较大,εp随着动应力的增大而增大。 由于本次试验在不同围压下仅选用一个试样进行分级加载, 分析残余应变量试验结果时采取累加的方法,结果如图7 所示。 由图7 可知,相同动应力水平条件下,固结比相同时,残余应变量随着围压的增大而减小,围压相同时,随着固结比的增大残余应变量不断减小, 围压和固结比的提高使得骨料挤压密实,材料的塑性应变削弱。
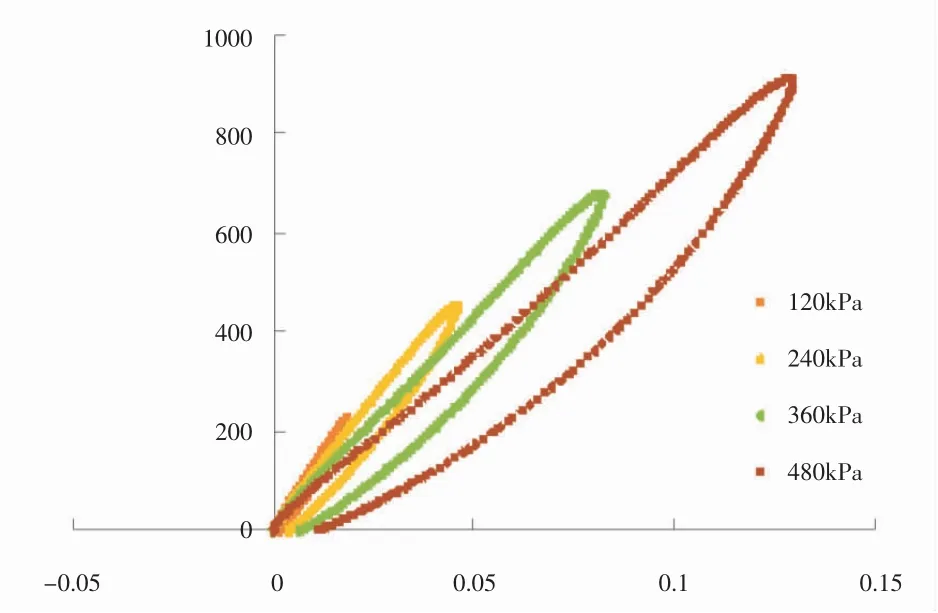
图6 不同动应力作用下滞回曲线
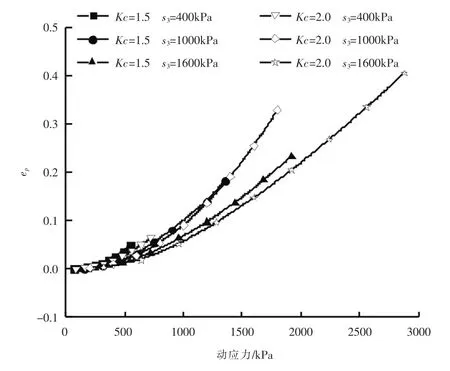
图7 不同围压和固结比作用下残余应变量与动应力关系
4.2 滞回曲线长轴斜率k

滞回曲线向应变轴的整体倾斜程度反映了材料的弹性性能及刚度。 由文献6 可知,滞回曲线的长轴与应变轴的夹角为θ,令k的大小反映了滞回曲线向应变轴的倾斜程度,k越大,滞回曲线向应变轴的倾斜程度越小,即材料的弹性性能越好,刚度越大;反之,滞回曲线向应变轴的倾斜程度越大,材料的弹性性能越弱,刚度越小。 通过本次试验绘制滞回曲线长轴斜率与动应力的关系曲线如图8 所示。 由图可知,随着动应力的增大,砂砾料长轴斜率不断减小,滞回曲线向应变轴倾斜程度不断增大, 材料的弹性性能不断减弱。 动应力相同时,长轴斜率随围压的增大而增大,随固结比的增大而增大,即围压和固结比的增大提高砂砾料的密实度, 增强砂砾料颗粒间的摩擦和咬合度,有效提高砂砾料的弹性性能,提高材料刚度。
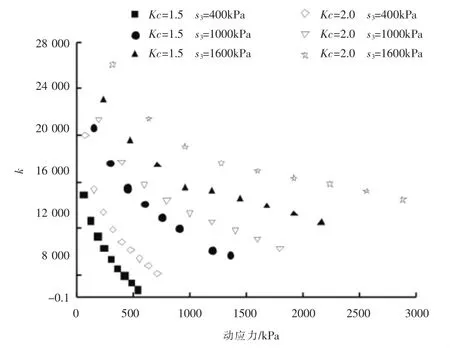
图8 不同试验条件下长轴斜率与动应力关系
4.3 滞回曲线面积
滞回曲线的面积表征了材料吸收动应变能的能力及抗震性能。 由于残余应变的影响,滞回曲线不闭合,为计算滞回曲线的面积,根据已有研究[10]对本次试验结果进行整理, 不同试验条件下滞回曲线面积如图9 所示。 由图可知,随着动应力的增大,各试验条件下滞回曲线面积不断增大。 围压和固结比对砂砾料滞回曲线的面积影响较大, 相同动应力作用下, 滞回曲线面积随围压的增大而减小,随固结比的增大而减小,即围压和固结比的增大提高砂砾料的密实度, 增强砂砾料颗粒间的摩擦和咬合,砂砾料的刚度提高,材料吸收的动应变能减少。
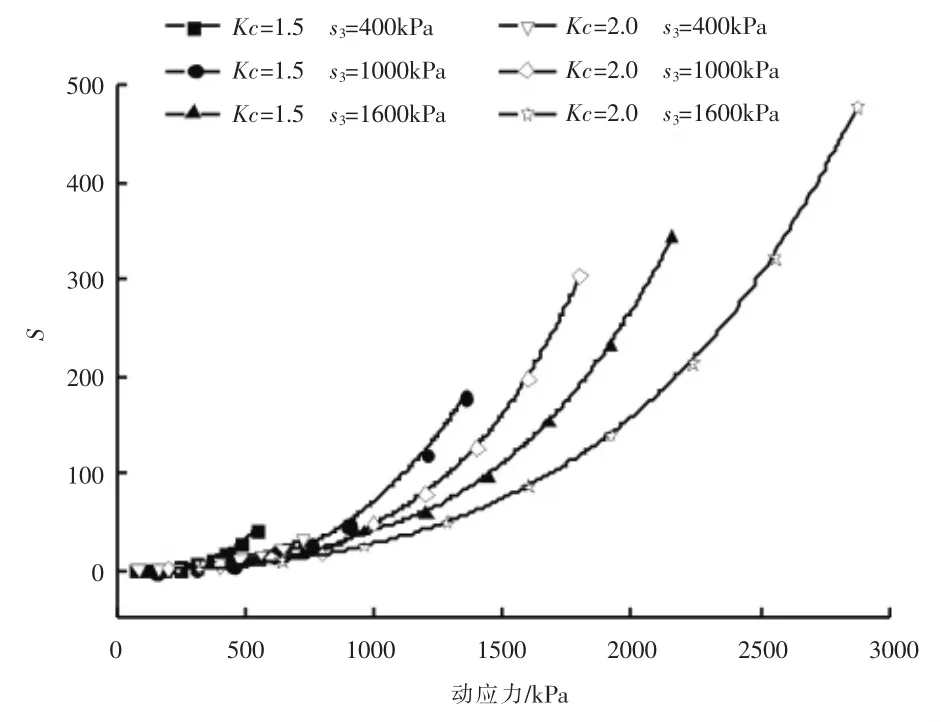
图9 不同试验条件下滞回曲线面积
5 结论
通过室内动三轴试验研究不同固结比作用下分级加载时砂砾料滞回曲线形态特征变化, 主要得出以下结论:
(1)砂砾料属于黏弹性材料,不同初始加载位置所对应的砂砾料滞回曲线形态与土体的滞回曲线形态相似。
(2)相同动应力水平条件下,围压和固结比的增大,降低砂砾料的塑性应变,提高砂砾料的弹性性能,提高材料刚度。
(3) 围压和固结比对砂砾料滞回曲线的面积影响较大,相同动应力作用下,滞回曲线面积随围压的增大而减小,随固结比的增大而减小,即围压和固结比的增大提高砂砾料刚度提高, 材料吸收的动应变能减少。 □
