基于时移生产动态测井资料的剩余油饱和度计算方法及其应用

2022-06-23平海涛秦瑞宝李雄炎刘小梅

中国海上油气 2022年2期

平海涛秦瑞宝李雄炎魏丹刘小梅

(中海油研究总院有限责任公司北京 100028)

在水淹层评价过程中，产水率是水淹级别定量划分的重要指标，建立储层静态参数(含水饱和度)与动态参数(产水率)之间的定量转换关系至关重要。含水饱和度评价通常以基于岩石物理方法的模型研究为主，另外国外一些学者也从非阿尔奇方法和油藏的角度开展了饱和度计算模型的研究[1-5]。而生产动态测井或生产测试资料可以获得油藏条件下的产水率，但与剩余油饱和度之间的关系研究较少。因此，开展油藏条件下产水率与储层剩余油饱和度之间的定量关系研究具有重要意义。

根据经典水驱油理论，产水率与含水饱和度之间满足Buckley-Leverett函数关系，在岩心相渗实验中，基于此可以获得含水饱和度与产水率之间的关系。由于实验所用原油黏度对结果影响较大，而在水驱油过程中地层原油的黏度受较多因素的影响，往往不是定值，因此实验结果在油田推广应用过程中往往效果较差。此外，对于非均质性储层而言，单一岩心实验结果往往代表性不强，且温度、压力、润湿性、孔隙结构等条件不能真实反映储层的渗流特征[6-7]。

本文基于注水油田丰富的生产动态测井资料，从油、水两相渗流理论入手，利用物质平衡方程及Welge方程，实现了水驱油藏剩余油饱和度的计算，并在油田实例应用过程中，基于Beta函数[8]建立了含水饱和度与产水率之间的定量转换关系式，以及驱油效率与产水率的定量关系，在指导油田水淹层水淹级别定量评价中应用效果显著。

1 剩余油饱和度计算新方法

1.1 基本原理

根据油水两相渗流理论，水驱油过程中存在三个区，即水区、油水混合区、油区(图1)，其中油水混合区将随着水驱的推进不断扩大，直到水驱前缘到达生产井排[9-10]。根据两相渗流理论等饱和度平面移动方程及大量实验与分析，当含油区内的束缚水饱和度为常数且原始的油、水界面与流线方向互相垂直时，位于油水两相区中的含水饱和度随位置的变化分布如图2所示[9-10]，图中Sw、So、Sor、Sof、Swf、Swc、Z分别为含水饱和度、含油饱和度、残余油饱和度、水驱前缘含油饱和度、水驱前缘含水饱和度、束缚水饱和度、可动油饱和度。

图1 水驱油含水非活塞式水驱油单向流模型[9-10]

图2 水驱油含水饱和度分布曲线[9-10]

(1)

其中，Qi、fw(Swe)满足以下关系[9-12]：

(2)

(3)

根据岩石体积物理模型[13](图3)及物质平衡原理，假设束缚水饱和度和残余油饱和度在水驱油过程中不会发生明显变化，则可动水体积与可动油体积满足

ΔVwm=-ΔVom

(4)

式(4)中：ΔVwm为可动水体积变化量，m3；ΔVom为可动油体积变化量，m3。

根据岩石体积物理模型，储层平均含水饱和度为束缚水饱和度与可动水饱和度之和，即

(5)

图3 岩石体积物理模型[13]

其中，可动水饱和度Swm可由物质平衡原理计算。

(6)

(7)

根据物质平衡原理，结合以上公式可以得到，水驱前缘剩余油饱和度满足：

So=1-Swi-Qor(t)-Qir(t)[fw(Swe)-1]

(8)

其中：

(9)

(10)

式(8)～(10)中：Qor(t)为累计产油相对体积，m3/m3；Qir(t)为累计注水相对体积，m3/m3；Qo,p为月产油量，m3/mon；Qw,p为月产水量，m3/mon。

1.2 利用时移生产动态测井资料计算剩余油饱和度

在剩余油饱和度计算公式(8)中，包含了束缚水饱和度、累计产油相对体积、累计注水相对体积和产水率4个参数，其中产水率可由生产动态测井直接测量获得，对于均质性地层束缚水饱和度相对为固定值，利用时移生产动态测井对关键参数累计产油相对体积和累计注水相对体积进行了计算。

A油田为一投产多年的注水开发油田，油田进入递减期。由于采用多层合采的生产方式，仅根据测试数据或者地面生产计量结果难以判断出水层位置，为了对油田实施动态监测，进行了大量的生产动态测井。A1井为2009年8月投产的一口生产井，X1小层发育稳定、分布范围广，束缚水饱和度和残余油饱和度分别为0.15、0.30。为了实现对产层的动态监测，2010年至2016年间累计进行了5次生产动态测井(表1)，常规测井及时移生产动态测井精细解释成果如图4所示。

表1 A1井X1小层时移生产动态测井解释成果Table 1 Interpretation results of time-lapse production performance logging in layer X1 of well A1

图4 A1井X1小层常规测井及时移生产动态测井解释成果图

基于前述理论结合表1中的实际测量数据，可以得到产油量与生产时间的关系(图5)、累计产油量与产油量关系(图6)。根据图6及式(7)、(8)可以得到无水原油饱和体积及相应的含水饱和度、剩余油饱和度(表2)。根据油田现场经验，通常在油田开发后期使用Arps递减方程来预测原油产量及确定可采储量[14-23]，通过对时移生产动态测井资料计算的产量关系分析，该产量递减类型符合指数递减。

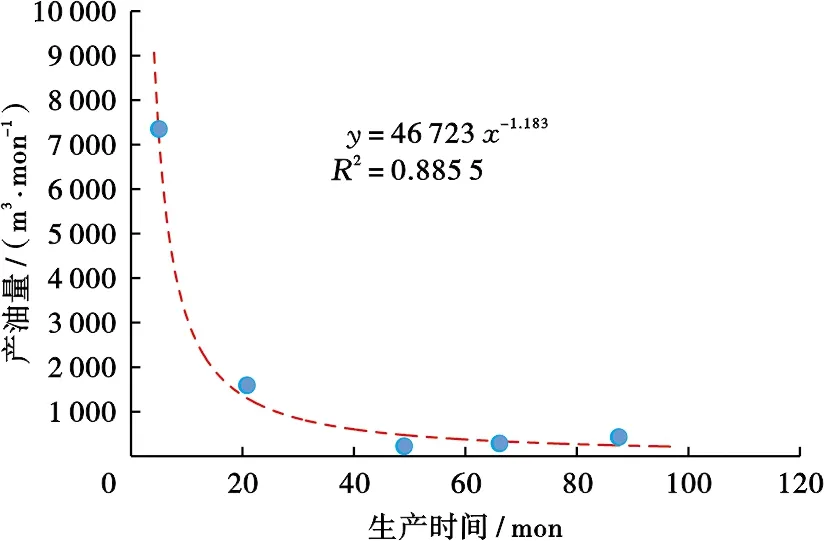
图5 X1小层产油量变化图

图6 X1小层累计产油量与产油量关系图Fig .6 Relationship between cumulative oil production and reduced oil production of layer X1

表2 A1井X1小层参数计算结果Table 2 Calculation results of X1 sub layer parameters in well A1

2 在水淹层评价中的应用

由表2得到产水率与含水饱和度的交会关系，根据产水率与含水饱和度的分布范围和特征，利用不完全Beta函数进行曲线拟合，通过迭代算法找到全局最优解，得到产水率与含水饱和度之间的不完全贝塔函数关系为

(11)

X1小层产水率与含水饱和度关系如图7所示，可以看出，拟合曲线与岩心实验数据曲线形态相似，在含水饱和度高于0.55时，两者差异较小，在含水饱和度低于0.55时，两者差异较大，即含水饱和度增加时拟合曲线的产水率上升更快。分析认为，地层孔隙结构复杂、非均质性强，岩心实验难以反映产层的整体渗流特征；本次研究以小层为计算单元，能更好地反映地层的实际生产情况。

图7 X1小层产水率-含水饱和度关系图

利用本文方法对储层进行产水率计算及水淹级别定量划分，综合解释成果如图8所示。选取产量、产水率变化不大、生产动态测井时间与裸眼井测井时间间隔较小、未发生措施变更的井进行验证。

在水淹级别解释的过程中，首先基于裸眼井测井开展水淹层定性解释，然后对裸眼井测井定性解释的水淹层进行产水率定量计算，根据油田水淹级别划分标准可以实现水淹级别的有效划分(图8)。可以看出，利用本文模型解释的水淹级别与检验井生产动态测井水淹级别整体符合性较好，仅在1 800.0～1 803.5 m小层模型解释未水淹，生产动态测井解释为强水淹，从常规测井电阻率曲线可以看出，裸眼测井时1 800.0～1 803.5 m小层电阻率大于30.0 Ω·m，为典型的油层特征，而生产动态测井曲线显示该小层为明显的水层，造成这一结果的原因在于尽管生产动态测井与裸眼井测井时间较为接近，但该井水淹推进较快，油层很快水淹所致。

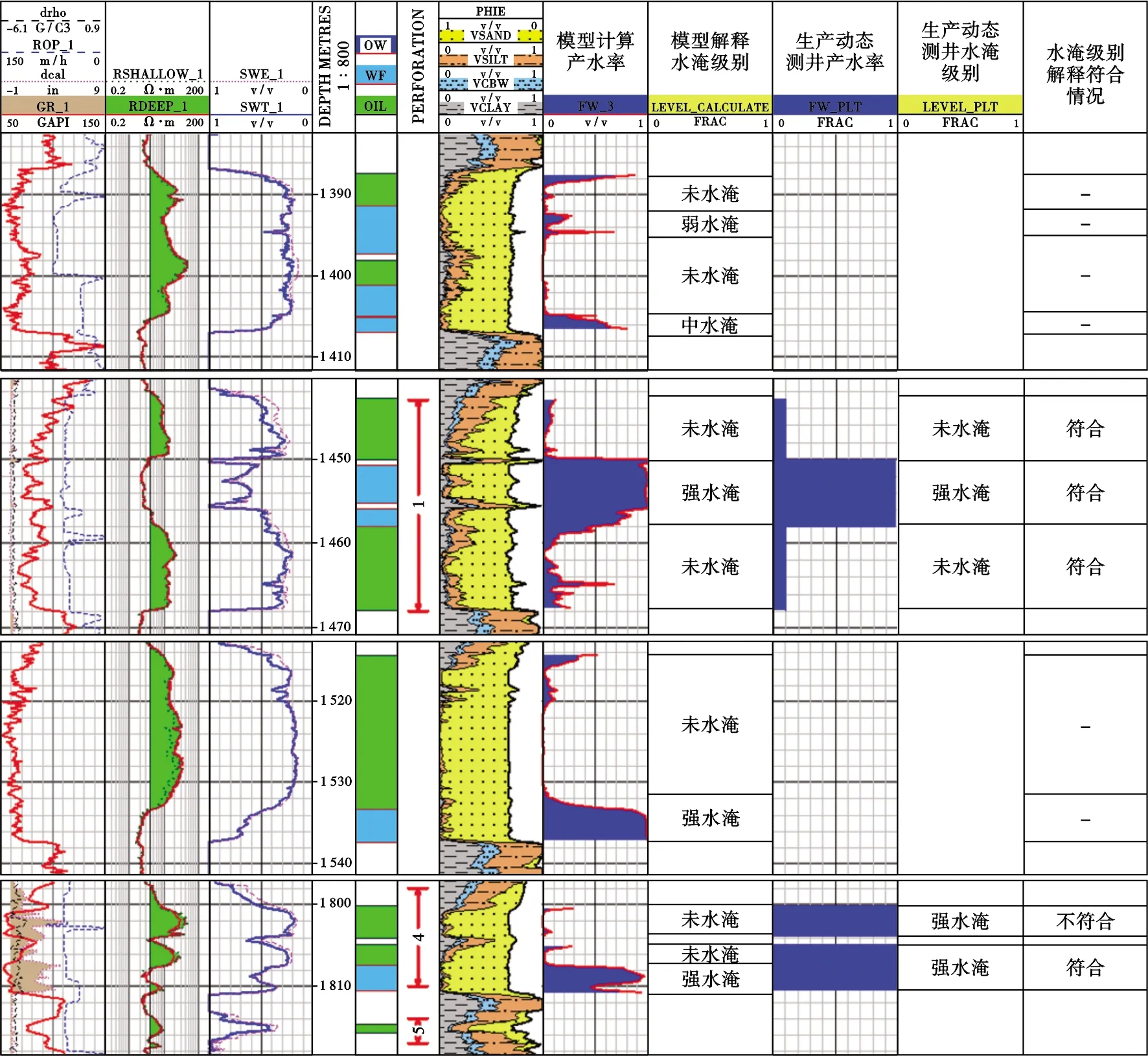
图8 水淹级别定量划分成果图

由于不同物性的储层束缚水饱和度、残余油饱和度存在较大差异，因此利用产水率与含水饱和度的关系进行水淹级别的判别仅可用于同一类型的储层，难以推广应用到其他储层类型。大量研究表明不同类型储层的驱油效率与产水率之间关系基本一致，因此笔者进一步建立了驱油效率与产水率之间的关系(图9)以实现上述方法的推广应用，获得水淹层水淹级别划分标准(表3)，其中驱油效率计算公式[13]如下：

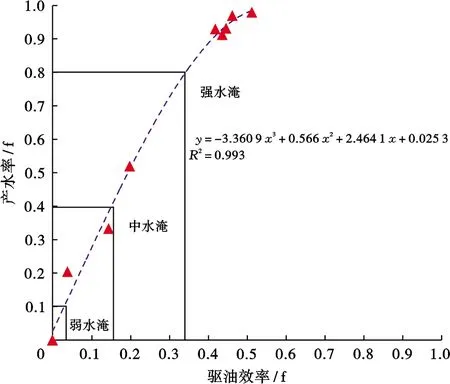
图9 A油田产水率-驱油效率关系图Fig .9 Relationship between water production rate and oil displacement efficiency in A oilfield

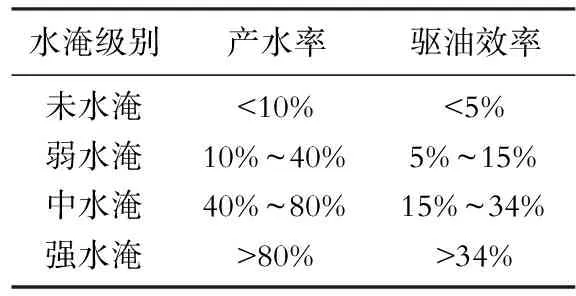
表3 A油田水淹级别判别标准Table 3 Standard of water flooded level in A oilfield

(12)

式(12)中：ED为驱油效率，f；Sw为含水饱和度，f；Swi为束缚水饱和度，f。

图10为基于驱油效率的水淹级别定量划分成果。在驱油效率的基础上根据图9中产水率与驱油效率的关系式计算得到了产水率FWZ，该井进行生产动态测井的时间与裸眼井测井时间相近，且此时间段内未发生生产措施变化、地面产量稳定，因此生产动态测井能够真实的反映裸眼井的产出状况。从图10可以看出，在20个小层的水淹级别划分中，18个层符合，符合率高达90%。分析其中两个不符合的层均为层厚小于2.0 m的III类层，此类层物性条件差、产量贡献极低，生产动态测井和裸眼测井解释均存在一定的误差，从而造成水淹级别划分的结果与生产动态测井相矛盾。而在物性较好的I类层(层厚大于5.0 m)和II类层(层厚大于2.0 m，小于5.0 m)中，水淹级别划分的符合率较高。