基于叠加式传感器的多普勒雷达多目标联合检测与估计

董文豪 达凯 宋志勇 付强

（国防科技大学电子科学学院ATR国防重点实验室，湖南长沙 410073）

1 引言

多普勒雷达通过多普勒效应来探测目标的位置和相对速度，广泛应用在机载预警、导弹制导、战场侦察和天气预警等领域中，在强杂波背景和一些干扰的情况下也可实现对目标的探测［1］。随着隐身技术的不断发展，目标雷达散射截面积（Radar Cross Section，RCS）呈数量级递减趋势，低信噪比（Signal-to-Noise Ratio，SNR）下的多目标检测与状态估计成为了多普勒雷达发展中的基本任务和重大挑战［2］。

传统的多目标检测估计方法为跟踪前检测（Detect Before Track，DBT），在一定的虚警率下，基于Newman-Pearson 准则利用目标与背景间的能量差异来得到目标检测结果。基于数据的传统多目标跟踪方法主要有联合概率数据关联（Joint Proba⁃bilistic Data Association，JPDA）［3］和多假设跟踪（Multi-Hypothesis Tracking，MHT）［4］，低SNR 情况下需要降低判决门限来保留目标信息，确保目标通过门限的同时也带来了大量虚警，这类方法由于数据关联导致计算复杂度过高而难以有效检测和估计目标。Mahler 开创的有限集统计学理论（Finite Set Statistics，FISST）可有效避免数据关联，利用随机有限集（Random Finite Set，RFS）描述多目标状态和量测，与贝叶斯框架完美融合，发展出的多目标跟踪方法有概率假设密度（Probability Hypothesis Den⁃sity，PHD）［5］、集势概率假设密度（Cardinalized PHD，CPHD）［6］和多伯努利滤波器（Multi-Bernoulli，MBR）［7］。PHD 滤波器假定分布为多目标泊松过程，通过一阶矩近似可完全描述多目标分布，CPHD滤波器假定分布为独立同分布群过程（Independent and Identically Distributed Cluster，IIDC），通过二阶矩近似可同时传播势分布和PHD，与PHD滤波器相比准确估计目标数目的同时也增加了计算复杂度。PHD 和CPHD 滤波器都使用单个密度函数来表示多个单目标状态，MBR 滤波器使用多个伯努利RFS对多目标状态建模，每一个伯努利项利用存在概率和状态密度函数来表示。针对MBR 滤波器的势偏置问题，Vo［8］提出了势均衡多伯努利滤波器（Cardi⁃nality Balanced Multi-target Multi-Bernoulli，CBMeM⁃Ber）。为了形成目标轨迹，Vo［9］提出了广义标签多伯努利（Generalized Labeled Multi-Bernoulli，GLMB）的可计算近似解，简化了计算量。FISST 在多传感器多目标跟踪领域也有新的发展，文献［10］通过得到所有目标轨迹的概率分布来解决GLMB多传感器多目标场景中的轨迹断裂问题，有关多传感器的最新研究进展可参考文献［11］。

以上的RFS 滤波器文献都是基于标准传感器，标准传感器是指一个目标只能产生一个量测结果或者不产生量测，且每个量测只能由单个目标或者背景产生。叠加式传感器是指每个量测都以叠加的方式受到多个目标影响，即多个目标对测量的贡献等于单独每个目标单独存在时对量测的贡献之和，且每个目标可以影响任意数目的量测，因此量测之间不独立。多普勒雷达回波信号为各个目标产生的多普勒回波叠加形成的时域信号，通过对时域回波的分析处理来判断是否存在目标并估计出其多普勒频率、幅相特征，属于典型的叠加式传感器应用。除此之外，叠加式传感器的应用场景有阵列天线到达角（Direction of Arrival，DOA）估计［12］、无线通信网络多用户检测［13］、射频层分析跟踪［14］和基于热源定位的热电堆阵列［15］等。基于叠加式传感器的多目标RFS 滤波器在预测步骤与基于叠加式传感器的经典多目标RFS 滤波器相同，都是把多目标状态建模为RFS，而两种滤波器的更新步骤不同，前者把量测建模为随机矢量，而后者把量测建模为RFS。马勒推导了一般叠加式CPHD 的精确滤波方程［16］，但该方程由于计算复杂而难以实现。针对该问题，Hauschildt 提出了一种近似闭式解［15］，但也只适用于少量密集目标情形。Thouin、Nannuru和Coates于2011年提出了加性似然矩（additive like⁃lihood Moment，ALM）滤波器用于叠加式PHD 滤波器递推，该近似方法有效但其中的观测更新方程只适用于离散状态空间，马勒在此基础上推广得到了近似叠加式CPHD滤波器［17］，随后与Nannuru 与Coates 汇总了该滤波器及其特例（即PHD 滤波器），并给出了可计算处理的近似叠加式PHD 和叠加式CPHD 的辅助粒子实现形式［18］。叠加式RFS传感器在MBR 滤波器也得到了发展，与叠加式CPHD 滤波器的推导方法类似，Nannuru 和Coates 通过为每一个伯努利RFS 定义一个条件PHD，然后在用与叠加式CPHD 滤波器类似的推导方法来推导叠加式MBR滤波器［19］，并给出了其粒子实现形式［20］。考虑到CPHD 滤波器中的势分布可准确估计目标数目，Nannuru 和Coates 推导了混合叠加MBR 和CPHD 滤波器的更新方程及辅助粒子实现，验证了该滤波器在模拟声学传感器和射频层分析中的有效性［21］。国内基于叠加式传感器的RFS 多目标滤波器研究较少，范红旗的译著［22］第19 章介绍了部分相关进展，但至今还没有将其应用到多普勒雷达目标检测估计领域的相关文献。

IIDC RFS 仅使用一个状态密度函数对所有目标进行建模，而MBR RFS可单独对每个目标建模并更新其状态信息，MBR RFS 不仅结果简单，而且更适合处理极端非线性情况，但其缺点是目标数目估计精度不如IIDC RFS 准确。此外，由于目标数量随着时间的推移而变化，MBR 滤波器由于需要在每个时间步添加多个伯努利分量来对新生目标建模而导致计算效率较低，使用IIDC RFS 对新生目标建模，只有在新生目标出现时才会导致IIDC RFS 执行聚类操作，其他情况则不需要执行复杂度较高的聚类操作。综合以上因素，本文将多普勒雷达回波信号建模为叠加式传感器模型，考虑使用混合MBRCPHD 滤波器，给出了贝叶斯框架下该滤波器的预测和更新方程，并基于辅助粒子滤波方式实现了多普勒雷达多目标的联合检测与状态估计。具体内容安排如下：首先描述了目标状态RFS 和观测随机矢量，紧接着分别介绍了MBR RFS 和IIDC RFS，以及混合MBR-CPHD 滤波器的预测方程和更新方程。然后给出了该滤波器的辅助粒子滤波实现步骤，并对多普勒雷达回波信号仿真，验证滤波器的有效性。最后对全文进行总结。

2 问题描述

2.1 状态RFS

多普勒雷达回波信号的一般形式如下：

其中，a为信号幅度，f为由雷达平台和目标径向运动引起的多普勒频率，φ为信号初始相位，单目标状态矢量可用向量x=[φ，f，a]T表示，k时刻目标状态RFS 可表示为，Nk≥0 表示k时刻的目标数目，单目标相位和频率关系与距离和速度关系类似，可由CV 模型来描述，因此相位和频率关系可表示为：

其中，λ=c/f0为载频波长，c为光速，f0为载波频率，噪声ωc为有目标径向加速度引起的零均值高斯白噪声，ωc∼Ν(0，)。

假定目标幅度不变，即目标为非起伏目标，采用一阶AR模型来描述非起伏目标：

其中ωa是零均值高斯白噪声，分布为ωa∼Ν(0，)，则状态转移模型表示为：

2.2 观测随机矢量

k时刻的观测矢量可表示为Zk=[zk，1，zk，2，…，]，对于多普勒回波信号，其观测模型为：

其中，观测噪声vk为独立的复高斯矢量，其概率密度函数如下：

其中fs为信号采样频率，则似然函数可表示为：

3 随机有限集

3.1 MBR RFS

单目标伯努利的PHD为：

MBR RFS是N个统计独立的单目标伯努利RFS 的并集，即Ξ=Ξ1∪Ξ2∪...∪ΞN，则多目标伯努利RFS的PHD为［7］：

3.2 IIDC RFS

IIDC RFS 用势分布πc(n)和密度函数qc(x)表示，IIDC的PHD表示为：

其中μc是势分布均值，对应的二阶矩分别为［17］：

3.3 混合MBR-CPHD滤波器

考虑到MBR 滤波器结构简单，且适用于式（7）这种极端非线性观测模型，而CPHD 滤波器的势分布可以用来准确估计目标数目，因此采用混合MBR-CPHD 滤波器基于贝叶斯准则实现多普勒雷达多目标联合检测与估计，具体步骤如下。

预测

将k时刻的后验分布建模为MBR RFS，参数表示为：

更新

更新步骤基于贝叶斯规则传播三个参量，分别为：MBR 分量的PHD、IIDC 分量的PHD 以及IIDC 分量的势分布，具体表示为：

式（22）至式（25）的推导可参考文献［17］和文献［18］。

IIDC分量的PHD更新为：

式（29）和式（30）的推导可参考文献［17］和文献［18］。

IIDC分量的势更新为：

式（33）和式（34）的推导参考文献［17］和文献［18］。可以认为MBR 滤波器是混合MBR-CPHD 滤波器的特例，通过将混合MBR-CPHD 滤波器中的IIDC 分量置为空集即可得到MBR滤波器。

4 MBR-CPHD辅助粒子滤波实现

由于式（7）的高度非线性，混合MBR-CPHD 滤波器需采用粒子实现形式。粒子滤波器首先需要设计重要性分布（也叫提议分布）进行粒子采样，粒子滤波器的经典代表自举（Boot-Strap）滤波器就是把状态转移函数作为重要性分布，由于没有考虑观测值，可能导致该滤波器的提议分布与似然分布差别较大，只有极个别采样粒子位于高似然区，进而引起粒子退化问题。为此，我们采用辅助粒子滤波器（Auxiliary Particle Filter，APF）［23］，利用观测值构建辅助变量，在此基础上设计提议分布可以增加高似然区域内的采样粒子数，具体实现步骤如下。

步骤1 提议分布设置：

设辅助分布为：

步骤2 预测：

对于存活目标，对应RFS 为MBR 分量，基于状态转移密度对粒子状态进行预测，即

MBR分量的存在概率预测为：

对于新生目标，对应RFS 为IIDC 分量，粒子在状态空间中均匀采样，势分布为离散的均匀分布。

步骤3 更新：

对粒子权重进行更新：

步骤4 IIDC RFS近似及重采样

由于使用伯努利随机有限集更好地表示单个目标，因此使用多个伯努利分量近似更新的IIDC分量，最终的后验分布使用MBR RFS建模。先利用最大似然估计器估计出IIDC 分量中最大势，然后利用K 均值算法对IIDC 分量进行聚类，将其划分为Nck+1个存在概率为1 的伯努利分量，然后对所有的MBR分量重采样，即

步骤5 航迹管理

设置存在概率门限τ，当MBR 分量中的第i个存在概率若满足

则删除第i个伯努利项，反之则保留作为存活目标RFS。

5 仿真

多普勒雷达信号的基本参数设置如表1所示。

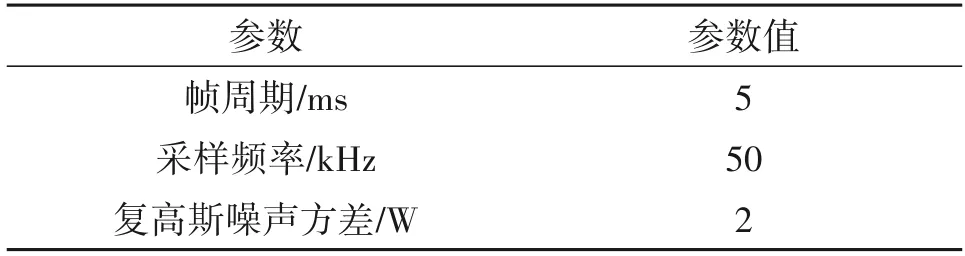
表1 仿真参数Tab.1 Simulation parameters

仿真时长为50 帧，每一帧的观测矢量维度为L=5ms×50kHz=250，观测噪声协方差矩阵∑z=2 ⋅IL×L，共设置三个目标，目标1始终存在，目标2在第9帧出现，第35帧消失，目标3在第17帧出现，第24 帧消失。混合MBR-CPHD 滤波器的最大目标数设为15，每个目标粒子数为1000，粒子存活概率和新生概率分别设置为0.9、0.1，且均与粒子状态无关，过程噪声方差设置为σc=0.5，σa=0.5，存在概率门限设为τ=0.1。

当信噪比为-4 dB 时，MBR 滤波器和混合MBR-CPHD 滤波器的单次运行结果如图1 至图4所示。

从图1 至图3 可以看出，三个目标的相位在中间时刻相互交叉，即使目标相位在仿真时间段内不断跳变，MBR 滤波器和混合MBR-CPHD 滤波器几乎都能准确估计出不同时刻不同目标的真实相位；由于假设状态模型为CV 模型，所以不同目标频率保持不变，三个目标的信号幅度相同，MBR 滤波器和混合MBR-CPHD 滤波器也都可以较为准确地估计出目标的真实频率和真实幅度，但MBR滤波器存在一定的延迟效应，前两次目标新生时MBR滤波器会延迟1～3 帧。这是由于CPHD 可以通过势分布准确估计出目标数目，所以混合MBR-CPHD 滤波器可以准确估计目标新生和消失，并准确估计出对应的目标状态，正如图4所示。

为了有效评估RFS 多目标滤波器的状态估计精度与目标数目估计精度，采用最优子模式分配度量（Optimal Sub Pattern Assignment，OSPA）［7］作为性能评价指标，其中的势代价因子c决定目标数目估计精度相对于相对状态估计精度的重要性，灵敏度因子p决定滤波器对虚警或者漏检的敏感度。由于目标状态变量量纲不同，单独统计不同信噪比下不同目标状态的OSPA，分别做100 次蒙特卡洛实验，结果分别如图5 至图7 所示。随着信噪比的提高，MBR 滤波器和混合MBR-CPHD 的性能都有所提升，但混合MBR-CPHD 滤波器对每一个目标状态变量的估计性能几乎都优于MBR滤波器，仅当信噪比为1 dB 时MBR-CPHD 滤波器的频率OSPA 统计值略高于MBR 滤波器，可能原因是本身MBR 滤波器相比CPHD 滤波器更适用于本文高度非线性应用，随着信噪比的提高，导致混合MBR-CPHD 的估计性能改善略低于MBR滤波器。从整体对比发现，MBR滤波器受信噪比影响更大，当信噪比为-4 dB 时，其各个状态变量的OSPA 距离均远大于混合MBRCPHD滤波器。

为了比较MBR 滤波器和混合MBR-CPHD 滤波器的计算复杂度，进行100次蒙特卡洛实验，统计每次蒙特卡洛试验的执行时间直方图对比如图8 所示。MBR 滤波器中的新生步骤由于需要多个伯努利项实现，导致MBR 分量计算复杂度提高，CPHD滤波器中的粒子聚类步骤同样也需要大量的计算，但混合MBR-CPHD 滤波器中只有在目标新生时才会有聚类步骤，当目标数目不变或者消亡时不需要执行此步骤，而MBR 滤波器时刻需要执行新生步骤，因此混合MBR-CPHD 滤波器的执行时间小于MBR滤波器。

6 结论

为了避免低信噪比下的目标信息丢失，本文直接基于原始多普勒雷达回波信号并将其建模为叠加式传感器模型，利用混合MBR-CPHD 滤波器估计多普勒雷达多目标的个数及其状态，并给出了该滤波器的APF 实现流程。仿真实验结果表明，与基于叠加式传感器的MBR 滤波器相比，混合MBR-CPHD 滤波器在低信噪比下的目标数目和状态估计精度更高，同时降低了计算复杂度。