面波频散能量谱计算方法
2022-06-23于涵,刘财,王典,鹿琪
于 涵,刘 财,王 典,鹿 琪
吉林大学地球探测科学与技术学院,长春 130026
0 引言
浅层地震勘探的目的在于确定较小尺度下地质体的结构特征和地质剖面的物性参数,对解决浅层地质问题、探测浅层地下空间具有重要意义[1-3]。面波勘探为无损性浅表地震勘探,以面波的频散特性为基础。不同周期的面波以不同的波速进行传播。周期越长的面波其纵向传播距离越远,越能反映较深处地下介质的响应特征。通过测量不同周期的面波速度,可以得到面波中不同频率成分对应速度的关系(即频散曲线),这样的频率-速度关系受到地下介质的影响[4-5]。采取合理的数据处理方法,有效提取面波频散曲线,是提升面波勘探精度的重要手段[6-9]。通过构建相应的反问题,利用反演方法可以推断地下不同深度介质的属性,从而达到工程勘探的目的[10-11]。
19世纪中期,英国物理学家Rayleigh[12]研究发现一种P波(纵波)与SV波(垂直偏振横波)在自由表面干涉形成并沿自由表面传播的Rayleigh波,对其产生的数学物理机理进行了论述。Love[13]从数学上证明了Love面波的存在。Thomson[14]、Haskell[15]发现了多层介质中Rayleigh波的频散特性。受限于当时的计算能力,并未在实验中得到充分验证。随着计算水平不断的提升,面波的理论研究得到了快速的发展。Aki[16]通过地震噪声源得到地下面波的频散信息,首次利用噪声源获取面波信息。von Seggern等[17]从地震爆炸谱比角度,分析Rayleigh波层状介质传递函数对源谱的影响,定义了Rayleigh波。Campillo等[18]对两个地震台站记录的地震尾波进行了互相关处理,从互相关函数中识别出了Rayleigh波和Love波的信号,证明随机波场具有频散性质。同年,Hayashi 等[19]运用互相关方法从背景噪声中提取出面波数据。Park等[20]在主被动源激发的地震数据中有效提取面波信息,在近地表速度成像方面取得了良好的应用效果。
频散能量谱主要计算方法有:τ-p变换法(τ为垂直波慢度,p为水平波慢度)、高分辨率线性Radon变换法、频率分解法、相移法、f-k变换法(f为频率,k为波数)、SFK(slantf-k)变换法和矢量波数变换法等。Mcmechan等[21]最早提出τ-p变换计算方法,将离散波列的线性Radon变换方法应用到Rayleigh波地震波场分离中。许多学者针对τ-p变换法的地震数据处理效果进行了进一步研究,针对端点效应和假频效应等问题提出了改进方法,并取得了较好的效果[22-25]。Luo等[26]在线性Radon变换中引入加权系数,提出高分辨率线性Radon变换法。Xia等[27]提出了利用拉伸函数与地震数据褶积形成频率扫描数据,之后进行倾斜叠加变换的频率分解法。Park等[28]基于面波的相位信息进行倾斜叠加,加大了对相位信息的探索,抑制了空间假频,增强了频散能量谱上的相干信号,提高了频散能量谱的分辨率,提出相移法求取瞬态Rayleigh面波频散能量谱。伍敦仕等[29]和Cheng等[30]提出改进的相移法成像方法,一定程度抑制了空间假频的干扰,并增强了频散能量谱上的相干信号,提高了频散能量谱的分辨率。Gabriels等[31]利用f-k变换提取出Rayleigh波频散曲线。Serdyukov等[32]利用S变换改进了f-k变换,在时频域自适应调解时窗函数,显著放大面波信息,增强了频散能量谱的低频有效信号,提高了频散能量谱的抗噪性,有效抑制空间假频现象,称之为SFK变换。杨振涛等[33]提出了矢量波数变换方法,在f-k变换法基础上引入地震矩张量概念,提供了更丰富的高阶模态面波频散信息。近年来,大量学者结合先进的信号处理方法,利用不同的时频分析方法扩展波束形成能力,选择最佳观测时窗提高识别时空上传播波的灵活性以及方法的分辨率,进一步提高了面波的成像精度和成像质量,并验证了其高效性和较好的应用潜力[34-39]。
本文分析了τ-p变换法、高分辨率线性Radon变换法、频率分解法、相移法、f-k变换法、SFK变换法和矢量波数变换法等7种频散能量谱成像方法的技术原理和特点,通过对理论模型合成的Rayleigh波记录进行处理,比较了不同方法在f-v(速度)域频散能量谱的成像效果,并对各方法的优缺点进行了总结。
1 计算方法理论基础
1.1 τ-p变换法
τ-p变换法又称离散线性Radon变换法。用τ-p变换法求取频散曲线,实质上是一种由两个线性变换组成平面波的分解方法[17]。
将共炮点面波地震数据h(x,t)进行τ-p变换,沿直线方程t=τ+p进行倾斜叠加,其离散形式表示为
(1)
式中:τ为垂直波慢度;p为水平波慢度;x为偏移距;xmax、xmin分别为x的最大值和最小值;t为时间。式(1)沿时间方向进行一维傅里叶变换得
(2)
式中,U(f,p)和H(x,f)分别为u(p,τ)和h(x,t)的一维傅里叶表现形式。根据v=1/p,得
(3)
实际数据处理过程如下:
其中:①对h(x,t)沿不同斜率的直线方程进行积分,得到u(τ,p);②沿时间方向做一维傅里叶变换,得到U(f,p);③转换至频率速度域。
1.2 高分辨率线性Radon变换法
高分辨率线性Radon变换在Radon变换的基础上引入加权函数,用于降低含噪数据对频散能量谱成像效果的限制。
式(2)τ-p反变换的离散形式可以表示为
(4)
式中:pmax、pmin`分别为p的最大值和最小值。式(4)写为矩阵形式为
H=LU。
(5)
式中:H为数据空间向量;U为模型空间向量;L为线性Radon变换算子矩阵。类似地,式(3)也可写成矩阵形式:
U=LTH。
(6)
通过预加权的共轭梯度算法降低面波数据中的噪声限制,提高分辨率。在方程(5)中引入模型权重矩阵Wu,得
(7)
反演过程中引入阻尼因子λ,得
U=(LTL+λI)-1LTH。
(8)
算法核心是求取目标函数最小解,求得U。目标函数M表示为
(9)
对式(9)中的U求导并令导数为零可得
(10)
式中:I为单位矩阵;Wh为数据权重矩阵。可通过共轭梯度法求解式(10)[26]。
实际数据处理过程如下:
其中:①对h(x,t)沿时间方向做一维傅里叶变换,得到H(x,f);②对H(x,f)进行高分辨率线性Radon变换,沿不同斜率的直线方程进行倾斜叠加,得到U(f,p);③转换至频率速度域。
1.3 频率分解法
频率分解法是基于τ-p变换原理的改进方法,通过褶积计算,将时间域转换至频率域,将原始地震数据转换为连续频率下的地震数据,并对其进行类似τ-p变换法的倾斜叠加变换,从而得到频散能量谱。
对h(x,t)进行褶积:
Hr(x,t)=r(t)⊗h(x,t) 。
(11)
其中:
(12)
式中:Hr(x,t)为瞬时频率地震记录;r(t)为扫描样本函数;f(t)为时间与频率一一对应的瞬时函数。
实际数据处理过程如下:
其中:①对h(x,t)进行褶积,生成Hr(x,t);②对Hr(x,t)进行τ-p变换(具体处理过程如1.1节),转换至频率速度域。
1.4 相移法
相移法本质是在频率域内对相位信息进行倾斜叠加,是目前主动源面波频散成像应用最广泛的一项技术。
对h(x,t)沿时间方向做一维傅里叶变换,得

(13)
将式(13)表示为相位谱与振幅谱的乘积:
H(x,f)=P(x,f)A(x,f)。
(14)
式中:P(x,f)为相位谱,包含了频散的所有信息;A(x,f)为振幅谱,包含了地震信号的其他信息,如振幅衰减、球面扩散等。
基于频散特性,面波数据可表示为
U(k,f)=cos(2πft+2πkx+φ0)。
(15)
式中,φ0为初始相位。相位谱2πkx+φ0表示各频率简谐波在时间原点的相位,与偏移距相关。将相位谱用e-iΦx表示,则式(14)可表示为
H(x,f)=e-iΦx+φ0A(x,f)。
(16)
其中:
式中,vf为不同频率对应的相速度。
对同一频率面波的各相位信息进行空间积分,得
(17)

实际数据处理过程如下:
其中:①对h(x,t)沿时间方向进行傅里叶变换,得到H(x,f);②归一化频谱,消除振幅谱影响,对各道地震波能量谱沿着空间水平方向叠加求和,得到U(φ,f);③根据频率与相位之间的关系,转换至频率速度域。
1.5 f-k变换法
f-k变换法的本质是对面波的频散特征进行二维傅里叶积分变换。
对h(x,t)沿时间方向做一维傅里叶变换后(式(13)),沿空间方向做一维傅里叶变换,得

(18)
根据v=f/k,即可得到频率速度域频散能量谱U(f,v)。
实际数据处理过程如下:

1.6 SFK变换法
近年来时频分析方法已广泛应用于主动源和被动源面波频散成像中,核心在于时频变换窗函数的选取,在不同尺度下对面波信号进行分析,从而有效地提取面波频散信息。时频分析方法目前有很多种,本文仅详细介绍基于S变换改进的f-k变换。
对第一道地震数据h1(t)进行S变换:
S[h1(t)](τ,f)=
(19)
式中,τ为时间轴上高斯窗的分析点位置。第二道数据h2(t)可以用h1(t)表达:
S[h2(t)](τ,f)=
(20)
e-i2πk(f)le-ζ(f)lS[h1(t)]](τ-k′(f)l,f)。
式中:ζ(f)为与频率相关的衰减参数;k(f)为与频率相关的波数,k′(f)为k(f)的频率导数;l为两道数据之间的距离。将S变换应用于地震记录中,形成同一频率的伪面波地震记录:
hf(x,τ)=S[h(x,t)](τ,f,x)。
(21)
式中,hf(x,τ)为S变换后的共频率伪面波记录。
假设震源在零时间产生一个冲量和偏移量,引入基于S变换的面波分组模型[35]:
(22)

(23)
式中,μf(x,τ)为误差项,包含其他地震波、噪声和建模图像误差。
固定时间、频率,在群速度范围内对伪面波地震记录进行倾斜切片,式(21)可表示为
(24)
式中,huf(x)为倾斜相位函数。再沿x方向做傅里叶变换,得
(25)
寻找群速度最大振幅:

(26)
实际数据处理过程如下:
其中:①对h(x,t)进行S变换生成hf(x,τ);②将hf(x,τ)固定时间、频率,在群速度范围内进行倾斜切片,得到huf(x);③沿时间方向进行傅里叶变换并取极大值得到U(f,k),转换至频率速度域。
1.7 矢量波数变换法
杨振涛等[33]近年来在f-k变换法的基础上,研究垂直于地面单力点源产生的地震,基于不同阶贝塞尔函数对应的实部与虚部频散谱不同,以波数维度对称性为核心思想,引入地震矩张量概念,对f-k变化进行优化。
在地表面观测到的垂直分量地震波场记录可表示为
h(x,t)=f(t)*g(x,t)。
(27)
式中,g(x,t)为震源与观测点间的格林函数。对式(27)进行傅里叶变换,得
H(x,ω)=F(ω)G(r,ω)。
(28)
式中:G(r,ω)为震源与观测点间在频率域的格林函数;r=|x|;ω为角频率。自由表面各向同性震源的格林函数在频率域的计算公式可以表示为

(29)
式中:g(ω,k)为格林核函数;J0(kr)是第一类零阶贝塞尔函数。
(30)
式中,θ为方位角。
对观测波场的频谱进行矢量波数变换[33]:
(31)
当空间为水平层状介质时,矢量波数变换结果仅依赖波数矢量的模k(k=|k|),与波数矢量的方向无关,式(31)可以表示为

(32)
在频率域中式(32)可以表示为

(33)
根据贝塞尔函数的正交性[40]:
(34)
将式(34)代入式(33),简化为

(35)
g(ω,k)与面波频散特性的久期函数值成反比,矢量波数变换依据此特性进行频散能量谱计算。
根据v=ω/k、ω=2πf/v,可以得到频率速度域频散能量谱U(f,v)。
实际数据处理过程如下:
其中:①对h(x,t)沿时间方向进行傅里叶变换转换至频率域,得到H(r,ω);②对H(r,ω)进行多道地震数据加权求和,根据式(35)获得g(ω,k);③对g(ω,k)进行相速度和波数扫描,获得近似格林核函数图,根据速度、频率和波数之间的关系,转换至频率速度域。
2 频散能量谱效果对比
本文建立了三层速度递增水平层状介质模型(表1),震源为主频20 Hz、延迟时间0.03 s的高斯子波,将其布置在(10 m, 0 m)处。图1a为模型合成的Rayleigh波地震记录,最小偏移距是5 m,道间距为2 m,每道的采样点数为6 000,采样时间间隔为0.2 ms,记录延续时间为1.2 s。由图1a可见,利用该模型模拟的60道Rayleigh波地震记录(垂直分量)清晰可见,发散的扫帚状十分明显。利用此合成记录,应用上文所述7种方法变换得到频散能量谱,并与多模式快速矢量传递算法求取的理论频散曲线[41](频率为5~100 Hz,间隔1 Hz)进行对比,结果如图1b—h所示。
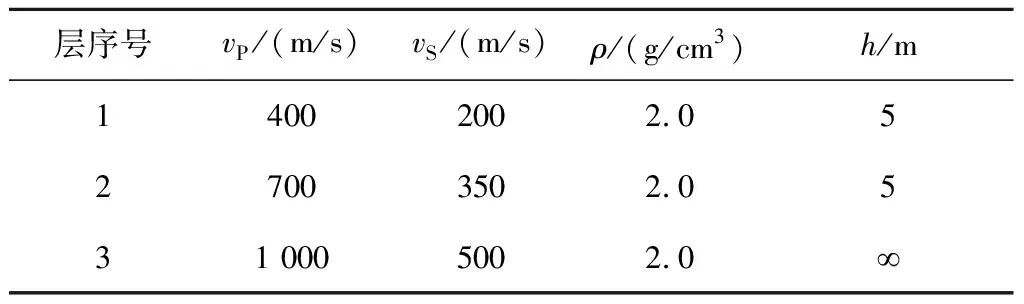
表1 三层速度递增水平层状介质模型参数
由图1可见,文中所述7种方法均可对面波频谱有效成像,对于基阶面波频散曲线变化趋势具有相似的特征,识别效果均较为清晰。f-k变换法在频率20 Hz以内频散能量谱极值点与解析解误差较大, 低频成像精度低,高阶模态频散能量信息不明显;由于速度与波数之间的映射关系,矢量波数变换法和f-k变换法存在明显的空间假频现象,可能由于计算过程中插值不均导致;频率分解法在15 Hz以内的频散曲线存在明显波动,能量较为丰富;对于多模态下的面波频散信息,f-k变换法无法有效拾取高阶面波频散曲线,频率分解法、矢量波数变换法、相移法、高分辨率线性Radon变换法频散能量谱分辨率较高,可有效提取出高阶面波频散曲线。

a. 合成Rayleigh波地震记录。频散能量谱:b. τ-p变换法;c. 高分辨率线性Radon变换法;d. 频率分解法;e. 相移法;f. f-k变换法;g. SFK变换法;h. 矢量波数变换法。图中白点为频散曲线的解析解。
对文中7种方法的计算耗时进行比较,结果如表2所示。由表2可见,f-k变换法计算速度最快,频率分解法、矢量波数变换法和SFK变换法计算速度较慢。
近年来,各种频散能量谱计算方法已经在面波工程勘探领域广泛应用。多种面波勘探方法,如共中心点互相关二维面波法、瞬态多道面波分析法和面波谱分析法等已被国内外多家生产和科研单位使用,在工程勘探中也有深入探讨[42-47],面波勘探技术已在近地表地质勘察、石油勘探、隧道检测和大坝稳定性等实际应用中取得良好效果[48-53]。本文针对不同面波勘探方法适用的地质环境、采集方式和适用空间范围等方面进行整理,结果如表3所示。文中详细阐述的7种数据计算方法,多应用于主动源及被动源面波勘探二维多道采集数据处理过程中。近年来,许多学者应用不同频散能量谱计算方法对实际数据进行了处理[54-60],本文对其应用特点进行总结。
τ-p变换法:计算量小、失真小、易于实现、压制端点效应好,对多阶模态面波频散信息成像效果较好;但对基阶模态低频面波频散信息的成像效果较差,会出现波场能量延伸和假频现象,结果易导致反变换后的波场相互叠加干涉。

表2 频散能量谱计算耗时

表3 面波勘探方法特征对比
高分辨率线性Radon变换法:抗噪性强,可解决缺失数据重建问题,有效进行多模式面波频散能量成像;但对信噪比较低的数据难以形成连续的频散能量,成像效果不佳。
频率分解法:抗噪性强,检波器分布不局限于等距直线排列,即对以任意几何形状参数排列的检波器采集到的Rayleigh波数据均能使用,适用范围广;但计算量大,处理数据较慢。
相移法:抗噪性强、计算量小、分辨率较高,对基阶模态的面波频散信息提取效果较好,降低Rayleigh波勘探方法对道间距的要求,使用较少道集即可直接产生分辨率较高的面波频散能量成像;但对高阶模态面波频散信息分辨率不高。
f-k变换法:计算量小,计算速度快;但要求采集时间间隔以及空间间隔相等,采集数据质量要求严格,容易发生空间假频问题,频散能量集中在一个很窄的频带范围,幅值最大原则下提取的频散曲线不稳定。
SFK变换法:抗噪性能强,可有效降低数据转换过程中频散能量的损失,频带能量分布均匀;但计算量大,耗时较长。
矢量波数变换法:抗噪性强,适用范围广,在成像分辨率和高阶模态成像质量上具有明显的优势,较少的地震道也能得到高质量的高阶模态成像;但计算量大,耗时较长。
3 结论
本文分析了τ-p变换法、高分辨率线性Radon变换法、频率分解法、相移法、f-k变换法、SFK变换法和矢量波数变换法等7种频散能量谱成像方法的技术原理和特点,得到以下认识:
1)7种计算方法均可有效地进行频散能量谱成像,在基阶频散曲线提取时效果差异较小,τ-p变换法、高分辨率线性Radon变换法、相移法和矢量波数变换法提取频散曲线精度较高,f-k变换法精度较低;在高阶模态频散曲线提取时效果差异较大,τ-p变换法、频率分解法、高分辨率线性Radon变换法和矢量波数变化法精度较高,相移法、f-k变换法精度较低。在多模态面波频散提取过程中,高分辨率线性Radon变换法和矢量波数变换法提取精度较高,f-k变换法提取精度最低。
2)τ-p变换法、高分辨率线性Radon变换法、相移法、f-k变换法高效简易、计算速度较快;频率分解法、矢量波数变换法、SFK变换法计算量较大,处理数据耗时较长。基于高分辨率线性Radon变换法、SFK变换法、相移法、频率分解法、矢量波数变换法的面波频散能量谱计算抗噪性较强,在实际面波数据处理中,可更好地拾取面波频散曲线。
