基于泊松方程的空间波数混合域二度体磁异常数值模拟

赵东东，王旭龙，周印明，戴世坤

1.中国地质调查局南京地质调查中心，南京 210016 2.中南大学地球科学与信息物理学院，长沙 410083 3.有色金属成矿预测与地质环境监测教育部重点实验室(中南大学)，长沙 410083 4.湖南科技大学信息与电气工程学院，湖南 湘潭 411201

0 引言

磁法勘探是地球物理勘探中发展比较成熟的方法之一，已经广泛应用于直接寻找磁铁矿及其共生矿床、固体矿产、石油天然气构造的普查和不同比例尺的地质填图以及深部、区域、全球构造的研究等[1-3]。在实际野外生产中，通常将走向方向尺度远比垂直走向方向尺度大的地质体近似用沿走向无限延伸的二度体代替。

目前，磁异常数值模拟方法一般主要分为空间域方法和频率域方法。空间域方法通过异常场解析式直接求取空间任意点的精确异常场，其优点是原理简单、结果精确，缺点是解析式比较复杂，推导过程繁琐，且当计算大量位置点异常场数据时，速度较慢。有关二度体的磁异常数值模拟研究最早就是在空间域开始的，Talwani等[4]首次给出了多边形截面二度体磁异常解析表达式；在此基础上，Talwani[5]在计算机上实现了近似二维棱柱状多边形数值模拟；Won等[6]根据泊松关系导出了多边形截面二度体磁异常的解析式，并利用Fortran77实现了相关算法，优势在于可以模拟地下任意观测点的磁场；Shuey等[7]、Rasmussen等[8]以及Cady[9]在前人研究基础上对原来的算法进行校正，使其能模拟实际地质体所产生的磁异常；贾真[10]系统地推导了均匀多边形截面二度体磁异常及磁异常梯度正演计算公式，并重点探讨了正演公式中所包含的奇异性；Jeshvaghani等[11]采用自适应有限单元法实现了基于拉普拉斯方程的二度体磁异常正演；Kravchinsky等[12]在Talwani[5]解析公式的基础上编写了一套基于Matlab的二度体磁异常模拟软件，并提高了数值精度。

频率域方法根据场源产生异常场的傅里叶变换解析表达式，通过数值方法计算该异常频谱的反傅里叶变换得到异常场。相对于空间域方法而言，其优点是表达式简洁，计算效率较高。在频率域，Bhattacharyya等[13]推导了任意二度体的磁场频率域表达式，并进行了反演研究；Pedersen[14]给出了任意二度体、二度半体(以三角形组合为其表面的模型)重磁异常频率域表达式，并指出该公式相对空间域解析公式更为简洁；吴宣志[15]将任意二维物体磁场的波谱解析表达式推广至可用于任意变磁化强度模型；柴玉璞[16]将偏移抽样方法发展为一整套完整的理论体系，有效提升了傅里叶变换的数值精度，使得频率域方法逐渐在处理复杂模型正演问题中得以广泛应用；吴乐园[17]在偏移抽样理论的基础上提出Gauss-FFT(fast Fourier transform)理论方法技术，有效提升了变换精度，降低了水平方向边界条件带来的影响，并将其应用于频率域二度体磁异常正演，取得了不错的效果。

然而，由于在面向实际应用的大规模、高效、高精度、精细化三维反演成像中，网格单元剖分数目达数千万甚至数亿，导致计算量和存储量巨大，使得常规从积分方程的空间域和频率域很难高效、精细模拟任意复杂模型；故在介于空间域和频率域之间的空间波数混合域，从微分方程角度出发提出一种可将三维或二维问题分解为多个一维小问题的数值求解方法。该方法已成功应用于二度体重力异常和三度体位场正演模拟[18-19]，并且在计算精度和效率方面表现出一定的优势。在此基础上，本文将基于泊松方程的空间波数混合域方法[18]用于磁异常二维数值模拟。该方法通过一维傅里叶变换把二维磁位问题转化为多个一维问题，由此大大减少了计算量，不同波数之间常微分方程相互独立，具有高度并行性；保留垂向为空间域，有利于适应复杂地形的模拟，兼顾了计算精度与计算效率；采用有限单元法求解不同波数满足的常微分方程，充分利用追赶法求解对角线性方程组的高效性以进一步提高计算效率[20]。在模型算例中，分别设计突变介质模型、连续介质模型和复杂地形模型用于验证空间波数混合域二度体磁异常正演数值模拟方法的计算精度与计算效率。

1 基本理论

1.1 控制方程

弱磁性体满足的二维泊松方程[21]为(详见附录A)

∇2U(x,z)=∇·M(x,z)。

(1)

式中：U(x,z)为磁位；M(x,z)为磁化强度矢量。对式(1)沿x方向做一维傅里叶变换，则有

(2)

1.2 边界条件

在无磁源区域，空间波数混合域磁位满足的常微分方程(式(2))通解为

(3)

式中，A和B为通解的系数，表示任意常数。规定垂向坐标轴向下为正，上边界z=zmin，下边界z=zmax，如图1所示。则上、下边界条件为：

(4)

1.3 磁场和磁梯度张量计算

空间域磁感应强度、磁梯度张量与磁位的关系如下：

图1 边界条件示意图

(5)

(6)

式中：B为空间域磁感应强度；T为空间域磁梯度张量。对式(5)和式(6)进行一维傅里叶变换可以得到：

(7)

(8)

1.4 零波数处理

特别地，当k=0时，空间波数混合域磁位满足的常微分方程为

(9)

式(9)相当于水平层状磁性介质产生的磁场，即空间波数混合域的水平磁场为零，垂直磁场为磁化强度的垂直分量，具体形式如下：

(10)

(11)

(12)

2 常微分方程求解

式(2)与引力位满足的空间波数混合域常微分方程类似[8]，本文采用基于二次插值的一维有限单元法进行数值模拟。该方法一方面能实现复杂模型和复杂地形的磁异常高精度模拟，另一方面利用追赶法求解有限单元法形成的对角线性方程组(五对角)具有计算速度快、占用内存小的特征。

联立式(2)和式(4)，即是空间波数混合域二度体磁位满足的一维边值问题。基于变分原理构造泛函[20]，可得到与边值问题等价的变分问题(详见附录B)：

(13)

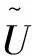
(14)

其中：

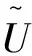
和列阵Xe、Ze详见附录C。由于δuT≠0，故

Ku=P。

(15)

对于该五对角定带宽线性方程组，采用追赶法实现高效、高精度求解，通过磁场、磁梯度张量与磁位之间的关系(式(7)和式(8))易得到空间波数混合域的磁场和磁梯度张量，采用Gauss-FFT对空间波数混合域磁位、磁场及磁梯度张量进行反变换，得到空间域的磁位、磁场和磁梯度张量[17-18]。

3 数值试验

设计截面为矩形的常磁化率和变磁化率二度体模型[21]，用于验证本文算法的正确性和可靠性。常磁化率和变磁化率模型空间展布及模型剖分参数均一致(图2)，模拟范围：x方向为-500～500 m，z方向为0～500 m，网格剖分规模为201×101，水平网格和垂向网格间距均为5 m；异常体x方向延伸范围为-100～100 m，z方向为150～300 m。本文算法均采用Fortran95语言编写，模型算例均在配置为CPU-i7-4790、主频为3.30 GHz、物理内存为32.00 GB的工作站上串行测试得到。

3.1 突变介质模型

图2a所示的突变介质模型中异常体的磁化率为0.01；给定地球正常磁场强度为45 000 nT，磁倾角为45°，磁偏角为0°。通过对比本文算法结果与解析结果[18]验证该算法的正确性和计算精度。图3为突变介质模型磁位、磁场、磁梯度张量数值解和解析解以及地面节点的相对误差。

从图3可以看出：突变介质模型磁位、磁场和磁梯度张量的数值解与解析解吻合较好，磁位最大相对误差绝对值仅为0.42%，磁场分量Bx和Bz最大相对误差均绝对值为0.48%；磁梯度张量的最大相对误差均绝对值为0.45%。磁位、磁场以及磁梯度张量的相对误差绝对值均小于0.50%，仅在零值线附近相对误差较大，验证了本文算法的正确性和可靠性，且精度较高。

a. 突变介质模型；b. 连续介质模型。κ.磁化率。

3.2 连续介质模型

设计磁化率随深度变化的连续介质模型(图2b)，用于进一步验证本文算法的适用性和可靠性。给定地球正常磁场强度为45 000 nT，磁倾角为90°，磁偏角为0°。异常体磁化率在深度方向上有二次变化规律：

κ=-(z-150)(z-300)×0.00001，
z∈[150,300]。

(16)

图4为磁化率连续变化的二度体模型数值解与解析解及相对误差。可以看出：连续介质模型磁位的数值解与解析解最大相对误差绝对值为0.004%，磁场Bx的数值解与解析解最大相对误差绝对值小于0.01%，与突变介质模型相比精度更高。这是由于连续介质模型在傅里叶变换过程中引入的误差较小。

左.解析解；中.数值解；右.相对误差。

a. U数值解与解析解；b. Bx数值解与解析解；c. U相对误差；d. Bx相对误差。

3.3 计算效率

在任意复杂模型剖分满足模拟精度的前提下，网格剖分规模越大，计算成本也越高；这是由于算法的计算效率主要由剖分网格规模决定的。图5给出了不同网格剖分规模的模拟时间，可以看出：当网格

图5 不同网格剖分规模的模拟时间

剖分为1 001×1 001时，模拟时间约为0.38 s，当网格剖分规模为2 501×2 501时，模拟时间为4.18 s；并且随着网格剖分的指数增长，计算时间仅呈线性增长，而不是指数增长。可见本文算法不仅计算效率较高，而且网格剖分规模越大，计算效率优势越明显。

3.4 起伏地形模型

设计水平地形模型(图6a)和起伏地形模型(图6b)，用于进一步验证本文算法在复杂起伏地形条件下的适用性和可靠性。模拟范围：x方向为-250～250 m，z方向为-100～200 m，网格剖分规模为501×301。在水平地形模型(图6a)中，异常体截面为矩形，沿x方向延伸范围为-100～100 m，沿z方向延伸范围为0～100 m；起伏地形模型(图6b)由山谷和山脊构成，异常范围与水平模型一致。异常体磁化率均为0.02，地球正常磁场强度为45 000 nT，磁倾角为45°，磁偏角为0°。利用本文算法计算观测线高度为地面以上100 m的磁场及磁梯度张量，计算时间为0.21 s。

地面以上100 m高度的磁场及磁梯度张量模拟结果见图7。可以看出：在山脊处，磁场Bz及磁梯度分量Tzz和Txz相对水平地形模型变化较快，正异常幅值增加，磁场Bx相对水平地形模型负异常幅值有所增加；在山谷处，磁场Bz和磁梯度分量Tzz和Txz相对水平地形模型变化减缓，但负异常幅值略有增强，磁场Bx相对水平地形模型变化明显减缓，进一步验证了本文算法在起伏地形条件下的适用性和可靠性。

图6 水平地形模型(a)和起伏地形模型(b)

a. 水平地形磁场；b. 水平地形磁梯度；c. 起伏地形磁场；d. 起伏地形磁梯度。

4 结论

1)基于泊松方程的空间波数混合域数值模拟，主要利用了沿水平方向傅里叶变换方法和追赶法求解定带宽线性方程组的独特优势，为二度体磁异常快速计算提供了一种新的研究思路和方案。

2)突变介质模型、连续介质模型和起伏地形模型的模拟结果表明本文算法数值模拟精度高、计算速度快，具有一定的实用价值。

3)该方法可能由于傅里叶变换的截断效应或强制周期性在介质突变边界引起较大的数值误差，有待在下一步工作中继续开展深入研究。

∇×H=0；

(A1)

∇·B=0。

(A2)

在高斯单位制(CGSM)中，B(Gs)和H(Gs)的关系为

B=H+M。

(A3)

式中：M是磁化强度，单位为emu，由感应磁化强度Ji和剩余磁化强度Jr组成。

M=Ji+Jr。

(A4)

且Ji与H成正比：

Ji=κH。

(A5)

式中，κ是磁化率。将式(A4)、式(A5)代入式(A3)可得

B=(1+κ)H+Jr=μH+Jr。

(A6)

式中，μ=1+κ是磁导率。将式(A6)代入式(A2)可得

∇·[(1+κ)H+Jr]=0。

(A7)

由于H由正常磁场强度Ho和异常磁场强度Ha组成，即可表示为H=Ho+Ha，令

Ha=-∇U。

(A8)

式中，U为磁位。将式(A8)代入式(A7)：

∇·[(1+κ)∇U]=∇·Jr+∇·[(1+κ)Ho]。

(A9)

又由于∇·Ho=0，且在只考虑弱磁性体的条件下，将式(A9)移项化简，有

∇2U=∇·(κHo+Jr)。

(A10)

式(A10)即为同时考虑感应磁化强度和剩余磁化强度的磁位基本方程。对于弱磁性体，式(A10)可以写为

∇2U=∇·M。

(A11)

在实际磁法勘探中，一般采用CGSM单位制,而CGSM单位制中磁场强度以奥斯特(Oe)为单位，其分数单位是伽马(γ)，1 γ=10-5Oe；在真空中μ=1，故B和H的量纲相同，它们的单位Gs与Oe大小相等，1 γ=10-5Oe=10-5Gs=10-9T=1 nT。

附录B

针对边值问题，构造一个泛函：

(B1)

其中：

(B2)

则其变分为

(B3)

将式(2)代入式(B3)可得

(B4)

将式(4)代入式(B4)得

(B5)

所以

(B6)

即空间波数混合域磁位的边值问题与下列变分问题等价：

(B7)

附录C

将整个区域的单元积分分解为各单元的积分之和，则

(C1)

令

(C2)

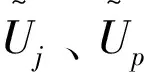
(C3)

式(C1)中第一项单元积分为

(C4)

其中，

(C5)

式中，l为单元长度。式(C1)中第二项单元积分为

(C6)

其中，

(C7)

式(C1)中第三项单元积分为

(C8)

利用形函数将jax、jaz表示为：

(C9)

其中：

(C10)

则式(C8)中第一个单元积分为

(C11)

其中，

(C12)

式(C8)中第2个单元积分为

(C13)

其中，

(C14)

式(C1)中，z=zmin、z=zmax分别为第一个和最后一个节点，可将其分别扩展成：

(C15)

其中，

(C16)

综上，可将式(C1)表示为

(C17)