顺层岩质边坡溃屈变形机制及失稳判定方法

2022-06-23吴朋宇张志红戴福初姚爱军

吉林大学学报（地球科学版） 2022年2期

吴朋宇，张志红，戴福初，姚爱军

城市与工程安全减灾教育部重点实验室(北京工业大学)，北京 100124

0 引言

层状岩质边坡在自然界分布广泛，根据岩层倾向和边坡坡向之间的关系，层状岩质边坡可以划分为反倾层状岩质边坡和顺倾层状岩质边坡两类。反倾层状岩质边坡一般较稳定[1-2]；顺倾层状岩质边坡由于其顺层构造特点，易发生沿软弱带的缓慢变形和层间剪切破坏，稳定性差，危害性极大[3-7]。溃屈型破坏是一种常见的顺层岩质边坡破坏模式，指的是在层状岩质边坡中，层面与坡面趋于平行，并由外界力、水压力和其自身重力所诱发的滑移-弯曲变形[8]，其形成条件和机制较复杂，具有隐蔽性[9-10]，已成为众多学者关注的焦点。

对于溃屈型边坡的研究早期多集中于对其成因机制的定性描述，这对于滑坡工程的勘查和防治指导意义不大，因此孙广忠[11]等学者开始采用力学手段和观点来解释说明层状岩体发生溃屈破坏的机制，之后许多学者也对此进行了研究[12-20]。在研究此问题的诸多方法中，能量法应用较广泛，其从能量角度出发，运算形式简洁统一，避免了直接利用力与变形的关系进行积分运算的复杂过程，受到广大学者重视。例如：李树森等[12]、刘均[13]基于弹性梁理论，利用能量法推导建立了失稳破坏的力学依据，给出了临界荷载和临界坡长的计算公式，刘均[13]还结合顺层边坡溃屈破坏的具体情况,提出考虑横向力作用下的边坡失稳计算理论和方法，但是以上研究在受力分析方面均偏于简单，在计算中主要考虑的是岩层自重对边坡溃屈破坏的影响；而黄洪波[14]、朱晗迓等[15]、肖慧等[16]、Qi等[17]、丁戈媛等[18]在受力分析方面考虑得更加全面，在自重基础上考虑了地震力、静水压力和锚杆等外力作用对边坡溃屈破坏的影响。上述分析皆建立于将边坡简化为梁来考虑，而在现实情况中，由于各种自然地质作用，在边坡上通常会有垂直于坡长方向的节理裂缝，边坡被分割成诸多不连续面，成为长度有限的岩石板，这种情况下若仍然将边坡视为梁来考虑，在研究的过程中会出现偏差，甚至会得出错误的结论。因此刘小丽等[19]根据弹性板的稳定理论，开始将顺层岩质边坡视为三维受压板，特别对边坡长度进行了考虑，利用能量法对边坡的溃屈破坏机制进行了讨论。冯君等[20]在刘小丽等[19]的基础上进行了改进，考虑了岩体材料的塑性变形影响，其认为应该根据岩层的实际应力状态将岩层视为弹塑性板来分析。但是二者均只考虑了岩层自重以及层间黏聚力和摩擦力的影响，而忽略了地震力、静水压力等外力作用对边坡溃屈破坏的影响。

综上所述，在对溃屈型边坡破坏机理的研究中，部分学者虽然对边坡的受力分析较全面，但运用的却是不考虑边坡宽度的弹性梁模型，这与实际情况不符；而另外一部分学者虽然运用了更加符合实际的弹/塑性板模型，但在具体分析时为了便于计算而忽略掉岩体所受的一些作用力，对边坡的受力分析偏于简单，研究成果具有一定的局限性。同时，已有研究成果对溃屈型边坡的结构失稳(溃屈变形)和滑动失稳(滑移破坏)两种失稳形式的判定方法不够清晰。本文在考虑岩层自身重力、地震力、静水压力共同作用的基础上，首先基于弹塑性受压板的稳定理论，利用能量法研究了顺层岩质边坡发生溃屈变形破坏的力学机制；然后在此基础上分别提出了溃屈型边坡结构失稳和滑动失稳两种失稳形式相应的稳定性判定方法，并针对不同状态的边坡提出了相应的防治措施建议；最后以四川省甘孜藏族自治州巴塘地区下归哇边坡为例进行了验证，以期为相关边坡防治工程提供参考。

1 模型建立

由于岩石材料的抗拉强度较小，边坡发生溃屈后岩层的挠度远小于其厚度，岩层整体变形不大。同时顺层岩质边坡的岩层厚度远小于岩层长度，岩层弯曲时产生的弯曲应力大于其中曲面应力，因此可按照小变形理论和弹塑性薄板理论进行分析。

图1为顺层岩质边坡的几何模型和弯曲变形模型示意图，其中，x方向表示岩层坡长方向，y方向表示岩层的走向方向，z方向表示岩层的法向方向。岩层沿x方向的长度为L，沿y方向的长度为b，沿z方向的厚度为h。其中L分为两部分：a为临界溃屈长度，即与底层脱离向外鼓出的弯曲部分AB段；L-a为驱动长度，即发生滑移的滑动部分BC段。其中A点代表岩层弯曲部分的下部边缘，B点代表岩层弯曲部分与滑动部分的交界处，C点代表边坡的后缘。岩层所受重力为G，所受地震惯性力为S，所受静水压力为Fw。岩层的倾角为α，重度为γ，滑动部分对弯曲部分的推力为P。

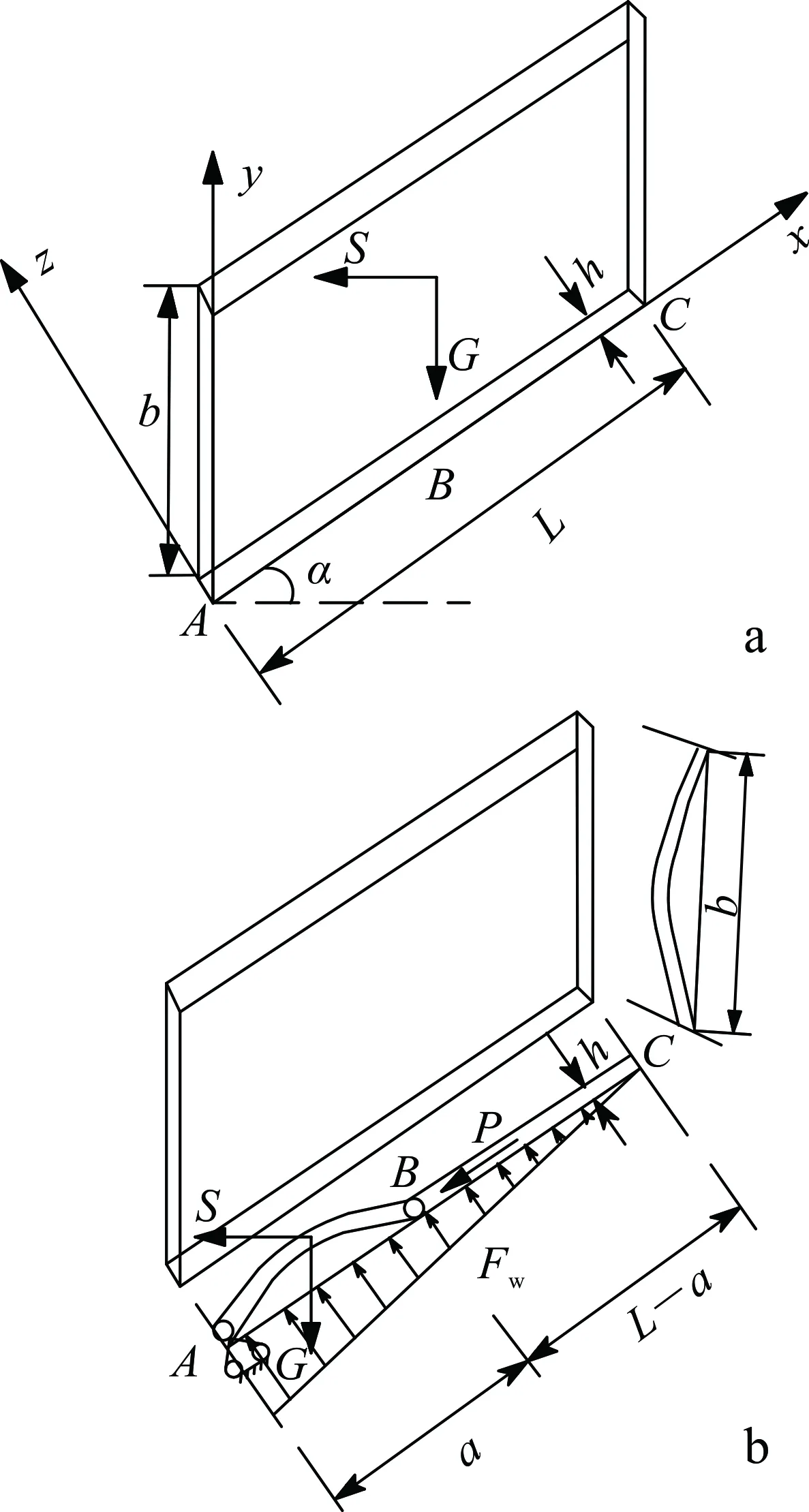
图1 边坡几何模型(a)和弯曲变形模型(b)

在对边坡岩层进行力学分析前作以下假设和简化：

1)当溃屈破坏发生时，岩层仅发生沿层面表层的滑动和弯曲，底部岩层不变形，视岩层为刚性板[13]；

2)地下水作用下的静水压力呈线性分布，作用力垂直于岩层表面，考虑最不利影响，即最高水位与地表平齐；

3)岩层的坡长方向即弯曲滑移方向；

4)图1b模型弯曲段的底边简化为铰支座约束，周边简化为辊轴支座约束[13]。

从图1b模型弯曲段的变形形状来分析，弯曲段的两端能够承受弯矩，把两端视为固定约束更合理。然而当发生溃屈破坏时，表层的弯曲段已经与底层分离，层间黏聚力丧失，滑动段也已经发生移动，层间只有很小的残余强度在起作用，而且岩体在受弯状态下极易产生破坏，抗弯能力迅速下降，无法承受较大弯矩，因此将弯曲部分的边界约束条件简化为底边铰支座、周边辊轴支座。

基于上述假设，将边坡的岩层简化为三维受压板，在自重及外力共同作用下发生溃屈变形。滑动部分对弯曲部分的推力P也是使下部岩层产生弯曲变形的主要动力，根据牛顿第三运动定律，P的大小等于弯曲部分对滑动部分沿x方向的合力P′；dN为单元体所受法向作用力；dFf为单元体所受摩擦力。为求P，沿坡长方向取厚度为h的滑动部分单元体，单元体的各边长方向分别对应x、y、z方向，作受力分析，见图2。

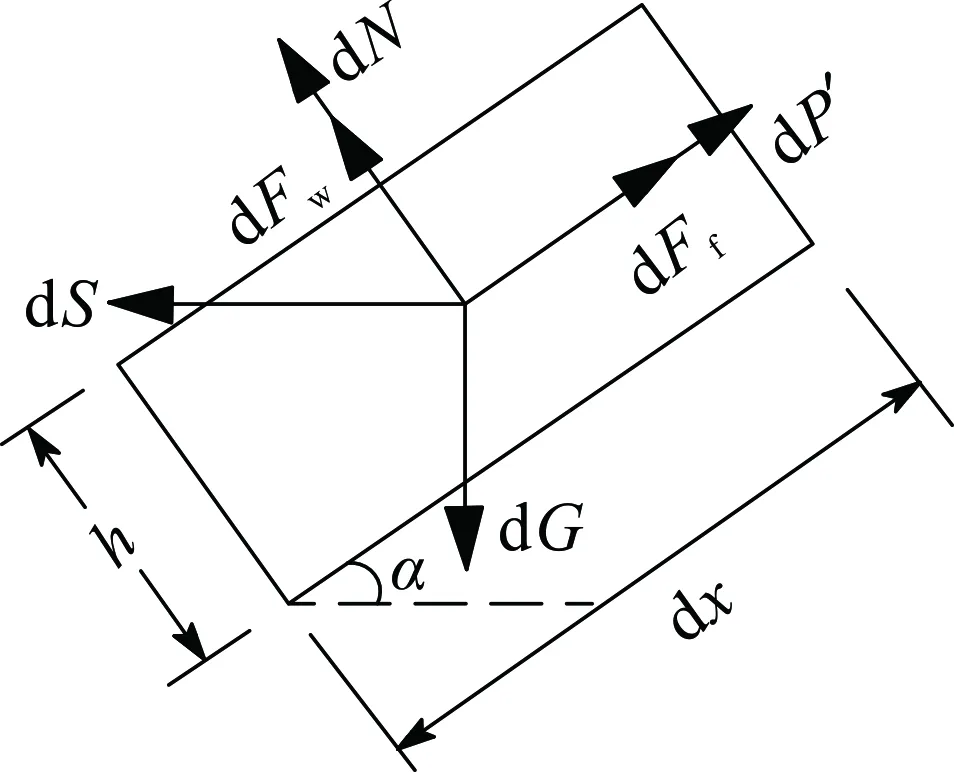
图2 单元体受力图

滑动部分单元体的自重力dG、静水压力dFw和地震惯性力dS分别为

dG=γhdxdy；

(1)

dFw=γw(L-x)sinαdxdy；

(2)

dS=βsKsγhdxdy。

(3)

式中：γw为水的重度；βs为动力放大系数；Ks为地震系数。滑动部分单元体所受法向作用力dN可以表示为

dN=dGcosα-dSsinα-dFw，

(4)

则单元体所受摩擦力dFf为

dFf=dNtanφ。

(5)

式中，φ为层间内摩擦角。

由于滑动面已发生移动，残余黏聚力较小，因此仅考虑层间摩擦作用。所以P′为

(6)

其中，

Q=γh(sinα-cosαtanφ)+
βsKsγh(cosα+sinαtanφ) 。

(7)

由P=P′得

(8)

本文将顺层岩质边坡的稳定问题简化为四边简支薄板的稳定屈曲模型，因此顺层岩质边坡的稳定性必然与边坡的x轴向和y轴向的长度都有关。在模型的约束条件下，其屈曲模态形式与曲面w=sinxsiny一致。同时根据薄板稳定性理论，在非受压方向(y轴)只有一个半波时,板的临界屈曲应力最小；同时在板屈曲过程中，仅考虑在受压方向(x轴)出现一个半波的情况，据此可将板的挠曲变形方程定义为

(9)

式中：w为板的挠度；f为板沿z方向的最大挠度。

方程(9)满足板的边界条件，即

w(x=0,x=a)=0；

w(y=0,y=b)=0；

z方向的最大挠度为

2 溃屈临界方程

采用能量法对边坡进行分析，自重及外力所做的总功ΔW等于岩体弯曲变形存储的变形能ΔU，即ΔW=ΔU，从而推导得到边坡发生溃屈变形的临界方程。

2.1 自重及外力做功

当顺层岩质边坡发生溃屈破坏时，岩层有弯曲变形的趋势，需分析岩层弯曲段的受力情况。在弯曲段模型中，不考虑岩层自重沿y方向的分力，同时根据薄板理论假设将岩层z方向的重力分量忽略[21]，因此仅考虑x方向的受力。则弯曲段的岩层受到P、G和S沿x方向分力的作用，由此可计算岩层所受的x方向中面合力Nx(方向为x轴负方向)，即

(10)

外力及自身重力所做的功可表示为

ΔW=Nx·dΔ。

(11)

其中，w′为w关于x的导函数。

因此，

将式(9)和式(10)代入式(12)，可得ΔW的表达式为

(13)

2.2变形势能

对于岩体材料这种复杂介质，当所受应力在弹性极限范围内时，其应力应变关系符合虎克定律，可视为弹性材料。但当应力较大以至超过岩体的弹性极限时，岩体将进入塑性变形阶段，此时，岩体的应力应变关系已不再是线性的，应看作弹塑性材料更为合理。

σ为材料所受应力；ε为材料的应变；σE为材料线弹性变形阶段所受极限应力。

图3 切线模量示意图

Fig.3 Diagram of tangent modulus

沿岩层的x方向，由于弯曲应力超过了弹性极限，材料模量变为了切线模量Et，所以x方向的弹性模量Ex=Et=ψtE；y方向的弹性模量不变，Ey=E。泊松比μ变化微小，所以μxy=μyx=μ。因此，考虑岩体材料刚度折减的变形能ΔU可以表示为

(14)

其中：

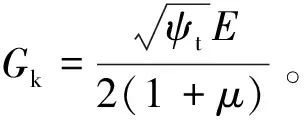
将式(9)代入式(14)中，得

(15)

2.3 能量法

假设岩层弯曲部分只受到P、G和S沿x方向分量的作用，所做的总功为ΔW，如式(13)所示。岩层无最初弯曲变形，且溃屈过程中不考虑岩体塑性发展，所以岩层由于弯曲变形而增加的变形能即为岩层全部变形能。将式(13)和式(15)代入公式ΔW=ΔU，可得

(16)

整理式(16)可得

(17)

下滑力定义为

(18)

临界应力定义为

(19)

当σ*>σcr时，边坡有失稳的趋势。

将R代入式(17),可得边坡沿x轴方向关于a的极限平衡方程：

(20)

3 稳定性分析

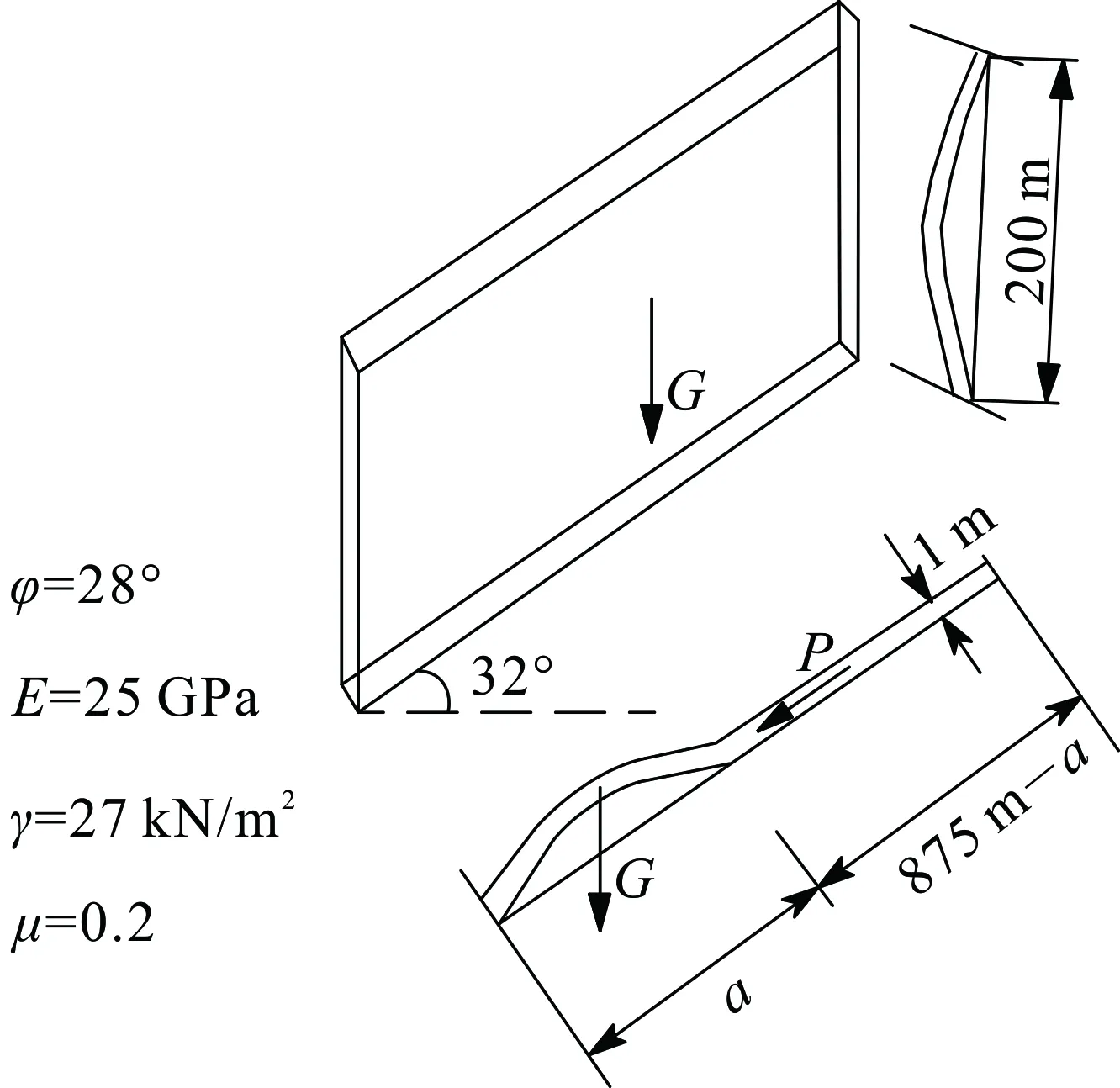
当边坡未发生溃屈变形时，将边坡的物理参量和几何参量代入式(20)中即可求出临界溃屈长度a的值。临界方程为关于a的四次方程，因此方程有4个根。但带入实际的边坡参数且经过大量计算，发现4个根中有2个虚数根和2个实数根，虚数根显然不符合实际情况，所以进一步选取2个实数根a1和a2(此处假设a1≥a2)。当满足0

当边坡发生初始溃屈变形之后，由于各种原因，溃屈长度可能会发生变化，导致边坡的稳定性也发生变化。将现场勘查所得实际溃屈长度a′代入下滑力计算公式(18)和临界应力计算公式(19)中对边坡的稳定性进行预判，对比a′与计算所得临界溃屈长度a1和a2之间的关系。当a2a1或者a′

4 算例分析

下归哇边坡是一个典型的溃屈型顺层岩质边坡，位于我国四川省甘孜藏族自治州巴塘县苏哇龙乡(图4)。岩层以斜长片岩为主，夹有云母片岩软弱夹层，软硬相间的岩体结构使得岩层容易发生滑动。层面平直粗糙、闭合，平均产状SW240°∠32°，边坡已产生明显的溃屈变形现象，如图5所示。根据奥维地图及现场勘查资料，取边坡坡长L=875 m，沿走向的坡长b=200 m，岩层厚度h=1 m，层面倾角α=32°。根据国内多项水利水电及边坡工程的实验数据，将黏聚力折算成综合内摩擦角，取φ=28°，岩层的弹性模量E=25 GPa，泊松比μ=0.2，重度γ=27 kN/m3。由于边坡表层岩层应力水平较低，仍处于弹性工作阶段，故取ψt=1。根据现场观察，下归哇边坡的变形破坏模式和边界条件可以使用文中所开展的溃屈分析变形模态形式和边界约束条件来进行分析，下归哇边坡的计算简图如图6所示。