基于电动车负荷和可再生能源协同优化的配电网调度策略

袁 欣，李 静

（浙江大学 工程师学院，浙江 杭州 310027）

0 引 言

随着环境污染和资源短缺的加剧，电动汽车以其无污染、充电便宜等优点受到推崇。 电动汽车因其灵活性和储能特性[1]，既可以作为用户侧的柔性负载，也可以作为电网[2]中的分布式供电设备。 通过合理的调度策略，电动汽车可以帮助电网缓解电力负荷和无序充电对电网造成的压力，实现减峰填谷[3-5]。 因此，电动汽车在配电网中的有效合理接入对于解决经济、环境和能源安全问题具有重要意义[6，7]。

同时，针对含电动车的配电网最优调度问题，国内外学者都已经进行了积极的探索。 文献[8]建立了电动汽车充放电正态分布模型，以在峰谷电价机制影响下使配电网运行成本和环境保护成本最小化为目标。 文献[9]中，在比较是否有电动汽车参与调度时，提出了电动汽车转换成本的概念，有效地证明了调度策略的有效性和正确性。文献[10]将电动汽车与可转移荷载相结合，设计了多种组合场景，分别建立了效率、经济性和安全性的多目标优化模型。 文献[11]提出了一种新的基于市场的微电网能源管理模型，该模型通过最优的能源销售、购买成本、收益之间的权衡，构建了微电网与能源和储备市场之间的可盈利的主动交换组合。 然而，上述文献中没有考虑配电网的潮流约束。 在对实际配电网进行优化时，应考虑电动汽车充电节点的地理位置限制和节点负荷增加引起的电压超限。 在文献[12，13]中，对于潮流问题，将混合整数非线性规划构造为易于求解的混合整数二次规划。 引入中间变量，将潮流方程转化为二阶圆锥形式，从而得到最优解。 在文献[14]中，提出了下垂控制策略下的孤岛电动汽车和负荷调度模型，并分别以经济优化和环境优化为目标，设计并演示了若干场景。

在上述研究的背景下，本文建立了包括光伏、风力发电机、电动汽车、可再生能源逆变器、储能和静态电容器组在内的日前多目标优化模型，以使配电网运行成本和用户充电成本最小化。 引入线性化原理[15]是为了解决潮流模型中的非凸、非线性[16]问题。 电动汽车有序充电策略可分为“固定功率”和“固定时间”两种模式。 结果表明，该策略显著降低了配电网的运营成本和用户的充电成本，成功验证了调度策略的可行性和有效性。

1 数学模型

1.1 配网数学模型

1.1.1 配网潮流模型

典型的n 节点径向配电网如图1 所示，其功率流关系可以用DistFlow方程来描述。

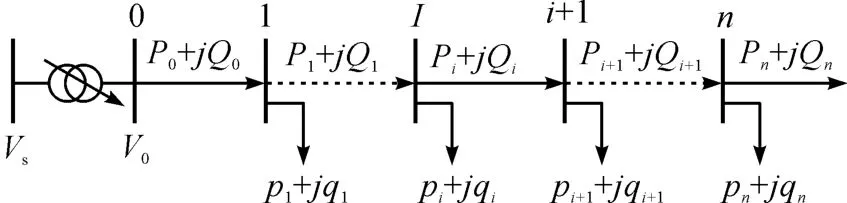
图1 典型的n 节点径向配电网

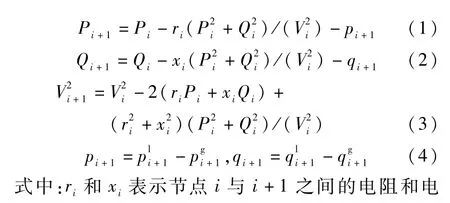
式中：Vs为线路的基准电压幅值。 简化后（4） -（6）的有效性和精确性已由相关文献[17，18]论证。

1.1.2 电动车充电需求模型

本文提出的电动汽车充电行为是通过工作场所停车场充电桩实现的。 当电动汽车进入停车场充电时，其状态可以用一维矩阵C表示：

C=[L，Ss，Se，Ts，Te，Ce，Pc] （7）

式中：L 为电动汽车的充电模式，包含有序充电和无序充电两种模式；Ss和Se分别表示电动汽车开始充电时的电荷状态和电动汽车离开工作时的期望电荷状态；Ts和Te分别表示电动汽车的上网充电时间和用户期望的离网时间；Ce和Pc分别表示电动汽车的额定容量和充电功率。

本文采用蒙特卡罗方法模拟用户充电需求，从而建立电动汽车负荷模型，这是一种随机模拟方法。 根据Ss和Se的采样结果，可以近似地建立电动汽车载荷模型。 根据文献[19]，车辆初始状态Ss的分布服从正态分布，期望可取0.6。 车辆最终状态Se的分布遵循近似的对数正态分布，期望可取0.9。

1.1.3 无功输出模型

在本文中，无功电源的输出主要来自节点的静态电容组（CB）和可再生能源逆变器。

1.1.4 储能模型

1.2 建立目标函数

1.2.1 配电网运行成本

式中：ω为权重系数（0≤ω≤1），它的值可以根据场景进行调整。

2 调度策略

为了实现配网的经济运行，需要考虑配网各电源的出力分布和负荷的调度，以及微配与主电网之间的电力交互。 在保证电网平稳、可靠运行的基础及电动汽车需求的前提下，将运维成本和用户成本在最低限度。

本文采用的调度策略如下：

（1）配网采用日前调度优化，其中每小时分为4 个时刻，全天分为96 个时刻。 记T1=00：15、T2=00：30、T96… =24：00；

（2）因为器件的响应时间不一致，将储能、分布式电源变流器的优化操作时间设为每15 分钟，无功电容组的操作时间设为每1 小时；

（3）优先利用风机WT、光伏PV等清洁能源，满足微电网负荷需求；当WT、PV的有功功率不能满足所有负载时，选择电池进行放电。 当系统有功充裕时，电池将充电储能；

（4）在配网选定的充电桩节点处存在电动车充电负荷，上班停驶来的电动车将在上午7 点至下午7 点完成充电任务。 当微电网的电量足够时，电动汽车可以自由充电。 当供电不足时，出于经济和稳定性考虑，电动汽车将转移充电时间或改变充电功率；

（5）电动车有序充电分为两种模式：第1 种是允许电动车在全过程中随时启停充电，为减少对系统的影响，该模式下电动车将采取最低充电功率充电；第2 种是要求电动车在规定的时间内完成充电目标，通过改变充电功率的大小来减少电动车负荷对配网的影响。 将这两种模式下的运行成本与配网无电动车、配网中电动车无序充电时的运行成本作对比，体现调度策略的优势。

通过对3种吸附黄酮效果良好的树脂进行静态吸附及解吸试验，确定了吸附分离红薯叶黄酮的最优树脂为AB-8大孔吸附树脂，与任云霞等[10]、洪雪娥等[11]研究结果一致。通过正交试验得到其最佳吸附条件为：上样液浓度300 mg/L、流速2 mL/min、上样液pH 5.0，其对红薯叶总黄酮吸附率可达66.8%；最佳解吸条件为：洗脱液浓度90%、洗脱液流速4 mL/min、洗脱液用量5 BV，树脂的解吸率可达70.3%。

具体流程见图2。

图2 含电动车负荷的配网协同优化策略

3 算例分析

3.1 算例数据

如图3 所示，选择典型的IEEE33 节点拓扑配网系统进行分析。

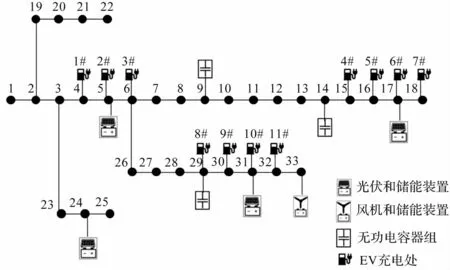
图3 节点配电网示意图

本文算例系统中设立11 个充电桩；电容器组安装在10、15、30 节点处，光伏发电装置安装在5、17、24、31 节点，风电安装在33 节点处，储能装置安装在5、17、24、31、33 节点，具体配置参数如表1 所示。

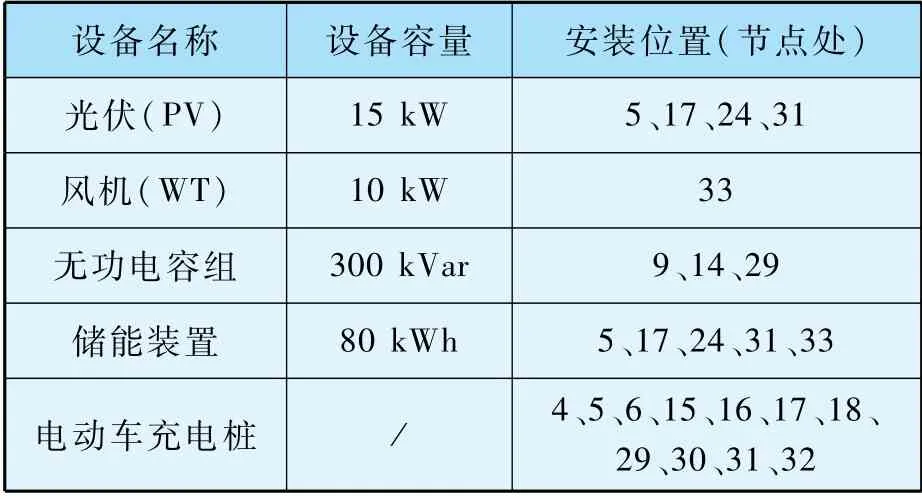
表1 系统节点设备配置表

光伏数据采用浙江省某地光电场2018 年某日的观测数据，风电数据采用文献[21]中对某风电场蒙特卡罗模拟后预测数值。 为了使仿真效果更为明显，对系统原负荷数值作了细微调整。 其中，针对系统潮流约束，设主网节点1 的电压为1.0 pu，电压的幅值范围为-7% ～+5%。

电价如表2 所示[22]，分为谷时段电价（00：00—7：00）、平时段电（8：00—10：00，16：00—18：00，22：00—24：00）和峰时段电价（11：00—15：00，19：00—21：00）。

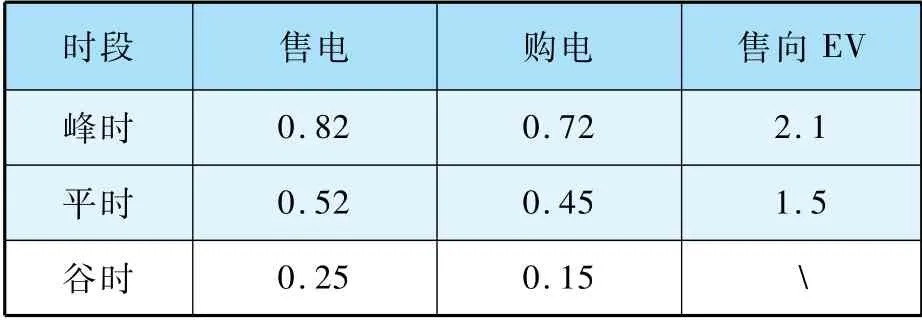
表2 分时电价表 单位：元/kWh

配网的日电力负荷曲线、可再生能源发电PV和WT有功功率曲线如图3 所示，其中日负荷标定值为300 kW，光伏和风机出力的标定值分别为15 kW、10 k W。

为验证电动车负荷优化调度对配网综合成本的影响，设计四种场景，将电动车充电功率考虑为恒定和变动两种情况纳入对比：

场景一：电动汽车充电负荷不接入配网系统，综合考虑可再生能源、储能、无功电容组协作优化，获得最优调度结果；

场景二：电动汽车负荷接入配网系统后，实行无序充电，调度可再生能源和储能、无功电容组，得到最优结果；

场景三：电动汽车负荷接入配网系统后，在每个时刻内保持固定最低充电功率，通过调节充电的具体时间来实现配网运行成本和用户充电最低；

场景四：电动汽车负荷接入配网系统后，在规定时间内完成充电任务，通过调节充电的功率，来实现配网运行成本和用户充电成本最低。

3.2 算例结果与分析

3.2.1 无电动车负荷的配网协调优化

从图4 中可以看出，配网系统中负荷高峰时间主要出现在每天的12 点至15 点之间，同时在线路的4# -8#、15# -20#、29# -33#节点处，配网自身负荷处于相对低谷的状态，所以可以考虑在对应节点附近设立充电桩，以满足电动车充电需求。

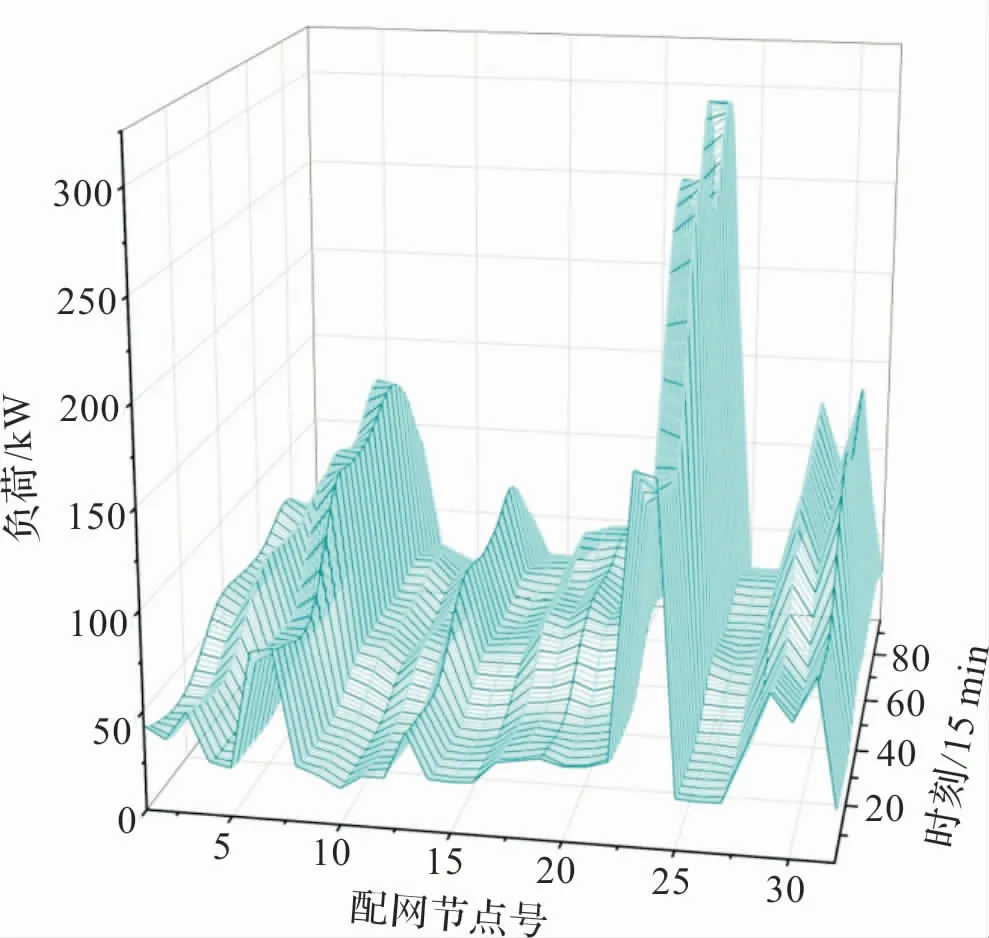
图4 系统各节点负荷曲线图

此时，为缓解配网负荷压力，光伏和风机、无功电容组、储能装置将有机结合起来。 其中，分布式电源变流器的无功出力将与无功电容组配合，缓解支路的压降压力。 储能装置在配网有功功率富余时，将充电以储备电量；在配网有功稀缺时，将放电来满足配网的有功平衡。

在图5 中，无功电容组整体出力的曲线趋势与配网负荷波动一致，存在10 点-15 点，18 -21点两个高峰时刻。 其中线路末端的29#电容器组为平抑更多的压降，所以其出力处于同期节点中的较高水平。

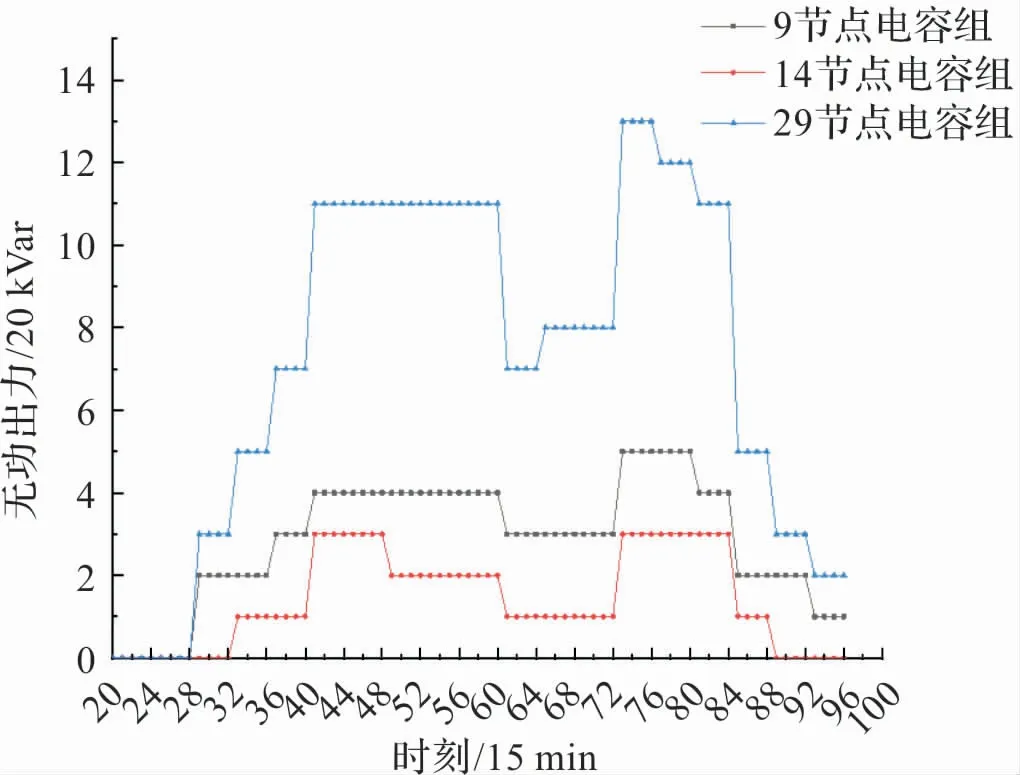
图5 无功电容组出力图

3.2.2 电动车无序充电下的配网协调优化

电动车负荷接入配电网后会一定会给系统带来更大的压力。 从下面的各变流器出力的前后变化可以看出EV接入后的差异。

从图6 中可以看出，分布式电源的有功输出从8 点之后逐渐爬升，在15 点后逐渐下降。 而相应节点处的变流器的无功功率大致从7 点开始出力，随着线路负荷的增加，一直到18 点之后出现下降。 特别是24#、31#节点，由于处于线路末端，为平抑线路压降带来的其无功出力处于同期节点中的较高水平。

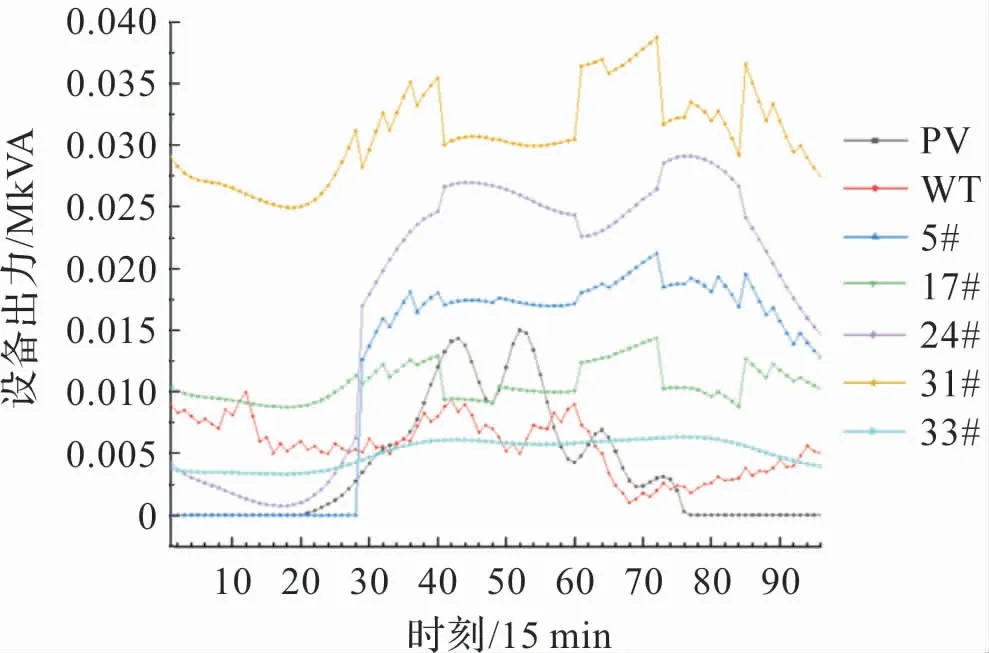
图6 无EV时各电源及变流器出力曲线

在图7 中，当电动汽车负荷加入配网后，系统中的负荷增加，体现在分布式电源的无功出力显著增加。 与图6 中曲线的数据对比可知，5#节点处变流器的无功峰值从0.023 升到0.032。 31#节点的无功峰值从0.037 升到了0.051。

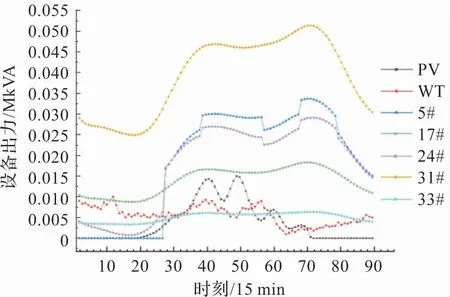
图7 含EV时各电源及变流器出力曲线

从图8、图9 的储能装置的曲线也可以得到，当配网系统中增加额外的电动车负荷时，储能的SOC状态整体是低于初始值。 在同样的21 点时刻，无电动车时的SOC已经超过0.6，达到了0.63，而增加了电动车负荷后的储能SOC还不到0.54。 这意味着，一旦系统中用户负荷或者电动车充电量增大，储能的容量可能就不能满足配网调度需求。

图8 无EV时储能SOC曲线图

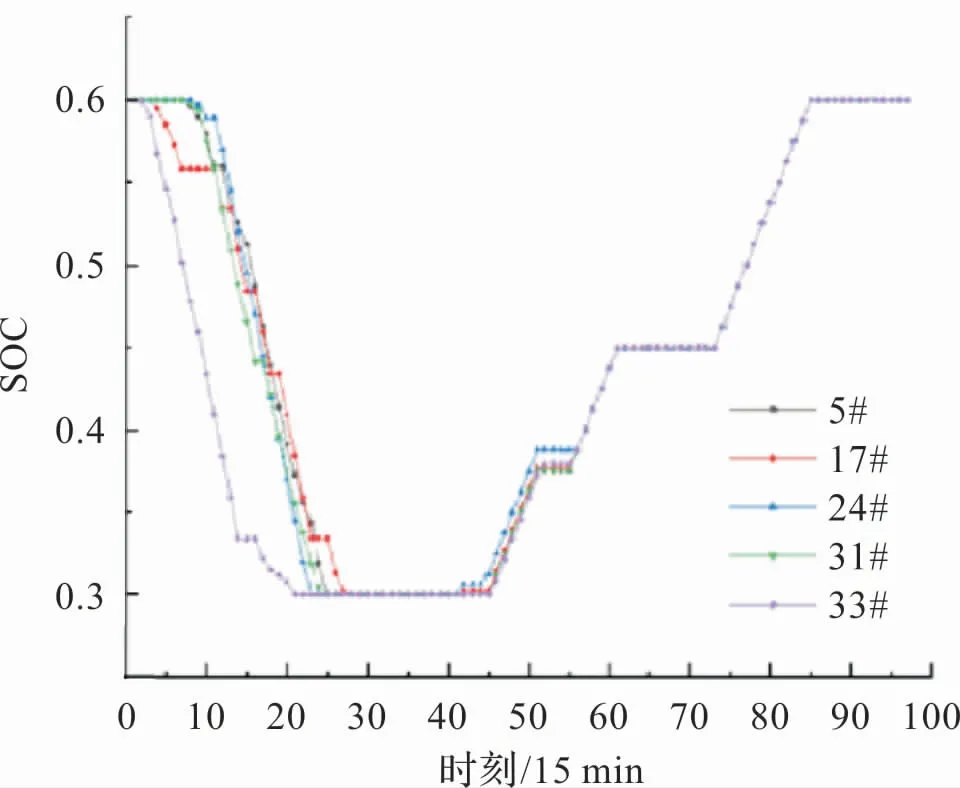
图9 含EV时储能SOC曲线图

综合对比可得：电动车负荷的加入从各个方面都会给系统整体协同优化带来负面影响，此时需要更好的有序充电策略来改善这一情况。

3.2.3 电动车两种有序充电模式的分析研究

当电动车负荷接入配网中，通常认为其总的充电需求时不可调节。 即Ss、Se不作调整，故调度优化电动车一维状态矩阵C中的Ts、Te和Pc变量。

当电动车以较低固定功率（2 kW）充电时，充电桩会根据系配网运行的情况，选择恰当时间并入配网负荷。

如图10 所示，图中零散的柱线代表该节点电动车当天的充电状态。 11 个充电桩处的电动车在给定的时间段内完成各自的充电需求，充电时间较为灵活。 但这样的充电方式要求电动车长时间停留在充电桩处，同时会引起电动车电瓶的频繁关断，对车辆造成额外的损伤。 故提出另一种充电策略，即确定电动车具体的充电窗口时间，灵活地改变电动车瞬时充电功率，以减少对配电网的冲击。

图10 定功率电动车充电功率示意图

当电动车确定充电时间，如图11 所示，各电动车在选定的2 个小时内完成各自的充电需求。在每个时刻内，充电功率从1 ～3 k W 灵活变化。在完成车辆的充电需求后，电动车才与配网断开联络。 在该模式下，电动车的开断次数和停泊时间都大大减少。

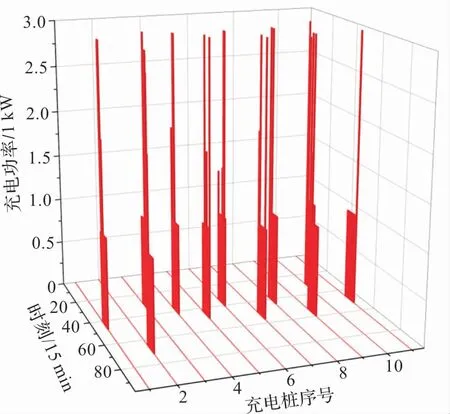
图11 定时长电动车充电功率示意图

表3 将4 种充电模式的成本进行详细对比。

表3 成本分析表 单位：元

由表中可知，电动车以无序充电的方式接入，大大增加配网购电及整体运维的费用。 但通过有序充电等方式，可以大大降低网损的影响。 同时，在EV接入的三个模式中，定功率的综合运维成本最低，比无序充电少了45.26 元，比定时长模式少了5.38 元。 因为，无论是对配网侧还是对用户侧，定功率模式下的电动车负荷调度更加灵活，负荷更加分散，避免了扎堆带来的成本增加。 但是，定时长模式的优势在于确定了电动车的充电时间范围，且更少的充电次数更适应用户和车辆的良好使用习惯。

值得补充说明的是，本文所研究的配网及充电车规模较小。 当系统中电动车的规模大大增加时，本文所提的充电优化及可再生能源优化的成果将更为显著地增加。

4 结 论

本文建立了一个包括光伏、风机、分布式电源变流器、无功电容组、储能装置、电动汽车的配电网仿真模型。 通过简化将非凸、非线性的潮流约束转为方便求解的线性规划问题。 针对电动车的充电需求，提出了两种灵活的电动车有序充电策略。 利用蒙特卡洛方法模拟电动汽车有序和无序充电行为，仿真结果表明，本文提出的有序充电策略能够有效实现“避峰填谷”和用户经济性充电的双重目标，尤其在电动汽车规模化应用后效果将更加明显。

从长远看来，EV用户的使用习惯和车辆状态会比本文中的假设要复杂得多，如何准确地建立用户的行为模型还需要更多的研究。 如果对电动车的入场、离场时间等不确定的随机量建立更多的场景预测，将给结果带来更强的实用性。