多线程快速排序算法的设计与优化

李添锐,曹庆年,孟开元

(西安石油大学 计算机学院,陕西 西安 710065)

0 引言

排序问题不仅是计算机科学中非常重要且应用广泛的问题之一,而且在计算机图形学、系统决策、搜索引擎等领域有着重要地位,并曾在2000 年被评为对工程和科学计算研究与实践影响最大的十大问题之一[1-4]。有资料显示,系统在处理排序问题上,中央处理器(Central Processing Unit,CPU)的时间占比很大,可达20%～60%[5]。在传统的内部排序算法中,由Hoare 提出的快速排序(Quick Sort)是一种效率相对较高的算法,但待排序列长度较长(大于106)时,其时间成本依旧较高。因此十分有必要对快速排序算法进行进一步优化。

线程(Thread)是操作系统能够进行运算的最小单位。一个处理排序的进程,若采用快速排序算法,其划分的两个子序列可分别由两个并行执行的线程完成。在划分的子序列长度相同的情况下,时间消耗仅为串行执行的50%。将多线程技术引入快速排序算法,可以大大提高排序效率。

1 快速排序以及传统优化方法

快速排序的主要步骤可以简化如下:

虽然快速排序的效率是内部排序算法中最快的,但在算法第4 行中,若划分的“标杆”选取不当,在极端情况下,每次划分的两个子序列长度都分别为0 和原长度减1,此时不仅时间复杂度高至O(n2),且极易引起栈溢出(Stack Overflow)导致排序失败。同时对于大量重复元素的待排序列,无论怎样选取“标杆”,均无法避免上述问题。为了克服快速排序的缺点,传统的优化方法如下。

1.1 标杆选取

可以先将序列中的随机某个元素与首元素交换,再将首元素作为标杆。此种方法被称为“随机标杆”法,但会因为生成随机数而增加额外的开销。“三数取中”法可以避免此问题,其基本思想是先将序列的中间元素、首元素和末元素进行升序排序,再将首元素作为标杆。但以上两种方法都无法解决大量重复元素序列的问题。

1.2 三轴排序

在每次序列划分之后,从“标杆”出发,将两个子序列中和“标杆”相等的元素均交换到“标杆”的左右两边,最终将原序列划分成3 部分。通过采取适当的交换方法,排序整体的复杂度不会改变,同时减少了左右子序列的长度。此种算法极大地改进了大量重复元素的序列。

1.3 引入插排

当待排序列较短时,采用分治递归操作所需的开销已经大于简单排序的开销,故引入插入排序处理较短的子序列。此方法的难点在于最小分段阈值k的选取,k为经验值,由系统的递归开销等因素决定。在Java 中,此k值取为32 效果最佳[6]。在C++的内置sort()函数中,k值为16,一般情况下5～25 均可。

2 多线程优化方法

多核CPU 的出现使得多线程编程方法成为可能,同时也为许多传统经典算法进一步优化提供了新思路[7]。

2.1 子线程处理子序列

快速排序中的递归操作中,可以创建子线程处理其中1 个子序列。在多核CPU 系统中,线程会分配到不同的核心上并行执行,于是处理子序列的时间可大大缩短。引入多线程编程处理后的算法如下:

由于线程创建需要时间,在递归操作时可选用较短子序列交由子线程处理。

2.2 根据最大线程数的改进

上述算法适用于无限创建线程的理想化模型,而实际情况中线程数受限于CPU 核心数,故须改进。引入多线程编程的深度d这一额外参数,d=0 时为传统串行方法;d>0 时,构建新线程执行子序列,同时d自减1。d的值由系统CPU 核心数N决定,通常d取■log2N」。

2.3 采用线程池

当待排序列为随机序列时,一次快排划分后的两个子序列的长度不同。因此会出现先前创建的线程已经运行结束而释放,后续的待排子序列无法创建新线程的现象。为此可以创建线程池,当线程池饱和时,采用传统串行算法,这样可以时刻充分利用CPU 的各个核心。

2.4 性能测试

性能测试采用传统串行快速排序和多线程优化快速排序两种方式分别对8 000 000 个随机数据进行排序,并对其时间消耗进行对比,从而得出多线程优化方法的改进幅度。

在Intel(R)Core(TM)i7-6700 CPU@3.40 GHz 4核8 线程CPU 的PC 上使用C++多线程编程实现2.1中的算法并进行测试。通过多次测试取平均值,测试结果如表1 所示。

表1 优化结果比较

由于测试主机为4 核主机,故算法执行中最多有4个CPU 核心同时工作。从测试结果可以看出,4 核心多线程优化快速排序算法的所需时间仅为传统串行快速排序算法的1/4。

3 优化上限分析

显然,当待排序列为升序序列,即经过“三数取中”法后为最好情况时,采用多线程编程的优化幅度达到最大。

3.1 时间复杂度分析

在最好的情况下,设长度为n的序列的划分操作时间消耗为P(n),不难得出:

其中,c为执行1 条指令所需时间,设单位为us。

不妨设n=2^(k+1)-1,k=0,1,2,…如此可保证每次划分都是最优划分。

传统串行快速排序的时间消耗为:

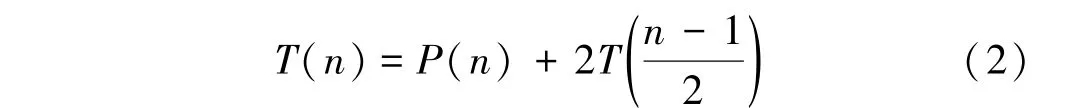
推导后得:

若当前CPU 的核心为2,多线程深度d=1,设系统创建1 个子线程的所需时间为td,此时多线程优化快速排序的时间消耗F1(n)为:

推导后得:

相对于传统单线程快速排序,时间节省率H1(n)为:

类似地,可以由数学归纳法得到d=k时的时间消耗Fk(n)和时间节省率Hk(n)

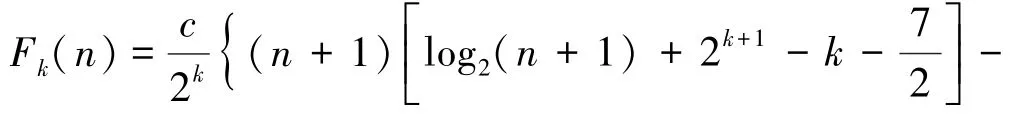
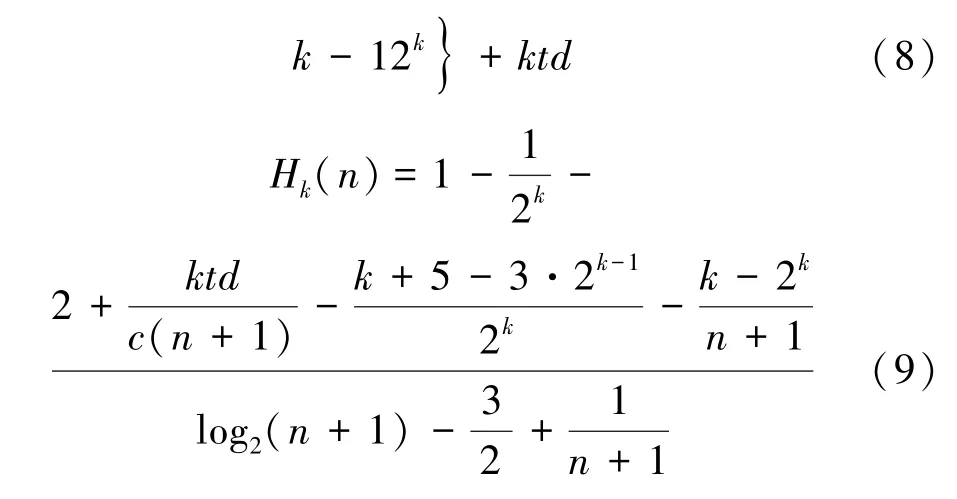
通过公式(9)可以看出,时间节省率Hk(n)是线程深度d和待排序列长度n的函数。

在保证n≫d的情况下,n和d越大,节省率越高。

3.2 理论验证

为验证3.1 中的公式正确性,采用2.2 中的算法C++来实现,待排序列长度n取1 048 591,线程深度d分别取1,2,3,经过测试,平均td=150 μs,c=1.5×10-3μs,待排序列取最优序列。验证结果如表2 所示。

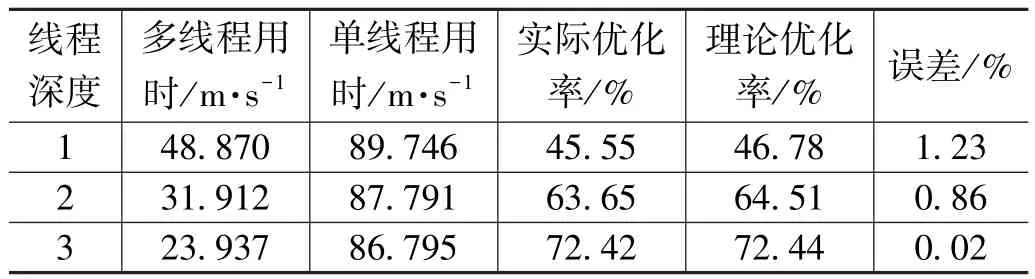
表2 理论验证结果

可以看出,实际运行结果和理论分析极为接近,因此,3.1 的理论分析得到了验证。

4 结语

快速排序是所有内部排序算法中平均性能最优的算法,但其本身具有许多不足之处。本文在C++平台中实现了对快速排序递归操作的进一步优化,通过建立子线程并发处理两个子序列,使得排序速度得到了大幅提高。

通过对多线程快速排序的理论分析,本文提出了此方法在优化程度上的理论上限。在实际应用中,由于每次划分的子序列长度不一,因此保证线程的利用率便成了多线程算法中的关键。

由于内存和CPU 核心数量的限制,不宜做更大数据量和更多线程的测试。将来的实验中可以考虑其他环境,进一步验证优化理论,分析线程调度的开销等其他因素,以确定更精确的参数,进一步优化排序性能。

和CPU 相比,GPU 的并行计算能力更加强大,使用CPU 优化也是对快速排序的一种优化方式,在未来的实验中也可尝试使用GPU 优化并和CPU 算法做对比[8]。