基于密度峰值聚类算法的自适应加权过采样算法

穆伟蒙，宋 燕，窦 军

（1 上海理工大学 理学院，上海 200093；2 上海理工大学 光电信息与计算机工程学院，上海 200093）

0 引言

数据不平衡问题在许多应用，如医疗诊断、人脸识别和网络诈骗等领域都受到了广泛关注。不平衡问题是指不同类别的样本数量差距很大，样本数量多的类别称为多数类，样本数量少的类别称为少数类。一般来说，少数类样本包含很多有用的信息，如果没有很好的分类，可能会付出很大的代价。因此，提高少数类的识别精度至关重要。

解决不平衡问题的方法可以分为2 类：基于数据的和基于算法的。其中，算法层面的策略包括代价敏感学习、单类学习、集成学习等，主要通过修改现有算法来提高对少数类样本的分类精度。数据层面的策略包括过采样技术和欠采样技术，通过调节多数类或者少数类的样本数量使不同类别的样本趋于平衡。总地说来，欠采样技术能够减少多数类样本来使类趋于平衡，容易实现，但易造成有用信息的丢失。而过采样技术既能使不同类别样本达到平衡，又能保留原始数据的分布特点，所以过采样在处理不平衡数据分类方面得到了更多的关注。

由于过采样技术应用更为广泛，因此有学者提出了许多过采样方法，如，为了解决随机过采样技术可能会造成的过拟合问题，Chawla 等人提出了合成少数类过采样技术（Synthetic minority oversampling technique，SMOTE），其原理为：对于任意一个目标少数类样本x，利用欧式距离随机选取x的其中一个近邻样本x，通过线性插值，人工合成样本x，即：

其中，∈ [0，1] 。

虽然SMOTE 在一定程度上克服了过拟合问题，并解决了类间不平衡，但是SMOTE 合成样本时，对于所有的少数类样本，采用统一的样本分配策略合成新的样本，很容易造成类内不平衡，改变原始数据的分布。

为了解决上述问题，学者提出了加权过采样方法，为不同的子簇或者样本分配不同的权重，来解决类间不平衡和类内不平衡问题。He 等人提出了自适应合成过采样（ADASYN）方法，来对每个少数类样本赋予不同的权值，而权值越大，学习难度就越大。Nekooeimehr 等人提出自适应半无监督加权过采样方法（A-SUWO），通过利用分类复杂度和交叉验证来自适应地确定每个子簇的过采样大小。Douzas 等人提出基于K 近邻（KNN）过采样算法（SMOM）来给每个目标样本的近邻分配选择权重，对可能会产生过度泛化的方向赋予较小的选择权重。此外，为了增强边界少数类样本的学习，安全水平过采样（Safe-Level-SMOTE）算法、边界过采样（Borderline-SMOTE）算法和多数加权少数的过采样（MWMOTE）即已陆续提出。虽然如上研究通过不同的方法对少数类样本赋予一定的权重，但却没有充分考虑少数类样本权重分配所必须的因素，如样本间的相似性、样本分布特点等，这也是本文的主要研究背景。

针对上述问题，本文提出了一种基于密度峰值聚类算法的自适应加权过采样算法（DPCOTE）来解决不平衡分类问题。该方法核心思想为：

（1）利用k 近邻算法去除多数类和少数类噪声样本。

（2）基于密度峰值聚类算法中的重要因子，为每个少数类样本赋予采样权重，以此来为少数类样本合成不同数量的新样本。

（3）在DPC 算法中，引入马氏距离，来消除样本特征间量纲不一致的问题。

1 基于密度峰值加权过采样方法

1.1 马氏距离

马氏距离是由印度统计学家Mahalanobis 提出的，马氏距离考虑了各个特征变量之间的联系，且不受特征量纲不一致的干扰。马氏距离与欧氏距离的关系示意如图1 所示。由图1 可知，在计算欧式距离时，与距离最近，但是在马氏距离中，与距离最近，因为原始数据呈现椭圆分布，欧氏距离没有考虑数据分布。马氏距离除以协方差矩阵，可以把各个分量之间的方差都除掉，消除了量纲性，详见图1（b）。

图1 马氏距离与欧氏距离示意图Fig.1 The schematic diagram of Mahalanobis distance and Euclidean distance

如果协方差矩阵是单位矩阵，则马氏距离等同于欧氏距离。

1.2 密度峰值聚类算法

密度峰值聚类算法（Density peaks clustering algorithm，DPC）由Rodriguez 等人于2014 年提出。该算法无须迭代就可确定聚类中心，且能够识别任意形状的类簇，目前已经得到了广泛的应用。DPC 算法的核心思想建立在2 个基本假设上：

（1）聚类中心被局部密度较低的邻域点包围。

（2）密度较高的点之间的距离相对较大。

基于这2 个假设，DPC 引入了2 个重要因子，即目标样本的局部密度ρ和相对距离δ。对于第一个假设，利用高斯核函数计算任一样本点x的局部密度ρ，其值可由如下公式计算得出：

其中，d为样本x和x之间的距离，d为截断距离，通常将其设为距离降序排列的1%～2%。

DPC 算法示意如图2 所示。在确定了截断距离后，就可以得到目标样本的局部密度，如样本点，，。对于第二个假设，通过计算相对距离，即对于任一样本点x，其局部密度比其更大、且距离最近的样本点x的距离δ可表示为：

图2 DPC 算法示意图Fig.2 The schematic diagram of DPC

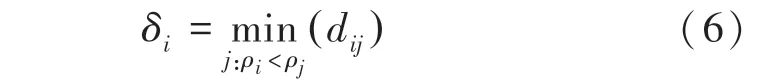
在计算出所有样本的因子后，如果样本的ρ和δ足够大，其附近样本分布较为密集，则将其视为密度峰值。

1.3 DPCOTE 方法

在本节，提出了新的基于密度峰值聚类算法的过采样算法（DPCOTE）。该算法中，使用马氏距离代替DPC 算法涉及到的欧氏距离。该算法主要步骤可阐释分述如下：

（1）去噪。在数据预处理阶段，使用k 近邻算法去除噪声样本。在此阶段中，对所有的样本使用k 近邻算法。先是计算目标样本与近邻样本的距离，找到目标样本的个近邻。如果目标样本的个近邻样本的类标签与目标样本的类标签都不一样，则将目标样本归为噪声样本，并删除。

（2）合成样本。利用DPC 算法对所有少数类样本赋予采样权重，来确定每个少数类样本需要合成的样本数，并使用k 近邻算法和线性插值来对每个少数类样本合成新样本。

和传统的DPC 算法不同的是，本文在计算任意2 个样本的距离时，使用马氏距离代替欧氏距离，这样就解决了特征间量纲不一问题。所以，利用上述描述的DPC 算法，基于马氏距离，可以得到每个少数类样本的局部密度ρ和到局部密度较高的最近邻的距离δ（1，2，…，），此处的表示少数类样本数。

下面，利用ρ和δ来确定每个少数类样本的采样权重。为此，先对这2 个因子做归一化，即：

综合上述2 个因子，考虑到每个少数类样本的密度信息和相对距离信息，为此构造一个新的因子，即：

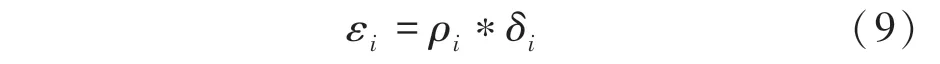
事实上，如果样本的密度较大，基于该样本合成新样本时，会生成较多重复的样本，导致模型过拟合。所以，每个少数类样本需要合成的样本数与密度成反比，具体数学公式如下：

将其标准化来确定第个少数类样本的采样权重为：

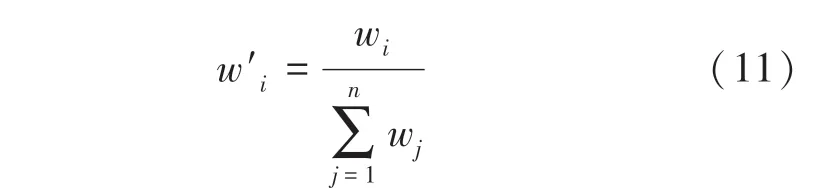
若给定为需要合成的少数类样本总数，则第个少数类样本需要合成的样本数可以通过下式得到：

确定每个少数类样本的合成数后，利用k 近邻算法和线性插值来合成新的样本，使少数类样本与多数类样本达到相对平衡。图3 为ADASYN 算法和本文提出DPCOTE 算法生成的样本分布示意图。图3 中，表示多数类样本，表示少数类样本，表示新合成的少数类样本。由于ADASYN 算法对于学习难度高的样本赋予更高的权重，所以其在边界附近合成了更多的样本，容易模糊类边界，DPCOTE 算法考虑每个少数类样本的分布情况，在不改变原始数据分布的情况下，生成更多有用的新样本。图4 给出了DPCOTE 算法的流程图，相应算法的伪代码设计表述具体如下。

图3 合成样本分布示意图Fig.3 The schematic diagram of synthetic sample distribution

图4 DPCOTE 算法流程图Fig.4 Flow chart of DPCOTE

2 实验结果及分析

2.1 数据集

为了更加全面地验证DPCOTE 算法的性能，本文从UCI 机器学习库中选取了12 组二类不平衡数据集，这些数据集样本数量和特征数量都不同，且不平衡率的范围为2.78～22.7。表1 为本文选用的数据集。

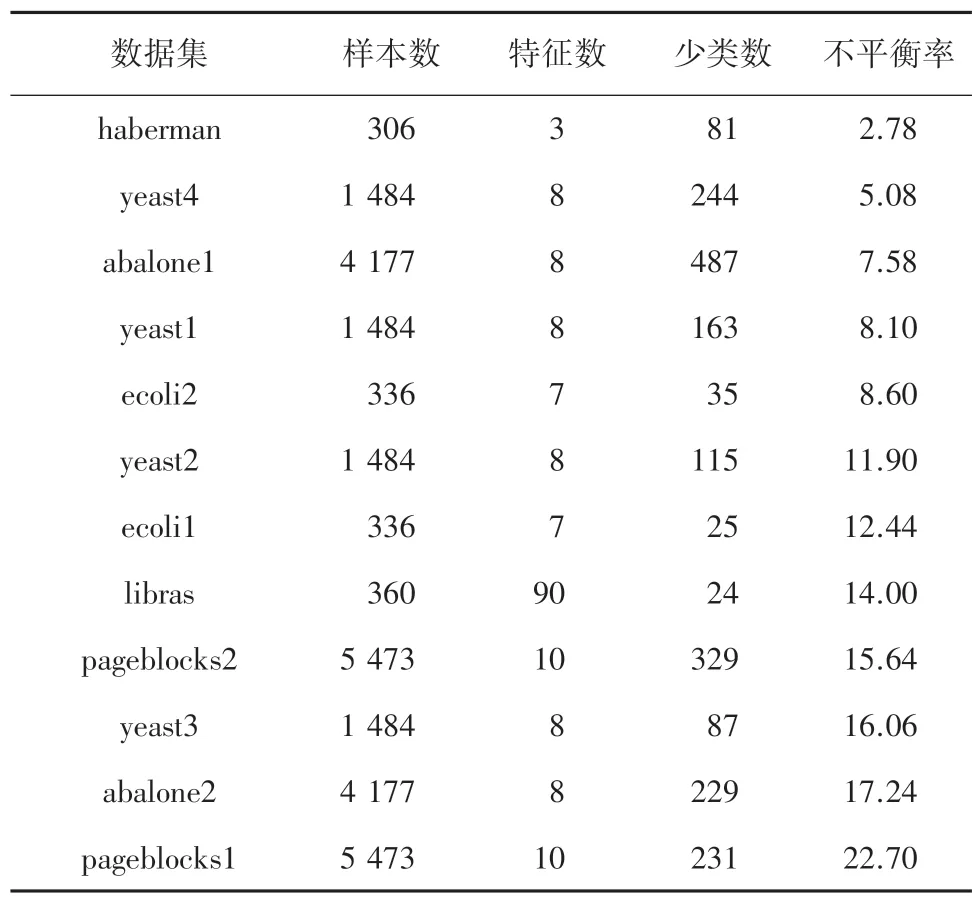
表1 数据集信息Tab.1 Information of the datasets

2.2 评价指标

在不平衡分类问题中，分类器通常偏向多数类样本，不能反映少数类的分类精度，而少数类的识别精度往往很重要，因此分类精度不适用于不平衡数据。和通常用来评价模型的性能，此处需涉及的数学公式可写为：

其中，表示预测和真实都为少类的样本数；表示预测与真实都为多类的样本数；表示少类预测为多类的样本数；表示多类预测为少类的样本数。

2.3 实验分析

为了验证本文提出的采样方法的有效性，将SMOTE、Safe-Level-SMOTE（SLS）、Borderline-SMOTE（BS）、ADASYN、CBSO 与本文提出的DPCOTE 算法进行了对比实验。此外，使用逻辑回归（LR）和支持向量机（SVM）两个分类器来验证DPCOTE 算法的泛化能力。所描述的实验均采用5折交叉验证，每组数据重复5 次，记录每个评估指标的平均值，以消除数据随机分组时可能出现的偏差。最好的结果以粗体字突出显示。每次实验都在2.9 GHz CPU、8 GB 内存的电脑上进行，软件环境是Python 3.7。其中，，是和的缩写。

表2 显示了使用LR 分类器，所提出的DPCOTE算法在和方面与典型对比算法之间的性能比较。由表2 可知，DPCOTE 算法的表现远远好于对比的过采样方法。具体来说，在指标方面，12 个数据集中，DPCOTE 算法有9 个数据集取得了最好的结果；在指标方面，有7 个数据集取得了最好的结果。

表2 在LR 分类器上的对比结果Tab.2 Comparison results on LR

图5 为使用LR 分类器，数据yeast4 在指标和上的箱线图结果，箱线图包括一个矩形箱体和上下2 条线，箱体中间的线为中位线，上、下限分别为数据的上四分位数和下四分位数，箱子的宽度可以体现数据的波动程度，箱体的上、下方各有一条线是数据的最大、最小值，超出最大、最小值线的数据为异常数据。从图5（a）中可以看出，虽然DPCOTE 算法数据波动较大，但数据的中值和上、下四分位数是优于对比算法的。在图5（b）中，DPCOTE 算法的中值和上、下四分位数是相对较好的，在箱体宽度方面，除了ADASYN 算法，DPCOTE 算法的数据波动优于其它方法，但是ADASYN 算法存在异常值。图6 为使用SVM 的可视化，结果显示DPCOTE 算法的中值和上、下四分位数是大于对比算法的。

图5 使用LR 分类器数据yeast4 的箱线图Fig.5 A boxplot using LR on yeast4

图6 使用SVM 分类器数据yeast4 的箱线图Fig.6 A boxplot using SVM on yeast4

为了全面对比本文提出的算法与其他采样方法在性能上的有效性，研究中使用了Wilcoxon 符号秩检验来评估DPCOTE 算法与对比算法之间是否有显著性差异。表3 为使用LR，SVM 分类器，在和的Wilcoxon 符号秩检验的结果，其中表示DPCOTE 算法的秩和，-表示相应对比方法的秩和。从表3 中可以观察到，在使用LR 分类器、显著性水平为0.05 的情况时，除了DPCOTE 算法与Borderline-SMOTE 在对比的值大于0.05 以外，大部分原假设都被拒绝，而且的值远大于-，说明DPCOTE 算法和其他采样方法相比有显著性差异。从表3 可以看出，在使用SVM 分类器时，DPCOTE 算法在和方面的表现好于对比算法。使用LR，SVM 分类器的Wilcoxon 实验结果见表4。使用SVM 分类器的Wilcoxon 检验的结果显示，除了DPCOTE 算法与Borderline-SMOTE 在下接受原假设外，所有的原假设都被拒绝，表明DPCOTE 算法显著优于其他对比算法。

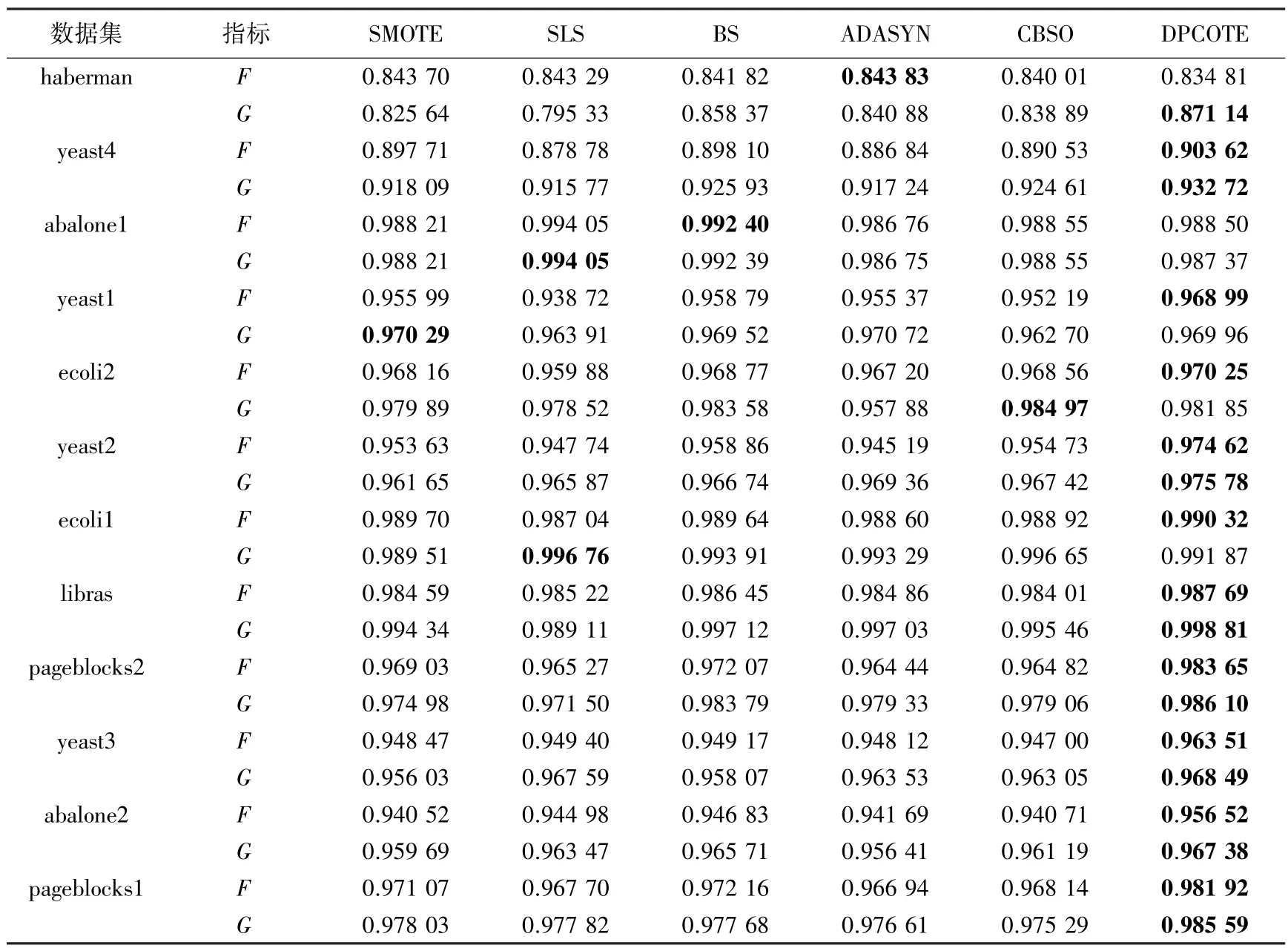
表3 在SVM 分类器上的对比结果Tab.3 Comparison results on SVM

表4 使用LR，SVM 分类器的Wilcoxon 实验结果Tab.4 Wilcoxon experimental results on LR，SVM

3 结束语

本文提出了一种基于密度峰值聚类算法的自适应加权过采样算法、即DPCOTE 算法来解决不平衡分类问题。DPCOTE 算法的基本思想为：考虑了类内不平衡问题，利用密度峰值聚类算法中的2 个重要因子，为每个少数类样本赋予采样权重，从而使每个少数类样本合成不同数量的新样本。同时，在DPC 算法中，引入马氏距离代替欧氏距离，消除特征间量纲不一致的问题。为了验证该算法的有效性，在和指标下，使用LR 和SVM 分类器进行了对比试验，且使用Wilcoxon 检验对结果进行分析。试验结果表明，DPCOTE 算法在12 个大小、不平衡率不同的数据集上取得了较好的结果。