桥面变形监测的多尺度分析与建立模型

汤同旭

(上海市测绘院，上海 200333)

0 引言

在桥梁的竣工、运营阶段，通过对桥梁的实际结构状态和环境变化的实时监测和结构性能的实时诊断，及时发现桥梁的变形趋势和尺度，评估桥梁安全性已经成为工程建设的必然要求。国内外针对全球导航卫星系统(Global Navigation Sa-tellite System，GNSS)变形监测数据的处理方法主要从时域分析、频域分析和时频域分析三方面展开。一般属于时域分析方法的有回归分析法、时间序列法、卡尔曼滤波法等，这些方法在过滤噪声提取趋势性信息方面具有优势，也在实际应用中发挥了重要作用。但这些方法对处理桥面数据均有线性、平稳性及标准性等要求，实际的桥面观测数据特别是影响因素复杂的桥面动态监测数据很难达到这些要求，将这类方法应用到桥面变形监测数据的处理，其效果将会受到很大的影响。

本文将引入经验模态分解(Empirical Mode Decomposition，EMD)方法结合奇异谱分析(Singular Sp-ectrum Analysis, SSA)方法处理钢箱梁桥面变形监测数据，以苏通大桥为例，利用GNSS接收机采集桥面动态变形监测数据，并对其监测数据进行处理与分析。其中数据采集使用徕卡Leica GS15接收机，可同时接收全球定位系统(Global Positioning System，GPS)/GLONASS/北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)信号，采样频率设置为1Hz，卫星截止高度角为15°，其精度可达厘米级，满足桥梁变形监测的数据精度指标。利用EMD方法对不同周期变形量提取的优势，可以将钢箱梁桥面的短周期变形量分离出来，对实验获取的钢箱梁桥面动态变形监测数据进行多尺度分解。钢箱梁桥面的短周期变形量一般与GNSS测量精度一致，且这种变形量是在外界环境的作用下产生的振动，很难将这部分变形量提取出来，通常视为噪声进行剔除。一般桥梁的振动频率可以表现出其自身的振动特性，如果桥梁的结构状态正常，那么其在各种环境因素的影响下的振动频率也比较固定。本文中采用EMD方法将桥面监测得到的GNSS数据分解为不同频率的本征模态函数(Intrinsic Mode Function，IMF)分量，分解后可以更加明显地得到IMF分量的振动特性，对于监测数据中频率信息的提取更加精确和有效。EMD分离出的IMF分量含有桥面原振动信号的频率信息，通过频谱分析方法可以将原信号各IMF分量的频率特征表现出来，进而识别出桥面监测数据中的振动信息。利用低频IMF和余项表示桥面监测数据中的长周期变形量，并且将它们作为去除噪声后的结果输出，结合SSA对去除的高频噪声进行降噪，从而完成对特长钢箱梁桥面的多尺度分解与重构。

1 EMD

EMD方法实质上就是对原始信号进行平稳化处理，依据信号的时间特征，对其进行自适应地多尺度分解。EMD方法理论上可以对任何信号进行自适应地分解，对于非平稳性、非线性信号的处理相比其他方法也有很好的效果，在实际工程应用中更具适用性。EMD的一般过程就是对原始信号的趋势或者波动进行逐级分解，因此可以得到若干个IMF分量与余项之和。IMF分量可以反映信号内部的特性，频率由高到低，高频IMF分量通常情况下为信号的噪声，分解后余项表示信号的趋势。EMD的基本理论与思想是，任何非线性、非稳定性的复杂信号都可以由不同的非正弦函数的分量组成。所以，对于原信号()，EMD可以将其分解为若干个满足以下条件的IMF分量：

1)待分解信号的极小值与极大值点数之和与过零点的个数之差不超过1；

2)极小值所构成的下包络线与极大值所构成的上包络线呈对称关系，对称轴为时间轴。

每一个IMF是待分解信号()经过EMD后得到的基本单元，图1所示为EMD的分解过程。

图1 EMD多尺度分解示意图

信号()分解后得到的所有IMF分量所有相邻零点之间只是一个单纯的波动，将信号()进行分解，可由式(1)表示

(1)

式中，()表示第个IMF分量；表示单调残差序列,一个典型的IMF分量如图2所示。

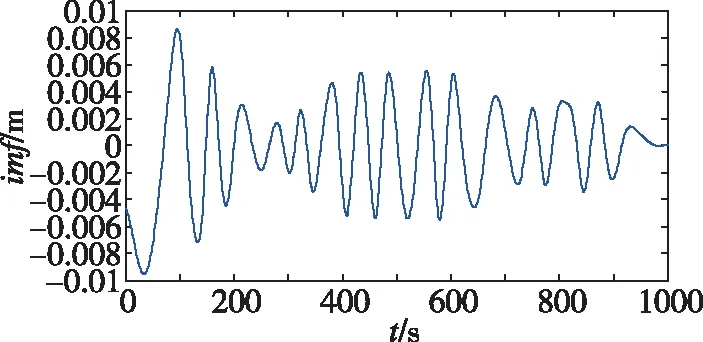
图2 一个典型的IMF

EMD方法的基本步骤如下：

1)找出待分解信号()的所有极大值序列和极小值序列，采用三次样条插值对极大值和极小值序列进行拟合，形成上、下包络线，上包络线记为()，下包络线记为()；

2)计算得到上下包络线的均值()

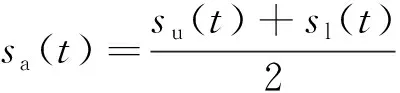
(2)

3)将原始序列()与上下包络线均值()作差，提取细节()

()=()-()

(3)

4)式(3)中，如果()的均值为零，那么()就是一个IMF，如果()的均值不为零,则需要对()重复进行上述步骤，直到()的均值为零时停止；

5)计算信号的残余分量

=()-()

(4)

若不是单调函数，即极值点的个数大于2，那么令=+1，继续以上的步骤；否则分解结束，即是残余分量。信号的重构过程也就是信号分解的逆过程，将所有的IMF分量和残余分量加起来就是原始信号序列()，如式(1)所示。

一般在信号水平一致的情况下，=时可以停止分解，但更多时候信号的噪声是未知的，因此要找到一个分解标准来确定合适的分解层数，从而达到较为理想的分解结果是非常重要的。依据相关的实践和研究，可以利用式(5)作为分解停止的标准，从而获取比较理想的分解结果

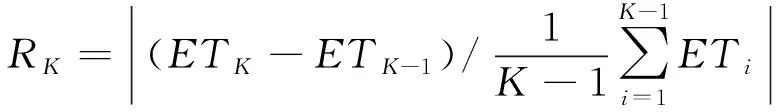
(5)

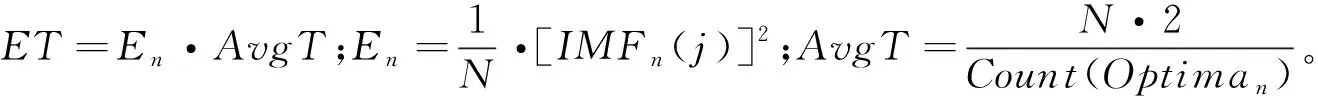
其中，()表示第个IMF分量的极值点的总数。

对于桥面GNSS变形信号,在利用EMD进行多尺度分解后，按式(6)定义标准化模量的累计均值(Mean Standardized Accumulated Modes，MSAM)

(6)

2 SSA

SSA方法结合常规时间序列分析、多元集合、多元统计、信号处理、动态系统以及奇异值分解(Singu-lar Value Decomposition，SVD)等技术，打破了传统的方法，是一类元参数、独立于模型的时间序列分析方法。它可以从监测序列中提取出主要的变形以及振动信息，进而方便对产生变形和振动的原因进行分析以及后续的预测预报。它的具体操作过程是：根据嵌入维数(即窗口长度)把样本量为的时间序列构造时滞矩阵，如果这个时滞矩阵能计算出明显成对的特征值，且对应的经验正交函数几乎是周期性或者正交时，就表明信号中有振荡行为。

假设一时间序列为,,…,，嵌入维数(即窗口长度)为(<2)，按照给定的建立时滞矩阵

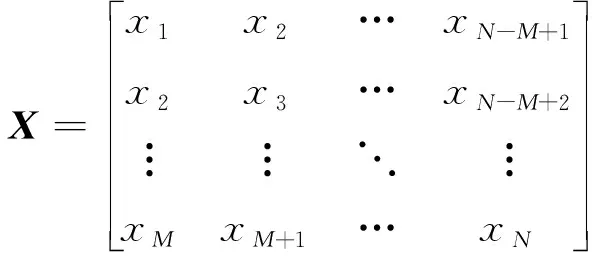
(7)

经过大量实验表明，当<3时，分析效果较为理想。时滞矩阵的第个状态量为

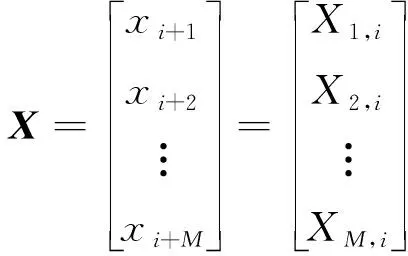
(8)

其中，=0,1,2,…,-。则时滞矩阵共有-+1个状态，对该时滞矩阵进行时间经验正交函数(Time Empirical Orthogonal Functions，TEOFs)展开(即对时滞矩阵进行SVD)，就可得到滞后自协方差阵

=

(9)

其中，()是时间序列时迟为(0≤≤-1)的自协方差，主对角线元素为时间序列的方差。用,,…,序列估计可得自协方差阵的元素()，即

(10)

式中，=0,1,2,…,-1。

自协方差阵是Toeplitz矩阵(实对称矩阵且主对角线为同一常数)。根据式(4)、式(5)可以求得的特征值和特征向量。

=(=1,2,…,)

(11)

自协方差阵的全体特征值为

≥≥…≥≥0

(12)

即为序列{}的奇异谱，将对它的奇异值运算的过程称为SSA。其中，对应的特征向量为第主分量(=1,2,3,…,)。第1主分量为信号最大的变化趋势，第2主分量为除第1主分量外剩余信号量的最大变化趋势…

计算状态量在上的投影,

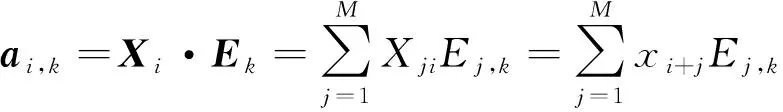
(13)

式中，0≤≤-；特征向量称为时间EOF(简称T-EOF)；,称为时间主成分(简称T-PC)。

SSA的重要功能由重建成分(Reconstruction Component，RC)实现。由T-EOF和T-PC重建一个长度为的序列，由第个T-EOF和T-PC重建的RC记为

,=

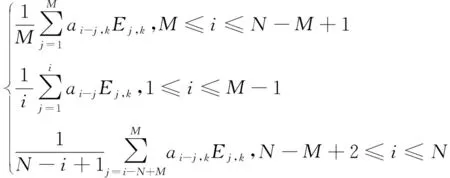
(14)

RC还具有叠加性质，所有重建成分叠加之和与原序列相同，即

(15)

在SSA中，利用Kendall非参数检验判断某一个RC是否为趋势项成分。具体过程如下(以判断第个RC是否为趋势项成分为例)：

1)计算满足<的指标数，并且构造统计量

(16)

2)若原假设：不是趋势项成分成立，服从均值为0、均方差为的正态分布。的计算公式见式(17)。

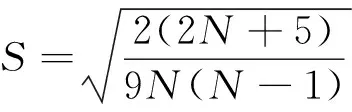
(17)

3)取信度=005，当<-196或>196时，则拒绝原假设，即认为第个RC为趋势项成分。>196时，第个RC呈上升趋势，<-196呈下降趋势。

3 EMD-SSA耦合模型

如上,结合EMD的自适应分解能力与SSA的降噪能力，提出了 EMD-SSA耦合模型。新模型通过对信号进行EMD后,可以得到一系列的高频IMF分量与低频IMF分量，并且对得到的IMF分量进行MSAM计算。对得到的高频IMF进行SSA降噪，很好地发挥了SSA的降噪能力。下面将给出该算法的具体流程以及评价指标，对信号处理的结果进行评价：

1)利用EMD方法对原信号进行分解，得到若干个具有不同频率的IMF分量，并且对IMF分量进行MSAM计算；

2)计算1)中分解得到的信号IMF分量的MSAM，并且对计算结果进行判断，如果在第层信号IMF分量的MSAM偏离零值，那么认为从第层开始所有的IMF分量表现为系统性误差，并且第1～(-1)层的IMF分量表现为高频噪声，此时可利用SSA对高频IMF分量进行进一步去噪；

3)重构经过SSA降噪处理的高频IMF分量和低频IMF分量，得到经过耦合模型重构后的信号；

4)通过给出的评价指标对分解重构后的信号进行评价，本文提出的EMD-SSA耦合模型示意图如图3所示。

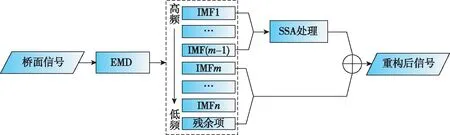
图3 耦合模型示意图

在钢箱梁桥面GNSS观测信号中，多路径信号存在周日重复的特点。从上述该模型处理步骤可以看出，新模型利用EMD方法对桥面GNSS信号进行分解，利用SSA方法对高频IMF分量进一步降噪，获取了高频IMF分量中的低频信息，最后可以获得桥面真实的振动信号。本文详细讨论了该模型削弱多路径误差与随机误差的方法与步骤，并给出了模拟实验和桥面GNSS信号处理的实际应用效果。

本文将采用偏差和相互关系数这两个评价指标对经模型处理后提取的桥面信号进行质量评价。

1)偏差(BIAS)

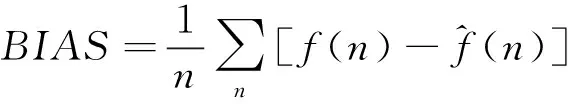
(18)

处理后的信号与原始信号偏差越接近零，表示处理效果越好。

2)信噪比(SNR)

信噪比是衡量信号中噪声量度的一种传统方法，作为评价去噪效果的指标，信噪比越大表示去噪效果越好。信噪比定义为

=10×log()

(19)

式中，为真实信号的功率；为噪声功率。

3)相互关系数()

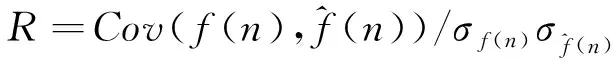
(20)

相关系数越大，表示处理的效果越好。

3.1 EMD-SSA耦合模型仿真实验

为了验证耦合模型处理信号的有效性，现模拟一个由3个不同频率的正弦信号的叠加数据，其函数为

=sin(2π1200)+sin(2π600)+
sin(2π300)+

(21)

模拟信号采样频率为1Hz，采样点数为4000个，是服从正态分布(0，15)的随机噪声，图4所示为真实信号和加了随机噪声之后的模拟信号。

(a) Real signal

将耦合模型应用于该模拟信号的信息提取，首先利用EMD方法对信号进行多尺度分解，如图5所示，余项的极值点与过零点相差1个时，停止分解过程，得到9个IMF分量和1个残余项，9个IMF分量从高频到低频依次排列，很好地分离出低频趋势项。

图5 模拟信号的EMD分解

3.2 高频分量SSA与信号重构

通过计算IMF分量的MSAM，从图6可以看出，IMF6分量的MSAM明显偏离了零值。同时IMF分量中包含有大量的频率信息，对IMF分量进行频谱分析，可以识别出模拟信号中的频率信息。采用快速傅里叶变换(Fast Fourier Transform, FFT)对EMD后的9个IMF分量进行傅里叶变换，将IMF分量转变为频域内的幅值。通过图7各个IMF分量的频谱图可以看出，每个IMF分量都有其在频谱图中的峰值点，峰值点对应的横坐标就是该IMF分量的主频。结合图6和图7，可以得到IMF1～IMF5为高频部分，主要为随机噪声；IMF6～IMF9和残余项主要为低频部分，表现为趋势项。

图6 模拟信号各IMF分量的MSAM

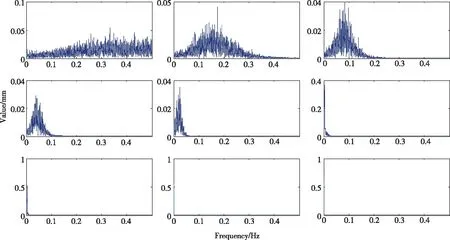
图7 模拟信号各IMF分量频谱图

对于IMF1～IMF5分量，采用SSA进行处理，根据嵌入维数和有效主分量层数的方法，可以计算得到嵌入维数为850，有效主分量层数为2。为了在IMF1～IMF5分量中尽量多地包含有效频率成分，选取IMF1～IMF5分量中有效主分量进行重构。将残余项、低频IMF和经SSA处理的信号进行重构，图8所示为经耦合模型提取后获得的信号，通过图8可以看出，总体提取效果较好。

(a) Extracted signal

为了解新模型对模拟信号特征提取的效果，表1分别给出了三种评价指标对不同方法下的模拟信号的特征提取效果。从表1中可知，新模型对模拟信号的处理效果最好，EMD方法对模拟信号的处理效果最差；再通过计算，相比EMD方法与SSA方法，新模型处理后信号的偏差分别减少了55.0%和40.0%，信噪比分别增加了21.16%和12.18%，相互关系数分别增加了2.4%和1.8%。综上所述，新模型对信号的特征提取是切实有效的，并且有着不错的效果。

表1 不同方法对模拟信号提取效果对比

4 钢箱梁桥面变形监测数据模型分析

由于受车辆荷载的影响较大，钢箱梁桥面的振动一般表现在其高程方向上，本文将采用苏通大桥GNSS监测点点、点与点高程方向上的GNSS变形监测数据进行新模型的趋势项提取，3个监测点高程方向上分别取1000个历元进行实验分析，单位为s。图9所示为跨中监测点点和桥面南北端监测点点、点高程方向上的监测数据时程曲线。从图9可见,在载荷变化和外界条件的影响下，跨中点位的高程变形量大多在-100mm～+100mm变化，点、点的高程变形量大多在-50mm～50mm变化，点的变形量受车辆荷载的影响较、两点大，在此仅以桥面跨中位置为例，进行相关问题的说明。桥面跨中位置的变形中包含量级较小的变形量，在新的模型中，首先利用EMD方法将这部分变形量从桥面监测数据中分离出去，这也是本文桥面监测数据多尺度分析的第一步。

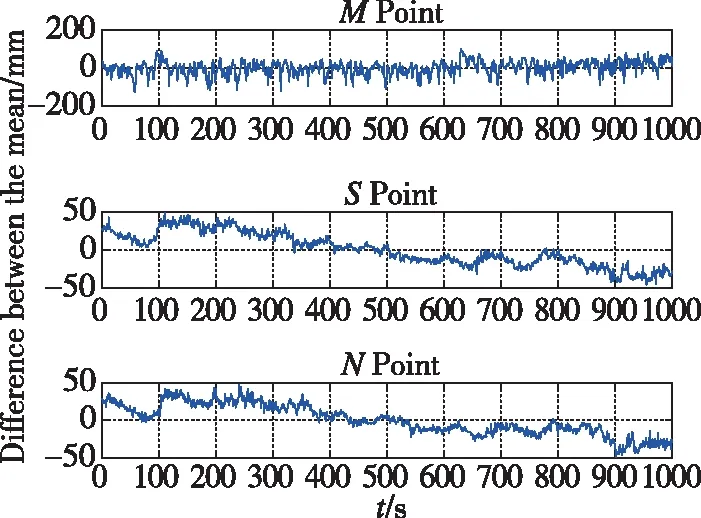
图9 桥面M、S、N点高程方向原始时间序列

利用EMD对桥面监测点GNSS数据进行多尺度分解，分解的结果如图10所示。通过图10可以看出，在分离出8个IMF分量和1个残余项后，分解停止，此时余项的极值点个数与过零点个数只差1个。可以看出，从IMF1分量到IMF8分量的频率一直在减小，但各分量的振幅却在逐级增大,一直到残余项趋于单调。各IMF分量的MSAM计算结果如图11所示。从图11中可以看出，第4个IMF分量的MSAM明显偏离零值，此时可认为IMF1分量～IMF3分量为高频分量，IMF4分量～IMF8分量与残余项为低频信息。

图10 桥面跨中监测点高程方向变形量EMD

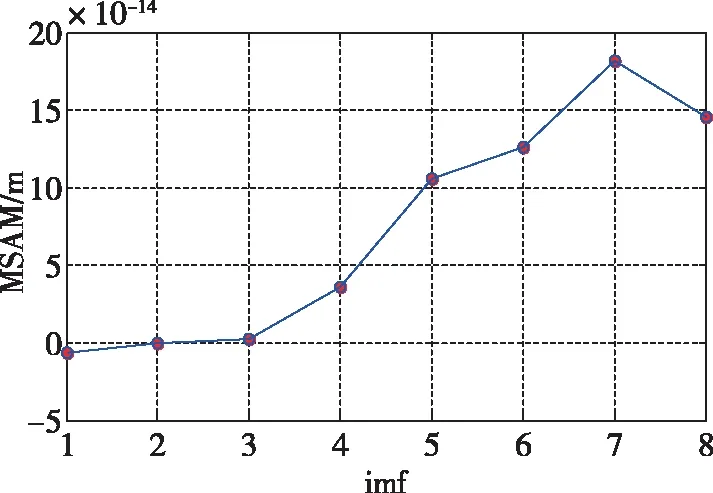
图11 桥面跨中M点高程方向各IMF分量的MSAM

4.1 IMF分量频谱分析与桥面振动分量提取

根据桥面跨中点的高程数据，对前8个IMF分量进行傅里叶变换，将时域内的IMF分量转变为频域内幅值随频率的变化。图12所示为前8个IMF分量的频谱图，各个IMF分量频谱图中峰值点对应的横坐标就是该IMF分量的主频。根据参考文献，苏通大桥一阶对称振动频率的理论计算值为0.180Hz，实测值为0.185Hz。根据图12频谱图对应的峰值，可以认为IMF1分量为含有振动成分的分量，提取振动分量如图13所示。同时IMF2、IMF3分量主要以多路径和随机噪声为主。

图12 钢箱梁桥面M监测点c1～c8分量频谱图

图13 钢箱梁桥面M监测点振动分量

计算含有振动分量的IMF1分量与含有多路径与随机噪声的IMF2、IMF3分量的相关系数，得到的结果为-0.0184，可以看出它们之间没有明显的相关性，表明通过EMD方法可以很好地将信号中的振动分量分离出来。本文采用EMD方法结合频谱分析的方法，识别出苏通大桥振动主频为0.184Hz，振幅达到了3.6mm。与《苏通大桥主桥斜拉桥动静载实验报告》中观测得到的结果进行对比，报告中主桥在满足最大工况的情况下，观测得到的主跨一阶振动频率为0.185Hz，并且振幅最大可以达到3.5mm，认为该方法可以有效地识别其主频，并且能够有效地分离出含有振动信息的变形量。

经EMD后IMF分量之间的正交性是评价EMD方法对信号处理结果的重要指标，IMF分量之间的正交性表明EMD的正确性，并且表明经EMD分离出的IMF分量之间是相互独立的。本文对苏通大桥桥面监测点变形监测数据进行EMD并对其结果进行分析，通过计算可以得到监测数据经EMD后各IMF分量之间的相互关系数，各IMF分量之间的相互关系数通过灰度表示。由图14可以看出，IMF1分量和其他IMF分量不具有明显的相关性，IMF1分量与其他分量相关系数都不超过0.02，IMF4～IMF8之间相关系数也不超过0.02，表明各分量之间相对独立，趋势项正交性明显，采用EMD方法对桥面监测信号进行分解取得了较好的结果。

图14 IMF分量之间相互关系数

4.2 高频噪声的SSA

进一步采用SSA方法对监测点观测信号IMF2～IMF3分量多路径误差高频噪声进行剔除，获得低频信号。通过图15可以看出，参照获取最优嵌入维数的方法，桥面监测点观测信号的IMF2～IMF3分量在=61处RC1-2重建序列与实际序列均方根误差(Root Mean Squared Error, RMSE)最小，所以可设窗口长度为61，此时的RMSE为0.5454。图16所示为桥面监测点高频IMF2～IMF3分量曲率谱图，根据图16可知，高频分量的信息主要集中在前4个奇异值上，所以有效分量层数为4。

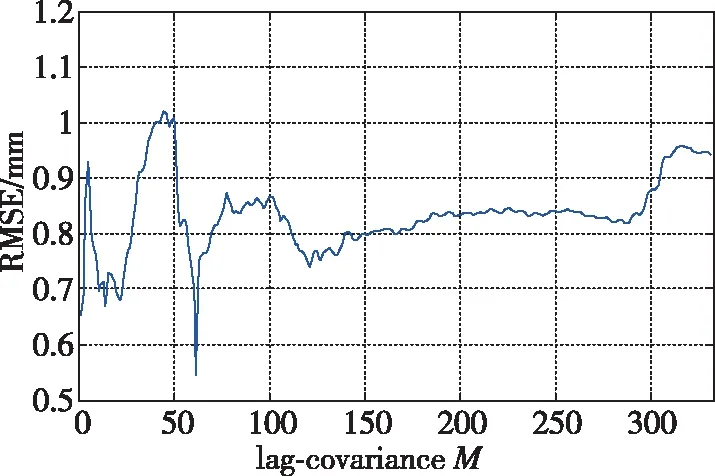
图15 桥面M监测点高频分量重建序列与实际序列均方根误差随窗口M的变化

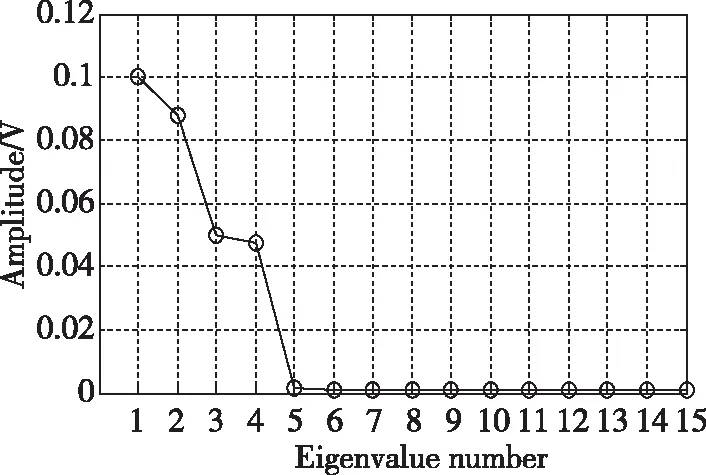
图16 桥面M监测点高频分量曲率谱图

对点IMF2～IMF3高频分量的有效主分量进行重建序列，图17所示为通过SSA方法点高频分量的有效主分量信号重建序列图，其中蓝线表示原始高频分量，红线表示高频分量降噪后的趋势成分。由图17可以看出，经过SSA重构后的重建序列比点高频分量序列更加光滑，表明SSA具有明显的降噪效果。

图17 桥面M监测点高频IMF2～IMF3分量有效主分量RC1-4信号重建序列

4.3 趋势项提取与变形分析

将经SSA去噪后的IMF2～IMF3高频分量与低频分量和残余项进行重构，重构结果如图18所示，图19和图20所示分别为桥面、两点经耦合模型处理后的重构结果。

图18 桥面M监测点高程方向经耦合模型处理后的重构信号

图19 桥面S监测点高程方向经耦合模型处理后的重构信号

为了验证新模型对于桥面监测信号的处理效果，表2～表4分别给出了新模型对于、、三点信号提取结果的几组评价指标。

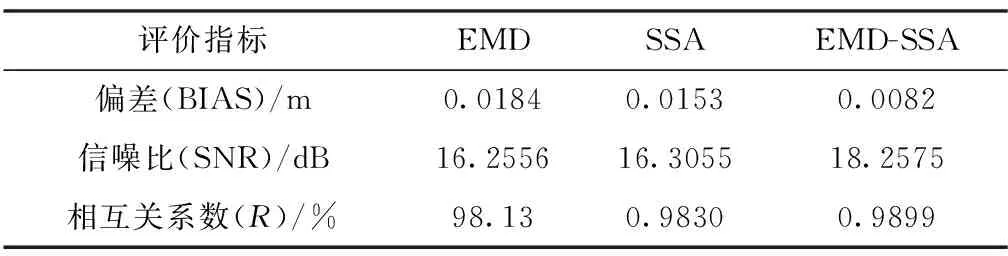
表2 不同方法对桥面变形信号提取效果对比(M点)

表3 不同方法对桥面变形信号提取效果对比(S点)

表4 不同方法对桥面变形信号提取效果对比(N点)

从表2～表4可以看出，不管是从偏差还是信噪比或是相互关系数的对比，SSA方法对于桥面监测点信息的提取都要优于EMD方法，但是新模型的信号提取效果相对于EMD、SSA方法更为显著。通过计算可知，对于点信息提取，新模型较EMD、SSA方法偏差值分别减少了55.43%与46.40%，信噪比分别增加了14.05%与11.97%，相互关系数分别增加了0.88%与0.71%；对于点信息提取，新模型较EMD、SSA方法偏差值分别减少了48.13%与18.56%，信噪比分别增加了10.31%与7.56%，相互关系数分别增加了0.82%与0.69%；同样对于点信息提取，新模型较EMD、SSA方法偏差值分别减少了41.14%与23.74%，信噪比分别增加了14.05%与13.47%，相互关系数分别增加了0.42%与0.40%。

经过模型重构得到的是长周期变形分量，即桥梁结构在外界荷载等变化下产生的趋势性变形。由图17可以得到桥面跨中高程方向上的动态变形量为-97mm～85mm之间，变化幅度达到了182mm。在《苏通大桥主桥斜拉桥动静载实验报告》中，苏通大桥在满载情况下跨中高程方向最大变形量为1388mm，远大于本文中苏通大桥跨中高程方向上的变化幅度，认为主桥在运营期内变形量在设计范围内。

5 结论

1)在EMD、SSA方法的基础上，提出了一种新的EMD-SSA耦合模型，首先通过仿真数据验证了该模型在信号提取中的优势，并给出了三种评价指标对不同方法下的模拟信号的特征提取效果进行对比。通过计算得知，新模型对模拟信号的处理效果最好，表明新模型对信号的特征提取是切实有效的，并且有着不错的效果。

2)对桥面GNSS监测数据采用新模型进行趋势项提取，首先探讨了桥面变形监测数据中包含的振动成分，得出桥面变形监测数据由噪声分量、振动分量和结构变形分量组成。结合频谱分析，得到EMD后的IMF分量的频域范围，有效地分离出含有振动信息的变形量，并且对EMD方法的相关性进行了分析，验证了EMD多尺度分解的正确性。

3)对经EMD 后的高频噪声分量进行SSA去噪，获得高频噪声中的低频信息，将经SSA去噪后的高频分量与低频分量和残余项进行重构，通过三种评价指标对不同方法的特征提取效果进行验证，同样与EMD、SSA方法进行对比，可得EMD-SSA耦合模型的效果最好。最后对重构的结构变形分量进行分析，得到桥面的振动信息和结构变形特征，与相关检测报告的结果相一致，验证了该模型的可行性。