捷联惯导准静基座大失准角线性初始对准方法研究

狄静波，常路宾

(海军工程大学电气工程学院，武汉 430033)

0 引言

初始对准是捷联惯导工作的起始和必要过程。常用的初始对准方法是传统的两步初始对准方法，即先利用解析方法进行粗对准，快速地获得概略已知姿态信息，进而利用该姿态信息作为初始值进行线性卡尔曼滤波精对准。如果能够获得较为精确的初始姿态，捷联惯导线性误差模型能够有效地完成各种条件下的精对准。由于在角运动/线运动干扰下，传统的解析粗对准不再适用。针对上述难题，目前有两类解决方案：一是利用人为定义惯性系作为过渡坐标系的优化对准方法；二是推导大失准角条件下的非线性误差模型，直接利用非线性滤波进行对准。优化对准是近年来较为盛行的初始对准方法，无论是在学术研究还是在工程应用角度都产生了较大影响。可以说，优化粗对准+卡尔曼滤波精对准能够解决绝大部分应用场景下的初始对准问题。而非线性初始对准一直尝试将传统的两步对准方案统一，直接实现一步对准。但非常可惜的是，由于非线性误差模型的固有缺陷，非线性初始对准在对准速度和稳态精度上一直没有达到传统的两步对准效果。很多时候，非线性初始对准仅仅是作为验证新型非线性滤波算法的一种算例，较少有研究涉及相关模型的优化改进。

近年来兴起的不变扩展卡尔曼滤波(Invariant Extended Kalman Filter，IEKF)算法在惯性基领域得到了广泛的应用，如姿态估计、同时定位与建图、视觉里程计等。不变卡尔曼滤波可以有效解决因状态误估计导致的系统可观测性与实际不符的问题。相关学者也将其引入到捷联惯性基组合导航、系统标定等领域，实验结果表明，该算法可进一步提高定位精度。不变卡尔曼滤波的优势在于通过定义在李群上的状态，构造相应的非线性误差量，进而推导出独立于状态估计值的线性状态空间模型。由于状态空间模型独立于状态估计值，因此能够做到“不变”，进而有效解决误差可观测性问题。独立于状态估计值的状态空间模型的另外一个突出优势是，基于该线性模型可以精确反推出李群上的非线性误差，即对于初始状态估计远远偏离真实值的情形，利用该线性模型同样可以做到滤波收敛。上述优势为利用线性误差模型实现大失准角初始对准提供了思路，即针对惯导初始对准应用场景下的惯导系统模型，能否推导或设计出独立于状态估计的误差状态空间模型。2015年,A.Barrau在其博士论文中首次报道了IEKF在惯导初始对准中的应用，相对于传统的初始对准方法，该线性化方法在大失准角下依然适用。

根据上述思路，本文利用李群理论中的仿射性分析方法，系统研究了准静基座条件下捷联惯导姿态和速度微分方程。分析指出，捷联惯导姿态微分方程满足仿射性条件，从而为利用其线性误差方程实现大失准角初始对准提供了可能。同时，通过分析(3)+和(3)两种状态描述下的误差模型，指出两种模型中速度误差模型都与状态估计值有关，而且(3)状态描述下的观测方程也与姿态误差有关。在上述分析的基础上，直接对(3)+状态描述下的速度误差方程进行改造，用重力矢量替换原有误差方程中的比力项，进而实现整体误差状态模型的不变性。仿真实验和车载晃动实验也验证了利用所研究的线性模型能够有效实现大失准角初始对准。

由于本文所研究的模型未考虑位置状态，因此只适用于准静基座条件下的初始对准；同时，状态空间模型未考虑惯性器件误差，因此所研究的对准算法仍然定位于粗对准。

1 准静基座下惯导模型分析

1.1 准静基座惯导微分方程

记地心惯性坐标系为系，载体坐标系(右-前-上)为系，导航坐标系(东-北-天)为系，地球坐标系为系。准静基座条件下，载体位置信息可以认为是已知且不变，因此对于粗对准而言，可以只考虑姿态和速度信息。导航坐标系姿态和速度微分方程为

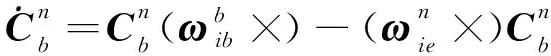
(1)

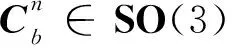
需要指出的是，式(1)中的惯导微分方程本质上是一个阻尼微分方程，即式(1)中已经默认代入了速度为零、位置为已知常值的条件。后续的线性误差模型都是在该阻尼惯导微分方程基础上推导的。因此，如果进行间接式初始对准，即先惯导解算、再滤波估计状态误差、进而反馈修正，那么在惯导解算阶段必须用该阻尼微分方程，而不能利用未简化的惯导微分方程。

1.2 惯导微分方程仿射性分析

根据李群理论，对于定义在群上的状态∈，其对应的状态模型为

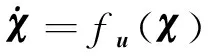
(2)

其中，表示已知输入量。文献[14, 18]指出，对于,∈，如果()满足如下关系式

()=()+()-

()

(3)

则()表示的模型是一个仿射模型，其欧几里得空间下的线性化模型独立于状态估计值，同时可以根据该线性化模型精确反推出李群上的非线性误差。

上述理论为利用线性模型实现任意失准角下的初始对准提供了思路，即通过对惯导微分方程中涉及的状态在李群上进行建模，进而分析其对应的模型是否满足上述仿射性条件。

对于模型(1)中的姿态和速度，一般有两种状态定义方式。惯导初始对准领域传统的定义方式为(3)+，即将姿态定义在李群上，而速度定义在欧几里得空间下。另外一种定义方式是将姿态和速度集成定义为特殊欧式群(3)的元素，即

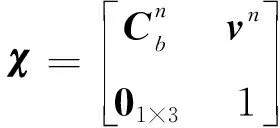
(4)

对于式(4)中的李群状态，其对应的系统模型为

()=

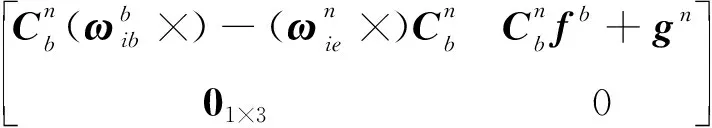
(5)

接下来分析模型(5)是否满足式(3)。根据定义(4)可得

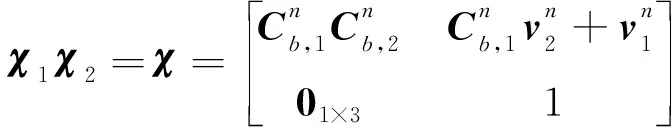
(6)

令=()，则

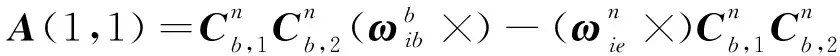
(7)

令=()，则

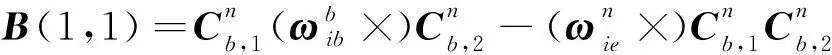
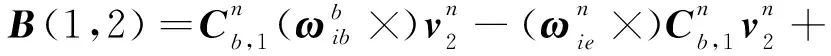
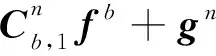
(8)

令=()，则

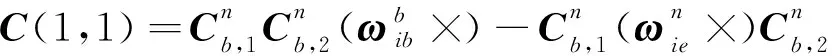
(9)

令=()，则

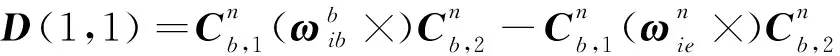
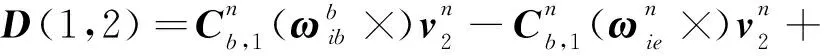
(10)

通过验证可知

(1,1)=(1,1)+(1,1)-(1,1)

(11)

但是由于

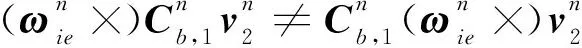
(12)

可以验证

(1,2)≠(1,2)+(1,2)-(1,2)

(13)

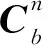
2 独立于状态估计的惯导线性误差模型设计

对于(3)+状态定义，定义状态误差量为

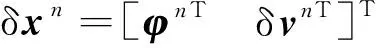
(14)

其中

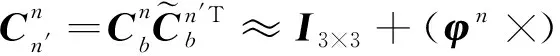
(15)

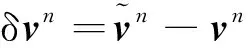
(16)

则δ所对应的状态空间模型为

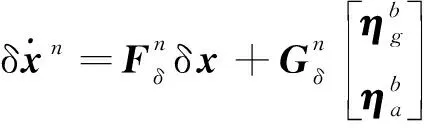
(17)

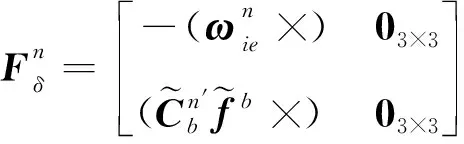
(18)

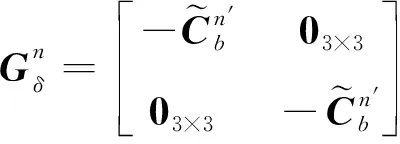
(19)

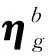
如果选取速度误差作为观测量，则对应的观测模型为

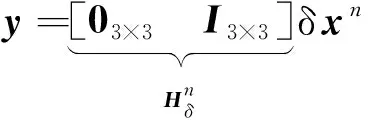
(20)

对于(3)状态定义，定义状态误差量为

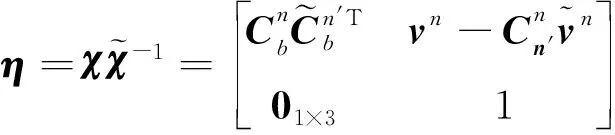
(21)

可以看出，姿态误差定义同式(15)是一致的。速度误差定义可近似为

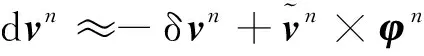
(22)

可以看出，式(22)中的速度误差与文献[15-18]中的变换速度误差是内在一致的，事实上，文献[15-18]中的变换速度误差也是受IEKF算法启发而来的。

定义状态量为

(23)

其对应的状态空间模型为

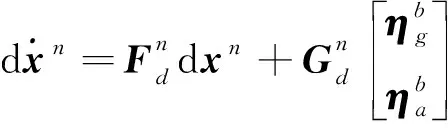
(24)

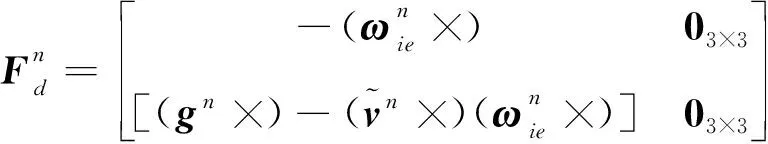
(25)

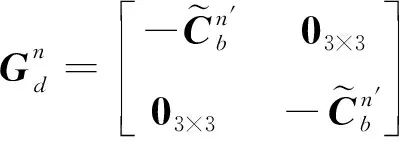
(26)

如果选取速度误差作为观测量，则对应的观测模型为

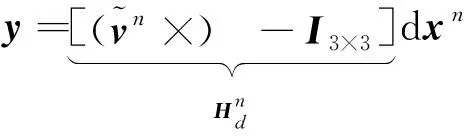
(27)

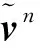
事实上，(3)+和(3)作为两种状态定义方式，在理论基础上并没有优劣之分，主要还是看基于其所构造的误差模型的呈现形式。文献[19]指出，状态误差量的构建并不拘泥于特定的流形上状态的定义。通过对比分析式(18)和式(25)可以看出，不同的速度误差定义可以产生不同的速度误差模型。由于姿态微分方程本身具有仿射性，其对应的姿态误差模型与状态估计无关。因此，可以对速度误差方程进行改造，目的是使其模型同样独立于状态估计，从而最大程度减小速度模型的非仿射性对整体系统误差估计的影响。基于上述认识，对状态空间模型(17)进行改造。在准静基座条件下，根据模型(1)可得

(28)

因此，式(17)可改写为

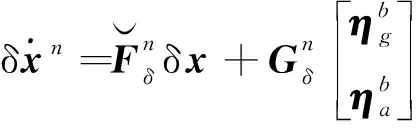
(29)

其中

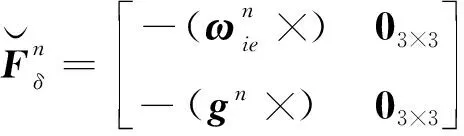
(30)

3 实验研究

为了验证所研究模型的有效性，分别设计了仿真实验和车载晃动实验。参与比较的算法模型分别为：状态空间模型(17)和(20)记为模型1；状态空间模型(24)和(27)记为模型2；状态空间模型(29)和(20)记为模型3。

3.1 仿真实验

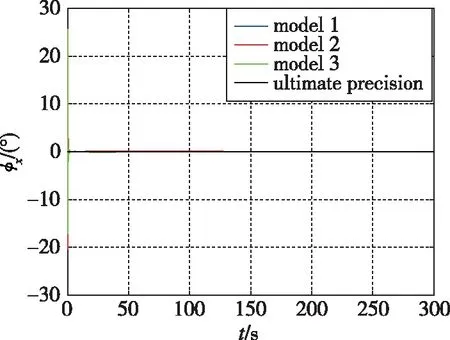
(a)

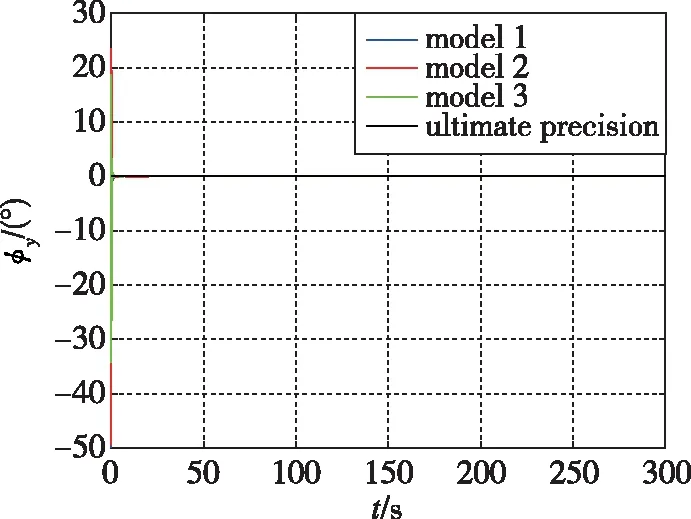
(a)

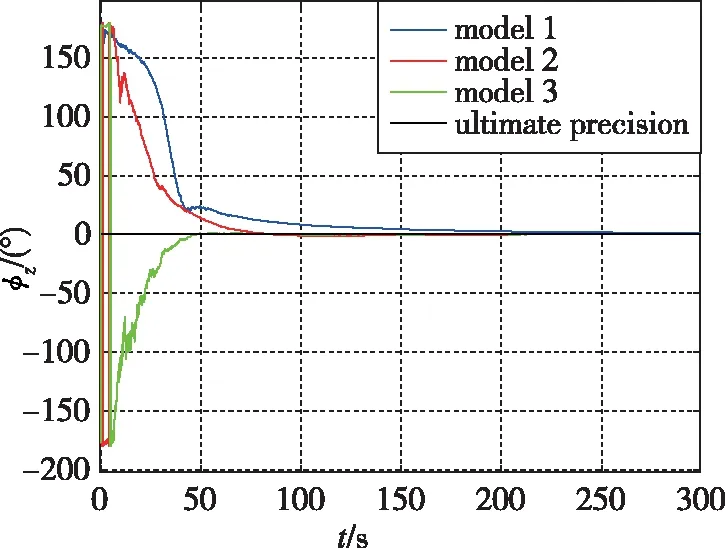
图3 仿真实验航向角对准误差

3.2 车载实验

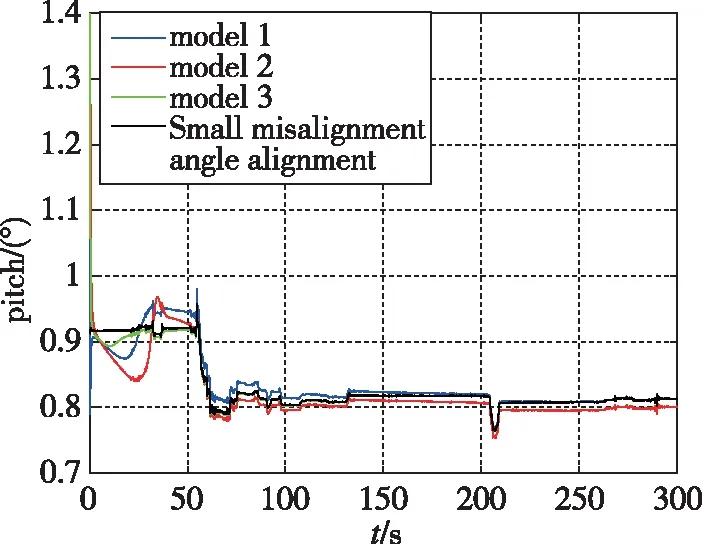
图4 车载实验俯仰角对准结果

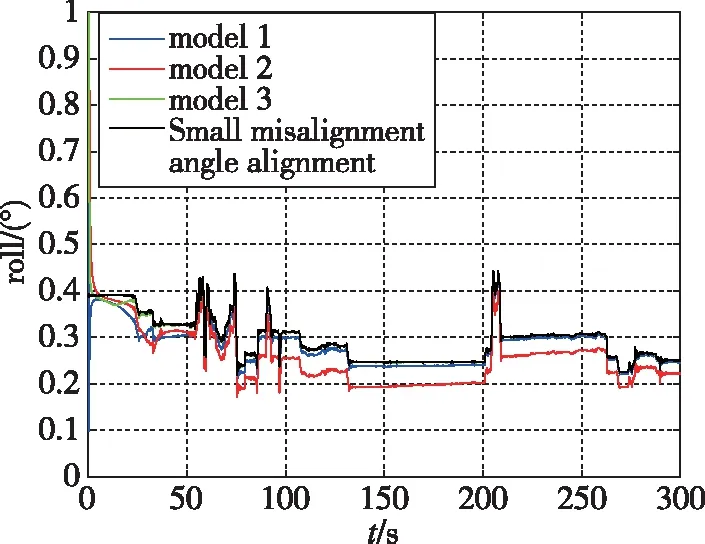
图5 车载实验横滚角对准结果

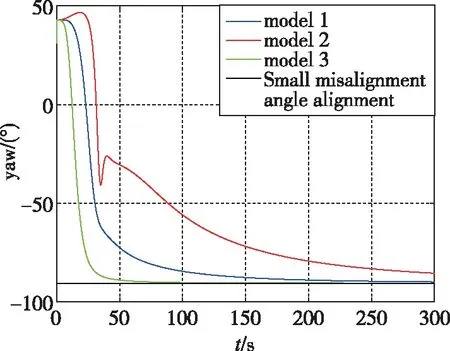
图6 车载实验航向角对准结果

4 结论

本文从仿射性分析角度,系统研究了准静基座条件下捷联惯导系统的初始对准问题。分析指出，惯导姿态微分方程满足仿射性条件，具备利用其线性模型进行大失准角初始对准的可能。但是当增加速度作为状态量后，整体模型不再满足仿射性条件，因此无论是基于(3)+还是(3)的状态描述，都不能直接推导出完全独立于状态估计值的状态空间模型。在上述分析的基础上，本文直接将(3)+状态描述下的速度误差模型中的比力项用重力矢量代替，从而构造出完全独立于状态估计值的状态转移矩阵。仿真实验和车载晃动实验结果表明，利用新构造的线性状态空间模型能够实现大失准角下的初始对准，初始对准速度和精度都优于传统模型。

基于本文的分析和实验结果，可以得到以下结论:

1)在准静基座条件下，采用优化对准或者本文提出的线性大失准角对准都能够较为准确地为后续卡尔曼滤波精对准提供初始姿态信息。

2)本文所研究的方法也能够为后续的线性卡尔曼滤波精对准提供姿态方差初始信息，从而缩短相应的阶跃响应时间。

由于本文的分析是在准静基座前提下展开的，相关模型和结论并不适用于动基座初始对准问题。由于增加位置作为状态后，会进一步影响模型整体的仿射性，如何参照本文思路推导独立于状态估计值的状态空间模型，进而实现动基座大失准角线性卡尔曼滤波对准是接下来需要开展的工作。

感谢西北工业大学严恭敏老师提供的开源高精度捷联惯导算法(Precise Strapdown Inertial Navigation System，PSINS)，相关程序代码加深了作者对惯导相关算法的学习理解，加快了对相关算法的改进和验证。感谢上海交通大学武元新老师在状态表示方面对作者的指导。同时，作者非常感谢严恭敏老师提供的车载激光陀螺惯导数据，该数据应用于本文中车载实验验证一节。