基于有限断层震源模型的北京地区强地震动模拟*——以1679年三河—平谷8级地震为例

巴振宁，赵靖轩，梁建文，张郁山，张玉洁

(1.天津大学 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室，天津 300350；2.天津大学 土木工程系，天津 300350；3.中国地震灾害防御中心，北京 100029)

0 引言

近年来全球发生的破坏性地震，如1994年美国Northridge地震、1995年日本Kobe地震、1999年土耳其Izmit地震、1999年中国台湾Chi-Chi地震、2003年伊朗Bam地震，均在近断层区域造成了大量的人员伤亡和建筑结构破坏(赵由佳等，2018)。其中Kobe地震造成了6 400多人死亡和接近1 000亿美元的经济损失，工业重镇神户和大阪遭受惨重破坏(Pitarka，1998)。近断层区域的严重震害促使研究人员开始重视这一区域地震动的研究，相关学者采用有限元(Hisada，1998)、有限差分(Rodgers，2019)、边界元(刘中宪等，2021)、谱元(Komatitsch，2012；Stupazzini，2009)等数值方法模拟了近断层地震动作用下复杂场地地面运动，试图预测未来发震断层附近的强地震动分布，为城市规划和结构抗震以及震害预防提供参考依据(李祥秀等，2021)。

北京作为中国的政治、经济和文化中心，其地位的重要性毋庸置疑。另一方面，北京坐落于典型盆地构造的范围内，具有发生大地震的构造背景。震害研究表明，沉积地形对强地震动有显著的放大效应(高文学，马瑾，1993)，从而对自振周期较长的高层建筑、大跨桥梁等建筑物造成比较严重的破坏(巴振宁等，2020)，给北京地区的经济发展和人民生命财产安全带来潜在威胁。

1679年三河—平谷8级地震是北京地区有历史记录以来最大的一次地震。据史料记载，此次地震由于震级较大、波及范围广、余震持续时间长，造成了大量的人员伤亡和财产损失(刘中宪等，2019)。其发震断裂(夏垫断裂)距北京市中心最近距离不到50 km，对北京地区建筑结构产生很大威胁(余中元等，2020)。众多学者对1679年三河—平谷地震进行了大量的模拟研究：高孟潭等(2002)采用有限差分方法，模拟的震源最高频率为1.6 Hz，震级为8.0，并着重研究了北京盆地对地震动的放大效应；朱耿尚(2014)采用有限差分法，模拟的震源最高频率为1 Hz，震级为7.7，并研究了沉积层分布对强地面运动的影响；付长华(2012)采用有限差分法，通过改变断层的埋深、倾向和滑动角等因素模拟了震级为7.5时的3～10 s长周期地震动，并研究了不同断层震源参数对盆地放大效应影响的差异；潘波等(2009)采用有限元法模拟得到的震源最高频率为1 Hz，震级为8.0，并发现三河—平谷地区出现比较明显的近断层效应和盆地效应。

但值得注意的是，1679年三河—平谷地震作为历史大震缺乏地震记录，难以进行震源破裂的反演，断层面上破裂细节尚不清楚(刘博研等，2007)。在模拟近断层地震动时，由于距离发震断层比较近，地面运动强烈依赖于发震断层面的位错发展过程、滑动方向和破裂速度等断层面上的破裂细节，断层面上破裂方式的改变影响了整个断层面上的破裂过程，从而对近断层地震动作用下地面运动分布有着不可忽视的影响(刘启方，2005；张效亮等，2018)。但在进行北京地区地震动模拟研究时，尚未针对断层破裂方式这一重要的震源条件对地面运动分布造成的影响进行分析，因此可能对强地面运动的空间分布以及峰值大小估计不足，从而影响城市规划和重大工程抗震设防。

基于以上分析，本文选取北京地区(39°30′～40°30′N，116°10′～ 117°20′E)作为研究对象，建立包含起伏地形的地下介质三维速度结构模型，并参考已有研究给出的断层位置、面积和倾角等震源基本参数建立确定性有限断层震源模型，开展了最高频率为2 Hz的确定性物理模拟。笔者在国家超算中心“天河一号”超级计算机上采用谱元法模拟了1679年三河—平谷8级地震作用下北京地区强地面运动分布特征，深入研究不同断层破裂方式(单侧破裂和双侧破裂)对北京地区强地震动的影响和可能引起的地震危险性分布特征，以期为近场复杂场地地震动估计和工程抗震设计等提供借鉴和参考。

1 确定性物理模型建立与参数设置

确定性物理模型的近断层地震动模拟精度和有效性取决于精细的三维速度结构模型(包含复杂场地条件)和合理的震源模型(张冬丽等，2009，刘启方等，2008)。为此，本文建立了含起伏地形的地下介质三维速度结构模型，通过地面高程数据和地下勘探资料，确定起伏地表及其下地层的空间分布。震源模型采用运动学震源模型，相关参数包括断层的形状、大小、位置等全局参数，以及断层面上的位错分布、破裂速度和破裂传播方式等局部参数。

1.1 运动学有限断层震源模型

运动学有限断层震源模型考虑为多个动态子源(点震源)地震反应叠加。建立有限断层震源模型时主要涉及断层面子源的划分以及断层震源参数的设定。主要思路是将断层面上每一块区域假定为由一个地震矩点源控制的子源。子源群中存在一个最开始破裂的起始点，其余每个子源的破裂起始时间由与起始破裂点的距离、传播方式以及时间过程确定。通过将所有子源的矩张量大小和对应的时间函数进行叠加，模拟整个断层面上的破裂过程。依据上述思路，笔者基于Matlab针对SPECFEM3D谱元程序开发了运动学有限断层震源模型程序，解决了谱元模拟中有限断层震源的输入问题，Matlab程序流程见图1。

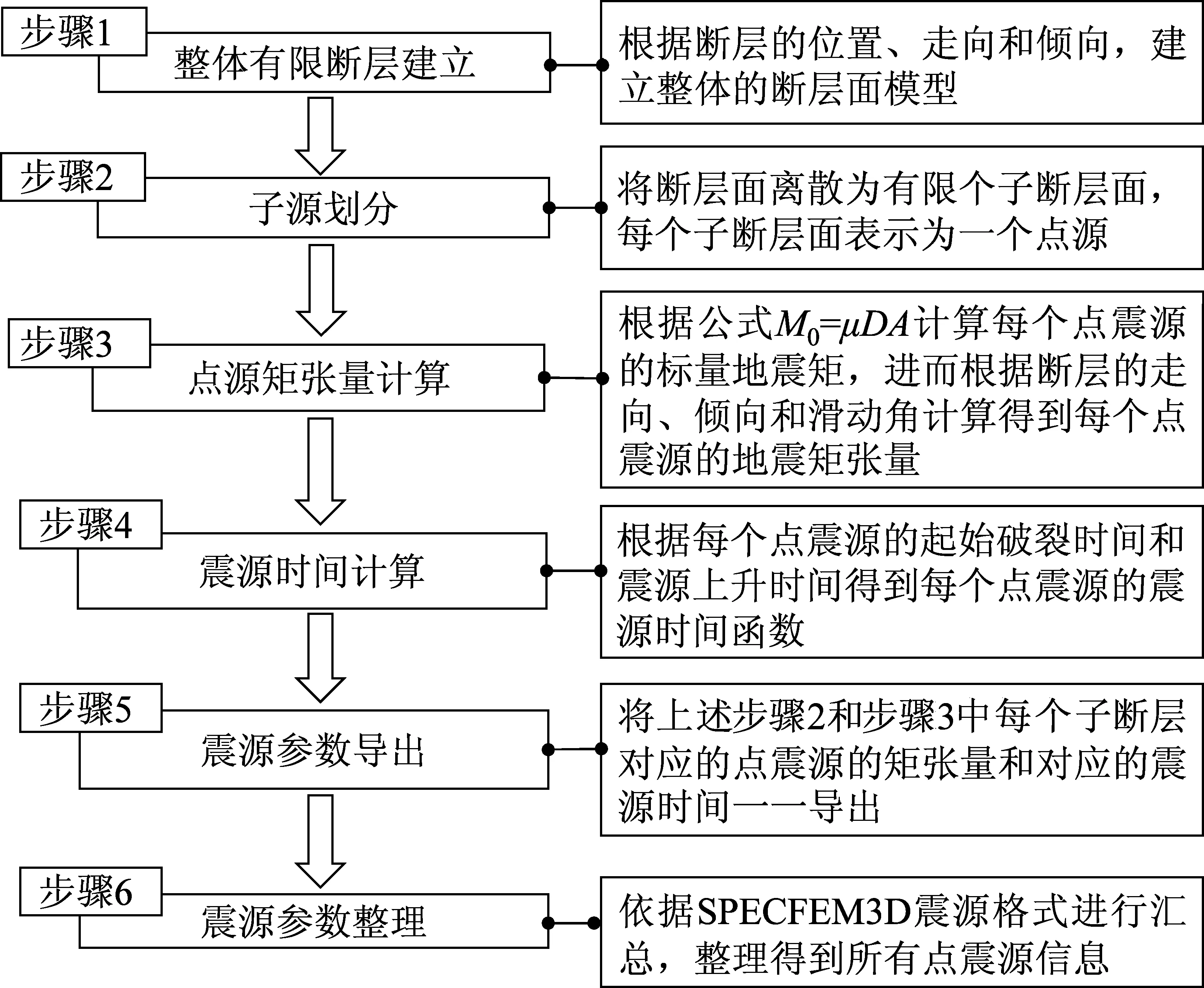
图1 有限断层震源设置主要步骤Fig.1 The main steps of finite fault source settings

针对三河—平谷地震建立确定性震源模型时，笔者首先根据历史考察资料进行全局参数的设置(表1)，然后使用高度约为1 km的三角形划分断层面，共划分为2 846个子源断层，进而进行局部震源参数设置，震源模型参考付长华(2012)提出的震源模型，断层面上设置两个凹凸体，其相对位置如图2所示。破裂面总面积为1 280 km，取22%为凹凸体的面积，取最大凹凸体面积为200 km，次级凹凸体面积为76 km。凹凸体中的平均滑移量为7 m，背景域的滑移量为2.3 m。并针对单、双侧两种破裂方式，共设置了3个震源模型，分别把震源破裂的起始点设置于断层面的中心和断层面左右边界的中心震源。

表1 断层震源参数设置Tab.1 Source parameter settings of the fault

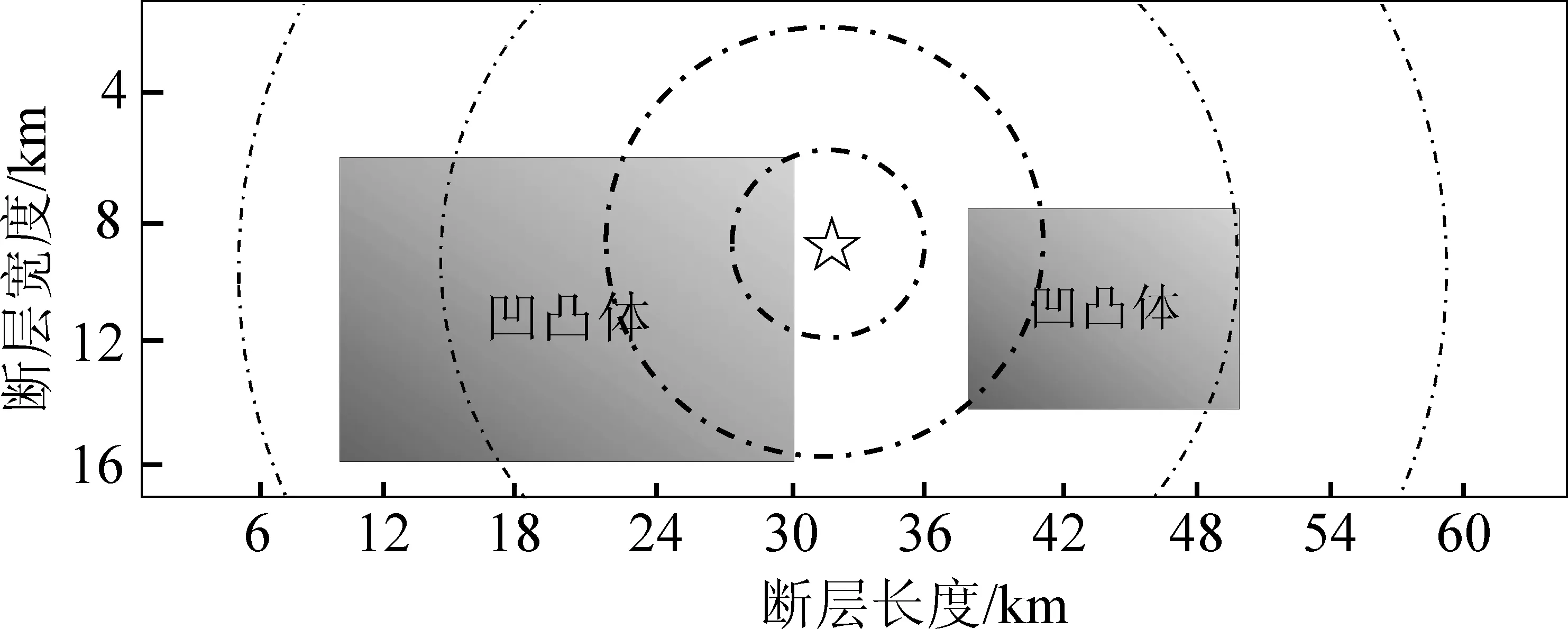
(a)断层面双侧破裂模型

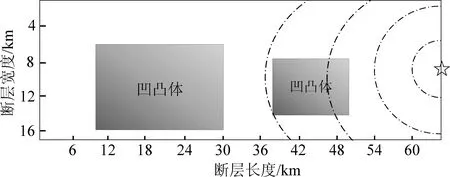
(b)断层面单侧破裂模型(破裂起始点位于断层左侧)

(c)断层面单侧破裂模型(破裂起始点位于断层右侧)图2 不同破裂方式对应的运动学有限断层模型Fig.2 Kinematic finite fault models corresponding to different fracture modes

1.2 三维速度结构模型

本文借鉴付长华等(2015)选择的区域范围(39°30′～40°30′N，116°10′～117°20′E)作为研究对象，根据地面高程数据、物探及钻孔资料，通过Csimoft公司开发的前处理软件Trelis建立含起伏地形的北京地区精细三维速度结构模型，模型东西长约120 km，南北宽约100 km，沿纵向深度约为40 km。模型包含地壳和上地幔顶部，被6个速度分层界面分割(图3a)，各个分层介质的物理参数见表2。

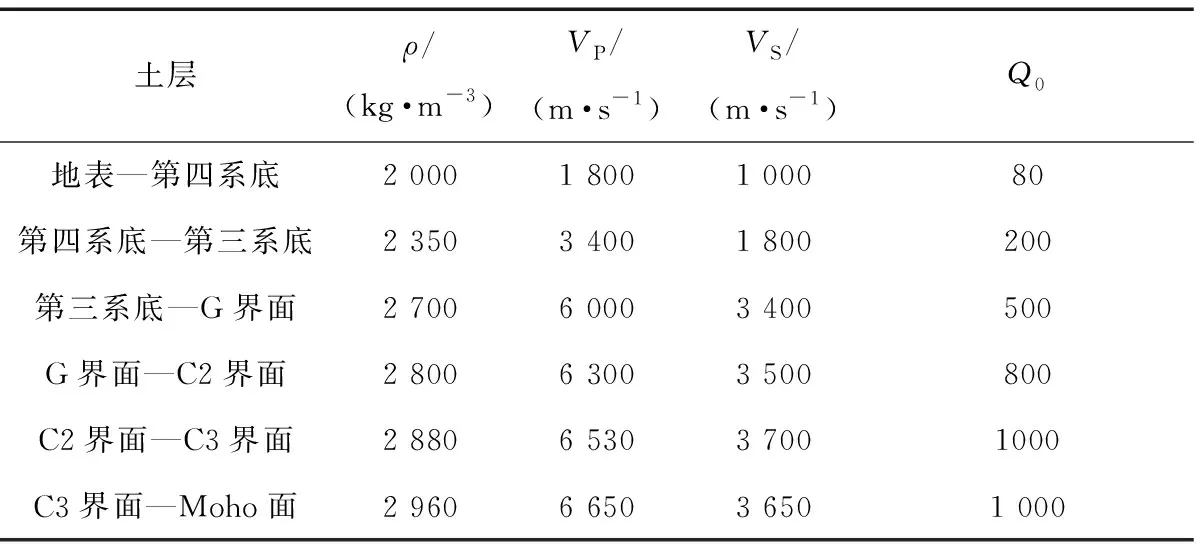
表2 北京地区各层介质的物理参数Tab.2 Physical parameters of the strata in Beijing area

建模时首先将地面高程数据和各个分层界面控制点的经纬度转化为平面直角坐标，然后依次将各个界面的控制点导入到Trelis建模软件中并将控制点扫掠生成各个分层界面，最后自上而下叠加所有分层界面，建立包含起伏地形的三维物理模型，如图3b所示。基于谱元法模拟时需要通过划分网格对整体三维模型进行离散，若将网格能传播的最大频率扩大一倍，则需要将网格间距尺寸减半，并且时间步长也随之减半，这就导致对目标地区的地震动模拟的计算量和计算时间显著增加。同时，为考虑地层实际情况，在进行三维模型建模时选择包含地壳和上地幔顶部等6个速度分层界面，模型的每个分层界面均为起伏面(图3)，这也为三维整体模型进行网格离散带来一定的困难。本文通过进一步减小网格尺寸，将设定模型网格能模拟的最大频率从1 Hz扩展为2 Hz。谱元法中为保证结果的精确可靠，要求最短波长中至少包含5个GLL积分点，根据实际地质介质参数，模型自地表至3 km深度处网格大小约为300 m，3 km至底部40 km深度处网格大小约为900 m，划分网格总数约270万，GLL节点数量约为2.23亿。

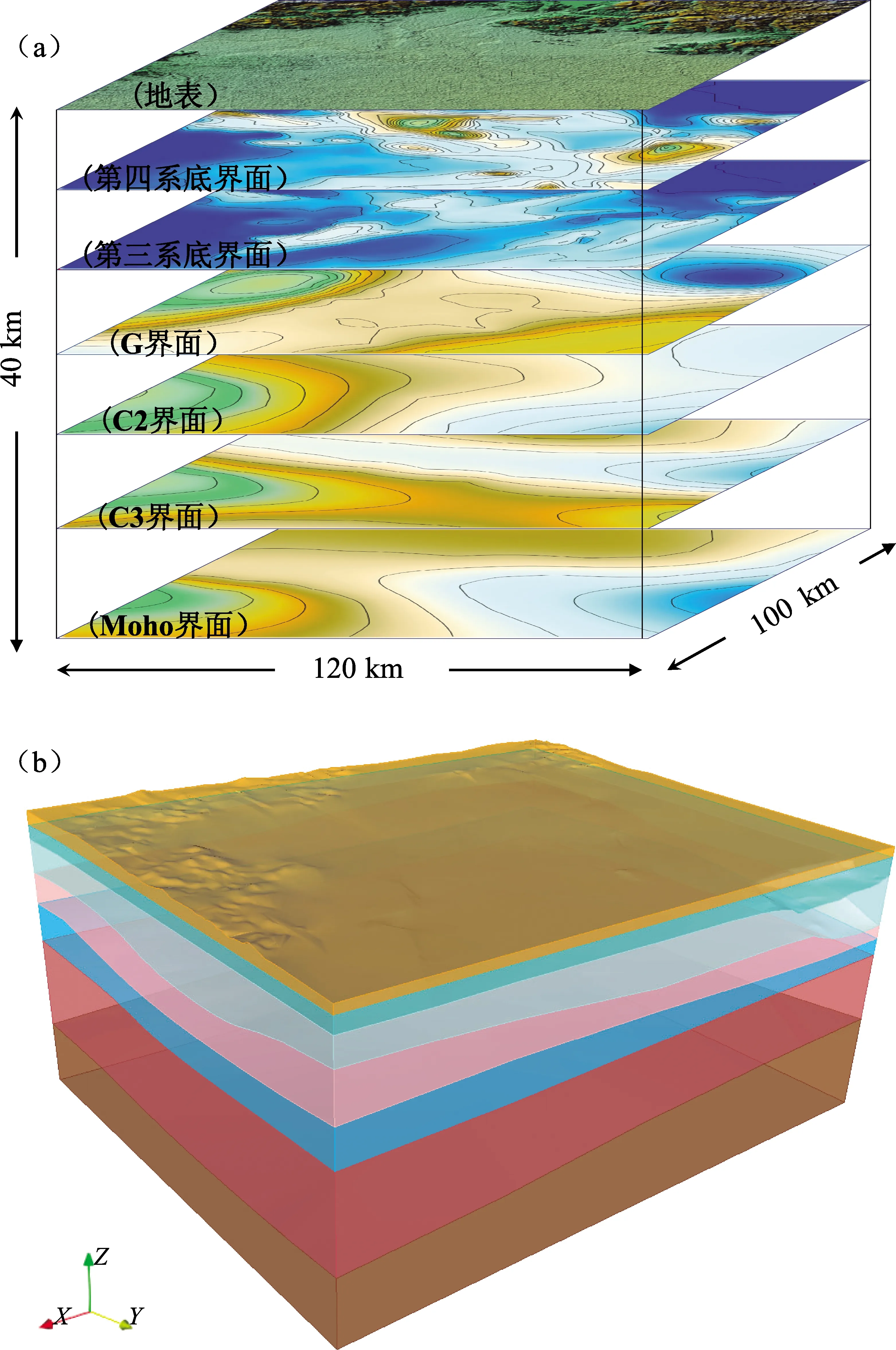
图3 北京地区地质构造界面(a)和三维速度结构模型(b)Fig.3 Geological interfaces(a)and 3D velocity structure model(b)in Beijing area

2 模拟结果及分析

计算时依次给出不同破裂方式下速度波场快照，峰值速度()分布，加速度、速度和位移的空间分布情况。计算任务基于国家超算中心“天河一号”计算平台，使用谱元程序SPECFEM3D，共调用200个进程计算，时间步距取为0.002 5 s，模拟90 s内的地震波传播，每种工况计算时间约4 h。

2.1 速度波场快照及其分析

图4给出了3种震源破裂方式下地面东西方向速度波场快照，图中五角星位置代表震源的起始破裂点，箭头指向为断层破裂方向。3种破裂方式波场快照图均从第5 s开始，并每隔10 s输出相应的波场快照结果。

从图4可以看出，不同破裂方式对应的地震波传播过程存在明显差异。双侧破裂的破裂起始点位于断层中间，波场表现为地震波自破裂起始位置向两端扩散的传播过程；单侧破裂的破裂起始点分别位于断层端部，波场相应表现出沿单方向传播的形态。对于3种震源破裂方式，震源破裂前方的地震动显著高于破裂后方，近断层的方向性效应十分明显。上述速度波场结果一定程度上证明了模拟结果的正确性和合理性。

图4 双侧破裂(a)、单侧破裂(左)(b)、单侧破裂(右)(c)3种震源破裂方式下速度波场快照Fig.4 Snapshots of velocity wave field in bilateral rupture(a)，unilateral rupture(left)(b)， and unilateral rupture(right)(c)modes

2.2 PGV云图分布及其分析

图5给出了不同破裂方式下地面水平方向分布图。图中显示3种情况下震中区域水平向处于2.3～2.5 m/s，地面分布情况与潘波等(2009)计算的北京地区的水平分布较为相符。强地面运动峰值分布的总体特征呈现“南强北弱，东强西弱”的趋势，断层迹线附近出现条带状集中分布特征。强地震动集中区的形状受到破裂方式的影响出现明显差别，双侧破裂引起的强地面运动水平分量在断层两侧的分布形态更为狭长，单侧破裂下分布形态相对更为集中。与单侧破裂相比，双侧破裂产生的强地面运动分布范围更广，模拟出的高烈度区范围明显扩大，尤其北京市区、大兴地区在双侧破裂情况下，水平可达到1.0 m/s，明显高于单侧破裂情况。

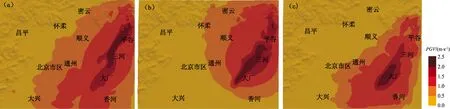
图5 双侧破裂(a)、单侧破裂(左)(b)、单侧破裂(右)(c)3种震源破裂方式下PGV分布Fig.5 PGV distribution in bilateral(a)，unilateral rupture(left)(b)， and unilateral rupture(right)(c)fault modes

上述现象的出现主要由于不同断层破裂方式下，破裂起始点和破裂方向的改变产生的断层破裂方向性效应与深厚沉积地形对地震动相互作用机制的结果。由于北京地区第四系主要发育于平谷、大厂和顺义等几个凹陷处，其中顺义和大厂凹陷第四系厚度为800 m，平谷凹陷的第四系厚度也超过400 m，不同破裂方式下地震动传播过程中受到沉积地形的影响，产生了地震能量迁移的现象，导致地震动响应被明显放大，强地震动的分布范围以及地震动峰值大小出现明显差异。

2.3 地表地震动时程及其分析

为进一步研究不同震源破裂方式对地震动空间分布的影响，选取北京市区、大厂等11个观测点，给出了不同震源破裂方式下各个观测点水平方向和竖直方向的加速度、速度和位移结果(图6)以及各个观测点对应的峰值结果(表3)。

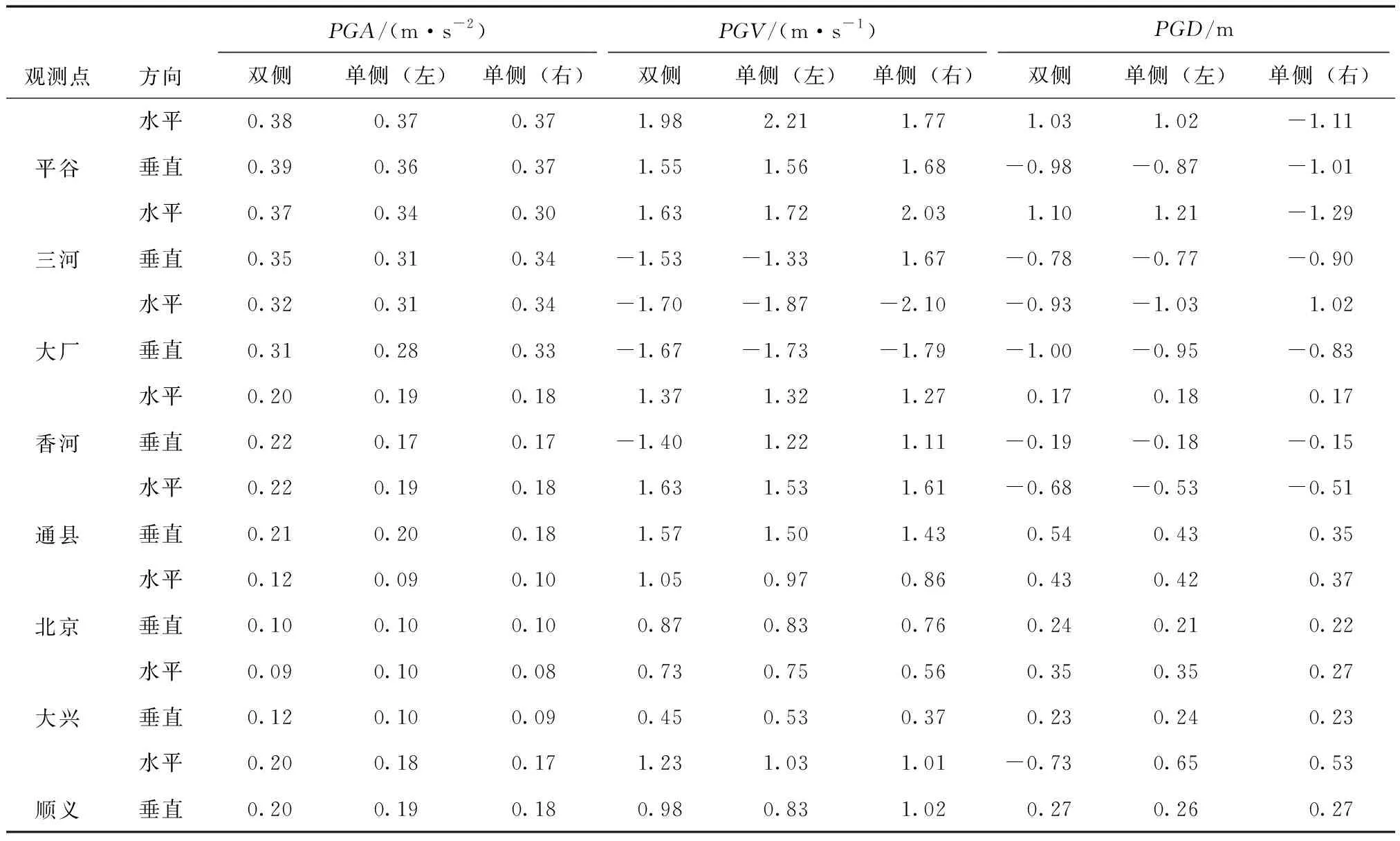
表3 不同破裂方式下不同观测点的PGA、PGV、PGDTab.3 PGA，PGV and PGD values corresponding to fault-rupture modes at different observational sites

2.3.1 近断层地震动效应

本文模拟结果很好地反应了近断层地震动特性，以双侧破裂情况为例，各个观测点地震动时程结果(图6)表明：①近断层集中性效应显著，强地震动主要集中在沿断层两侧一个狭窄的范围内，其中平谷地区水平和垂直向最大分别为0.38和0.39 g，三河地区水平和竖直向最大分别为0.37和0.35 g，随着断层距的增加，观测点的迅速衰减，昌平地区的约为0.02 g；②近断层速度大脉冲现象显著，靠近断层位置的三河、平谷等地区均出现了速度峰值大、持时短的速度脉冲现象，其中平谷地区水平和竖直向的达到1.98和1.55 m/s，三河地区水平和竖直方向的达到1.63和1.53 m/s；③断层破裂造成地面的永久变形现象显著，在靠近断层的位置变形也相对明显，以平谷地区为例，模拟中水平达到1.03 m，永久位移达到0.45 m。

2.3.2 不同破裂方式对地震动时程的影响

从图6还发现断层破裂方式显著影响了观测点的地震动时程结果，尤其是在靠近断层观测点出现了明显的差异。以大厂观测点的地震动时程结果为例，单侧破裂(破裂起始点位于断层右侧)时峰值出现的时刻最早并且水平和竖直向分别为0.34和0.33 g，高于双侧破裂时的0.32和0.31 g以及单侧破裂(破裂起始点位于断层左侧)的0.31和0.28 g；对比不同破裂方式的时程结果发现，断层破裂方式对速度时程结果的影响最为明显，以大厂观测点处水平和竖直向速度为例(图7)，破裂起始点位于断层右侧的单侧破裂情况下，大厂地区的水平和垂直向分别为2.10和1.79 m/s，地震动持续时间为45 s，地震动峰值和持时均明显高于双侧破裂情况和破裂起始点位于左侧的单侧破裂情况。上述现象在断层距较近的观测点，如三河、平谷和通县等地比较明显，在断层距较远的位置如怀柔、昌平等地不同破裂方式产生的地震动时程则差异不大。

图6 不同观测点对应的加速度(a)、速度(b)、位移(c)时程结果Fig.6 Time histories of acceleration(a)，velocity(b)，and displacement(c) corresponding to observational points

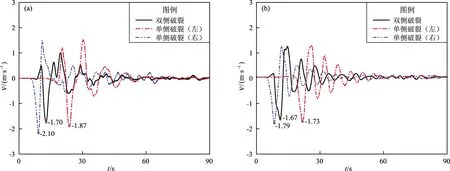
图7 不同破裂方式下大厂观测点水平(a)、竖直(b)方向速度Fig.7 Velocities in horizontal(a)and vertical(b)direction in fault rupture modes at Dachang observational site

出现上述情况的原因可能是：①震源破裂方式的不同导致各个观测点的震中距不同。当震源的破裂速度一定时，观测点震中距越近，地震波传播至各个观测点的时间越早，出现峰值时刻的时间越早。从图6观察发现，震中距越小的观测点如三河、平谷和大厂等，在不同破裂方式下峰值时刻差异明显；②震源破裂方式影响了地震动峰值大小和地震动持时，由于震中距的差异，导致近场上覆土层对于近断层地震动的衰减效果不同。当观测点距离震源中心较近时，松软土体对地震动的衰减效果不明显，导致该破裂方式下地震动峰值较高。特别是当区域内存在较厚沉积地形时，由于峰值时刻出现时间早、峰值较大且沉积地形对地震动的聚集放大效应，导致地震动衰减的时间明显延长。通过上述分析可以判定，断层震源的破裂方式与近断层区域内强地面运动密切相关。

3 结论

本文采用谱元法对1679年三河—平谷8级地震进行了模拟，通过改变断层面的不同破裂方式(即单侧破裂和双侧破裂)，得到了不同破裂方式下地面的速度波场快照、分布图和地震动的空间分布结果，通过对这些结果进行分析得出以下主要结论：

(1)北京地区强地面运动分布体现了条带状集中性分布特征、方向性效应以及永久位移等近断层地震动特性。北京地区强地面运动峰值速度分布呈现“南强北弱，东强西弱”的趋势。三河—平谷地区最高可达0.37 g，大厂地区最高可达0.32 g，表明平谷、大厂等地区为震害分布的主要区域。

(2)断层破裂方式显著影响了北京地区的地面运动分布情况，根据分布图发现双侧破裂比单侧破裂影响的范围更广，北京地区遭受地震灾害的威胁最大。

(3)不同断层破裂方式对近断层区域内的地震动时程结果也存在较大影响。以大厂观测点为例，由于震中距不同，在不同破裂方式下地震动时程表现出的峰值时刻、峰值大小和地震动持时明显不同，尤其当观测点处存在沉积地形时该现象更为明显。

本文通过精细化地质模型建模以及不同震源模型的输入，模拟得到了北京地区的强地面运动分布，上述模拟结果可以为北京地区震害预测预防和建设规划提供一定的指导和借鉴。

感谢中国地震局地球物理研究所付长华博士提供的北京地区地质勘探资料，感谢国家超级计算天津中心“天河一号”为本文计算提供的帮助。