一种基于曲波域的压缩感知降噪方法及其在水库气枪信号中的应用*

2022-06-23杨润海张惠菊沈娅宏

地震研究 2022年3期

张帅，杨润海，张演，张惠菊，姚远，沈娅宏，李平

(1.云南省地震局，云南昆明 650224；2.开远市地震局，云南开远 661699)

0 引言

利用地震波研究地球内部介质变化依赖于重复性震源，使用天然重复震源进行介质变化测量的时间、空间分辨率及精度都受到一定程度的限制，而大部分人工震源监测研究主要集中于浅层地壳(王宝善等，2016)。近年来，利用气枪重复震源研究地球深浅部结构和介质变化成为一种有效手段。大容量气枪震源与其它震源相比，有着激发性能高、低频成分丰富、可重复性好、绿色环保、安全效能高等特点(Wang，2016，2020；Chen，2017；陈颙等，2007；王伟涛等，2017)，应用前景十分广阔。

在气枪源探测过程中，地震波速变化测量本质是要解决数字信号处理的时延估计问题，其中信噪比是影响信号波速测量精度的关键(杨润海等，2020；蒋生淼等，2017)。而实际地震记录信号由于存在随机干扰和能量衰减，具有一定的非平稳性，同时气枪震源能量有限，传播距离较远时信号信噪比低，甚至难以辨认(向涯等，2019；李孝宾等，2017；徐逸鹤等，2016)。在波速变化的计算过程中，为了提高信噪比，通常会对信号进行滤波和叠加等处理(刘自凤等，2015；叶泵等，2017；谭俊卿等，2020；Xiang，2019)，但由于部分台站距离太远，有效信号往往湮灭在噪声之中，利用传统降噪方法处理后的信号信噪比仍然较低，导致波速变化的计算结果误差较大，甚至不能反映真实的介质变化情况。因此，运用新的降噪方法压制噪声，仍是提高地震资料信噪比和增强信号测量精度的主要途径。

曲波变换是一种能够对信号进行最优稀疏化变换的方法，它是通过基函数与信号的内积来实现信号的稀疏表示(Candes，Donoho，1999；Candes，2005)，具有多分辨率特性、时频局部性、多方向性等优点，克服了小波变换表示边缘、轮廓等高维奇异时的局限(Herrmann，Hennenfent，2008；仝中飞等，2008)。由于有效信号通过曲波变换后的曲波系数是稀疏的，而噪声信号是随机信号，在曲波域中的系数表现为非稀疏性。有效信号受到噪声影响时，在曲波域中的稀疏性降低。传统的曲波降噪方法是通过设定软硬阈值进行滤波，大于设定阈值的系数保留，小于阈值的去除，但如果阈值设置过大，在连续处容易造成不光滑的伪影或者伪吉布斯现象，而阈值设置过小，噪声压制能力减弱，将会严重影响信号的降噪效果(刘磊等，2011，王文波等，2006)，因此在曲波域中引入全变差技术通过调整域中大小系数，再进行阈值滤波，可以使原始信号的主要特征得到保持(唐刚，杨慧朱，2010)。

为了重建曲波域中由于阈值的设定导致系数过度缺失，造成信号关键细节随机丢失的问题，本文引入压缩感知理论。压缩感知理论是由Candes等(2006)正式提出(Hennenfent，Herrmann，2008)，随着近几年的不断发展，已经成功应用于多个地震学和地球物理反演问题中(张帅等，2021；唐刚，2010；姚华建，2013；Yao，2011)。压缩感知数据重建过程涉及稀疏变换、采样方法(测量矩阵)和重构算法，大部分研究都是基于这3个方面开展(Yin，2014)。传统地震数据重建方法大都受 Nyquist采样理论的限制，对于不满足采样定理的超稀疏地震数据，重建效果不佳(郭念民等，2014)。而压缩感知理论表明：即使是随机缺失的数据，也可以恢复出满足一定精度要求的完整数据(唐刚，杨慧朱，2010；孔丽云等，2012，白兰淑等，2010)。因此利用压缩感知信号重建方法，可以解决因阈值选取不当导致信号曲波域中重要系数缺失的问题，最大程度地重构出有效信号的系数。

如上所述，综合两种方法的优势，本文构建了一种基于离散曲波变换的压缩感知方法，将曲波域中的阈值滤波和全变差技术与压缩感知正交匹配重构算法(OMP)的稀疏促进策略充分结合起来，对有效信号和噪声信号进行有效分离，从而实现信号的高效降噪目的。

1 研究方法原理

1.1 曲波变换

信号的稀疏表示至关重要，离散余弦变换、小波变换、曲波变换等都能稀疏表征信号，因此常常被用作压缩感知的稀疏变换基。曲波变换具有各向异性和多尺度、多方向的诸多优点，较其它2种方法稀疏效果更好(Herrmann，Hennenfent，2008)，是地震数据稀疏表达最有效的方法之一，用离散曲波变换来稀疏表征地震信号的方法原理如下：

假定输入信号为[,]，其中≥0,<，<，基于wrapping算法核心思想：围绕原点包裹，对任意区域映射到原点的仿射区域(杨连刚等，2019)，其具体变换流程如下：

①将[,]通过二维的傅立叶变换和FFT域采样得到表达式为：

(1)

②每个尺度和角度与窗函数作用后得到：

(2)

③对于每一个大小为×的窗数据，围绕其原点，可得：

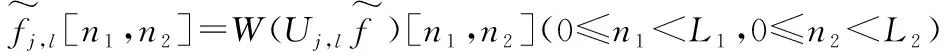
(3)

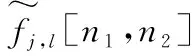
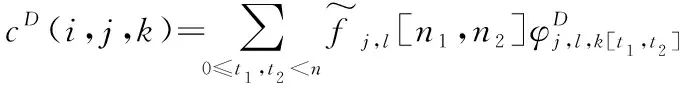
(4)

⑤取软硬阈值如下：

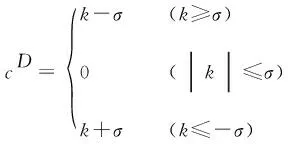
(5)

式中：是阈值。

1.2 压缩感知理论

压缩感知理论核心思想是如果信号是可压缩的或在某个变换域是稀疏的，用一个与变换基不相关的观测矩阵将高维信号投影到低维空间上，然后通过重构算法就可以从低维信号重构出原始高维信号(Candes，2005)。

假设气枪信号为()，其重构问题可以通过以下的模型进行表示：

()=[()]

(6)

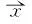
(7)

式中：是的等价或者稀疏表示。

根据缺失的位置设计一个平稳的、变换基不相关的×维的测量矩阵，这里选用一个服从(0,1)、正态分布、大小为×高斯随机矩阵来满足压缩感知理论对于随机投影矩阵的要求。对进行观测得到观测数据为：

(8)

式(8)为欠定方程组，有多个方程解，但具有稀疏性，可以通过不断促进的稀疏性进行反演求解。这就为实现缺失数据的精确重构成为可能。其中的稀疏促进策略(Herrmann，Hennenfent，2008)如下：

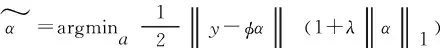
(9)

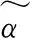
模型空间限制在x的一个L-ball 中。在(x,x)平面上可以画出目标函数直线,而约束条件则成为平面上大小不断变化的一个norm ball 。直线与 norm ball 首次相交的地方就是最优解。与L范数相比,L范数更有可能得到值为0的解(图1),使得x更具稀疏性(姚华建,2013)。

图1 L1范数(a)和L2范数(b)求解示意图(p表示范数)Fig.1 Schematic diagram of solving L1 norm(a) and L2 norm(b)

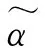
1.3 基于曲波域全变差的压缩感知降噪策略

气枪信号可以表征为()=+，其中，代表有效信号，表示为噪声信号。基于曲波域的阈值滤波方法(CSCT)，域中小系数容易被过度去除，缺失信号关键细节信息，并且不连续的区域常会出现震荡的伪影现象(唐刚，杨慧朱，2010)，影响数据的降噪资料。因此，需要首先利用压缩感知重建策略对因阈值滤波导致缺失的系数进行重建，解决信号稀疏特征的连续性问题，再通过全变差最小化技术对重建后的系数进行调整(Newark，1998；沈维燕，2006)，达到联合降噪的目的。

利用全变差最小技术对重建的曲波系数进行调整主要有两种方式：一种是调整大于设定阈值的系数：

+1=-(())

(10)

另一种是调整小于阈值设定的系数：

+1=-(())

(11)

式中：表示在小于设定阈值的曲波系数空间上的投影；表示在大于设定阈值的曲波系数空间上的投影；设置最大迭代次数和初始值，=1。()通过以下过程求解。

假设是中的有限子集，曲波域中系数的全变差定义为：

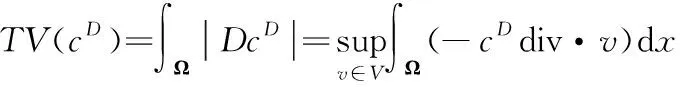
(12)

其中

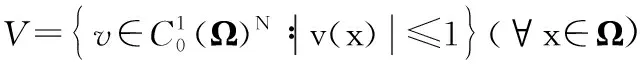
(13)

对上式进行分部积分得到系数函数的全变差为：

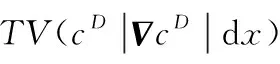
(14)

式中：为图像的支撑区间；∈为图像的坐标向量。

基于全变差的降噪方法可通过最小化()来实现：

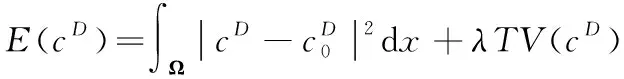
(15)

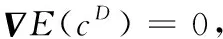
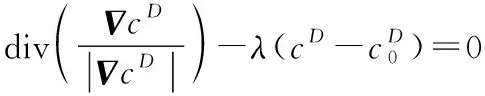
(16)

假设其满足Neumann边界条件，可通过投影梯度算法进行求解：

+1=-(())

(17)

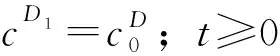
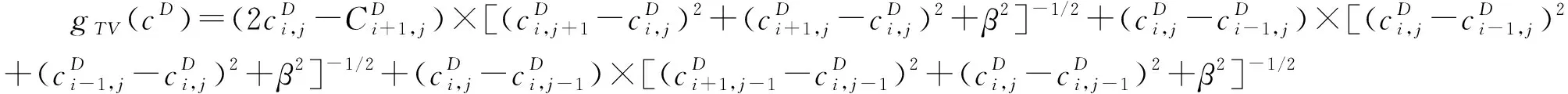
(18)

式中：>0为一个很小的正值，以解决全变差函数在某些点的不可微性，取步长

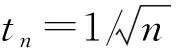
(19)

式中：=+1，判断是否接近，如果是迭代结束，否则继续求解次梯度。

基于曲波城的压缩感知降噪方法具体的流程如图2所示。

图2 基于曲波域的压缩感知降噪方法流程图Fig.2 The compress sensing denoising method based on curve wave domain

2 数值模拟

为了验证方法的有效性，利用信噪比值及均方根误差来衡量气枪信号的降噪效果：

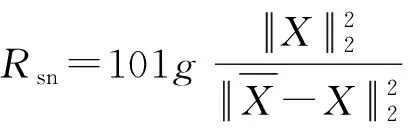
(20)

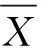
(21)

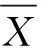
2.1 气枪信号数值模拟

基于曲波域全变差的压缩感知降噪方法对低信噪比的气枪信号实现了高效稳定的降噪效果。为了验证该方法应用于气枪信号降噪的处理效果，其中，已知的理论一维信号长度为1 400个采样点，信号带宽2～8 Hz，采样率100 Hz，且具有两个正弦周期(向涯等，2019)。在每道信号上随机加入6 dB高斯白噪声，再从100道中随机选择其中的9道按照线性递增的方式再次加入不同比例的随机噪声，噪声最高信号信噪比达到-15 dB，如图3a所示，从图中可以看出，加入噪声的9道信号相对原始信号已经基本看不出有效信号。

按照本文方法的处理流程，对加噪声信号进行降噪处理，在参数的选择过程中，其对曲波域阈值的选择综合对比了3种阈值(硬阈值、软阈值、软硬阈值结合)的降噪效果，其中软硬阈值结合的降噪效果较好，折衷系数选择0.001，能够最大限度保留信号的细节信息。在对曲波域系数进行压缩重建过程中，信号的缺失率不能低于30%，否则信号不能得到有效恢复。迭代次数选择也尤为重要，次数较大会引入随机噪声，较小对信号的细节信号恢复效果较差，综合尝试后认为选择迭代6次较为合适。处理结果如图3b所示，从图中可以看到，即使信噪比很低的信号，随机噪声都能得到很好地压制，与模拟信号的波形和振幅一致性仍较强，相位恢复精度较高，获得较好的处理效果。

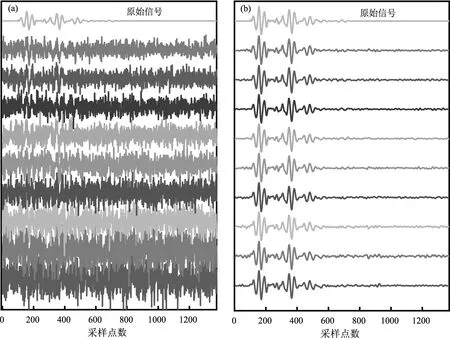
图3 模拟信号加载不同比例噪声(a)以及本文方法降噪结果(b)Fig.3 The original signal loaded with different proportions of noise(a)，and the noise reduction by the method in this paper(b)

为了进一步验证该方法的可行性和优势，本文引入带通滤波(BDF)、小波变换滤波(DWTF)、S变换模板滤波(STTF)，分别对加噪声信号进行处理，过程如下：用带通滤波对信号进行2～8 Hz带通滤波。小波变换滤波利用小波函数对信号进行小波3层分解后，其中阈值统一取1，进行阈值滤波。S变换模板滤波对信号进行叠加后，变换到时频域中，通过设定时频域区间的阈值窗口得到滤波模板，利用滤波模板再对信号进行滤波。4种方法的处理结果如图4所示，选择其中一道进行处理效果评价(图5)。

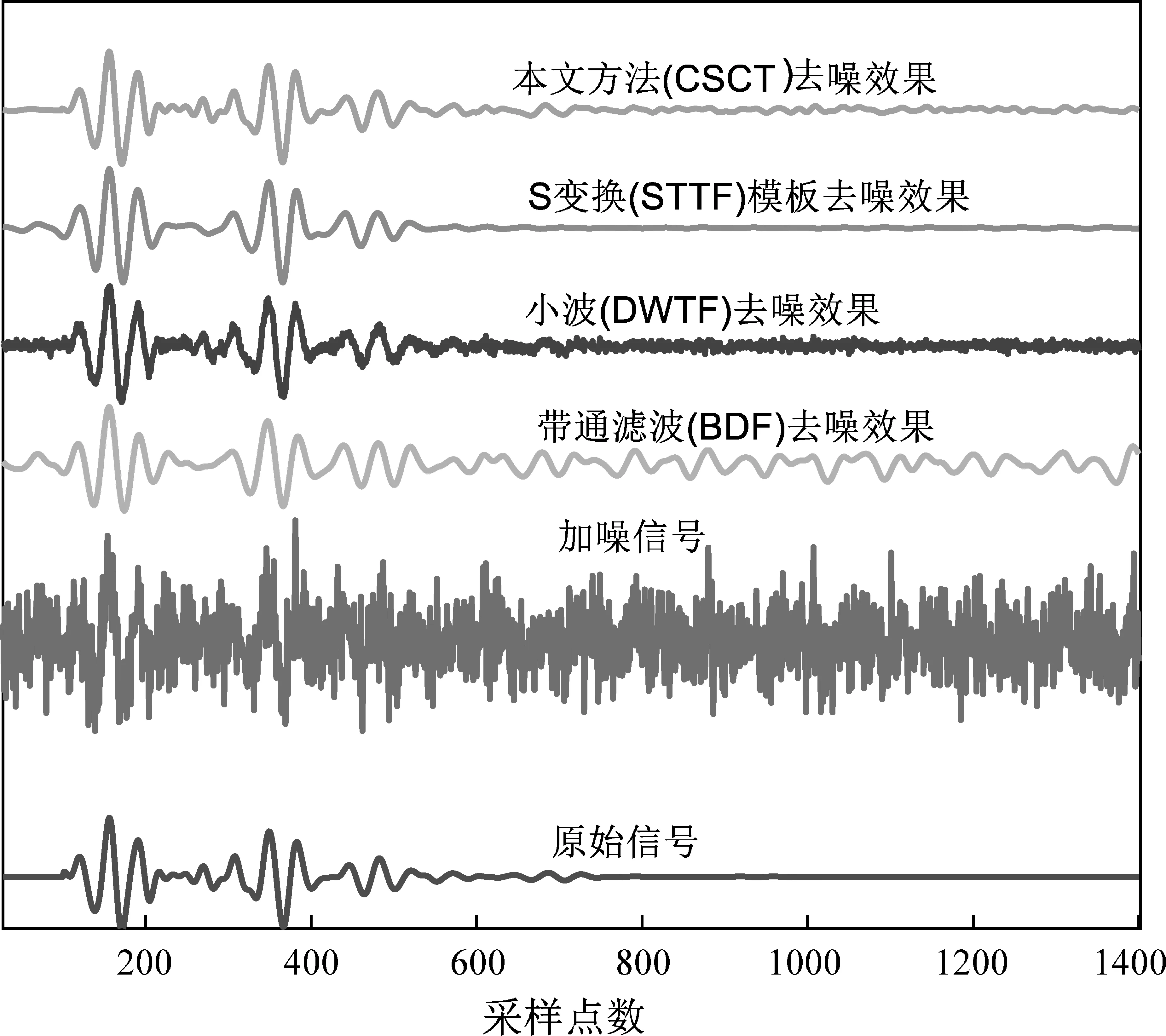
图4 不同滤波方法与本文方法处理效果对比Fig.4 Comparison of processing effects between various filtering methods and the method in this paper

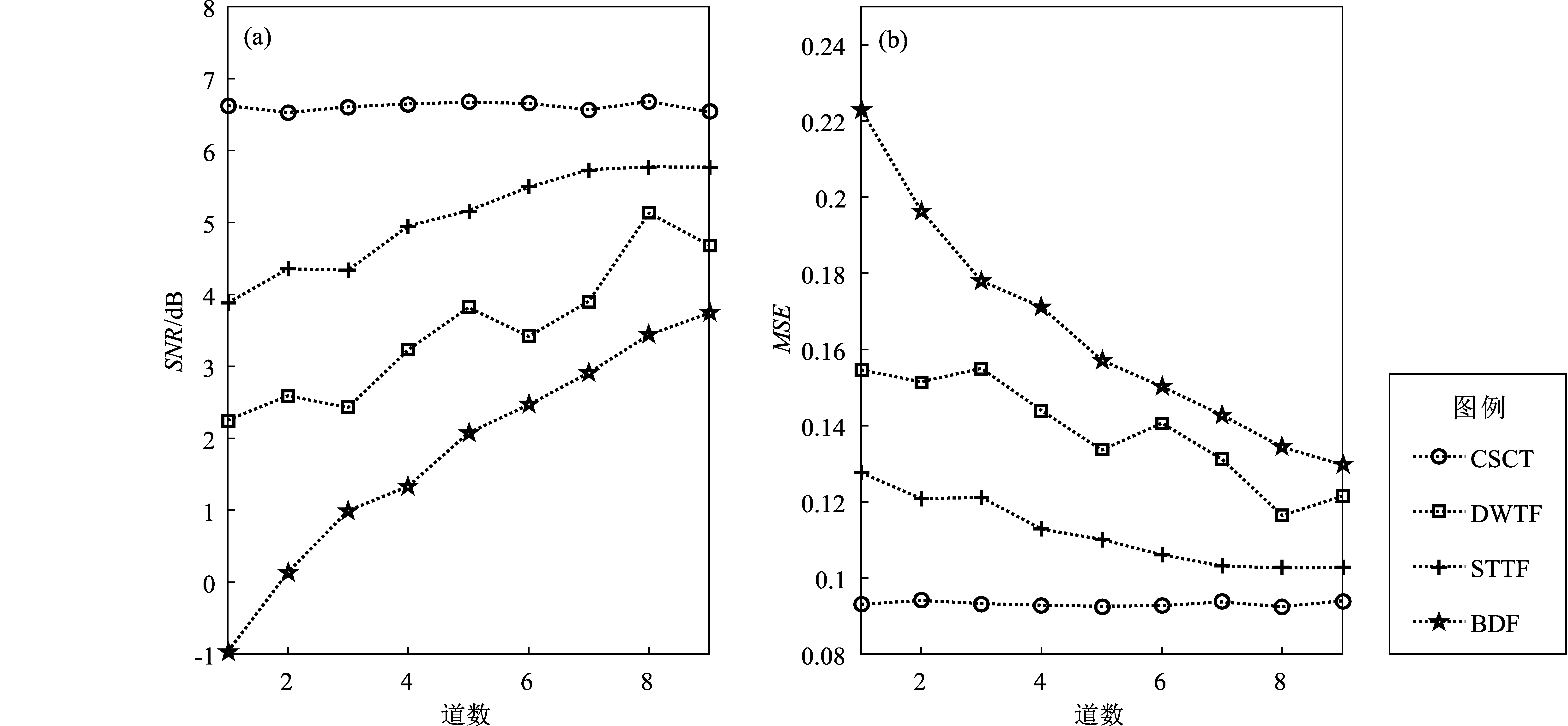
图5 不同滤波降噪方法处理结果的信噪比(a)和均方根误差对比(b)Fig.5 Comparison of the results of SNR(a)and MSE(b)by different filtering and noise reduction methods

如图5所示，通过对4种方法处理结果的信噪比和均方根误差可以看出，随着噪声比例越高，传统的几种方法处理后的信号越低，均方根误差越高。而本文的方法对不同比例的噪声信号降噪效果明显高于其它方法，即使信噪比很低也能达到很好的效果，并且稳定性更强。从单一道的处理效果(表1)来看，BDF方法可以将高频成分去除，但是与有效信号频率相近的噪声依然存在。用DWTF方法处理后虽然有效信号得到加强，但是高频成分随机噪声依然存在，STTF方法虽然克服了前两者的缺点，但是部分相位没有得到有效恢复，造成细节缺失，而本文的方法不仅很好地压制了随机噪声，而且恢复了对相位细节。

表1 不同滤波降噪方法的处理结果对比评价Tab.1 Comparison and evaluation of processing results of different filtering and noise reduction methods

2.2 波速测量精度评价

为了进一步验证本文方法在波速测量中的高效稳定性，由已知一维气枪信号利用移动窗口压缩-拉伸法(Meier，2010；刘志坤，2010)生成波速变化率不超过±5%的100道二维模拟信号(图6a)。在每道信号上随机加入6 dB高斯白噪声，再随机从100道中选择其中的9道按照线性递增的方式再次加入不同比例的随机噪声(同2.1节)，如图6b所示。按照上述的处理流程分别对加噪声信号进行降噪处理，对含噪信号进行2～8 Hz带通滤波。利用小波函数对信号进行小波3层分解后，阈值统一取2，进行小波阈值滤波。对信号所有道进行叠加后，变换到时频域中，通过设定时频域区间的阈值窗口，得到滤波模板，从而达到利用叠加信号进行模板滤波的目的。

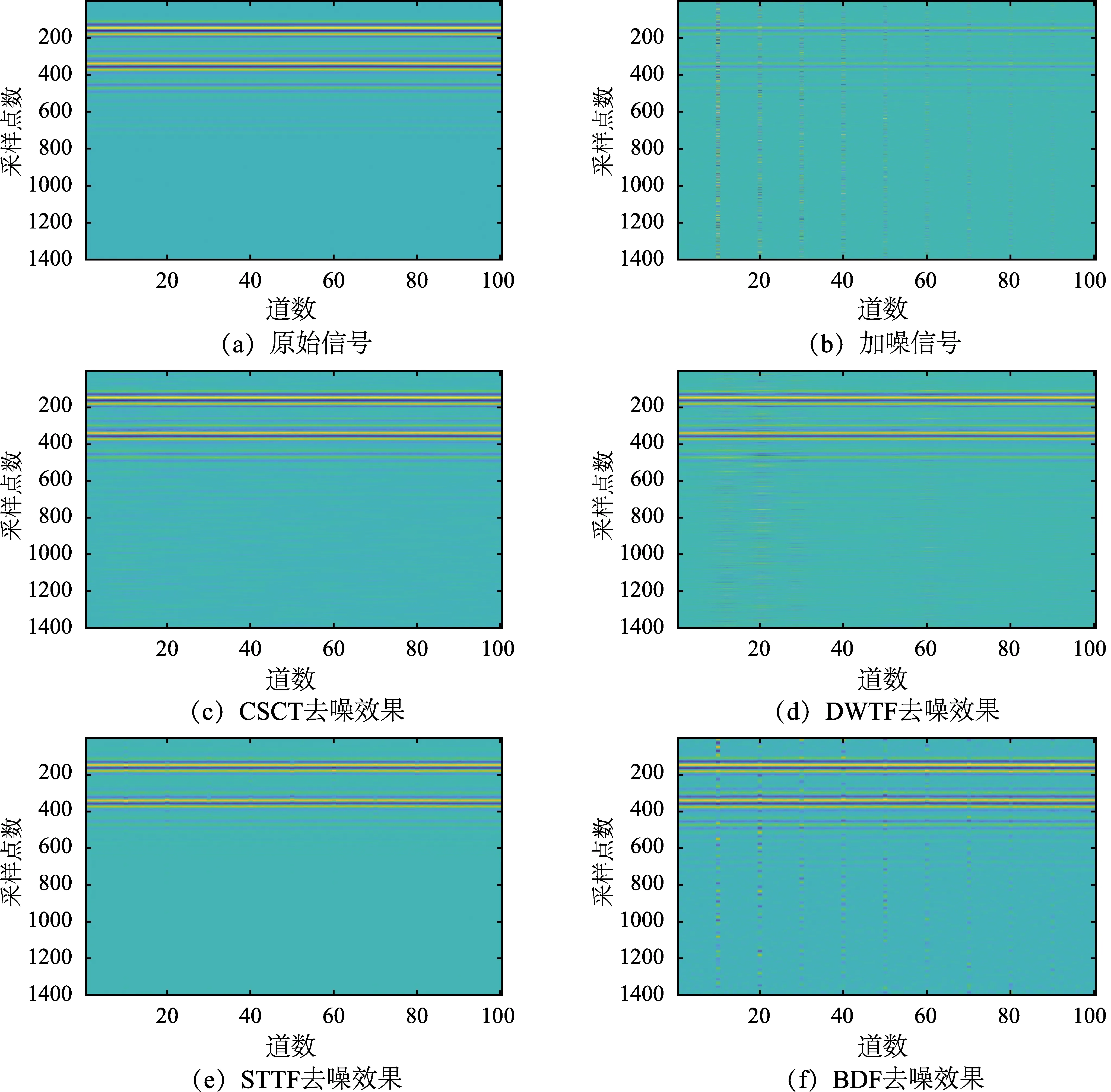
图6 使用不同滤波降噪方法对二维波速变化率的模拟信号处理后的降噪结果对比Fig.6 Comparison of noise reduction results of analog signals with two-dimensional wave velocity change rate by different filtering and noise reduction methods

由图6c可以看出，本文方法不仅可以很好地压制随机噪声，也去除了随机的线性干扰；DWTF虽然恢复了有效信号的大部分能量，但是对高频成分的噪声压制力较弱(图6d)；STTF方法对随机噪声的压制力较强，但是由于模板阈值的选取存在一定的误差，导致对信号细节的恢复较差，并且对加入的较强随机线性干扰的压制能力较弱，一些线性干扰依然存在(图6e)；BDF方法只能对固定频段的噪声进行压制，高频噪声和线性干扰依然存在(图6f)。

为进一步验证本文方法的稳定性和高效性，对上述几种降噪方法处理后的信号进行波速测量精度评价，如图7所示。

从图7可以看到，利用本文方法降噪后测量的信号波速变化率与模拟信号(蓝线)的量级一致，波速变化曲线基本一致，且拟合度较高。用DWTF方法处理后测量的信号波速变化率虽然与模拟信号的趋势一致，但是依然存在一定的误差，并且在较强的线性干扰处存在突变，用BDF方法处理后测量的信号波速变化率由于对随机噪声和线性干扰压制较弱，导致波速测量的精度严重不足，并且在较强的线性干扰处存在突变量。

图7 不同滤波降噪方法处理后波速测量结果Fig.7 Wave speed measurement results after processing by different filtering and noise reduction methods

3 实际气枪信号处理

云南宾川气枪主动源区域(25.4°～ 26.4°N，99.8°～101.2°E)位于由红河断裂、剑川—丽江断裂和程海断裂围成的三角形块体内，该区主体在大理—丽江活断层系(王彬等，2016)，是由正断和左旋走滑断裂构成的“Z”型张扭性复合变形带，包括丽江—大理断裂带和程海—宾川断裂带，一系列近SN向与NW向的断裂在此交汇叠加(张云鹏等，2020)。近年来，随着宾川主动源的建成，研究区内不仅建有40多个主动源流动地震观测台阵，还有多个固定地震观测台站，台站密度明显提高，并积累了大量地震观测资料，为开展相关科学研究提供了良好的数据保障和基础(Wang，2016；Jiang，2019)。但是震中距大于20 km台站的记录信号信噪比普遍较低(陈蒙，2014；向涯等，2017)。虽然可以利用气枪信号的高度重复性的特点通过信号叠加提高信号的信噪比，但是提高单次激发气枪信号的信噪比，不仅可以提高气枪激发信号的利用效率，而且对提高介质波速时空变化测量精度具有重要意义。

本文选取距离气枪发射源81 km的53251台站的信号，先对信号去均值、去趋势等处理，然后再利用本文的方法对信号进行降噪处理。实际气枪数据采样率为 100 Hz，由于距离较远，随机噪声干扰较多，尤其是信号受到很多线性干扰的影响，使得数据信噪比较低(图8a)。本文利用不同滤波方法对实际气枪信号进行降噪(图8b～e)。

从图8b可以看出BDF方法只能对固定频段的噪声进行压制，高频噪声和线性干扰依然存在。

图8 不同滤波降噪方法对实际气枪信号的处理效果对比Fig.8 Comparison of processing effects of different filtering and noise reduction methods on airgun source singnals

DWTF方法虽然恢复了有效信号的大部分能量，但是线性干扰依然存在，对高频成分的噪声压制力较弱(图8c)。STTF方法对随机噪声的压制力较强，但是由于模板阈值选取的不稳定，部分有效信号能量没有恢复，并且对加入的较强随机线性干扰的压制能力较弱，一些线性干扰依然存在(图8d)。本文滤波方法不仅可以很好的压制随机噪声，也很好地去除了随机的线性干扰，对同相轴的连续性和一致性恢复较好(图8e)。

为了更加清晰地对比多种方法降噪效果，本文对上述实际气枪信号进行1 500次叠加，并进行2～7 Hz带通滤波，选择其中一道气枪信号进行对比分析，并将处理后的信号与叠加信号进行互相关分析，结果如图9所示。

图9 不同滤波降噪方法处理结果与叠加信号对比评价Fig.9 Comparison and evaluation of processing results of different filtering noise rodution methods and superimposed signals

由图9可见，经BDF方法处理后高频成分被去除，但是与有效信号频率相近的噪声依然存在，互相关系数仅为0.880 7。经DWTF方法处理后虽然有效信号得到加强，恢复了信号的大部分能量，但是高频成分随机噪声依然存在，互相关系数为0.888 2，STTF方法虽然克服了前两者的缺点，互相关系数达到0.941 7，但是部分相位没有得到有效恢复，造成细节缺失。而本文的滤波方法处理后互相关系数达到0.986 0，不仅很好地压制了随机噪声，而且恢复了相位细节，取得了较好的降噪效果。