始于“活动”，成于“转化”，促深度学习

吴建惠　周敏刚　李硕

[摘  要] 随着深度学习走向数学核心素养实践教学落实的逐步深入，这种新型的教学理念与实践探究方式也在促进课堂教学的改革.在初中数学课堂教学中，深度挖掘教材意图、依托数学活动载体、创新设计数学活动、挖掘活动潜在价值，提高学生参与活动的积极性，使学生在活动中经历与感悟，在实践中思辨与质疑，在本质上抽象与转化，在结构上建构与联系，使深度学习在课堂真正发生，促进初中学生数学核心素养的养成.

[关键词] 数学核心素养;深度学习;数学活动

深度学习是课程改革以来对课程理解和课堂实践的深化，它既是一种理念，也是一种实践指导策略[1]. 在新一轮的教学改革中，深度学习走向数学核心素养培养，从理论完善逐步到落地指导教学实践，因此对于深度学习的研究有必要回到课堂教学中去[2].

初中学生对数学知识的理解，在于经历发现的过程、理解知识本质、体会思想方法、促进数学核心素养发展. 在数学学习中，数学知识的学习是实现数学思维的发展、各种问题的解决、思想方法的感受、数学价值的体会的基础[3]. 数学学习过程是教师、学生围绕学习内容而展开的活动过程，初中深度学习要求学生能够全身心投入具有挑战性的、富有思维含量的数学活动[1]. 让初中学生参与富有思维含量的数学活动，这就需要教师能够对教学活动进行高效转化. 笔者作为指导教师参与了“最短路径问题”的备课、磨课，引发诸多思考，现就创新教学活动设计、抽象转化解决问题、促进学生深度学习等方面的一些做法与大家分享.

“兵马未动粮草先行”的思考

一个好的问题情境必须基于学生的已有经验、学习内容和学习环境进行综合考虑，充分激发学生的好奇心和求知欲，引发学生的深层兴趣，促进学生携带自己对学习内容的已有理解卷入学习活动中来[2] . 针对学生的学习情况，教师反复磨课，结合教学经验提出以下思考问题.

思考1：本节课是“课题学习”课，与其他的课有什么不同？

思考2：本节课作为“轴对称”的章节最后一课，应发挥怎样的教学价值？

思考3：“最短路径问题”多与近几年新疆中考压轴题整合出现，解决此类问题对学生的要求很高，通过本节课学习，要重点培养学生哪些关键能力？促进学生哪些数学核心素养的发展？

思考4：怎样将这些能力培养点恰当地融入教学活动中？

带着这些问题反复交流思考. 我们认为：从课的类型上看，“课题学习”在人教版教材中占比极少，一部分教师会把“课题学习”课当作习题课来上，使学生错失了参与数学活动与实践的机会. 参与磨课的交流者一致认为“课题学习”既不同于新授课，也不同于实践课，它应该是以知識应用为起点、学生参与为方式、问题解决为目标的综合课;从教材的整体性上看，作为本单元的结课内容，在知识上是对本章的概括与综合应用，在结构上还应从“图形与几何”的单元教学的视角思考本节课安排两个活动的内在关联;从内容的综合性上看，“最短路径问题”多与几何图形、函数问题融合在一起，考查学生综合解决问题的能力，基于这种高度的综合性，教师要以数学活动为载体，有机地融入真实情景中，凸显数学转化的能力，逐步引导学生形成对以往知识经验的调取的思维方式.

“知所不豫，行且通焉”的实践

（一）以《古从军行》诗词引入，渗透中华传统文化

师：我国唐代诗人李颀的《古从军行》“白日登山望烽火，黄昏饮马傍交河”诗句中描绘了将军饮马的场景.

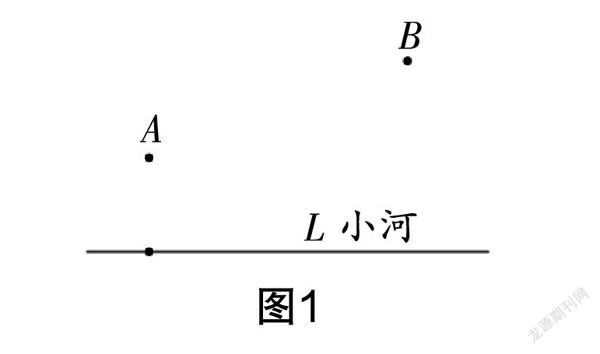
问题1：如图1，牧马人从A地出发，到一条笔直的河边L饮马，然后到B地，牧马人到河边的什么地方饮马，可使所走的路径最短？

教学说明：问题情境不仅将学生引入活动的情境之中，激发了学生学习的兴趣，还将中华传统文化融入其中，在趣味中蕴藏着数学问题，以问题为导向，引发学生的思考.

（二）深挖数学活动內涵，以“联系”促“转化”

对于“将军饮马”这个经典问题，在平常教学中，往往是“探而不究”“浅尝辄止”，做对称点的想法和做法一般是教师告知给学生的，教师只是教会学生“怎么做”. 在这样的学习过程中，学生处于被动接受和简单模仿的状态，显然学生的理解是浅显的，思维是低阶的. 相对于此，采用深度学习的学生将采用更高水平的认知加工方式[2]. 对于这个问题的处理，执教者对“为什么这样做”“怎样想到这样做”进行了思考，做了如下创新设计.

创新点1：借助学生画图与演示帮助学生理解将同侧点转化为异侧点的必要性和可行性.

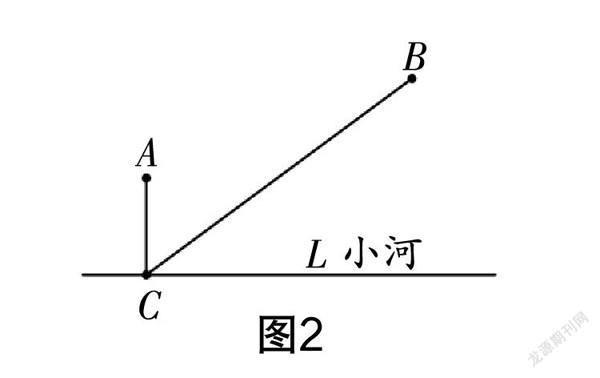
先让学生自己画图探寻动点C的位置，教师巡视学生所画图形，发现有相当一部分学生是过A点或B点向直线L作垂线段（如图2），此时教师追问：“确定此时AC+BC最短吗？”在教师的追问下，一部分学生开始转换思路，运用刻度尺测量验证，发现当C点在垂足处时AC+BC并不是最短的. 这种认知上的冲突极大激发了学生深入探究的欲望，但由于C点是一动点，位置难以确定，学生的思维受阻. 此时教师利用几何画板演示，并利用几何画板的度量功能显示AC、BC及AC+BC的值，拖动C点，当C点从左往右运动时，AC+BC的值越来越小;经过某一时刻，继续拖动C点从左往右运动时，却发现AC+BC的值反而越来越大. 由此可以断定：1.最小值是存在的. 2.满足条件的C点应该在两个垂足之间.

如何确定C的位置？教师通过引导学生与自我对话，与其他同学交流，启发学生产生联想，到目前为止，学生思维的最近发展区有两个，分别是“垂线段最短”和“两点之间线段最短”，当排除了“垂线段最短”的思路后，自然会联想到“两点之间线段最短”. 但此时两定点在定直线的同侧，为了在直线上产生动点，教师应引导学生将直线同侧点通过点的映射转化到异侧，利用“两点之间线段最短”成功将动点位置锁定.

教学说明：上述活动设计，学生积极参与到探究问题中去，经历了“画图抽象→认知冲突→思维矫正→测量再探→引导转化→化动为定→问题解决”的学习过程，形成了将军“饮马问题”的数学模型. 基于以上的深入探究，学生对问题的感受是深刻的，对问题的理解也是深刻的，将外显于形的活动逐步内化于心.DB8C42CB-EB13-4F29-8E56-BCEFD14046BF

创新点2：通过学生动手操作将“架桥问题”转化为“饮马问题”模型.

对于知识的应用于迁移，可以通过变式练习的方式实现. 教师将课本中的问题2改编为：如果将河岸改为一条河，牧马人从河一岸的A点去河另一岸的B点，现要在河上架一座小桥PQ，桥造在何处可使从A到B的路径APQB最短（假定河的两岸是平行的直线，桥要与河垂直）？

这个问题极大地激发了学生的兴趣，问题被抽象成求AP+PQ+BQ的值最小问题（可以看作是两定两动模型），学生跃跃欲试后发现无从下手，此时教师设计以下活动.

学生活动：请在作业纸上试着画一画，找出架桥的点，完成作图并证明. 作图前可先思考以下问题，有了一定想法后可在小组内交流：

（1）需要找某个点的对称点吗？

（2）求AP+PQ+BQ的值最小问题可以通过转化而简化吗？

（3）能不能将此问题与将军“饮马问题”联系起来？

学生的做法大大超出教师的预期，下面展示一个小组学生的对话.

生1：不用找对称点，直接连接AB.

生2：你的做法不对，直接连接AB的话，桥PQ就与河岸不垂直了.

生3：既然河的宽度是固定的，AP+PQ+BQ的值最小问题可以先转化为求AP+BQ最小，那我们是不是先把河宽看作是0.

生2：怎么可能？

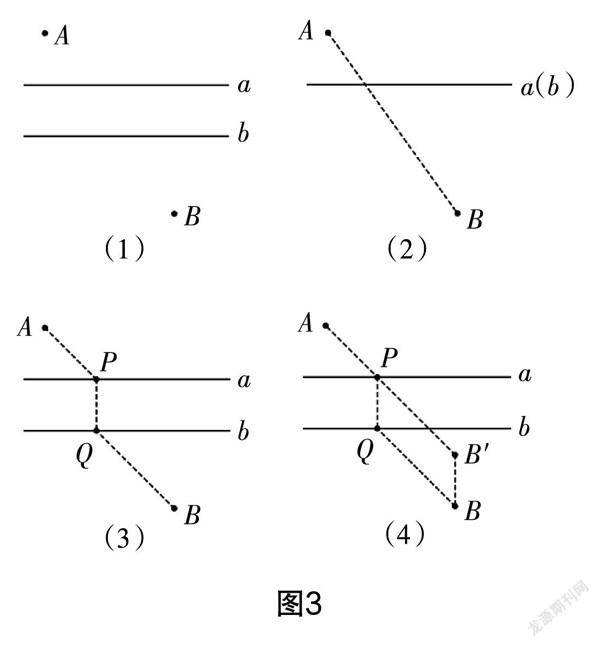
生3：在练习纸上画好图（1），先将纸沿直线b折一折，再将直线b向上平移，直到与直线a重合，点B就随着纸张被平移了一个桥长，落到了点B′的位置，此时问题就转化成图（2），即将问题转化成了“将军饮马”模型，连接AB′，交直线a于P点，然后再将纸展开，直线b还原到原来的位置，此时，过P点向直线b做垂线段，垂足为Q，连接QB，如图（3）所示，AP+BQ即为最短，最后连接B′B，获得PQBB′是平行四边形，成功将QB转化为PB′的长，利用两点之间线段最短获证.

教学说明：学生在已有知识储备的基础上产生联想，经历不断试错、不断调整思路的过程，通过将有河宽的问题进行平移转化为“饮马问题”基本模型. 解决问题的思路是学生亲身实践获得，由定点B→沿着与河岸垂直方向平移一个河宽→得到B′→连接AB′→确定动点P的位置→沿着与河岸垂直的反方向平移一个河宽→确定动点Q的位置. 学生在直观操作中加深了对问题的理解，对接下来的推理证明也能够顺利实施.

实践后的反思

（一）以“问题”为导向促进教师深度思考

问题是数学的心脏，也是撬动教师思考的杠杆. 通过对平常所谓“熟悉”的教学进行再挖掘，从教材的整体视角、从学生的学习视角、从素养的培养视角提出问题，靶向问题，以问题为导向促进教师深度思考，使教师在向“理解数学、理解教学、理解学生”的路途上又迈进了一步. 以问题为导向既立足教材又高于教材，既凸显数学学科本质又体现学科育人价值，从行动上诠释了“用教材教”的理念，教学立意从知识立意向能力立意与素养立意转变.

（二）以“活动”为载体促进学生深度参与

《义务教育数学课程标准（2011年版）》中提到：数学教学应根据具体的教学内容，注意使学生在获得间接经验的同时也能够有机会获得直接经验[4]. 通过创设具有问题情境的活动，为学生搭建实践、思考、探索、交流的平台，不断引发质疑与思辨、调整和纠偏，尝试与创新，在掌握基础知识、基本技能和基本思想的基础上积累基本活动经验. 数学活动不仅要关注教师的深度教学，也要关注学生思维的成长. 本节课以两个活动为载体，使学生经历了画图、测量、折纸、猜想、推理的过程，在活动中思考、在活动中感悟，在活動中提升了学生发现问题、提出问题、分析问题、解决问题的能力，促进了深度学习在活动中的落实.

（三）以“转化”为突破促进思维深度发展

数学教学问题“遇难则转”，教师要以问题转化为突破口，将未知的、有困难的问题通过转化这一桥梁实现由繁到简、由未知到已知的过渡，实现在学生知识与思维的最近发展区嫁接新的知识方法的目标，让知识与能力自然生长. 在探究“架桥问题”时，学生很容易借鉴“饮马问题”的活动经验，联想到利用“饮马问题”模型来解决，但两个问题又有不同，架桥问题是双线问题，“饮马问题”是单线问题，认知出现了冲突怎么办？靠转化.

于漪说：“现在的老师不缺教学技巧，而缺思想与批判性思维. ”学生在对连接AB的做法进行否定后，似乎进入绝境，执教者巧妙利用学生的生成资源，将“桥的宽度不影响最短距离”引导为“将桥宽暂时看作为0”，通过平移一条平行线成功将问题转化为“饮马问题”模型，由双线双动点（架桥问题）转化为单线单动点（饮马问题），在纸张折叠过程中，学生直观可见随着直线b的平移，B点也平移了一个河宽，不仅解决了“怎样做”的问题，还解决了“为什么这样做”的问题. 学生的思维经历了简单模仿、思辨质疑、猜想论证的过程，对问题有了既直观又深刻的理解，发展了几何直观、数学抽象、逻辑推理的学科素养，此时的课堂因转化而精彩，思维因抽象而进阶.

（四）以“联系”为观点促进知识整体建构

《义务教育数学课程标准（2011年版）》中强调：要把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识和整体知识的关系，引导学生感受数学的整体性. 数学家G.波利亚说过：好问题如同蘑菇，它们都成堆的生长，找到一个以后你应当再去周围找一找，很可能附近就有好几个[5]. “饮马问题”“架桥问题”并不是两个孤立的问题，在它周围我们可以发现其他的“蘑菇”. 站在初中“图形与几何”的单元教学视角来看，解决线段和最小问题的基本思路是抓住不变特征剥离基本图形，确定定点和定线，利用轴对称、平移、旋转等图形变换，将不共线的线段转化为共线的线段，实现“折转直”，再依据“两点之间线段最短”获得线段和最小的结论（如图4）. 这样既关注了知识的生长点又重视了知识的延伸点，形成了研究问题的整体和转化思想，帮助学生建构知识框架，便于学生整体理解章节知识，有利于学生深入思考，更有利于问题的分析与解决，做到既见树木，又见森林.

结束语

深度学习是一种基于高阶思维发展的理解性学习，具有注重批判理解、强调内容整合、促进知识建构、着意迁移运用等特征[6]. 深度学习在大单元教学理念的设计下，始于“活动”，成于“转化”，从而不断推动教学理念与教学实践的发展. 深度学习是核心素养导向下的课程教学改革的需要，是一线教师不断深化理论基础与推进实践教学的探索，是教师教学思想、理念、能力的集中体现. 有了教师对深度学习的深入理解与应用，才会有课堂上学生的批判理解、联系建构、转化迁移、灵活运用，深度学习才会真正发生，学生数学核心素养才会逐步养成.

参考文献：

[1]刘晓玫，黄延林，顿继安，等. 深度学习：走向核心素养（学科教学指南·初中数学）[M]. 北京：教育科学出版社，2019.

[2]张春莉，王艳芝. 深度学习视域下的课堂教学过程研究[J]. 课程·教材·教法，2021，41（08）：63-69.

[3]刘晓玫. 数学深度学习的教学理解与策略[J]. 基础教育课程，2019（08）：33-38.

[4]中华人民共和国教育部. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[5]徐军. 寻找周围的“蘑菇”[J]. 高中数学教与学，2005（02）：6-8.

[6]安富海. 促进深度学习的课堂教学策略研究[J]. 课程·教材·教法，2014，34（11）：57-62.

基金项目：新疆维吾尔自治区一流本科专业——昌吉学院“数学与应用数学”（新教函[2020]61号）;新疆生产建设兵团第六师教学研究和师资培训中心课题——初中数学课堂教学“引·探·导·测”教学模式研究（LSKTJX2019056）;“自治区普通高校人文社会科学重点研究基地（培育）——昌吉学院新疆基础教育质量提升研究中心”.

作者简介：吴建惠（1970—），昌吉市教育局教研员，高级教师，大学本科，昌吉学院硕士生导师，从事数学教育研究.

通讯作者：李硕（1975—），昌吉学院数学与数据科学学院教授，硕士生导师，从事课程与教学论、运筹学及算法、数学模型等研究.DB8C42CB-EB13-4F29-8E56-BCEFD14046BF