完善视觉体验，升华直观认知

2022-06-22江苏南京市金陵小学210033

小学教学参考 2022年11期

江苏南京市金陵小学（210033）涵楚

数学学习中的观察不是漫不经心的赏玩，而是带着专业的数学思考，通过数学的眼光来看待事物和现象，做出数学性的分析，并在此基础上对所思所想、所感所悟进行归纳总结，形成抽象的、稳定的概念，并存储在个人知识库之中。然而，许多时候，学生看问题时只是浮光掠影，或者一叶障目，不见泰山；或者盲人摸象，只知其一……针对这些现象，教师不应偏执地指责学生“不用心，不用功”，而应该从视觉感官刺激受阻的角度出发，变换方式来呈现学习材料或者换种方式来传递视觉信息，设法刺激学生的视觉信息转化神经通道，不遗余力地提高学生数学观察活动的效果。

一、增强观察动机

真正的观察活动，多是从观察对象的外在结构获得初步感知和大体印象的，如从外部形态结构和各部分的架构关系来发现规律，或者发现一些有趣的地方、不可思议的地方。总之，通过初步观察发现一些不同寻常之处，可以牢牢吸引学生，使学生的注意力集中在被观察对象的显著特征上。

如在“7 的乘法口诀”的巩固练习环节，教师创设了“比较一下谁的眼尖”的趣味竞赛游戏。PPT出示“蜡笔小新吹肥皂泡”的情境图（如图1），肥皂泡上随机显示有关7 的乘法口诀中的任意的6 句。游戏任务就是找出到底少了哪句口诀，谁耗时最短谁就获胜，以此考验学生的瞬时观察能力。学生屏息凝神，专心致志，目不转睛，默念口诀，逐一核查。每次查找到目标，学生都欢呼雀跃。随后，PPT 又切换成与7 的乘法口诀有关的6 个积，让学生找出缺少哪个积。游戏重复了4 次，学生仍然恋恋不舍。将死记硬背口诀“乔装打扮”为妙趣横生的“寻宝游戏”，无须教师在一旁反复监督和强调，也无须教师时刻提防学生走神，别开生面的游戏设计让学生兴致勃勃、心无旁骛。

图1

又如，教学“找规律”一课时，教师特意组织了一场记忆比赛：在3 秒钟内速记长串数字，男生分到的数是“162536496481”，女生分到的数是“123412341234”。比赛结果是男生组输。他们不服气，提出他们分到的数要比女生的难记，不公平。这充分表明他们对两组数据进行了仔细比对。的确，女生的数具有规律性。但教师指出男生的数也有规律，引导男生再次仔细观察自己组的数据。男生看了半天，终于参透里面的奥秘：“162536496481”的规律是“16，25，36，49，64，81”——几个连续自然数的平方数。

在上述两个教学片段中，数学知识游戏吸引了学生，他们感到新鲜好玩，产生一种探秘的强烈冲动。在游戏通关欲望的驱使下，学生努力思考数学问题的破解之道，从而鞭策自己认真观察，积极投入到愉悦兴奋的视觉体验中。必须指出的是，单单是形式上的新颖，只能短时间内吸引学生。因此，教师既要设法将学生的游戏玩乐动机转化为学习求知动机，也要设法将学生的玩耍趣味推向带有数学理性思考的深度，给学生的视觉体验贴上“数学思考”的标签。

观察活动是最基础的数学实验活动，但观察活动也是要有动机的，过去的动机就是教师的命令。教师先出示观察材料，然后让学生按照要求一步步来观察，先观察什么再观察什么，观察后思考什么，或者对比观察，看看有什么不同，要归纳出什么性质特征。不过，这些都不属于真正的动机，因为这些带有目的性的观察或者说以问题为导向的观察都是“应景之作”，是学生在附和教师，学生思维的有效性和活跃度是十分有限的。自发的观察才是来自学生的内在需求。虽然一开始是没有目的的观察，但随着观察的深入，学生自然会寻找到观察目标，从而进行有目的地观察。这个目标是自定的，是学生根据自身的兴趣和内需自我构建的，所以后期的观察自然会忠实地服务于这个目标，这是学生自我解答、自我实现的通途。

二、过滤非主要视觉元素

所谓的观察，不仅是用眼看，更要用心感受。科学的观察分为粗略印象和带有数学分析的检视两个步骤，每一步都不可或缺，每一步都有着各自重要的功能。为了确保学生能够积淀有益的数学观察经验，必须科学规范学生的观察行为。

例如，教学“折线统计图”时，学生在观察对比条形统计图和折线统计图后，能通过整体感知察觉“折线统计图不但能表示数量的多少，而且能反映数量增减变化的情况”，但是对这两种统计图的特性却不甚了解，尤其是不知如何根据数据特点选择统计图。为此，教师首先出示苏州月平均气温条形统计图，让学生在仔细观察统计图后说说图中给出的信息，并追问：“还能看到什么呢？”引导学生找出条形统计图无法直观揭示的信息，如研究两个月之间的温差，以及连续几个月的气温变化时，条形统计图明显存在不足，而折线统计图正好可以弥补这些缺陷。接着，教师用PPT演示条形统计图逐渐演变为折线统计图的动画，让学生观察对比这两种统计图。最后，将统计图拟人化，让学生领悟条形统计图上的每个月都是一个独立的“管家”，12 个月就是12 个“管家”，互不相干、各自为政，而折线统计图则恰恰相反，12个月只有一个“管家”。

屏蔽其他次要信息，聚焦“管家”的“职责范围”，让学生明白选择统计图的依据——看看有几个“管家”。这样的拟人化处理，不仅深刻揭示了两种统计图的不同点，突出了折线统计图的重要价值，而且为教学“条形”的“分散”和“折线”的“延绵”做好铺垫。

此外，在观察主题图时，如果不规范观察的路径，过滤掉非本质的信息，那么散乱庞杂的信息就会扰乱学生思维，让学生无所适从。因此，出示主题图后，教师可以提示学生缩小观察范围，锁定观察目标，最后根据学生的反馈，甄别、筛选、优化，选择一些典型让学生作专题研究。

“一千个读者眼里就有一千个哈姆雷特”，数学观察也是见仁见智的，不同的人由于生活经验和认知习惯不同，即使观察同样的素材，得出的数学结论也会不一样。这就需要教师引导学生按照数学的方法来观察，如观察条形统计图，就要专注于其通过高度反映各个数据的大小，很直观，而且各个数据之间严格分离，毫无联系。但是如果转换成折线统计图，那么观察的角度就要发生相应的变化。折线统计图淡化了各数据的高低，且将各数据之间的割裂和孤立状态转变为连续变化状态，反映的是同一个研究对象在不同阶段的数据变化，重在变化，不在具体某个点的大小，重在整体效应，不在局部效应。学生很难自主切换观察视角，而教师用“管家”来打比方，形象贴切，能引导学生正确地进行对比观察，进而帮助学生调整观察角度。只要角度对了，就能看准数学性质。

三、关注观察经过，理解原理

学生在观察中提取的感性认识，都是与实物、图形、操作经过等捆绑在一起的具体视觉信息，教师应对其进行必要的抽象概括。例如，在“长方体的认识”教学中归纳棱的特征时，教师就要引导学生对观察到的信息进行抽象，多次开展想象活动、推理活动，使直观印象转化成抽象概念。观察的角度、视觉成像的途径越多，积累的表象就越丰富，抽象起来也就更容易，理解起来也更省事。

而在研究“面”的特点时，教师则反其道而行，不再先观察后思考，而是先思考后观察。首先利用课件呈现一个长方体的长、宽、高（如图2），接着出示6 个平面（9×9，9×7，9×4，6×6，6×4，4×4），要求学生给长方体装配侧面。学生观察的是棱，感受的是棱的特性，教师布置的任务却是装配侧面。因为有前面观察活动的经验，学生很有条理地给长方体装配上前、后、左、右四个面。值得一提的是，提供的六个面中，独独缺少上、下两个面，需要学生去对比甄别，通过想象构图，并逐一对照检验，进一步发展了学生的空间观念。

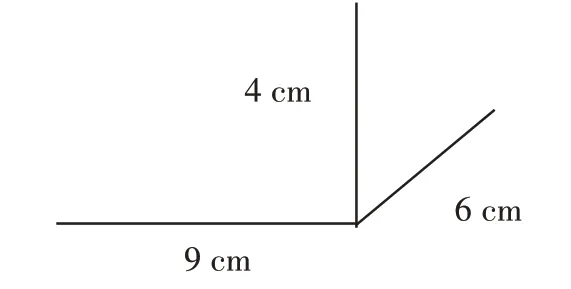
图2

所谓视觉信息，就是看到的物象或者图像经过提取、挑选、分析后形成的神经信号，不只是直接的投映，还包括对信息的加工、假设、改造、推理与创新。因此，贴切的教学情境，更便于学生从繁杂的视觉信息中抽象出事物的本质属性。

要提高观察活动的效果，不仅要对观察者进行引导，还要对观察素材进行精心设计和编排。观察素材如果太直接，看到什么就是什么，不但容易限制思维的发散，而且也容易使原本蕴含着丰富数学思想的观察变得干瘪苍白。如果能让观察对象和观察目标有一定的间隔，刚好能让学生发挥联想，将前后知识一一联系起来是最好不过的了。如教师让学生观察的是3 条棱，却让学生用6 个面来复原长方体的原貌，这促使学生不断回想、构建长方体的棱长与侧面的几何关系：长乘宽为上下面，长乘高为前后面，宽乘高为左右面。在这种“隔空”观察中，学生必须通过想象完成对长方体的修复。

四、完善观察结果的表达

课堂上，教师需要组织学生交流观察到的现象，并及时概括并做出范式表达，使已获得的知识理论化和学科化。以“倍的认识”教学为例，教师先呈现2 只野鸭和6 只鸵鸟的图片，让学生将每2 只野鸭和每3 只鸵鸟圈一圈，然后形成直观的倍数印象：野鸭有2 只，鸵鸟有3 个2 只，此时表示在数量上鸵鸟是野鸭的3 倍。然后，呈现野鸭2 只、鸵鸟12 只，教师提问：“此时，鸵鸟的只数是野鸭的多少倍呢？”

在学生展示汇报之后，教师提问：“观察时，你是怎么断定3倍和6倍的？”学生由“几个几”直观抽象出“倍”的概念：能圈出等量的几份就是几倍。然而，这样的视觉注意是被动强制实施的，并不是学生自发的。

因此，接下来有必要通过比较深化学生对“倍”的认识，挖掘“倍”的深刻内涵。教师先呈现一组都表示“鸵鸟的只数是野鸭的2倍”的图（如图3）。图的内容错综复杂，学生需要筛选出有用的信息——关于“2 倍”的基本特征，再寻找共性，准确表达。然后，教师出示图4 并提问：“你觉得哪幅图对应‘鸵鸟的只数是野鸭的几倍’呢？鸵鸟的只数是野鸭的3倍、还是2倍呢？”