学生计算易错题的分析及其应对策略

山东滨州实验学校（256600） 杨瑞芳

在数学计算中，各种错误在所难免。各式各样的错误背后蕴含着各种各样的因素，这些因素或反映学生的思维方式，或暴露学生的技能短板，或揭露学生运算中的逻辑漏洞，只要顺藤摸瓜，找准这些因素，就能帮助学生建立健全的运算机制，让学生养成自我检查、自我更正的习惯。

一、认真分析，甄别错误

对四年级某班学生在计算中所犯的错误进行调研，调研测试中编设了6 道计算题，单独看难度不大，运算量适中，但综合性较强。统计数据表明，学生的错误部分源于非关键因素的干扰。

【案例1】

①125×8÷125×8=1000÷1000=1

②13.72-1.8+8.2=13.72-（1.8+8.2）=3.72

③15-15÷3=0÷3=0

④3428-428×8=3000×8=24000

⑤10×10+24×5=100+100=200

⑥38×（825+75）=38×825+38×75

第①题：“125×8=1000”这种常见的固定搭配成了强大的诱导性信息，“凑整”习惯驱使学生产生强烈的凑整冲动，一见到这两个数字相乘就不假思索地去凑整，从而自动忽略运算顺序、计算法则等其他规则进行所谓的“简算”。学生直接落入经验陷阱。

第②题：依序计算较为棘手，学生产生畏难情绪。此时，凑整思想乘虚而入，使得学生只顾寻找符合凑整特征的数对，全然不顾计算法则，看到后两个数能够凑整，使自以为是地将后两个数合并起来。题中的“1.8+8.2=10”就属于强信息干扰，有着强烈的心理暗示作用。

第③题：观察算式时，学生一看到“15-15”的形式，就会想到直接相减得0，而“0”在四则运算中有着特殊的地位，凡是与之运算必然可以简化。这种想走捷径的心理，导致学生枉顾运算顺序，按照个人的主观臆想去计算。只顾结果不顾事实，错误在所难免。

第④题：3428 与428 都是较大的数，且尾数相同，正是这种显著的特征“引诱”学生将这两个数进行相减。因为一旦相减，“整千数”就唾手可得，后面的计算就会变得简单。

第⑤题：“25×4=100”是凑整乘数中的经典搭配，学生极易形成刻板印象，而“24×5”与“25×4”非常形似，学生常常张冠李戴。

第⑥题：受乘法分配律“a×（b+c）=ab+ac”形式上的影响以及长期以来分配律是简算中的“常客”，学生就会误以为只要用了这个形式，就会使计算变得简便，却不知有时会适得其反。该题直接计算无比简单，用分配律反而变得异常复杂。

解决对策：

1.认真审题，培养良好的计算习惯。培养学生严谨审慎的审题态度，是杜绝错误的根本之道。有必要强调审题时的规定动作：一看、二画、三思。一看就是看清所有数字和符号；二画就是要标明运算的先后次序；三思就是反复斟酌是否具备简算条件，如果具备，该如何简算。

2.加强对比辨析，锻炼眼力。将相似度极高的算式集中起来进行对比辨析，让学生在一次次的辨别中认清它们之间的差异。促使学生对每个算式的显著特征都进行反复强化确认，直到每次遇到都能够严格区分，并迅速做出准确的判断和决策，对相关知识有全面深入的了解，建立稳固、准确的认知。如：

对比性练习将形式上相似性极强的算式放在一起，让细微的差别暴露在学生面前，并通过对比，使学生在心理上形成一种自然的防御机制，以后一遇到相似的情况，就会条件反射地产生警觉。

二、以错改错，拓展训练

在数学教学中，如果总是波澜不惊，那么学生的思维就会养成惰性，反应力和应激性也会不断弱化。但是如果在教学中制造悬念和冲突，学生探究的动机就会不断加强。学生的错误是制造悬念和冲突的绝佳资源，教师可以对错误进行巧妙处理，“将错就错”，从而使课堂不断翻转，让学生对犯错的教训铭记于心。

【案例2】常见的简算错误：

①99×72=100×72+72或99×72=（99+1）×72

②97×b+2×b+b=（97+2）×b

③（25+43）×4=25×4+43

④（125×7）×4=125×4+7×4

学生没有吃透分配律的内涵，只是机械地记住了外在形式。这可能是教师在教学时没有回归到加法和乘法的运算意义与关联上去解构乘法分配律，对乘法分配律的讲解没有深入到算理的高度，而是停留在形式上的变换和套用。

解决对策：

1.在教学乘法分配律时，教师应不断追寻本质。“律”即“规律”，是内在的、隐蔽的逻辑关联，“分”与“配”则是外显的表征。不妨板书如下：

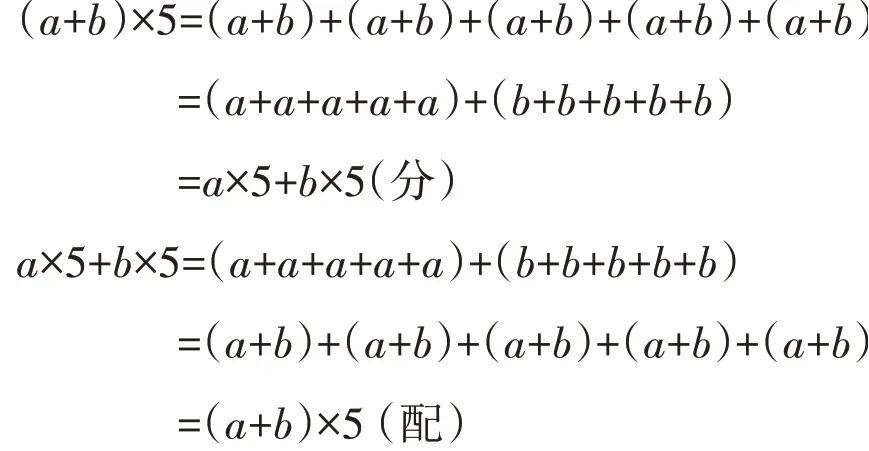
2.在理解算理的基础上增加拓展练习。

前三题，学生很快就能根据分配律的内涵与特征完成填数；最后一题是开放题，根据分配律的特征，必须出现一个“和”的形式，所以就要考虑将其中的一个因数分解成两个数之和，再与另一个因数相乘，这样既不改变算式的运算意义，也不改变结果，只是换了个形式，而这种形式恰好方便进行分配律运算。

三、自主纠错，对症下药

学生出现错误，教师要有容错的度量，要给学生试错的机会，既不能畏之如虎，也不能越俎代庖，强行插手纠错，而应该唤醒学生的认知，沿着他们的思想轨迹，循循善诱，让他们自己发现错误，转变思维方式。

【案例3】练习题：7313÷43。错解：17 余3。学生通过验算发现错误，但不知如何纠错，思维走入死胡同。此时教师展示如下算式，让学生计算后寻找差别，在对比辨析中，分清是非。

总结：商末尾的0 切勿遗漏，要做到“哪一位不够商1，就商0，留余数”。

【案例4】易错题：0.012÷0.25

这道题主要考查除数是小数的除法的小数点移位，其本质是考查学生对小数除法运算法则的掌握情况，即运用商不变定律将原式转化为整数除法，然后求出“共用商”。小数除法本就是学习难点，需要注意商的小数点的定位，而除数是小数的除法更是难中之难。根据错解的竖式可以判断，学生把被除数扩大了1000 倍，但是除数却没有同步变化，没有抓住除数“化整”的关键，从而出错。解题时，首要目标是将除数转化为整数，也就是最低要求是扩大100倍，而且是被除数、除数同步扩大。

解决对策：

在教学除数是小数的除法时，小数点的同步移位只是表象，商不变规律才是内涵，如果只关注小数点的移位，就很容易出错。移位的目的是将除数转化成整数，扩大时只有保证除数和被除数同步扩大，才能确保最后的商是通用商。先运用商不变定律进行算式转化：0.012÷0.25=1.2÷25，然后用竖式直接算出1.2÷25 的商，再进行小数点的移位，结果是0.048。

四、归类汇总，积累经验

大量教学实践表明，学生在学习中出现错误是正常现象。错误是学生积累经验的重要素材和来源，更是培育和发展学生辩证思维、批判思维的着力点。故而，在教学中，教师应对学生的各种错误进行归类汇总，并结合教学实际的需要，灵活运用错误资源，使之成为学生再学习、再研究的有效素材，从而让数学课堂教学更接近学生的实际学情，使学生的数学学习更具有针对性，也更加理性。

【案例5】简便计算：46×99+46。有部分学生出现错误：46×99+46=46×（100-1）+46=46×100-1+46=4600-1+46=4645。

学生的计算思路是：99 可以看成100-1，接下来用乘法分配律计算，就得出46×（100-1）+46，变化后是46×100-1+46。

解决对策：

学生出现错误的主要原因，不是对问题的解读有错误，也不是想法有问题，而是没有真正领悟乘法分配律的本质，没有从根源上来化解这类难点。因此，在这类问题的纠偏教学中，教师需要找准问题的源头，对症下药，让学生加深对乘法分配律的学习和领悟。

1.引导分析，多元化甑别。首先，组织学生反复观察自己的计算过程，让他们一边观察，一边思考。同时，指导学生应用相关的运算律来比对计算过程，促使他们加深对相关运算律的记忆，并对相应的计算过程进行反思。其次，开展学习联想，让学生自发地回忆之前学习中遇到过的相关题型，或是相关问题，促进学生深入思考。

2.综合比较，结构化初建。在学生自主思考的前提下，教师应重视对辩论活动的组织和开展，以便学生拓展学习视角，走出自我思考的封闭式圈子，学会倾听，并从中汲取养料，促进知识结构化。如针对案例4，有学生提出：46×（100-1）+46 中的46×（100-1）应该是100×46-1×46。也有学生提出：99 个46 加上1 个46，就是99+1 个46，这样计算更简便。

综上所述，学生计算出错的原因错综复杂，有的是思维定式造成的，有的是对运算性质和运算律的运用思维固化造成的，有的是对运算法则的理解不到位造成的，有时甚至是多种原因共同造成的。但是，无论哪种错误，只要诊断准确，制订科学合理的纠错对策，就能堵住漏洞，阻断错误的延续。