我国供水和用水相互影响的定性比较分析

宋 扬，陈 琛

（1.辽宁省水利水电勘测设计研究院有限责任公司，沈阳 110000；2.水利部发展研究中心，北京 100038）

1 前言

在水资源规划和供用水统计中，通常认为供水和用水之间是一种线性关系：在供需平衡的情况下，各个水源供给的总水量等于各行业使用水量之和。在此假定下，可以很容易根据行业用水量的变化计算供水量的变化，或反之；从而也可能认为如此简单的供水和用水关系是没有研究必要的。因此，目前国内对于供用水之间的关系研究多限于区域内供用水各自的结构变化[1-2]，供需水平衡[3-4]以及供水能力与需水量之间的差距分析[5]，对两者相互影响关系探究较少。

但实际上，供水和用水之间并不是一个简单的线性关系，而更可能体现为一种非线性关系，简单的供需平衡的线性关系结果其实是复杂的非线性影响的表现。基于以上认识，我们需要重新认识供水和用水之间的关系，研究供水和用水之间的相互影响规律，揭示用水量的供水驱动因素以及供水量的用水驱动因素。定性比较分析作为一种探求原因与结果逻辑关系的分析方法，最初应用于政治学和社会学领域[6-7]，后逐步应用至管理学[8]等其他学科，其能揭示导致某种结果发生的原因组合，可用以探求供用水之间的非线性关系。为此，本文应用定性比较分析方法（qualitative comparative analysis，QCA），利用1997—2016年我国供用水量的统计数据，分析供水和用水之间的相互影响关系，有助于补充我国供用水非线性关系研究的空白，帮助揭示我国供用水之间的相互影响规律。

2 定性比较分析方法

定性比较分析方法是一种数据分析技术，其逻辑基础源于Hume（1758），特别是来自J.S.Mill（1967），后来由Charles Ragin（1987）提出。定性比较分析基于布尔代数和集合论的思想，探求多个不同原因与某一特定结果之间的逻辑关系[9]。具体来说，定性比较分析将案例视为条件组态，用条件组态代替自变量、组态思想代替净效应思想、集合关系代替相关关系，通过案例找出所要解释的某一特定结果与条件组态的因果复杂性关系[10]。应用于供用水关系分析，可以研究行业用水量和总用水量对各水源供水量和总供水量的影响，反之也可分析供水量对用水量的影响。

定性比较分析的逻辑主要体现在对因果关系的理解上。定量研究假定社会现象的因果关系是线性的，而定性比较分析则假定社会现象的因果关系是非线性的，原因条件对结果的效应是相互依赖的，且同一个社会现象的发生可能是由不同的原因组合所导致的[11]。由于定性比较分析假定因果关系是多样、复杂且是可替代的，所以更加关注社会现象发生的多重原因组合，即一个条件对结果的影响同时取决于其他条件。

定性比较分析主要分为清晰集分析、多值分析和模糊集分析3种技术[12]。清晰集分析只能对变量进行0或1的赋值。模糊集分析可以在0和1之间任意进行赋值，能够同时处理清晰集数据和模糊集数据。因此，本文选择模糊集分析技术，并选用定性比较分析专用软件Fs/QcA2.0，以此得到导致供水和用水变化的条件组合。

模糊集分析首先对条件变量进行必要性检测，以检测是否为结果的必要条件。必要性检测有两个比较重要的衡量指标。第一个是一致性，指分析中所采用的所有案例共享的导致结果发生的程度，其计算公式如下[13]：

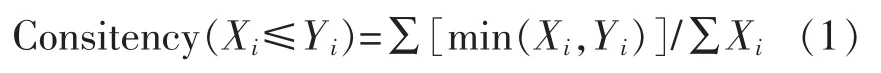
其中，X为条件变量组合的集合，Y为案例结果发生时的集合。

第二个是覆盖率，指条件解释结果出现的程度，其计算公式如下[14]：

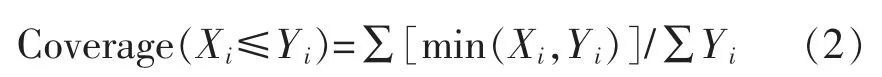
对于一致性来说，当得分超过0.9时，则可认为该解释变量是结果变量的必要条件。覆盖率范围从0到1，越靠近1，说明该条件组合越是保证达到结果Y的唯一路径[15-16]。

从逻辑关系上反映，一致性检测为必要条件分析，用来检测条件变量是否为结果变量的必要条件。必要条件是导致结果发生必须存在的条件，但是它的存在并不能保证结果必然发生，而真值表分析（条件组合分析）在本质上是充分性分析[1]。因此，覆盖率计算为充分条件分析，即条件发生，则结果必然发生。当一致性和覆盖度都满足标准要求时，X和Y构成充要条件；当一致性满足要求而覆盖率不满足时，X为Y的必要条件；当一致性不满足而覆盖率满足时，X构成Y的充分条件。

定性比较分析方法可用于汇总数据、数据一致性检查、假设和理论检查以及发展新的理论论断等，适用于处理中小样本的案例分析[17]。由于条件变量的组合呈指数形式，定性比较分析处理的条件变量需尽量控制在10个以内。

3 数据处理与变量赋值

本文分析我国不同水源的供水与不同行业的用水之间的相互影响关系。数据来源于1997—2016年《中国水资源公报》。按照其统计口径，供水量分为总供水量和地表、地下和其他水源供水量；用水量按照总用水量和工业、农业、生活和生态环境用水量统计归类。考虑到2003年以后才开始单独统计生态环境用水量，为保持数据系列的一致性，按照传统将生态环境用水量纳入生活用水量。同时，尽管采用了时间序列数据，但可以认为供水和用水相互影响的逻辑关系与时间无关，符合定性比较分析适用条件。

分析供水和用水相互影响规律的赋值可以考虑3类方式。一是基于年际水量变化赋值，如当年水量大于其前一年水量则赋值为1，小于则为0；二是相对于多年平均赋值，如某年水量大于该水量系列多年平均则赋值为1，小于为0；三是基于变化幅度赋值，如当年某水量年增长率大于该水量多年平均增长率，则赋值为1，如小于为0。比较3类方式，方式一反映了水量年际变化，但没有考虑与系列的关系；方式二和方式三都体现了与系列整体的关系，但方式二存在明显的时间因素；方式三基于年增长率与多年平均增长率之间的比较，在一定程度上去除了时间趋势。因此，本文采用方式三赋值：若当年对前一年的水量年增长率大于该水量系列多年平均增长率，则赋值为1，反之为0。

另外，为方便计算，将各个变量名称简化处理：以“TS”、“SS”、“US”和“OS”分别表示总供水量、地表水源供水量、地下水源供水量和其他水源供水量，以“TU”、“IU”、“AU”和“DU”分别表示总用水量、工业用水量、农业用水量和生活用水量；并以“*”表示逻辑“与”，“~”表示逻辑“非”。

4 用水对供水的影响分析

4.1 必要条件分析

表1显示了fs/QcA2.0的一致性分析结果。结果显示，结果变量为总供水量、地表水源供水量、地下水源供水量和其他水源供水量的所有3个条件变量（工业用水量、农业用水量和生活用水量）的一致性都在0.9以下，不能构成结果变量的必要条件。

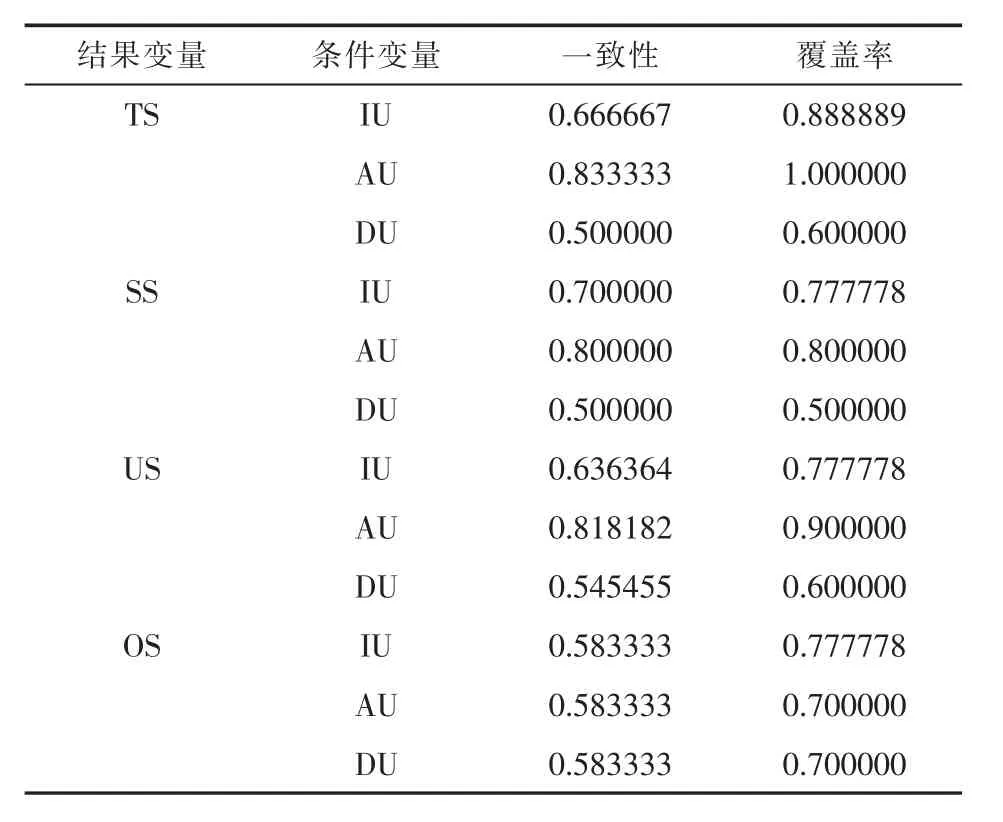
表1 用水对供水影响的单一条件变量的必要条件检测结果

4.2 条件组合分析

本部分根据构建的真值表，进行组合条件分析。真值表的构建需要首先设置一致性的临界值，通常不应低于0.75，一般推荐为0.8，本研究也设置为0.8[17]。

对条件变量的组合分析将得到3个输出方案，分别为复合方案（complex solution）、吝啬方案（parsimonious solution）和中间方案（intermediate solution）。复合方案是一种完全按照变量设置而产生的结果，没有使用“逻辑余项”（没有案例对应的组态）。吝啬方案在不评价和理性的情况下使用了所有的“逻辑余项”，但可能与事实不完全相符，但结果比较简单。中间方案则介于两者之间，纳入了有意义的“逻辑余项”，并且没有消除必要条件，部分情况下中间方案得到的方案同复合方案相同[17]。一般说来，中间方案优于复合方案和吝啬方案，本文结合复合方案与中间方案进行解释。

条件变量的组合分析方案结果包含条件组合、原始覆盖率（raw coverage）、唯一覆盖率（unique coverage）、解覆盖率（solution coverage）、一致性和解一致性（solution consistency）。原始覆盖率表示结果案例中该条件组合的覆盖比例。唯一覆盖率表示结果案例中被该条件组合唯一覆盖的比例。解覆盖率表示结果案例被所有条件组合覆盖的比例。解一致性代表这一个输出方案的所有条件组合的总一致性[17]。

表2显示了结果变量为总供水量的条件组合分析结果。复合方案、吝啬方案与中间方案完全相同，均只包含“AU”1个组合条件，该条件组合的一致性都为1。“AU”的组合表示为，当农业用水量年增长率超过其年均水平时，总供水量年增长率将超过其年均水平。该情况的原始覆盖率为0.833333，表示在1997—2016年当中，总供水量年增长率超过年均水平的所有年份中（在该案例中为12年），农业用水量年增长率超过其年均水平的年份（在该案例中为10年）所占的比例为0.833333。由于只有一种组合条件，所以解覆盖率也为0.833333。因此，对总供水量增加起决定的是农业用水量增加。案例显示，1999年、2001年、2004年、2005年、2006年、2008年、2009年、2010年、2011年、2012年和2013年属于这种情况。

表2 结果变量为总供水量的条件组合分析方案

表3显示了结果变量为地表水源供水量的条件组合结果。3个方案的条件组合完全相同，都为“IU*AU”，一致性为1。该组合表明当农业和工业用水量年增长率都高于年均水平时，地表水源供水量年增长率高于其年均增长率，该情况的原始覆盖率和解覆盖率都为0.600000。案例上发现，1999年、2004年、2005年、2006年、2011年和2013年属于此种情况。因此，对我国地表水源供水量增加起决定作用的是工业和农业用水。

表3 结果变量为地表水源供水量的条件组合分析方案

表4显示了结果变量为地下水源供水量的组合条件结果。3个方案完全相同，其原始覆盖率、唯一覆盖率和解覆盖率相同，解一致性和条件组合的一致性均为1。方案包含“~IU*AU”和“AU*DU”2个条件组合。“~IU*AU”表示，当农业用水量年增长率超过其年均水平和工业用水量年增长率都低于其年均水平时，地下水源供水量年增长率高于其年均水平，该情况的原始覆盖率为0.363636。“AU*DU”表示，当农业和生活用水量的年增长率都高于年均水平时，地下水源供水量年增长率也高于其年均水平，该情况的原始覆盖率为0.363636。2种条件组合的总的解覆盖率为0.545455。在AU的4种组合（分别为AU*DU*IU、AU*~DU*~IU、AU*~DU*IU和AU*DU*~IU）中，除了条件组合覆盖的3个组合（AU*DU*IU、AU*~DU*~IU、AU*~DU*IU）外，还剩下AU*~DU*IU1个组合：工业和农业用水量年增长率均高于年均水平但生活用水年增长率低于年均水平；这种条件组合里有3年（2004年、2007年和2011年）表现为地下水源供水量年增长率高于年均水平的结果，但有1年低于年均水平（2013年）。由于本研究设置一致性临界值为0.8，所以该条件组合的真值表赋值为0，没有包括在条件组合方案中。若将一致性临界值放松至低于0.75，结果变量为地下水源供水量的条件组合方案将构造出“AU”1个条件组合。因此，决定地下水源供水量超过其年均水平的条件是农业用水量年增长率超过其年均水平和工业用水量年增长率低于其年均水平、和农业和生活用水量年增长率都高于其年均水平；这些年份包括1999年、2001年、2004年、2005年、2006年、2008年、2009年、2010年和2012年。若适当放松临界值，则可以认为决定地下水源供水量增长的因素是农业用水量的增长。

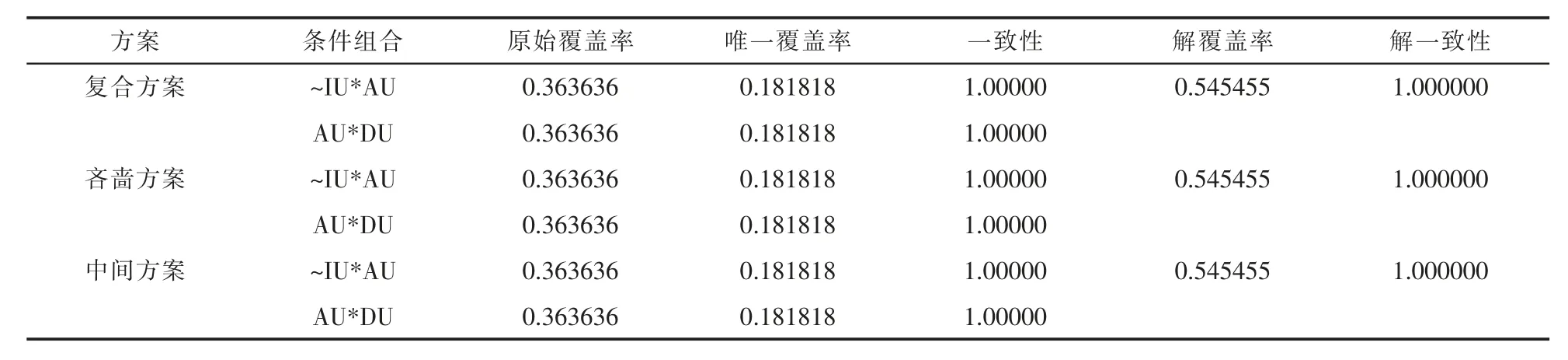
表4 结果变量为地下水源供水量的条件组合分析方案

表5显示了结果变量为其他水源供水量的条件组合结果。3个方案的条件组合完全相同，都为“IU*AU*DU”，一致性为1。该组合表明，当农业、工业和生活用水量年增长率同时高于年均水平时，其他水源供水量年增长率将高于其年均增长率。该情况的原始覆盖率和解覆盖率均为0.166667。因此，对我国其他水源供水量增加起决定作用的是三个行业用水量的共同增长。案例显示，2005年和2008年属于此情况。

表5 结果变量为其他水源供水量的条件组合分析方案

综合以上分析结果，基于1997—2016年供用水量年增长率和年均增长率的定性比较分析发现，我国供水量增长主要受工业和农业用水量增长的影响，而非生活用水量。在总供水量和地表、地下和其他水源供水量上表现为，若农业用水量年增长率超过其年均水平，总供水量年增长率将超过其年均水平；当工业和农业用水量年增长率同时高于年均水平时，地表水源供水量年增长率将高于年均水平；当农业用水量年增长率超过年均水平时，地下水源供水量年增长率在极大数年份高于年均水平；尽管其他水源供水量很小，但只有当工业、农业和生活用水量同时超过年均水平时，其他水源供水量年增长率才超过年均水平。这个结论似乎与实际不符，因为无论从累计增加幅度以及年均增长率，生活用水量年增加无疑是我国1997—2016年间用水量增加的主要因素，这主要是由于本文采用了年增长率和年均增长率作为研究对象，从而导致对供水量增加起决定作用的是工业和农业用水量，而非生活用水量。生活用水量提供了供水量增加的“基荷”，而供水量增加的“峰荷”由工业和农业用水量增加形成。

5 供水对用水的影响分析

本部分分析供水对用水的影响，也即是各水源供水量对行业用水量的影响。在分析中，总用水量以及工业、农业和生活用水量为结果变量，地表、地下和其他水源供水量为条件变量。

5.1 必要条件分析

表6显示了条件变量为地表、地下和其他水源供水量的一致性分析结果。总用水量为结果变量的分析显示，地表水源供水量和地下水源供水量的一致性均达到了0.9，其他水源供水量的一致性在0.9以下，再结合覆盖率分析，地表水源供水量的覆盖率大于地下水源供水量的覆盖率，表明地表水源供水量的解释力度要大于地下水源供水量的解释力度。这个结果说明地表和地下水源供水量都为总用水量的必要条件，说明当总用水量年增长率超过年均水平时，地表和地下水源供水量年增长率都将超过年均水平。

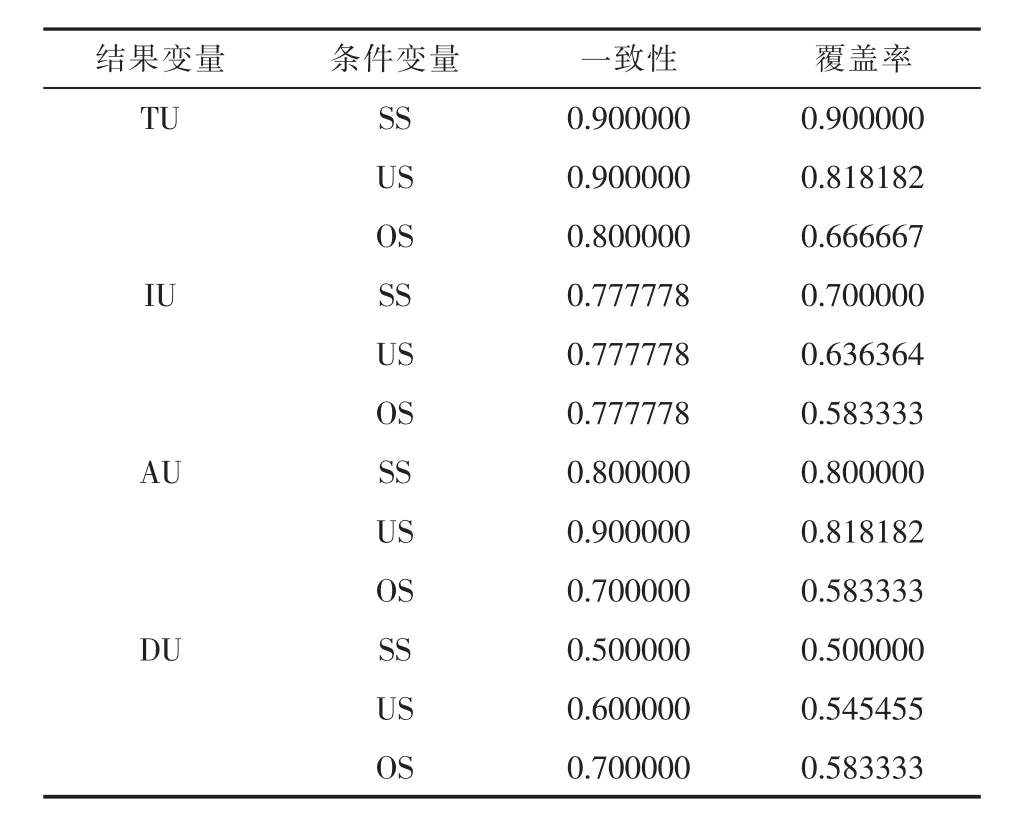
表6 供水对用水影响的单一条件变量的必要条件检测

表6同时显示了行业用水量为结果变量的分析结果。对于工业用水量，地表、地下和其他水源供水量的一致性都在0.9以下，不能构成工业用水量增长的必要条件。对于农业用水量，地表和其他水源供水量的一致性在0.9以下；地下水源供水量的一致性达到了标准，覆盖率为0.818182，说明地下水源供水量构成农业用水量的必要条件，表明当农业用水量年增长率超过其年均水平时，地下水源供水量将超过了其年均水平。对于生活用水量，地表、地下和其他水源供水量的一致性都在0.9以下，不能构成生活用水量的必要条件。

5.2 组合条件分析

表7显示了结果变量为总用水量的组合条件分析结果。3个方案完全相同，均只包含“SS*US”1个组合条件，该条件组合的一致性都为1。“SS*US”表明当地表和地下水源供水量年增长率同时高于年平均水平时，总用水量年增长率高于其年均水平，该情况的原始覆盖率和解覆盖率均为0.800000。案例分析发现，1999年、2004年、2005年、2006年、2008年、2009年、2010年和2011年属于此情况。但结合必要条件的分析结果，总用水量与地表和地下水源供水量均不构成充要条件。

表7 结果变量为总用水量条件组合分析方案表

表8显示了结果变量为工业用水量的条件组合分析结果。3个方案结果相同，都包含“~SS*US*OS”和“SS*US*~OS”2个条件组合。“~SS*US*OS”表示，当地下和其他水源供水量年增长率高于年均水平且地表水源供水量低于年均水平时，工业用水量年增长率高于年均水平，该情况的覆盖率为0.111111，一致性为1.000000。“SS*US*~OS”表示，当地表和地下水源供水量年增长率高于年均水平且其他水源供水量低于年均水平时，工业用水量年增长率高于年均水平，该情况的覆盖率为0.111111，一致性为1.000000。案例显示，2006年和2007年分别属于这两种情况。

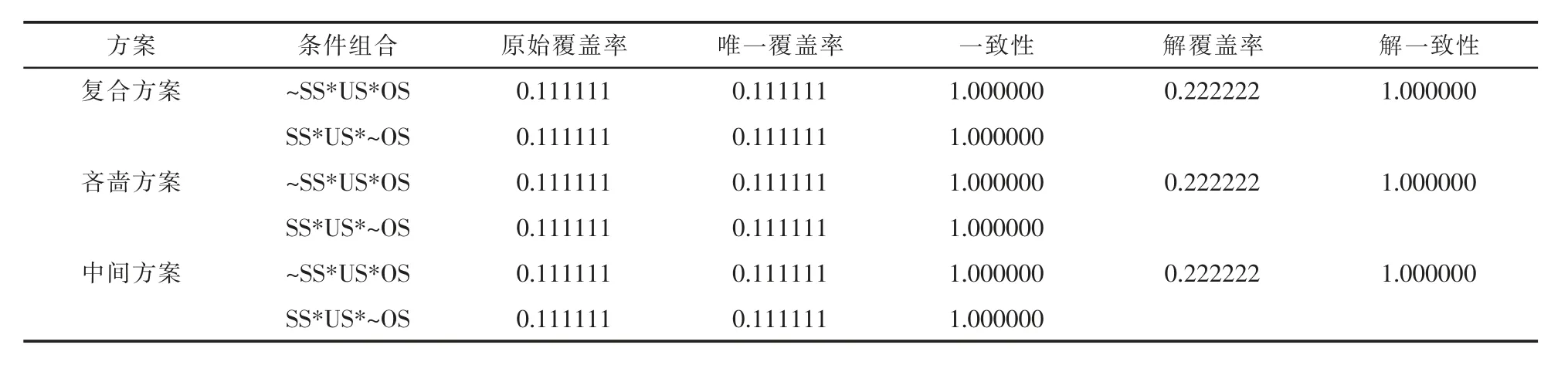
表8 结果变量为工业用水量的条件组合分析方案

由于每一条路径均只有一个案例，导致解覆盖率过低，故将结果变量设定为工业用水量的反向变量继续进行分析。表9显示了结果变量为工业用水量反向变量的条件组合分析结果。工业用水量反向变量为结果变量的3个方案结果也完全相同，3个方案的解的覆盖率为0.400000，解一致性为1.000000，包含“~SS*~US*OS”和“~SS*US*~OS”2个条件组合。“~SS*~US*OS”表示，当地表和地下水源供水量年增长率同时低于年均水平且其他水源供水量年增长率高于年均水平时，工业用水量年增长率低于年均水平，该情况的原始覆盖率为0.200000。“~SS*US*~OS”表示，当地表和其他水源供水量年增长率同时低于年均水平且地下水源供水量年增长率高于年均水平时，工业用水量年增长率低于年均水平，该情况的原始覆盖率为0.200000，也比较低。因此，结合工业用水量及其反向变量分析结果，没有一种水源或组合显示对其有显著影响。

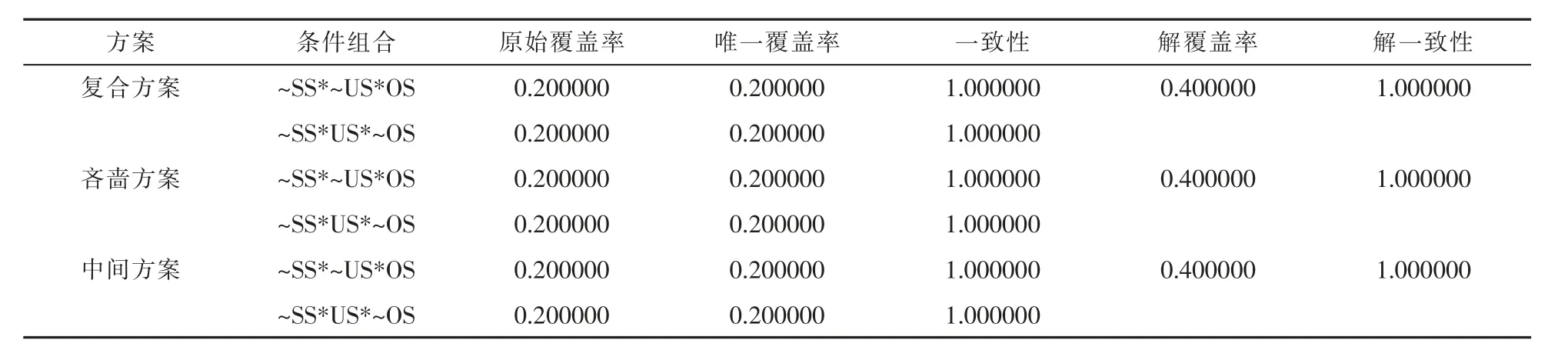
表9 结果变量为工业用水反向变量条件组合分析方案表

表10显示了结果变量为农业用水量的条件组合分析结果。3个方案结果完全相同，解覆盖率和解一 致 性为0.900000，包括 “US*~OS”和“SS*US”2个条件组合。“US*~OS”表示，当地下水源供水量年增长率高于其年均水平且其他水源供水量年增长率低于年均水平时，农业用水量年增长率超过其年均水平，该情况的原始覆盖率为0.300000。“SS*US”表示，当地表和地下水源供水量年增长率同时高于年均水平时，农业用水量年增长率超过其年平均水平，该情况的原始覆盖率为0.700000。案例显示，在1997—2016年中，1999年、2001年、2004年、2005年、2006年、2008年、2009年、2011年、2012年均为这两种情况。但结合必要条件分析结果，农业用水量与地下水源供水量不构成充要条件。

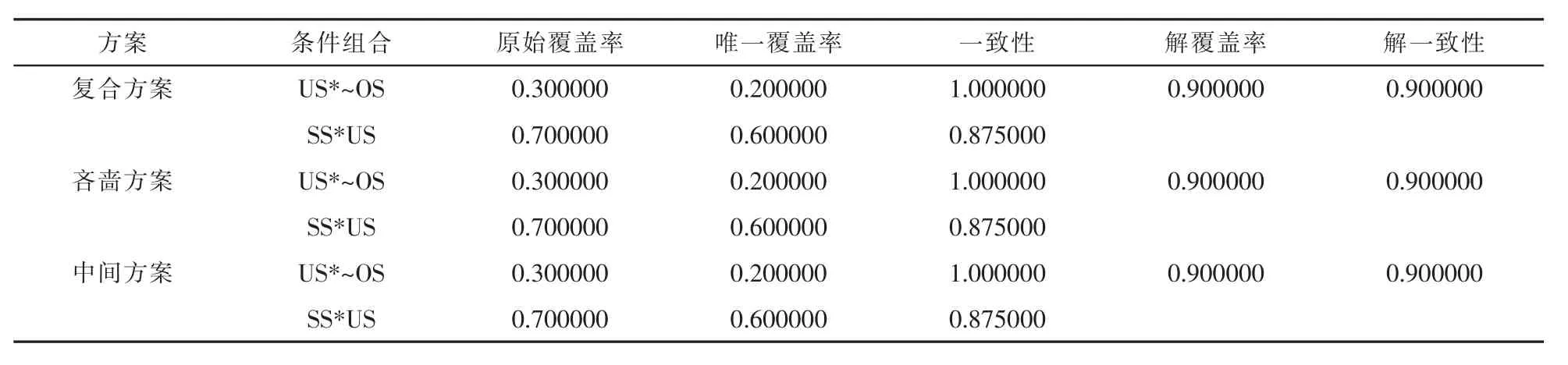
表10 结果变量为农业用水的条件组合分析方案表

表11显示了结果变量为生活用水量的条件组合分析结果。3个方案完全相同，解覆盖率为0.111111，解一致性为1.000000，均只包括“~SS*US*OS”1个条件组合。“~SS*US*OS”表示，地表水源供水量的年增长率低于其年均水平且地下和其他水源供水量高于年均水平时，生活用水量年增长率高于年均水平，该情况的覆盖率为0.100000。由于该路径只包含1个案例，解覆盖率过低，需要将结果变量设定为生活用水的反向变量继续进行分析。

表11 结果变量为生活用水量的条件组合分析方案表

表12显示了结果变量为生活用水量反向变量的条件组合分析结果。复合方案与中间方案相同，吝啬方案在它们的基础上去掉了1个变量，3个方案的解覆盖率均为0.111111，解一致性均为1.000000。复合方案和中间方案均只包括“SS*US*~OS”1个条件组合。该组合表示，当其他水源供水量年增长率低于其年均水平且地表和地下水源供水量高于年均水平时，生活用水量年增长率低于年均水平，该情况的覆盖率为0.100000。该路径只包含一个案例，解覆盖率比较低。

表12 结果变量为生活用水量的反向变量的条件组合分析方案表

综合表11、表12与表6的结果说明，生活用水量不受地表、地下和其他水源供水量的影响。这与供水量的分析结果相对应，我国1997—2016年供水量增加主要受工业和农业用水量的影响，而不受生活用水量的影响。

综合以上分析结果，基于1997—2016年供用水年增长率和年均增长率的定性比较分析发现，我国供水对用水的影响表现为：尽管总用水量年增长率超过其年均水平将导致地表和地下水源供水量超过年均水平，但只有地表和地下水源供水量同时超过年均水平，总用水量年增长率才超过其年均水平；工业用水量的影响因素比较复杂，无论其年增长率增加或减少，并没有表现出显著的水源特性；尽管农业用水量年增长率超过其年均水平将导致地下水源供水量超过其年均水平，但只有地表和地下水源供水量年增长率同时超过年均水平，农业用水量年增长率才超过其年均水平；而生活用水量年增长率不受地表、地下和其他水源供水量的影响。

6 结论

本文基于非线性假设，应用定性比较分析方法对供水水源和行业用水量之间的相互影响关系进行了探索，从另一个视角揭示了两者之间的联系，并具体分析了我国1997—2016年供水量和用水量之间的相互影响。

研究表明，定性比较分析方法基于因果关系理解的逻辑分析，可以很好应用于供水和用水之间的相互影响关系分析，我国1997—2016年的数据分析结果符合实际情况。

基于水量年增长率和年均增长率比较赋值的我国1997—2016年供用水数据定性分析发现，我国供水量增长主要受工业和农业用水量增长的影响：若农业用水量年增长率超过其年均水平，总供水量年增长率将超过其年均水平；当工业和农业用水量年增长率同时高于年均水平时，地表水源供水量年增长率将高于年均水平；当农业用水量年增长率超过年均水平时，地下水源供水量年增长率在极大数年份高于年均水平；只有当工业、农业和生活用水量同时超过年均水平时，其他水源供水量年增长率才超过年均水平。地表和地下水源对用水的影响显示了同等重要性：只有地表和地下水源供水量同时超过年均水平，总用水量和农业用水量年增长率才超过其年均水平；而工业用水量和生活用水量并不受水源的影响。□