深覆盖层的水闸长效运行结构应力分析

张方宁，赵 琛，王鸿飞，祝福源

（1.南京市水利规划设计院股份有限公司，江苏 南京 210001；2.河海大学水利水电学院，江苏 南京 210098；3.水发规划设计有限公司，山东 济南 250100）

1 引言

水闸是中小型河流，湖泊，水库，山塘，入海口等控制调节流量、灌溉，防潮防洪的主要控制性工程[1-2]。水闸作为水利工程的系统工程中的重要一环，是打通顺畅江河湖海的毛细血管的关键，对推进新时代水利工程现代化具有重要意义[3]。所以确保水闸工程长效运行的安全十分必要，特别对于平原地区[4]，深覆盖层较厚的水闸，随着服役时间的推长，其运行状态的演变一直是研究的热点和难点[5-6]。如崔朕铭等人[7]建立了以软土水闸各结构的强度水平为约束条件的优化设计数学模型，进而分别求得了水闸整体结构优化设计方案和闸室结构优化设计方案；李火坤等人根据软基水闸的特点构建了底板脱空动力学反演模型构建与试验验证[8]，并基于模态参数及BAS-PSO优化了软基水闸有限元模型参数[9]；张宇等人[10]则以桩基为切入点研究了软土地基下水闸底板有限元分析的模拟方法。由上述研究可知，对于深覆盖层软土地基的研究成果颇多，但目前深覆盖层对水闸长效运行的影响有待进一步研究。由于深覆盖层的模拟决定了计算结果的精度水平，所以本文采用已经广泛应用的理想弹塑性模型模拟深覆盖层土基。为了解决水闸底板和土基之间协调变形的问题，引进标准库伦摩擦模型模拟地基与底板的接触性态。针对实际工程，通过三维有限元计算水闸运行20年的结构应力变化情况并分析其变化特性。

2 水闸结构计算模型与实现步骤

2.1 土体本构模型及初始地应力场模拟

土体的本构模型主要有弹性模型、超弹性模型、次弹性模型、粘弹性模型、弹塑性模型、粘弹塑性模型、内蕴时间塑性模型等。其中弹塑性模型较之前四种模型更能反映土体的变形特性；较之后两种模型，弹塑性模型使用方便，计算精度相差不大。为了更好地模拟闸基覆盖层的结构变形，并且对于深覆盖层土体，同一土层可以近似为同质土层，所以覆盖层的土体本构模型采用理想弹塑性模型。该模型的应力-应变的增量关系[11-12]为：

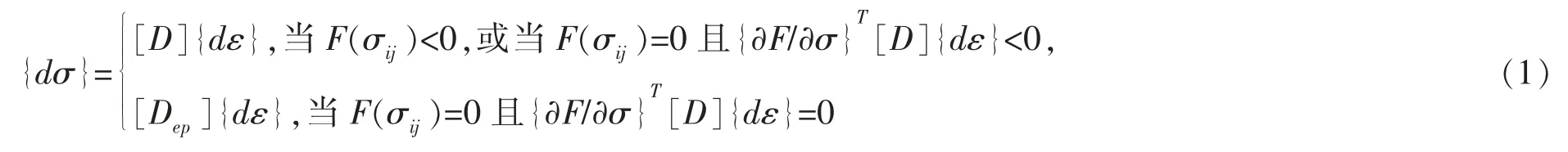
式中，［D］为各向同性弹性矩阵；［Dp］为材料的塑性矩阵；F（σij）为屈服函数，Q（σij）为塑性势函数。其中［Dep］、［Dp］分别为

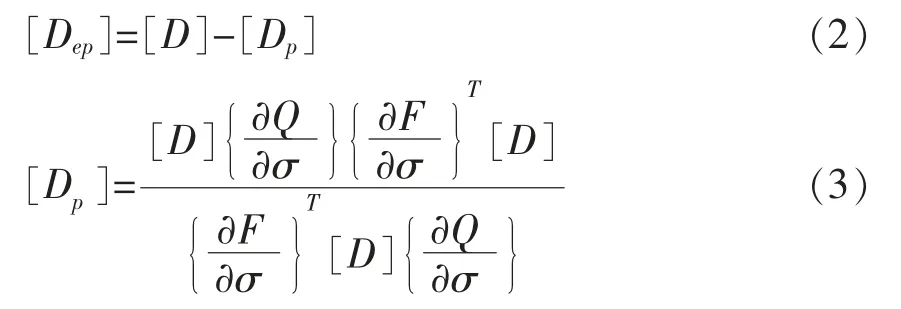
通常，水闸工程区域构造活动不活跃，地基土是深厚的粘土及砂土，因此可认为地应力是自重引起的，可应用的弹性半空间重力作用下求解应力分量的原理来模拟地应力场。为研究自重作用下地基应力状态，可在地基土中取微小单元体。由于是空间问题，其应力和应变可用x、y、z的下小标表示，则在该微小单元体六个面上作用的法向应力σx、σy、σz和剪应力τzx=τxz，τxy=τyx，τzy=τyz， 如图1所示。

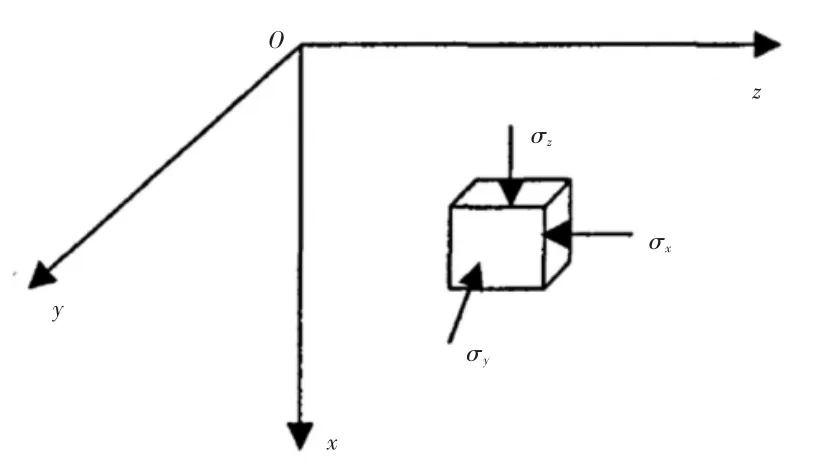
图1 半无限弹性空间的单元的受力状态

当土层为分层土时，假定地基土为水平向均质同性的弹性半空间，土层分界面为水平面，则第n层土底面的自重应力为：

式中：z是所考察点到地表面的埋深距离；σz，σx分别为竖向和水平方向的土的自重应力；γ，h分别为第i层土的天然重度（地下水位以下取有效重度）和厚度；n为天然地面起至所要计算深度之间的土层数；K0为第n层土的静止侧压力系数。

2.2 接触单元的模拟

接触问题的求解是一种高度非线性行为，水闸结构材料与土体材料的物理性质相差较大，结构在荷载作用下，其接触面上会产生错动滑移或开裂，不符合位移连续性假定，需引入接触单元来模拟混凝土结构与土体材料之间的接触，因此采用面-面接触单元模拟水闸结构和地基土接触面以反映其变形特性。

根据水闸与土体间滑动的具体规律，标准库伦摩擦模型符合上述接触单元的受力特性[13]。标准库伦摩擦模型是通过定义接触对实现的，接触面一个定义为主面，另一个定义为从面，一旦发生接触，从面上的点就会和主接触面建立接触约束，形成接触对。当生成三维接触单元，接触约束是通过内部的接触单元来实现。通过定义接触面的本构关系，描述接触界面的摩擦力学特征，具体可通过定义接触面的摩擦系数和切向刚度等参数来定义[14]。若等效摩擦应力τeq小于临界剪应力τcrit（与接触应力p成比例），则两物间无相对运动发生；反之，则开始发生相对运动。即：τeq＜τcrit则无滑动；τeq=τcrit则开始滑动。其中，，（P为接触点的接触应力或接触压力，μ为摩擦系数）；τeq为滑动速率。

本次计算模型在水闸土基与闸室底板之间设置接触，选择闸室底板作为主控接触面，地基土体作为从属接触面，接触间的摩擦系数取0.56。

2.3 水闸基本荷载及计算步骤

水闸基本荷载一般包括水闸及上部设备的自重、水重、静水压力、扬压力等。荷载计算方法如下：

（1）水闸及上部设备的自重

水闸结构自重按结构尺寸和材料密度计算确定：

式中，m为结构质量，g为重力加速度。

（2）水重

对应工况及荷载组合情况下，则作用于水闸底板上的水重：

式中，γ为水的容重；H为对应水深。

（3）静水压力

对应工况及荷载组合情况下，则施加在闸门、闸墩、翼墙等部位上的静水压力：

式中，γ为水的容重；H为对应水深。

（4）扬压力

水闸底板受到的扬压力为付托力和渗透压力之和。水闸底板受到的扬压力，采用面力施加。浮托力依据闸室底板完全浸入水中部分体积V排确定：

深覆盖层水闸三维有限元结构计算基本步骤主要分为以下四步：

第一步：计算水闸地基土在自身重力作用下的初始地应力，并导出各单元质心点应力；

第二步：将初始地应力场导入水闸及地基土模型中，保持水闸地基岩土原始应力水平并使其位移接近于零，以逼近真实状态；

第三步：建立通用静力分析步，分别模拟不同运行年份的水闸的结构受力情况；

第四步：对比分析水闸结构的应力变化情况，研究其对结构的安全状态。

3 工程案例

3.1 计算模型与边界约束条件

某水闸枢纽位于华东地区长江流域，该水闸为节制闸，共3孔，每孔净宽10m，总净宽30m，采用平面钢闸门，启闭机采用卷扬式启闭，设计排洪流量309m3/s。该水闸三维有限元模型如图2所示，模型的范围为横河向，自南岸挡土墙向南延伸50m，自北岸挡土墙向北延伸50m；顺河向，自水闸底板上游侧向上游延伸120m，自水闸底板下游侧向下游延伸80m；垂直方向，自底板高程向下延伸至岩基础。

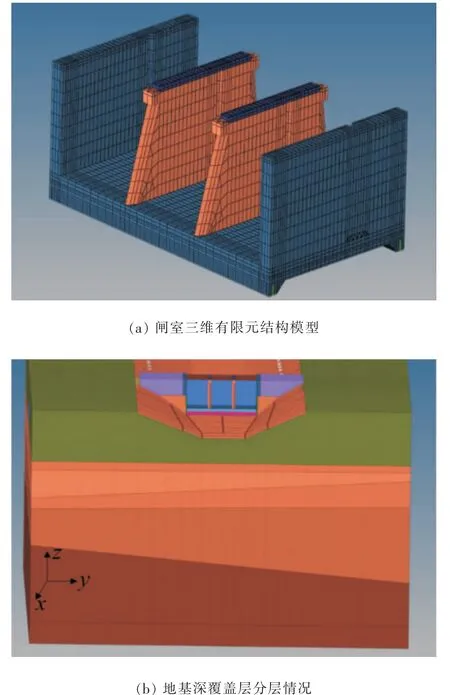
图2 水闸三维有限元计算模型

其中模型x轴沿河流方向指向下游，y轴在横河向方向由南岸指向北岸，z轴垂直指向上方，地基边界采用法向约束，其余为自由边界。其中水闸单元数为68 470，护坡单元数为25 641，地基单元数为239 314，共计333 425个。

3.2 材料参数与计算假定

水闸、地下连续墙等均采用C20混凝土，护坡采用M15浆砌石（块石砌石体饱和抗压强度60MPa），钢板闸门采用Q235钢。在有限元模型中，水闸及桥墩结构采用线弹性本构模型，其中地下水位以下土层采用浮重度、地下水位以上土层采用天然重度。根据相关规范和地勘报告，水闸三维有限元计算模型混凝土和地基土层物理力学参数分别见表1和2。

表1 各材料力学参数

表2 各土层力学参数

3.3 计算结果及分析

在输入模型参数后，则可以计算水闸运行20年的水闸结构应力情况。水闸结构应力计算结果如图3—图6所示。

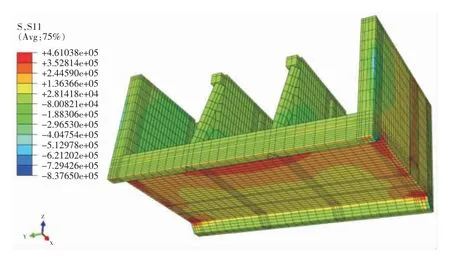
图3 运行第1年水闸结构应力（单位：Pa）

图6 运行第20年水闸结构应力（单位：Pa）

由图可知：从应力分布方面，底板下游中间拉应力最大，为水闸结构最不利区域；边墩的中间位置的拉应力较大，这两部分是结构安全评价中重点评价的对象；其他位置较为安全。从运行时间来看，最大拉应力由变大的趋势，但总体幅度不大，说明深覆盖层对结构整体应力的影响不大，这主要与水位和运行时间有关。

通过水闸运行资料可知，该水闸自建设运行以来，运行平稳，变形和应力趋于收敛，这与上述计算结果相符。但伴随水位的升高和运行时间的推进，结构变形有缓慢增长的趋势。在运行时效方面，水闸结构的耐久性受材料、施工质量、维护质量和水位的调节周期等因素综合影响。

图4 运行第5年水闸结构应力（单位：Pa）

图5 运行第10年水闸结构应力（单位：Pa）

4 结论

（1）理想弹塑性模型能够模拟长效运行的水闸覆盖层地基，标准库伦摩擦模型可以表征底板和地基间的接触关系。

（2）由工程算例可知：水闸的结构应力分布符合水闸受力特性。在平均水位作用下，结构应力变化幅度不大。在强度方面，深覆盖层对于水闸整体长效的结构应力影响不大的，但依然要综合其他方面，如位移、渗流，评估其安全性和除险加固的必要性。

（3）由于水闸的水位是动态变化的，本文为提高计算效率而简化采用了年平均水位进行模拟，下一步可以采用动态水位进行计算模拟以提高水闸结构模拟的准确度。□