加劲环式地下埋管非线性有限元屈曲分析

伍鹤皋，胡 悦，石长征，鲁志航，李月伟，汪碧飞

(1.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.长江勘测规划设计研究有限责任公司，湖北 武汉 430015)

0 引 言

对地下埋管进行抗外压稳定分析可归结为计算其临界压力，且多按平面问题进行分析，即认为钢管是均匀介质中的弹性圆环。目前关于地下埋管抗外压稳定分析的计算理论和方法仍主要停留在Amstutz、Jacobsen、Mises等学者的解析公式和经验公式上。地下埋管在结构上可分为光面管和加劲环式钢管，两者的抗外压稳定计算方法略有差别。关于加劲环式地下埋管的抗外压稳定，需同时满足加劲环间管壁和加劲环自身的稳定。其中，加劲环间管壁的临界压力一般采用Mises公式[1]，并得到我国水电站压力钢管设计规范、美国ASCE压力钢管规范[2]和日本闸门钢管技术标准[3]以及学者Amstutz等人的广泛推荐和采用。

对于加劲环自身的抗外压稳定，有很多学者提出了各自的计算理论和方法，概括起来常用的主要有Amstutz法、Jacobsen法、Svoisky法、NB/T 35056—2015《水电站压力钢管设计规范》中的强度公式。其中，Amstutz法认为对于埋藏式压力钢管加劲环的临界压力，仍可采用与埋藏式光面管临界压力相同的计算公式，只是在计算加劲环截面特性时考虑了等效翼缘以外的管壁荷载对加劲环临界压力的影响，即偏保守地假定加劲环之间的所有外压力均由加劲环和等效翼缘以内的管壁承担[4-5]。Jacobsen法与Amstutz法的基本假定相同，但它针对Amstutz法中存在的一些问题，如简化方法的精度和适用范围问题、管壁等效翼缘宽度的取值等作了优化[6-7]。Svoisky法与Amstutz法及Jacobsen法的假定有所不同，它没有考虑加劲环承担等效翼缘以外管壁失稳可能传来的外压，而仅仅是加劲环本身局部失稳时对应的临界压力，导致计算所得的临界压力偏高，且缺乏模型试验和实际工程的检验[8]。我国NB/T 35056—2015《水电站压力钢管设计规范》采用强度条件来估算加劲环的稳定，认为当整个有效截面的环向应力达到钢材的屈服强度时，加劲环即发生失稳[9]。该公式计算过程虽然简单，但一些工程实例都说明按强度公式估算的设计结果偏于保守。

除了以上几种常用的计算方法外，国内一些学者也做了研究工作并提出了开拓性的方法。一是赖华金-范崇仁提出的临界压力公式[10]，该公式在弹性理论的基本假定上还作了4个基本假定，运用壳体稳定理论推导出临界压力的计算公式。虽然此公式的计算结果与他们的试验成果较为一致，但由于其假定的边界条件过于严格，在实际工程中未能得到进一步推广。二是刘东常教授提出的半解析有限元法[11]，该方法沿管轴向将结构离散为圆柱壳单元和圆环板单元，沿周向采用解析法描述形函数，对加劲环式钢管整体进行稳定分析。但该方法没有考虑钢管与回填混凝土之间的初始缝隙和材料本身存在的缺陷等问题，其适用性也有待进一步研究。

鉴于以上现状，本文在考虑初始缺陷、初始缝隙及材料非线性的基础上，采用ABAQUS有限元软件，对加劲环式地下埋管结构进行线性和非线性屈曲分析，并探讨了不同初始缺陷、初始缝隙值、加劲环间距和加劲环高度对加劲环式地下埋管临界压力的影响，最后对地下埋管抗外压稳定分析的解析法和有限元法进行了比较分析，提出地下埋管抗外压稳定设计的新思路。

1 有限元计算模型

某水电站地下埋管钢管内半径2.5 m，强度计算确定的管壁厚度24 mm，加劲环厚度与钢管管壁厚度相同，即24 mm，加劲环高200 mm，间距取2 000 mm。钢管外回填混凝土厚0.6 m，围岩范围以大于10倍开挖半径为原则，故整体模型宽度与高度均取60 m。利用ABAQUS软件对上述地下埋管进行建模，并取加劲环个数为5的加劲环式地下埋管作为计算模型。

回填混凝土及围岩均采用实体单元进行模拟，并当作线弹性材料考虑。钢管和加劲环均采用壳单元进行模拟，由于薄壳结构的屈曲分析属于大变形问题，因此钢材采用非线性本构。钢材采用Q345钢材，屈服强度为335 MPa，钢材的应力应变关系采用双折线模型。图1和图2分别为加劲环式地下埋管的整体模型和带加劲环的钢管有限元网格示意。

图1 加劲环式地下埋管整体模型

图2 加劲环钢管有限元网格

2 加劲环式地下埋管屈曲分析

根据是否考虑非线性问题，ABAQUS提供了线性屈曲和非线性屈曲两种分析方法。在实际工程中，材料经常由于几何缺陷和物理缺陷等因素使得理想弹性结构的屈曲基本不存在，且地下埋管结构还应考虑回填混凝土和钢管的相互作用，因此这是一种典型的非线性行为。非线性屈曲分析是把增量非线性有限元法与特征值屈曲求解相结合的一种静力分析方法，可以充分考虑材料、几何和接触等非线性行为，结果比线性屈曲分析更符合实际。

2.1 初始缺陷的引入

钢管在制造、加工和运输等过程中往往会产生一定的缺陷，并且在长期运行中还会产生不同程度的磨损和锈蚀，这些缺陷、磨损和锈蚀都会降低钢管的抗外压能力，可能使钢管在这些位置发生局部屈曲而降低整体结构的屈曲临界压力。本文在非线性屈曲分析之前先通过线性屈曲分析得到钢管结构的屈曲失稳模态，并以第一阶屈曲失稳模态为基础，按一定的比例因子来创建初始缺陷，一般取钢管管壁厚度的1%[12]。在非线性屈曲分析之前读入初始缺陷并更新模型，这样就可将初始缺陷引入非线性屈曲分析。

2.2 回填混凝土约束作用的考虑

钢管和回填混凝土之间的相互作用通过设置接触来实现，即在钢管与回填混凝土之间设置接触单元，并利用接触单元的初始间隙值来模拟钢管与回填混凝土之间的初始缝隙。在屈曲分析中，外压荷载是逐渐增加的，当外压荷载较小时，钢管发生向内凹的变形。随着外压荷载的增大，钢管产生微小的褶皱，向内凹和向外凸的变形均有存在。在管壁外凸变形量小于初始缝隙值的过程中，钢管与回填混凝土未发生接触，因此钢管不受回填混凝土的约束作用；当管壁外凸变形量大于或等于初始缝隙值时，外凸变形的管壁将与回填混凝土接触，此时钢管受到回填混凝土的约束作用，一直到钢管发生屈曲失稳。

为了便于分析回填混凝土约束作用对地下埋管抗外压稳定能力的影响，设置一组不考虑回填混凝土约束作用的方案(明管方案)，将其与考虑回填混凝土约束作用的方案(埋管方案)进行对比。其中埋管方案中钢管与回填混凝土间的初始缝隙值取钢管内半径的5/万，即1.25 mm。

图3为第3个和第4个加劲环之间管壁某节点A和加劲环某节点B的位置示意，绘制两种方案下节点A和节点B的荷载—径向位移曲线如图4。从图4可以看出，两种方案外压力从0开始增加，管壁节点A的径向位移均逐渐增大，且在外压力较小时管壁节点A的曲线相同。当外压力增大至2.41 MPa时，明管方案管壁节点A的曲线开始下降；而埋管方案管壁节点A的曲线仍有一段小幅的上升阶段，在外压力达2.56 MPa时才出现下降。这是因为在埋管方案下，当外压力增大至2.41 MPa时管壁与回填混凝土接触，回填混凝土在一定程度上限制了管壁进一步的外凸变形，因此提高了管壁的屈曲临界压力。从开始加载直到管壁发生屈曲失稳，两种方案下加劲环节点B的径向位移均很小，且基本随外压力的增加呈线性增大，说明加劲环仍未发生失稳。总体而言，埋管方案和明管方案下的屈曲临界压力分别为2.56 MPa和2.41 MPa，考虑回填混凝土的约束作用后，钢管的屈曲临界压力提高了约6.22%。

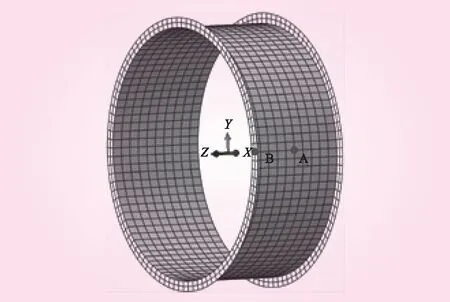
图3 特征节点示意

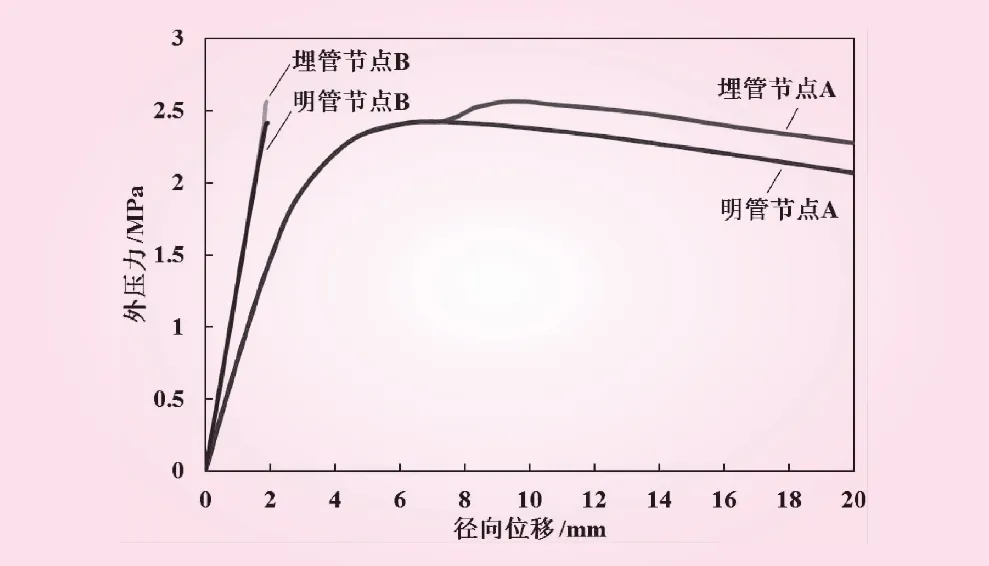
图4 特征节点荷载-径向位移曲线

图5为明管方案和埋管方案下钢管发生屈曲失稳时的整体径向位移云图。由图5可知，在钢管发生屈曲失稳时，明管方案下管壁内凹和外凸的最大位移分别为8.12 mm和1.94 mm，埋管方案下管壁内凹和外凸的最大位移分别为9.51 mm和1.50 mm。相比明管方案，埋管方案下管壁外凸的最大位移略有减小，而内凹的最大位移有所增加。这是由于埋管方案考虑了回填混凝土的约束作用，管壁的外凸变形受到一定的限制，同时提高了钢管的屈曲临界压力，故允许管壁有更大的内凹变形。

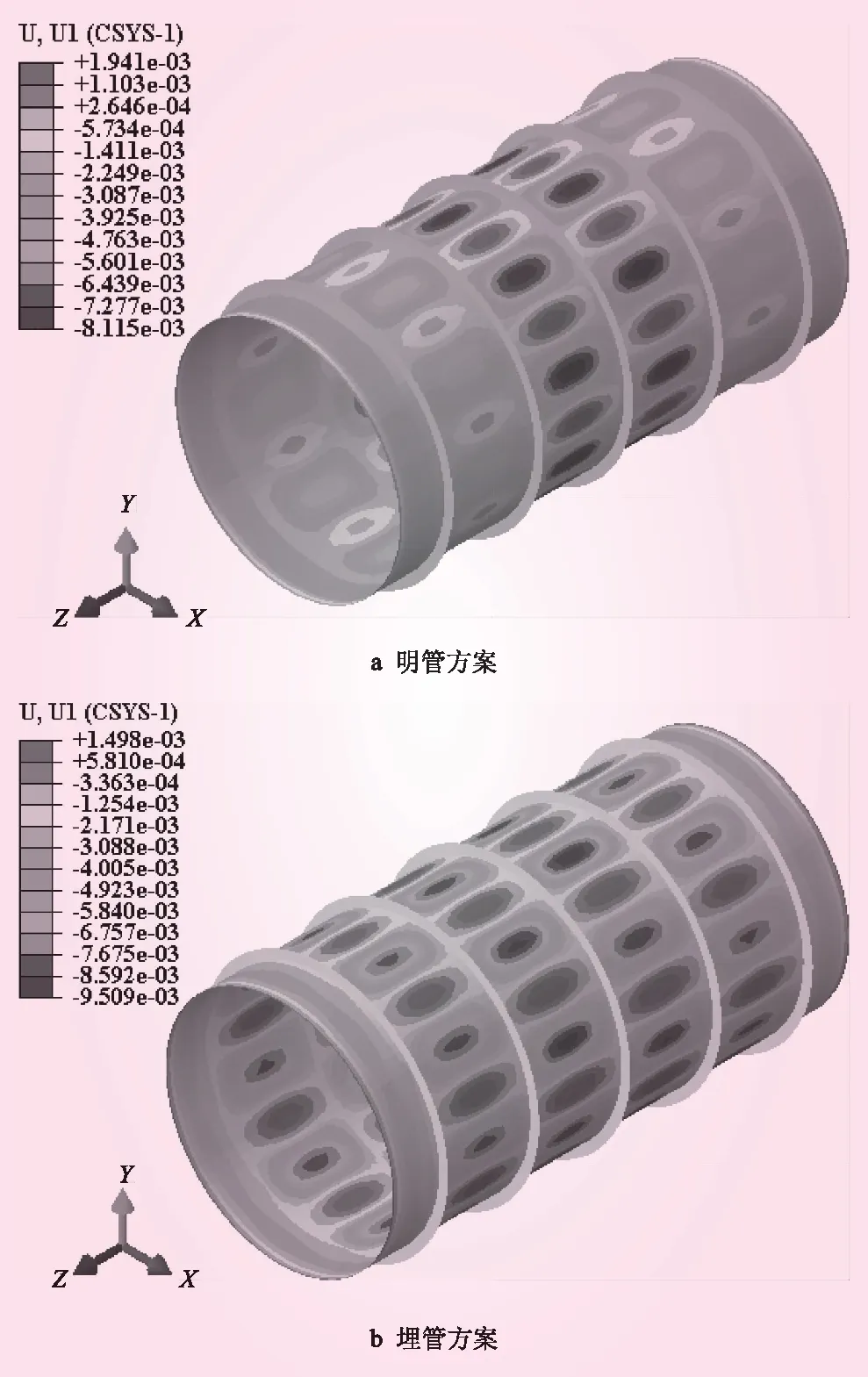
图5 钢管整体径向位移云图(单位：m)

图6为埋管方案下钢管发生屈曲失稳时与回填混凝土的接触状态。由图6可知，钢管与回填混凝土大部分区域均处于脱开状态。在局部位置，当管壁外凸的位移超过了钢管与回填混凝土的初始缝隙值(1.25 mm)后，管壁与回填混凝土接触，回填混凝土将对这些区域起到一定的约束作用。

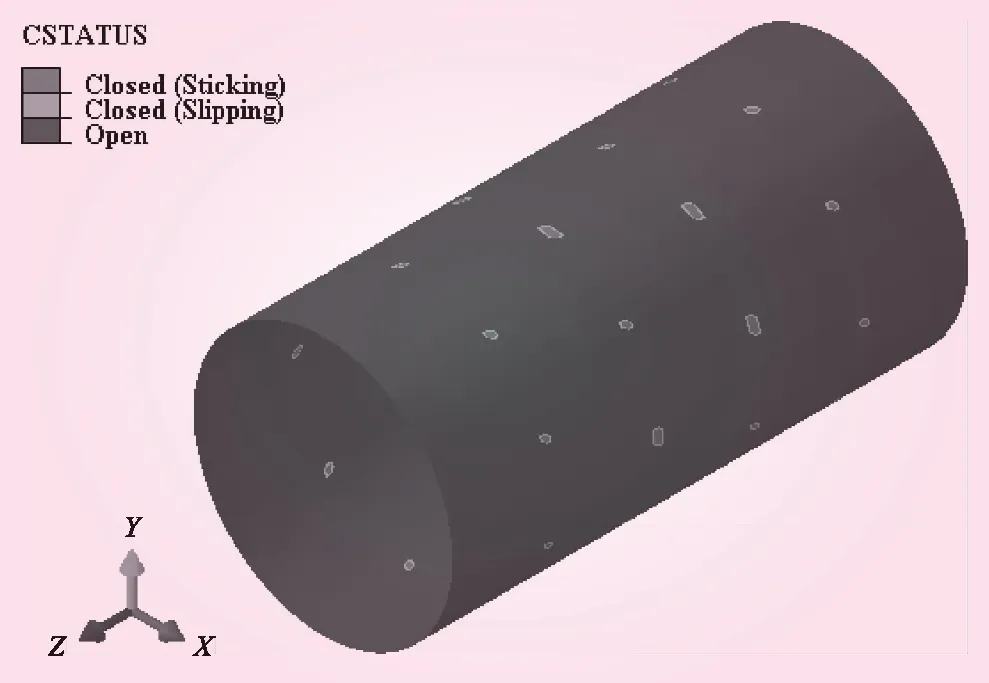
图6 埋管方案下钢管与回填混凝土接触状态

3 加劲环式地下埋管临界压力的影响因素

大量工程实践表明，影响加劲环式地下埋管临界压力的因素有很多，例如钢管的初始缺陷、钢管与回填混凝土间的初始缝隙值、加劲环间距、加劲环高度、钢管的管壁厚度等[13]，本节将针对其中几个因素对加劲环式地下埋管临界压力的影响展开研究。

3.1 初始缺陷

为研究初始缺陷对加劲环式地下埋管临界压力的影响，本小节以线性屈曲分析中的第一阶屈曲失稳模态为基础，针对不同的初始缺陷幅值进行非线性屈曲分析，计算结果如表1所示。

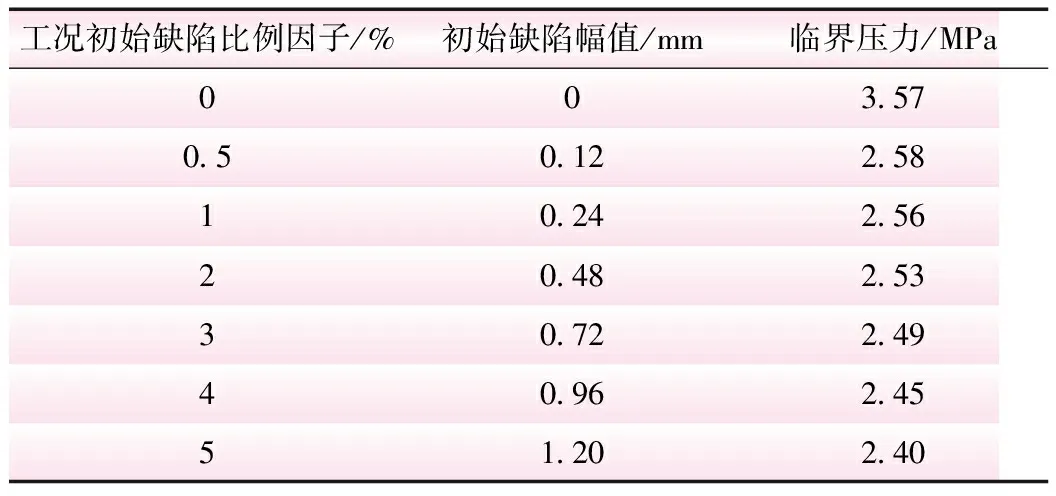
表1 不同初始缺陷下加劲环式地下埋管临界压力

从表1可知，在不考虑初始缺陷的条件下，加劲环式地下埋管的屈曲临界压力较大，数值达3.57 MPa。考虑初始缺陷后，钢管的临界压力明显降低；引入1%的初始缺陷后，钢管的临界压力为2.56 MPa，与未考虑初始缺陷的临界压力相比降低了约28.29%；随着初始缺陷幅值的增加，钢管的屈曲临界压力基本呈线性下降的趋势。

3.2 初始缝隙值

为研究初始缝隙值对加劲环式地下埋管临界压力的影响，在初始缺陷幅值取0.24 mm的基础上，选择不同的初始缝隙值进行计算，得到不同初始缝隙值下钢管的屈曲临界压力如表2所示。不同初始缝隙值下钢管与回填混凝土的接触状态如图7所示。

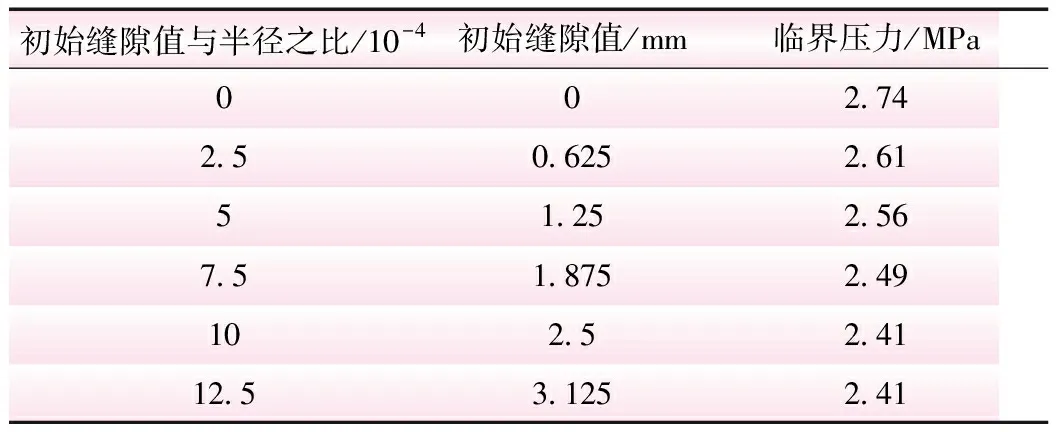
表2 不同初始缝隙值下加劲环式地下埋管临界压力

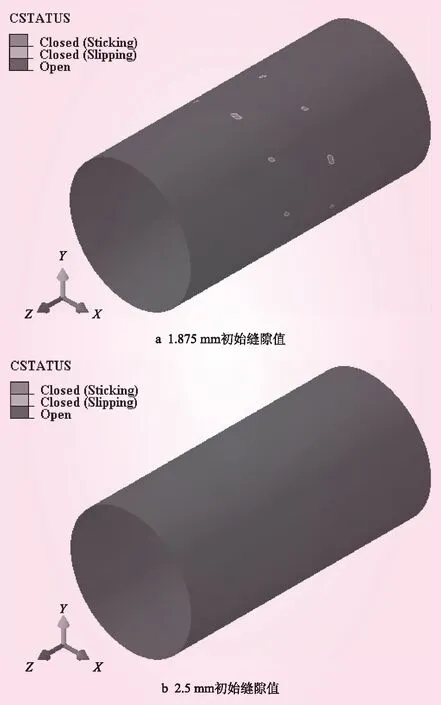
图7 不同初始缝隙值下钢管与回填混凝土的接触状态

由表2可知，初始缝隙值从0增大至1.875 mm时，钢管的屈曲临界压力逐渐降低。这是因为随着初始缝隙值的增大，钢管与回填混凝土的接触范围减小，回填混凝土对管壁变形的约束作用减弱，钢管的临界压力将会降低。但当初始缝隙值达到2.5 mm(相当于钢管半径的10/万)后，加劲环式地下埋管的临界压力保持不变，并与带加劲环明管方案的临界压力相同。这是因为在初始缝隙值达2.5 mm后，钢管在发生屈曲失稳时的外凸最大变形只有1.94 mm，小于初始缝隙值。结合图7可知，此条件下钢管与回填混凝土并未接触，回填混凝土将不会对钢管产生约束作用，因此该条件下加劲环式地下埋管方案的屈曲失稳与带加劲环的明管方案基本相同，加劲环式地下埋管在该初始缝隙值范围内的屈曲临界压力相同。

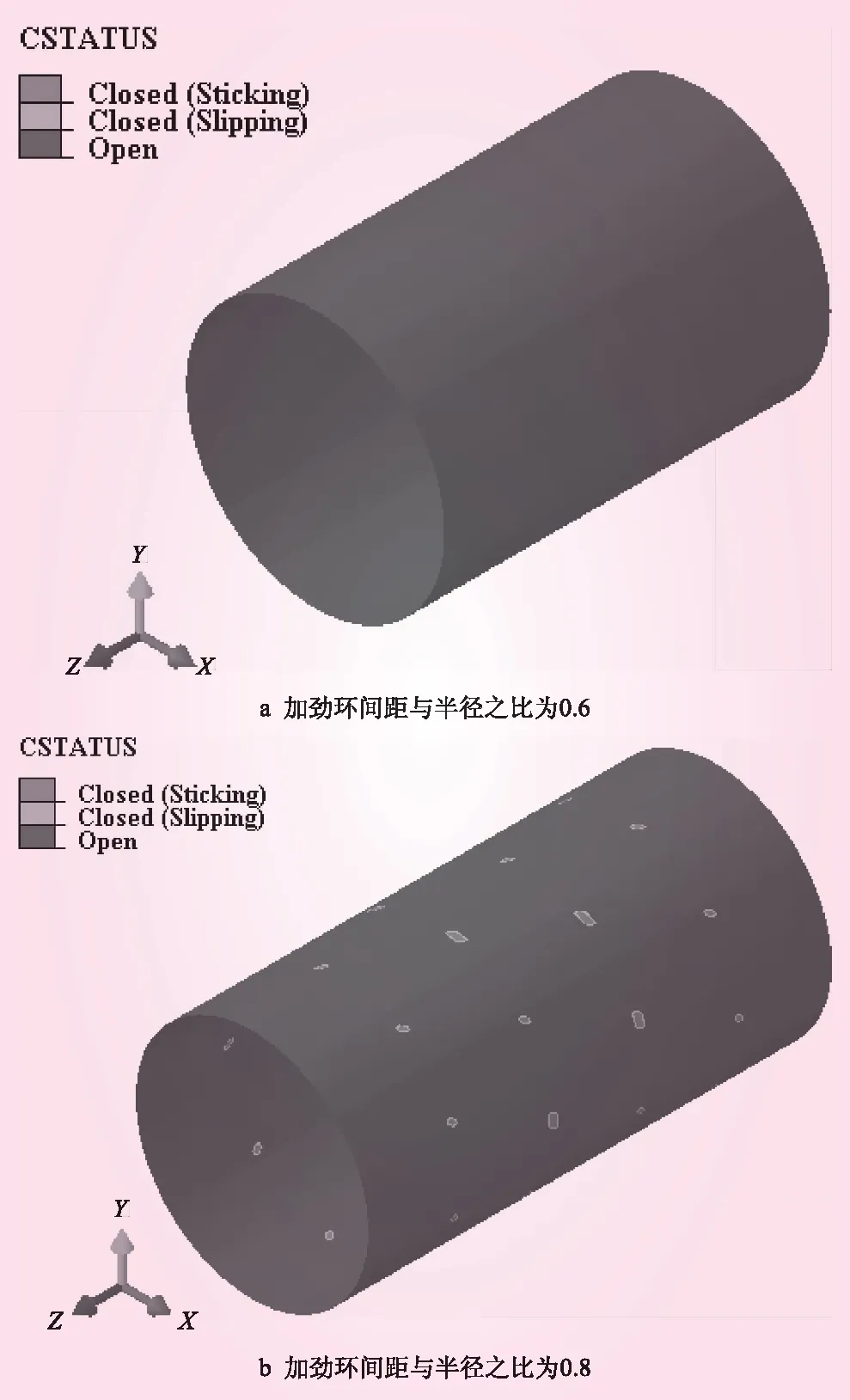
图8 不同加劲环间距下钢管与回填混凝土的接触状态

3.3 加劲环间距

在初始缺陷幅值取0.24 mm和初始缝隙值取1.25 mm的基础上，针对不同的加劲环间距对加劲环式地下埋管进行非线性屈曲分析，以研究加劲环间距对加劲环式地下埋管临界压力的影响。

当加劲环间距与半径之比小于0.6时，钢管发生屈曲失稳时与回填混凝土并未发生接触，如图8a所示，因此回填混凝土对钢管的变形将不会起到约束作用；随着加劲环间距的增大，钢管的整体刚度降低，钢管的屈曲临界压力会明显降低，当加劲环间距与半径之比大于0.8时，钢管与回填混凝土发生接触，如图8b所示，回填混凝土将会对钢管的变形产生约束作用。当加劲环间距与半径之比在0.8～1.2之间时，虽然加劲环间距增大使得钢管整体刚度减小，但由于受到回填混凝土较强的约束作用，钢管的临界压力降低不明显。随加劲环间距的进一步增加，加劲环对其间管壁的约束不断下降，回填混凝土对管壁变形的约束作用不足以阻止临界压力的下降，不同加劲环间距下加劲环式地下埋管临界压力见表3。

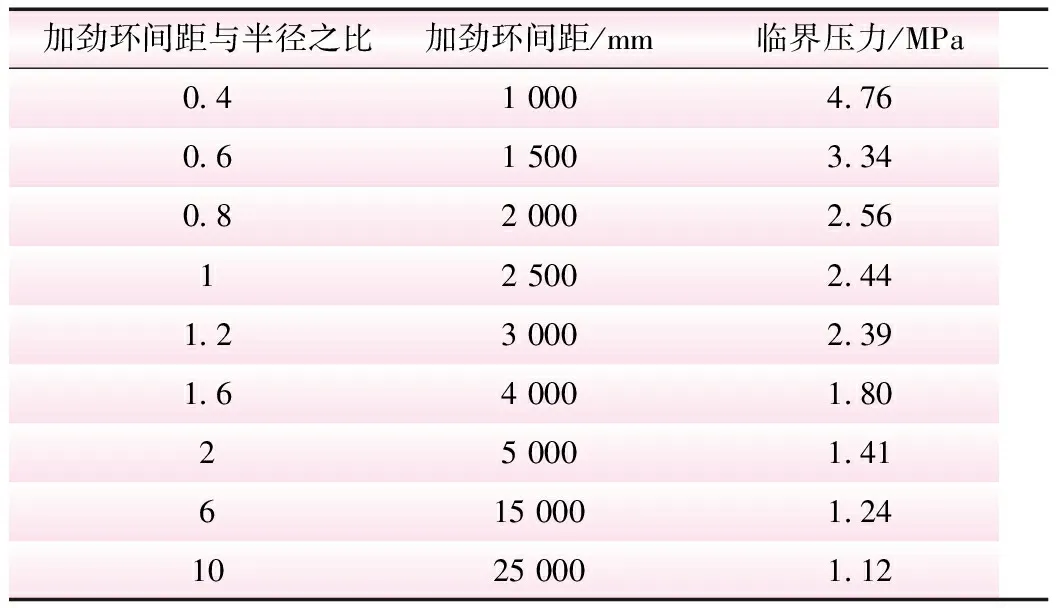
表3 不同加劲环间距下加劲环式地下埋管临界压力

3.4 加劲环高度

在初始缺陷幅值取0.24 mm、初始缝隙值取1.25 mm和加劲环间距取2 000 mm的基础上，针对不同的加劲环高度对加劲环式地下埋管进行非线性屈曲分析，计算结果如表4所示。从表4可知，随着加劲环高度的增加，钢管的屈曲临界压力有逐渐提高的趋势，但钢管屈曲临界压力的提高程度随加劲环高度的增加逐渐减弱，在加劲环高度达250 mm后临界压力基本保持不变。

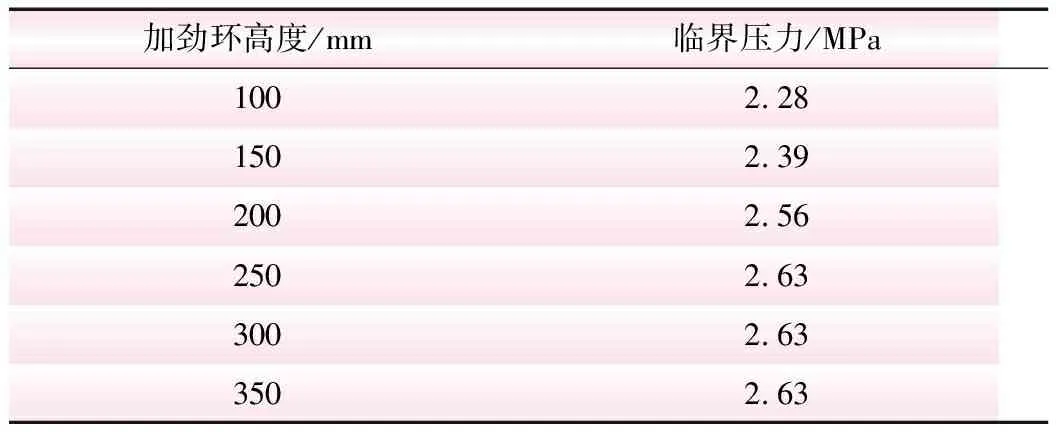
表4 不同加劲环高度下加劲环式地下埋管临界压力

4 解析法与有限元法临界压力的比较

选取加劲环间距为1 000、1 500、2 000、2 500、3 000、4 000、5 000 mm等7种方案，采用解析法及有限元方法对加劲环式地下埋管的临界压力进行计算。结果见图9。

由图9a可知，随着加劲环间距的增大，Mises公式和有限元法计算所得的管壁临界压力均逐渐减小。在加劲环间距小于1 500 mm时，通过Mises公式计算的管壁临界压力大于有限元法，这是因为当加劲环间距较小时，加劲环刚度对管壁的影响较大，而Mises公式认为加劲环为刚性环，这使得管壁的抗外压稳定能力偏高。在大多数加劲环间距范围内，Mises公式的计算结果均比有限元法小，这是因为Mises公式没有考虑钢管外回填混凝土对管壁变形的约束作用，计算所得的管壁临界压力偏小。

由图9b可知，随着加劲环间距的增大，各计算方法下加劲环的临界压力均逐渐减小，但有限元法得到的临界压力普遍高于各解析法。对于4种常用的解析法，Svoisky没有考虑加劲环承担等效翼缘以外管壁失稳可能传来的外压力，其计算所得的临界压力最高；Jacobsen法和Amstutz法假定加劲环之间的所有外压力由加劲环和等效翼缘以内的管壁承担，计算所得的临界压力居中；规范强度公式认为加劲环整个有效截面的环向应力达到钢材的屈服强度时发生失稳，其计算得到的加劲环临界压力最小。

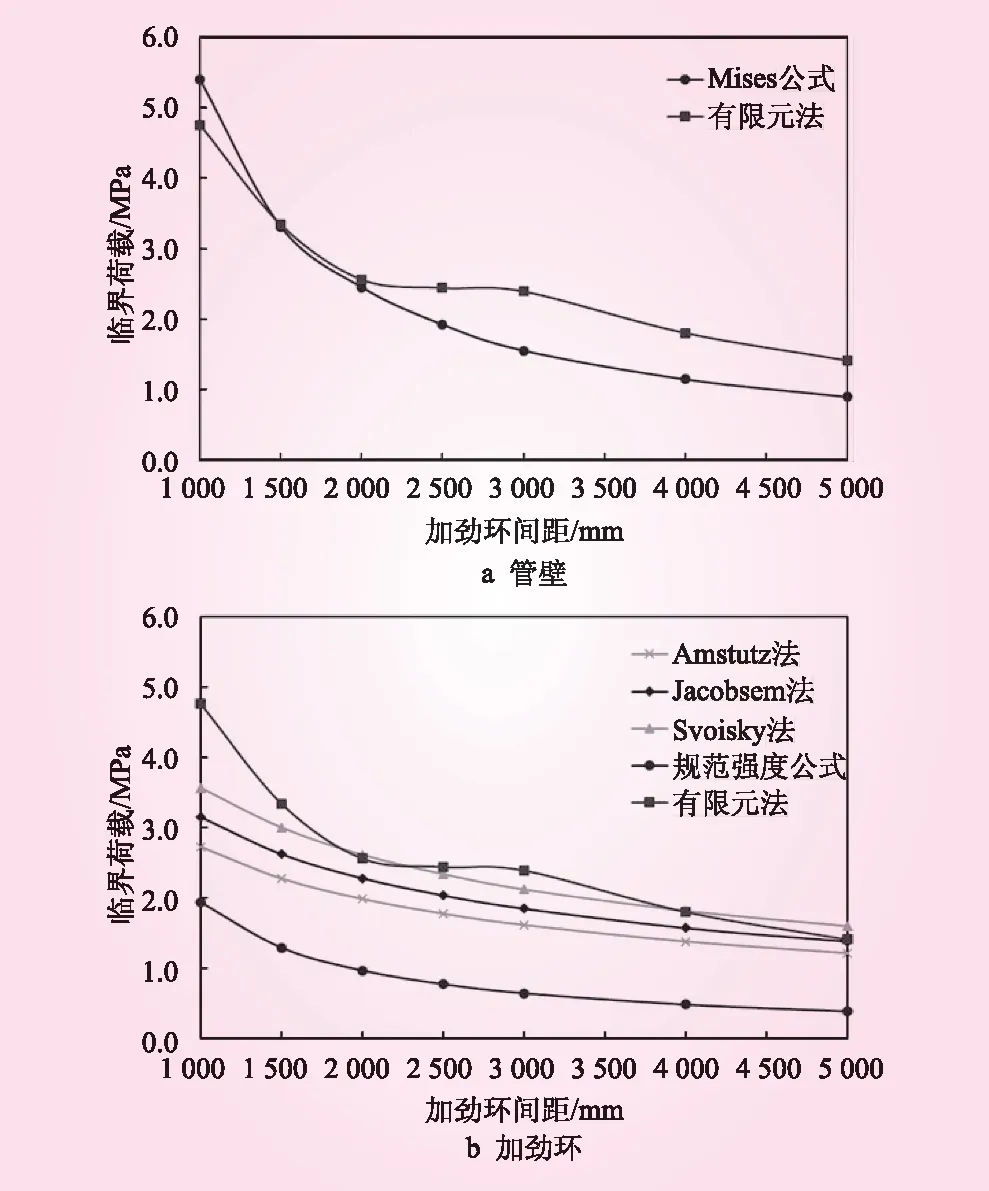
图9 解析法与有限元法临界压力比较

5 结 论

通过建立加劲环式地下埋管的有限元模型并对其进行有限元屈曲分析，进一步研究了钢管初始缺陷、初始缝隙值、加劲环间距和加劲环高度对加劲环式地下埋管临界压力的影响，最后将有限元法和常用解析法的计算结果进行对比，得到以下两点结论。

(1)对于加劲环式地下埋管，与带加劲环明管相比，考虑回填混凝土的约束作用后加劲环间管壁屈曲临界压力有所提高。各因素对临界压力的影响规律如下：随着钢管初始缺陷和缝隙值的增加，其临界压力基本呈下降趋势，但当初始缝隙值增大至钢管半径的10/万后，钢管临界压力与无回填混凝土的明管方案相同。当加劲环间距与半径之比小于0.8时，加劲环间距对钢管临界压力影响显著，之后随加劲环间距的加大而逐渐降低。加劲环高度的增加可以提高钢管临界压力，但在加劲环高度达到250 mm后临界压力基本保持不变。

(2)地下埋管抗外压稳定分析时，解析法对加劲环间管壁和加劲环自身的临界压力是分开计算的，而有限元法将管壁与加劲环作为一个整体来进行屈曲分析，与工程实际情况更相符。通过地下埋管有限元屈曲分析可以发现，加劲环在管壁屈曲失稳后才可能发生失稳，因此可不必单独校核加劲环自身的抗外压稳定。地下埋管的抗外压稳定设计思路可转变为：首先根据强度设计确定的管壁厚度按埋藏式光面管计算钢管的临界压力，若不满足抗外压稳定要求，则考虑设置加劲环；加劲环尺寸直接根据施工安装要求确定，再由解析法或有限元法计算加劲环间管壁的临界压力，从而确定加劲环的间距。