低轨道遥感相机光机热一体化分析及优化设计
2022-06-22刘朋朋靳利锋李妥妥
刘朋朋,靳利锋,赵 慧,李妥妥
(北京空间机电研究所 先进光学遥感技术北京市重点实验室,北京 100094)
0 引言
卫星在低轨道运行将遭遇特有的中性大气环境,太阳光投射角度的不同造成了大气具有季节变化、地方时变化以及随纬度的变化,卫星内部的热平衡决定于低轨道上的太阳辐射、地球和大气对太阳辐射的反射、地球大气本身的辐射及卫星本身的热辐射[1]。低轨道卫星受地球红外和地球反照外热流影响相比常规轨道比重更大,相机入光口外热流变化剧烈,相机阴影区和受晒区交替出现,热环境复杂恶劣。外热流动态变化时,相机系统结构中的成像光学器件的光学、结构等参数会受到温度效应的影响而发生改变,进而影响到系统的成像质量。为消除该温度效应的影响,可以采用一定的消热技术手段来实现[2]。无热化设计则是通过采用相应的技术(机械被动式、光学被动式、混合被动式等)使得光学系统在一定较大的温度变化范围内仍保持稳定的像面位置和质量[3-4]。
无热化设计时,需要从系统的、有机整体的视角综合考虑光、机、热等各分系统的设计参数的相互制约。目前,光机热一体化仿真分析方法作为国际上普遍采用的一种处理方法,其以多种专业的计算机辅助设计和分析工具(CAD/CAE 等技术手段)为基础,对影响空间光学系统精度可能面临的主要因素进行了全面充分的考虑,使系统光、机、热各方面之间的相互关系得以统一连贯地处理[5]。
美国国家宇航局Langley 研究中心率先采用了光机热集成分析技术,研制了一系列如10 m Keck 光学探测器、“哈勃”太空望远镜等多种空间光学遥感器[6]。国内傅丹鹰[7-8]分析了空间相机光机结构的导热特性,并运用热/结构、光学分析方法建立了空间相机分析模型,计算了由于热值刚体问题而产生的光学性能变化。赵振明[9]将某空间遥感相机在热平衡试验中不同位置测量得到的温度数据作为初始条件,完成了相机结构主体的热-机-光学集成分析,依次实施了相机温度场反演、热变形分析、光学系统性能分析,以及集成分析结果同试验测试结果的对比。单宝忠[10]采用Zernike 多项式作为有限元结构分析模型和光学分析模型之间数据传递的接口,对空间相机进行了系统集成分析。吴明长[11]等以白光望远镜为例,计算出该望远镜在不同系统温度下的光机热一体化分析结果。
为了评估低轨道热环境载荷作用下卫星相机光学系统的光学性能是否符合指标要求,以及指导相机结构参数的优化设计,本文采用一种基于在轨温度场的光、机、热一体化仿真分析方法,分析了相机成像时间内MTF 的变化,并据此对相机结构提供了量化的参数设计依据。
1 基本原理
1.1 光机热一体化仿真分析
光机热一体化仿真分析的实施原理是:从热分析得到的温度场结果出发,进行结构的热弹性变形分析。通过上述分析结果,得出支撑结构的热形变造成的刚体位移和光学元件在相关参数作用下产生的应力形变,将得到的数据文件依次经过刚体位移分离、Zernike 拟合,再通过动态数据交换接口导入到光学分析专业工具软件(如Zemax、Code V 等)中,进而求解分析光学系统结构模型在热环境下的各项光学性能参数[10]。根据计算得到的光学性能参数以及结构分析和热分析的结果,可以指导结构设计、热设计要求,参考确定是否需要设计修正。
本文旨在解决光、机、热一体化仿真分析涉及到的热学、力学数据接口以及力学、光学数据接口的问题。对于热学和力学数据接口,需要将热分析得出的温度场施加到力学有限元分析软件(如Ansys、Nastran、Abaqus 等)中,分析不同温度分布时所引起的器件的结构变形即热变形。本文通过不同的软件架构实现热分析和力学分析,其中,通过Thermal Desktop 实现热分析,通过MSC Patran/Nastran 中实现力学分析,需要将热分析温度场进行插值转化到Patran/Nastran 中。对于力学和光学数据接口,温度载荷造成的结构形变响应导致光学器件的结构支撑产生刚体位移与刚体转动,这会改变光学系统中各个光学镜面之间的相对位置和相对方向;同时光学元件自身也会受热载荷而发生变形,从而对系统光学性能发生影响。本文对变形后的镜面有限元节点利用Sigfit 计算其刚体位移和刚体转动量,同时提取镜面的Zernike 多项式拟合系数,一并将刚体变形值与多项式系数拟合值输入至Code V 光学分析软件中,然后对变形后光学系统的性能进行评估。
1.2 Zernike 多项式拟合
光学元件镜面的变形分为刚体位移和表面畸变。刚体位移表现为拟合球面与原镜面之间的位移,包括平移、离轴和倾斜,可以通过调整镜子间距、偏转等方法消去,表面畸变表现为拟合球面与实际曲面之间的误差[2]。
光学镜面变形用Zernike 多项式进行拟合,可以提供一个紧凑精确的表达方式。Zernike 多项式在一个规范化的圆域上形成一个彼此正交的集合,该正交性条件允许Zernike 多项式中的每一项可以独立地从不同阶的多项式间加以分离,具有反变换和描述图像信息冗余度最少的特点。
某表面的Zernike 多项式数学描述:
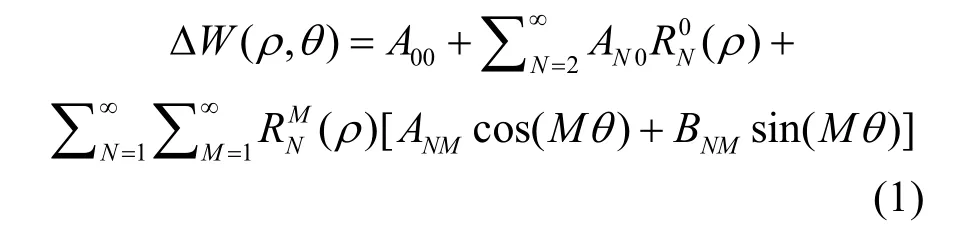
Zernike 多项式同时描述了波前像差,其中的各阶模式都有很明确的物理含义,与光学设计中的Seidel 像差系数相对应。如第一项常数项表示表面的偏移,第二、第三项表示表面沿两个正交平面的倾斜,第四项表示表面的离焦(表面形状在沿径向方向的抛物线形的改变量)等[12]。
因此Zernike 多项式便可以作为机械和光学软件工具之间集成和数据交换的一个有效载体。当前的光学设计分析软件(Zemax OpticStudio、Code V 等)均支持使用Zernike 多项式系数线性组合表示表面的变形,如Zemax OpticStudio 可使用Zernike 相位参数生成特定波长、特定视场下的像差数据。将光学镜面热变形的有限元位移值转换拟合成各阶Zernike 多项式系数后,便可以直接加载至不同的通用光学设计分析软件的光学模型中进行后续分析。
1.3 分析流程
光机热一体化仿真分析流程如图1所示,首先采用Creo 三维建模工具建立相机实体模型,在此基础上分别用Thermal Desktop、MSC Patran/Nastran、Code V 构建热分析模型、结构有限元分析模型,光学分析模型,3 个模型采用完全一致的坐标系定义,并保持单位制统一,热模型与结构有限元模型中各个部件的位置保证一致以提高温度场数据传递的准确性。由于相机在低轨道运行时太阳直射角和地球反照角度均随季节、昼夜时刻不同不断变化,由于工作模式的不同还需要进行姿态的变化,热分析模型需要考虑这些复杂工况下的极端外热流,同时考虑电子器件热耗以及主被动温控措施的共同作用,通过分析选取了相机单次成像时间内的最极端工况,计算温度场,然后将温度场映射于结构有限元模型进行热变形分析。
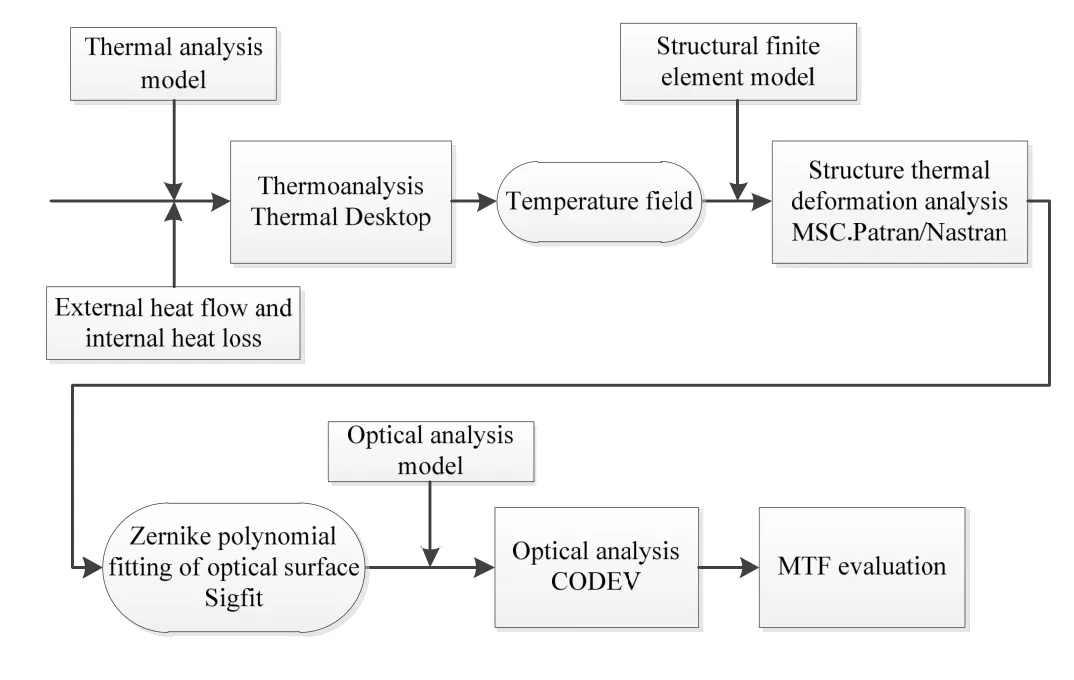
图1 光机热一体化仿真分析流程Fig.1 Analysis process of integrated opto-mechanical-thermal
结构有限元模型对相机光学元件、支撑结构等各部分结构详细构建并进行一定程度的简化。进行有限元分析,提取各反射镜镜面节点位置和位移数据,采用Sigfit 进行Zernike 多项式拟合,得到各反射镜镜面刚体位移和镜面面形,再代入光学分析模型,得到极端工况下相机系统MTF 变化情况。
2 光机热一体化仿真分析
2.1 光机热一体化分析模型的建立
本文以某低轨道遥感相机为例进行了分析,给出了相机成像时间内阳照区最极端工况(最低温工况以及最高温工况)的计算结果。该相机采用四反同轴光学系统,光学件采用了高比刚度、低热膨胀系数的材料,各个环节的支撑结构均考虑了消热设计,采取了相机与卫星之间解耦安装等多种高稳定性设计手段,并实施了高精度的主被动控温措施。
热分析模型中,各反射镜组件、主体支撑结构均按照设计真实状态建模,外热流按该工况下的极端外热流进行计算,相机与卫星之间简化为定温边界,内部热源进行了简化建模,相机热分析模型如图2所示。
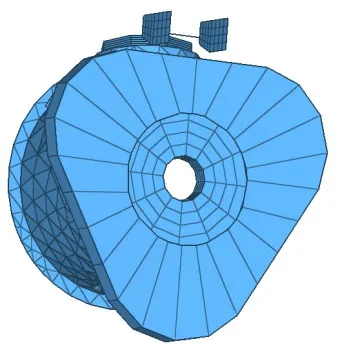
图2 相机热分析模型Fig.2 Thermal analysis model of the camera
结构有限元分析模型中,采用Altair Hypermesh对相机光学部件和主体结构等进行有限元网格划分,采用壳单元与实体单元结合的方式建模,其中相机主体及支撑结构采用四边形壳单元及四面体实体单元建模,反射镜、粘胶以及支撑镜框采用四面体单元、楔形体单元建模,其中反射镜与支撑结构间的胶层需要至少划分3 层网格以保证力矩的传递和镜面面形的计算精度。模型规模为438690 节点,1065230 单元,如图3所示。
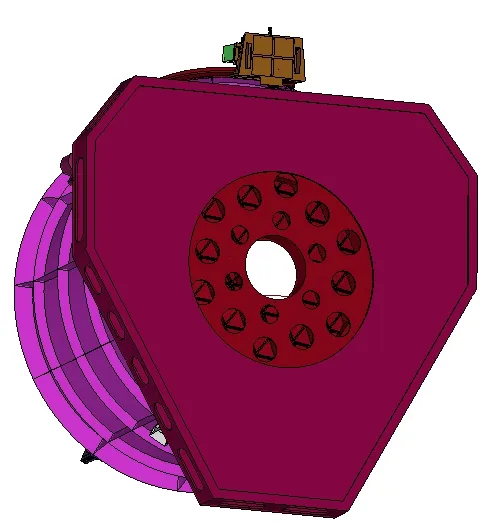
图3 相机结构分析有限元模型Fig.3 Structural analysis finite element model of the camera
结构分析有限元建模计算中相机各反射镜及结构支撑部件所赋予的材料及其属性参数如表l所示。
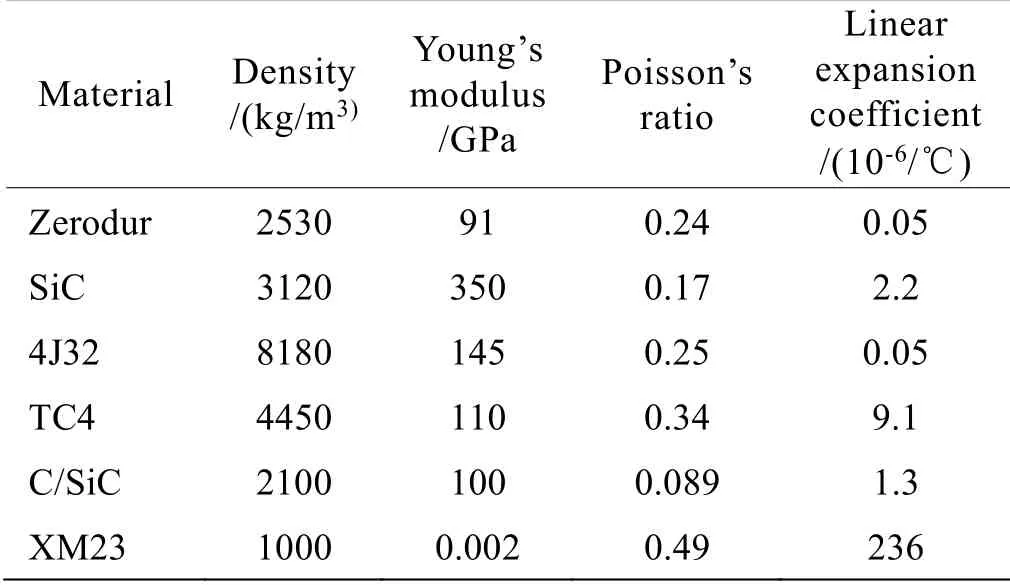
表1 相机反射镜及结构支撑材料属性Table 1 Materials and properties of mirror structural supports
在进行变形计算时,根据低轨道相机的实际安装状态确定约束条件为3 处安装底座。系统的温度载荷由热分析计算的温度场映射到结构有限元模型中得到,如图4所示。
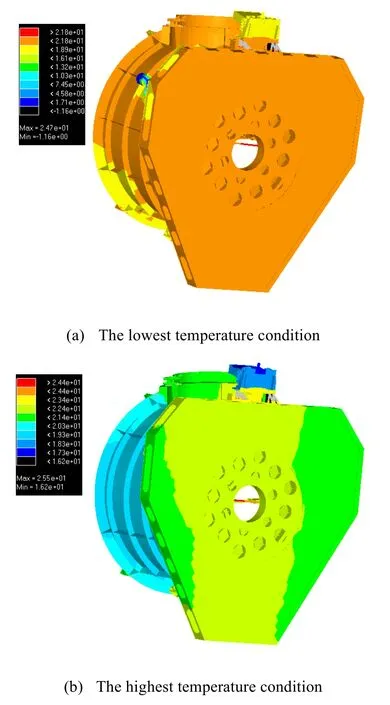
图4 相机温度场Fig.4 Camera temperature field
2.2 分析结果
将热网格温度场映射反演至结构网格的有限元模型,然后进行热变形分析,分别计算了反射镜的自身变形、相机结构支撑变形导致的光学反射镜元件的位置、方向变化及镜面面形结果,图5 给出了相机变形云图。将各光学反射镜表面的有限元节点坐标值及位移值在Patran 后处理中进行提取,并在Sigfit 中拟合计算镜面Zernike 多项式描述的各项系数。图6 及表2 给出了相机成像时间内阳照区最低温工况、最高温工况主镜镜面面形及拟合得到的前9 项Zernike多项式系数。
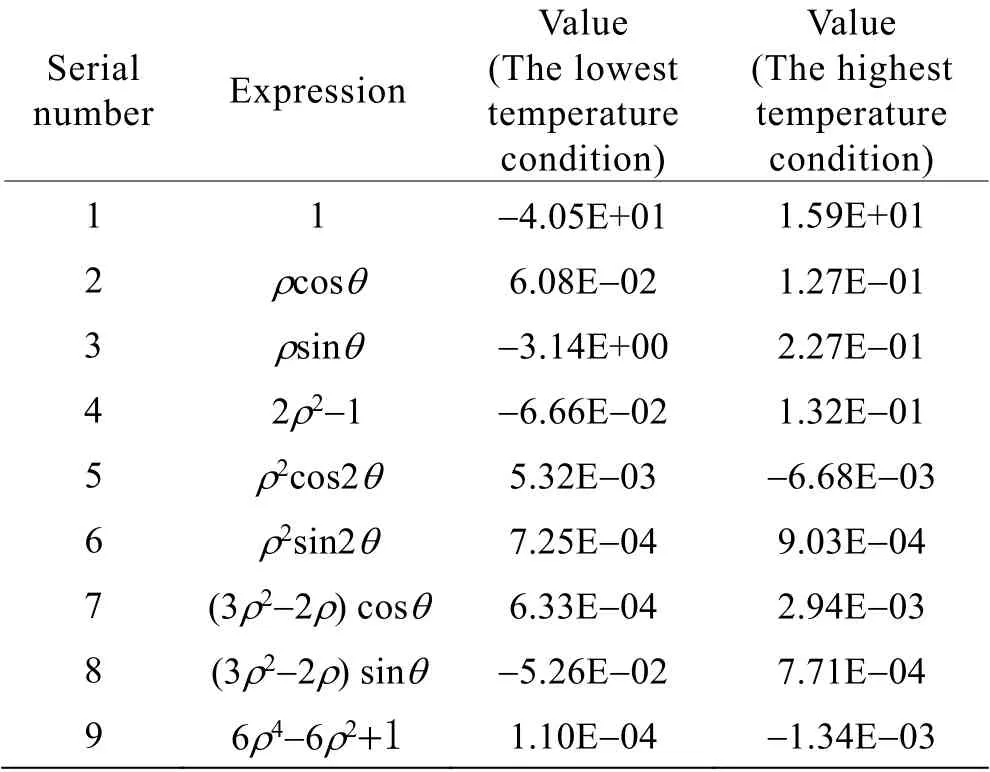
表2 主镜Zernike 系数Table 2 Zernike coefficient of primary mirror
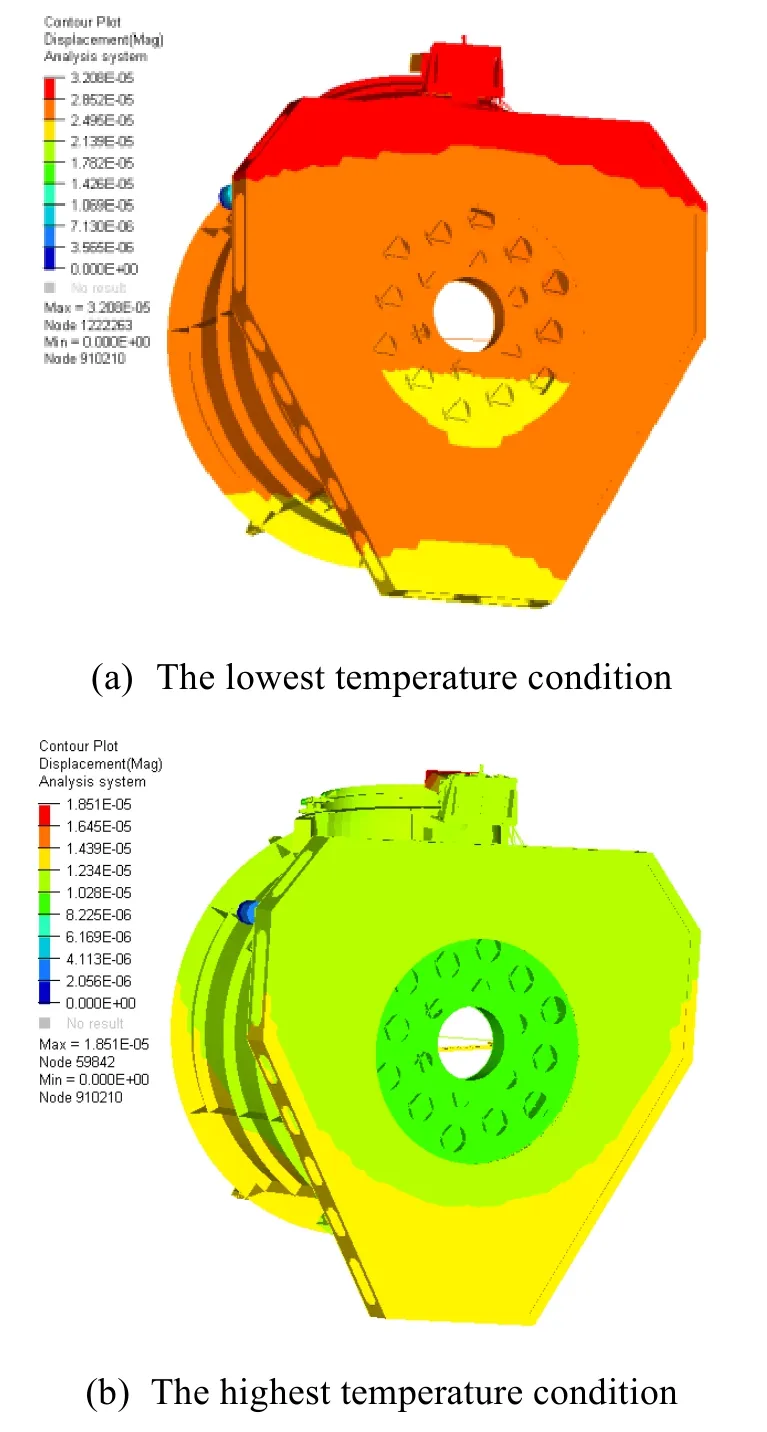
图5 相机结构热变形结果Fig.5 Thermal deformation results of the camera structure
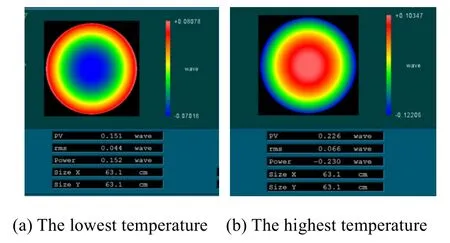
图6 主镜镜面面形Fig.6 Surface shape error of primary mirror
图7 和图8 分别给出了各反射镜在成像期间内由温度场变化引起的平移及倾斜位移变化量、镜间距变化量。其中,主镜和次镜光轴方向的位移(Z向位移)较大,主要原因是主镜安装在主承力板结构中心,主承力板在温度场作用下会发生向内的弯曲变形,导致主镜跟随移动;次镜安装在前镜筒上,前镜筒轴向跨度较大,在热胀的作用下变形较大。四镜和五镜Y向位移最大,其原因是四镜和五镜安装在前镜筒侧面,受不均匀温度场的作用而产生较大偏心位移。X向位于相机对称面内,相机温度场分布在对称面左右也近似对称,故各反射镜在该方向上的位移均接近于零。主次镜镜间距变化量亦最大,表明在主承力板和前镜筒支撑热变形的共同作用下对主次镜的影响是最大的。经过后续光学分析,各镜面的倾斜位移量对系统传函影响很小,可以忽略不计,并认为主次镜的轴向位移及镜间距变化是影响系统传函的主要因素。
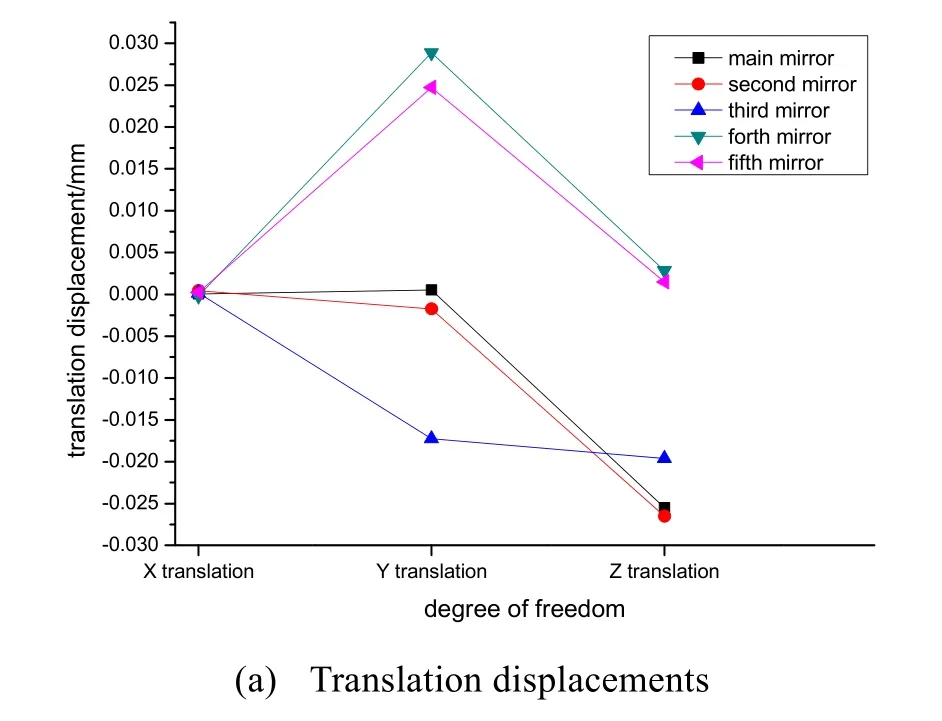
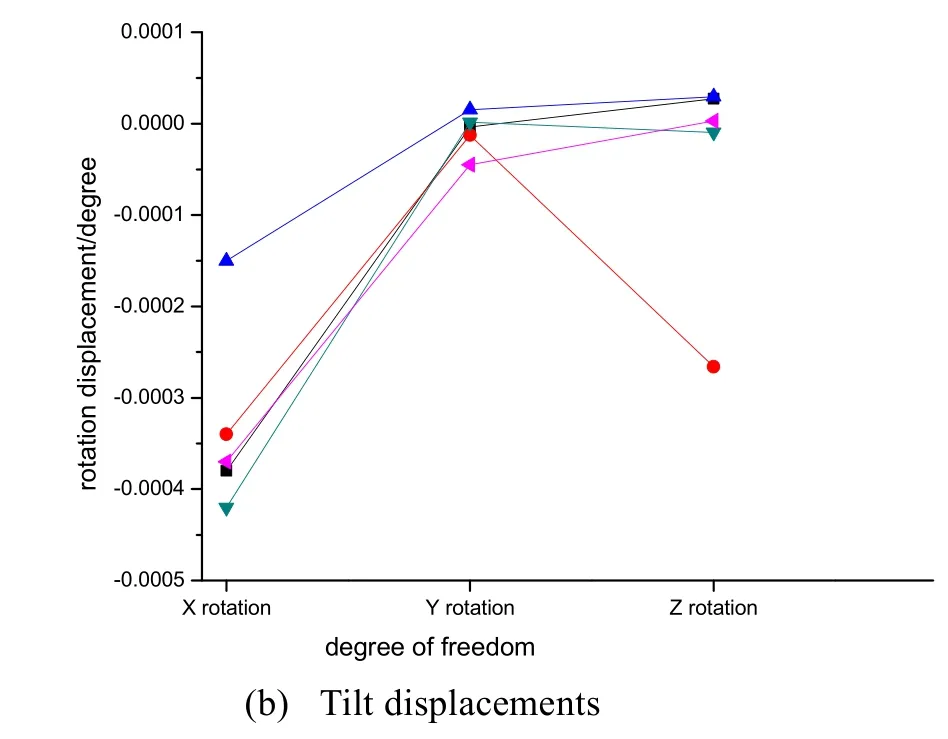
图7 各反射镜平移及倾斜位移Fig.7 Translation and tilt displacements of each mirror
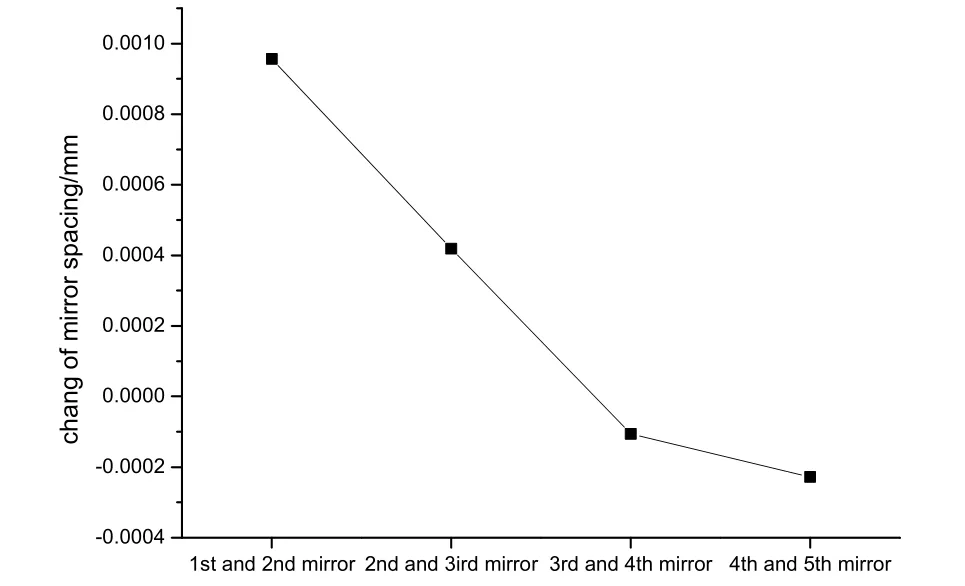
图8 各反射镜镜间距变化Fig.8 Variation of each mirror spacing
最后,将各反射镜的Zernike 系数导入光学分析模型,即可得到系统传函的变化。本相机系统传函指标要求达到0.3,图9 给出了系统传函在成像期间内阳照区最低温工况及最高温工况的变化情况,其中奈奎斯特频率(Nyquist frequency)处MTF 值分别为0.24 及0.18,已经小于指标要求,该工况下相机成像质量不满足使用需求,需要通过改进结构热特性,进行结构参数的优化设计。
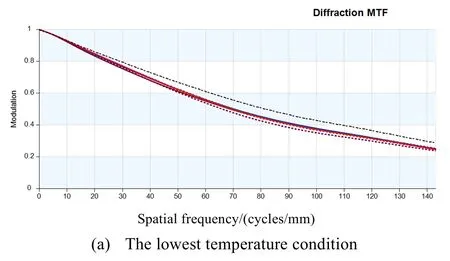
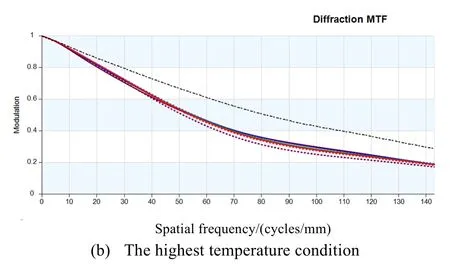
图9 系统传函变化Fig.9 Variation of system transfer fuction
2.3 优化设计
从分析结果看,主、次镜成像期间内的温度变化已经确定,反射镜部件本身在温度载荷作用下的结构变形由镜体材料决定,而主次镜间距受主承力板和前镜筒热特性的共同作用,故不改变反射镜部件自身的结构特性,从主承力板和前镜筒等支撑结构的结构参数出发进行优化设计。
从前述分析来看,主镜轴向位移影响最大,通过改变主承力板的线胀系数,可以改变其向内的弯曲变形程度,进而改变主镜轴向位移。为了将问题进行简化,便于控制变量,对相机结构进行均匀温升分析。保持其他参数不变,在1~9×10-6范围内由小到大不断调整主承力板线胀系数,进而优化主次镜间距,改善系统成像特性。
图10 给出了不同主承力板线胀系数下相机均匀温升结构变形图,图11 给出了主次镜间距随主承力板线胀系数的变化曲线。图中可以看出,随着线胀系数的增加,主承力板的结构变形呈现由向光轴方向凸出到平面内膨胀,再到向光轴方向凹进的变化趋势。主次镜间距变化量呈现先减小后增加的趋势,与结构变形趋势是一致的。并得出主承力板线胀系数在(5~5.5)×10-6时,主次镜间距基本没有变化,系统热特性达到最优。

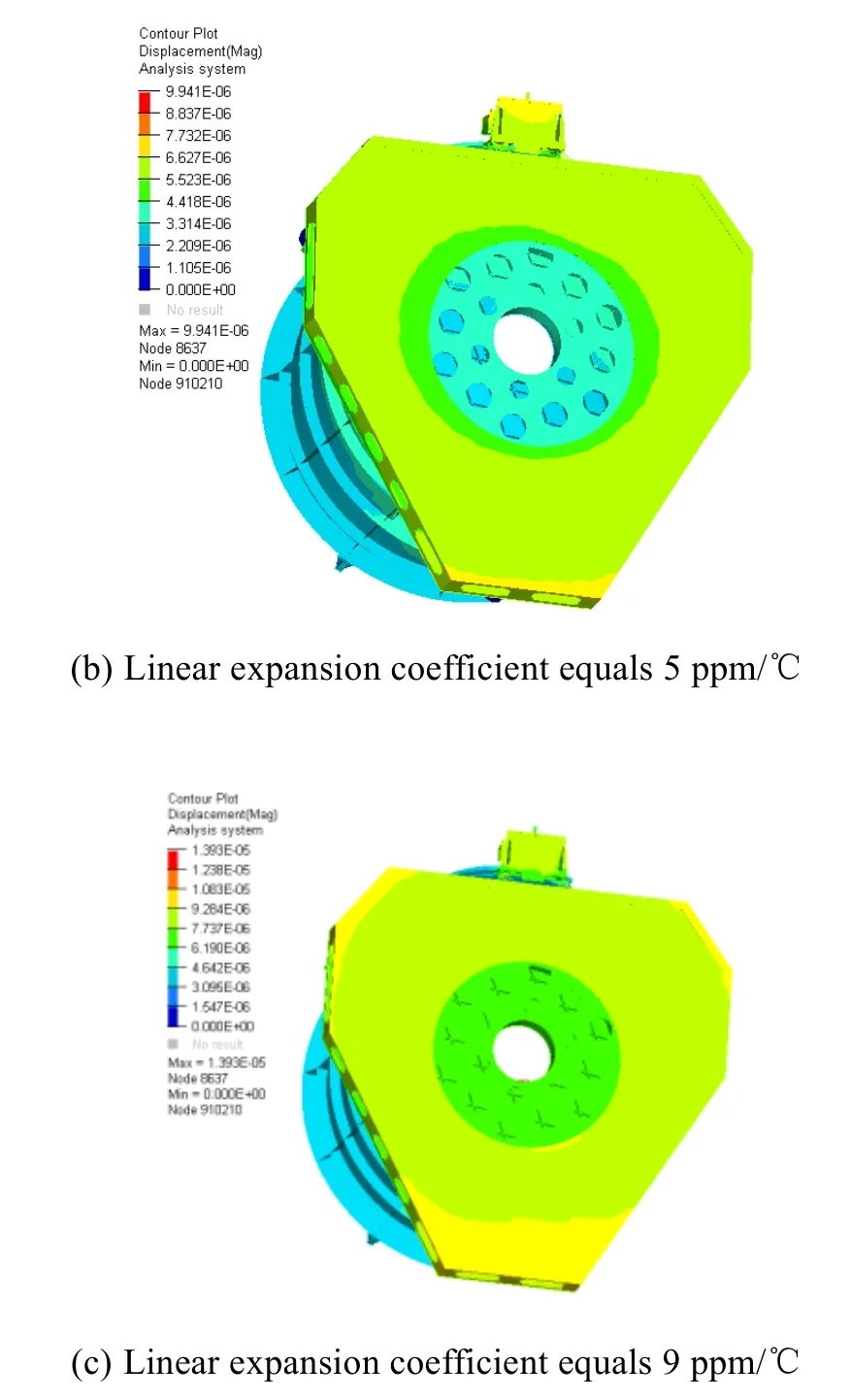
图10 均匀温升相机结构变形Fig.10 Structure deformation by uniform temperature rising
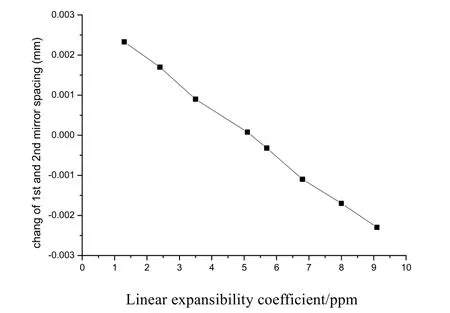
图11 不同主承力线胀系数主次镜间距变化Fig.11 Variation of primary and secondary mirror spacing with different linear expansion coefficients of the principle bearing
图12 给出了主承力板结构参数优化后系统传函在成像期间内阳照区最低温工况及最高温工况的变化曲线,可以看出经过结构参数的调整优化系统传函已经达到指标要求,在外热流和相机温控措施作用的成像时间内最极端工况下,相机成像质量满足使用需求。
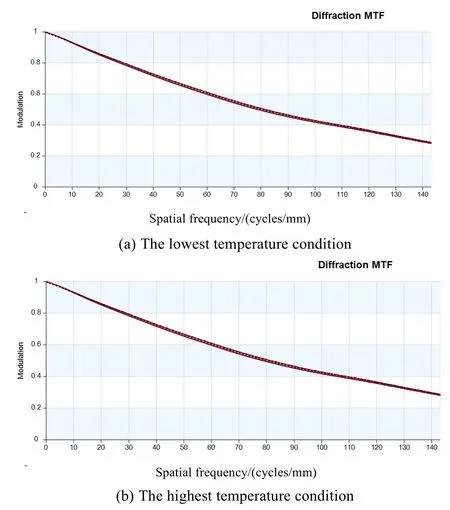
图12 优化后最低温、最高温工况系统传函变化Fig.12 Variation of system transfer fuction after optimization
2.4 在轨微振动光机一体化分析
遥感相机在轨期间还会经受卫星CMG 执行机构、动量轮等微振动源的影响。对此微振动的评估可采用本文的光机一体化分析方法。在相机安装点处施加CMG 微振动扰动力和力矩的时域数据,使用Patran/Nastran 进行时域瞬态响应分析,结构阻尼按照一般经验取临界值0.005。分析得到各光学反射镜面6 个自由度的位移响应,再进行Zernike 多项式拟合代入光学分析模型采用光线追迹法计算1 s 内中心视场的像移变化,结果如图13所示。
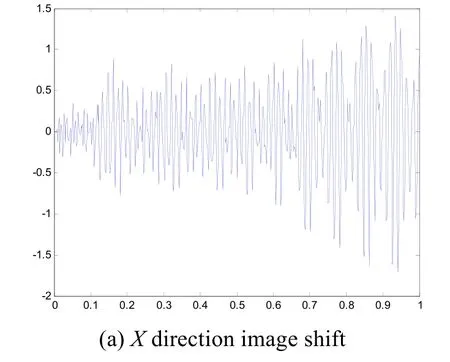
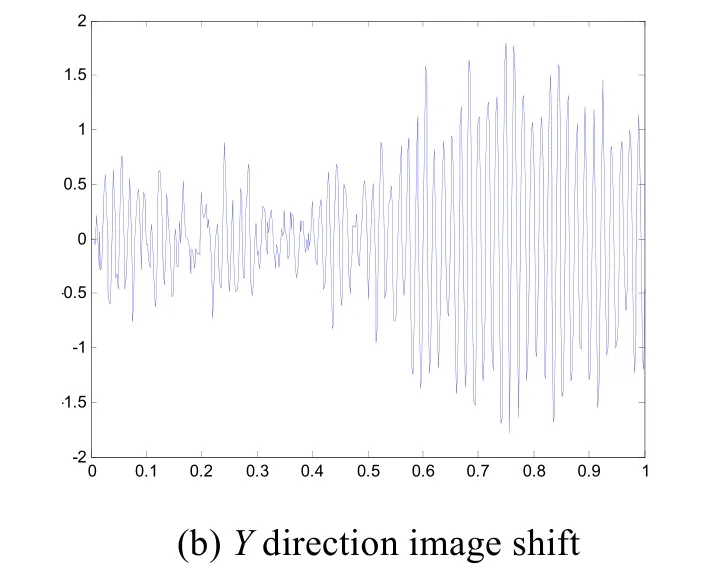
图13 中心视场像移变化Fig.13 Image shift variation of central view field
分析结果表明,中心视场像点最大X向位移为1.43 μm,最大Y向位移为1.83 μm。最大像移小于0.3个像元,满足相机系统成像质量要求。
3 总结
本文以极端热环境载荷作用下低轨道卫星相机为研究对象,提出了一种基于在轨温度场的光、机、热一体化仿真分析方法,解决了低轨道相机光学系统热性能的验证问题,分析实例证明了该分析方法的有效性。通过一体化仿真分析,计算了极端工况下相机系统传函,剖析了其结构参数的影响因素。在此基础上进行了主承力结构参数的优化设计,最终相机成像指标得到了满足。该分析方法可以在研制初期指导改进相机设计,极大地缩短研制周期,同时对地面试验相机系统性能进行预估。
