基于相位和表面温度的缺陷定量识别及其对比研究

陈 林，黎敏谦，高 峰，刘 敏，张 弛

（1.海军士官学校兵器系，安徽 蚌埠 233000；2.海军92957 部队，浙江 舟山 316000）

0 引言

红外检测作为一种新型无损检测技术，具有快速、直观等优点，其常见的检测方法有：脉冲检测法、锁相检测法和脉冲相位检测法[1-3]。其中，脉冲检测法是基于表面温度的检测方法，锁相检测法和脉冲相位检测法是基于相位的检测方法，作为新型检测技术，正得到广泛的研究和应用。例如，文献[4-5]利用脉冲检测法对复合材料的内部缺陷检测进行了研究；文献[6-7]采用脉冲检测技术对固体火箭发动机绝热层的脱粘缺陷检测进行了研究；文献[8-10]采用锁相检测技术分别对碳纤维夹层结构、平底钢材料和囊体布的缺陷检测进行了研究；文献[11-12]对提高脉冲相位检测法的检测效果和效率进行了研究。文献[4-12]在进行红外检测的研究时，被检测材料缺陷的大小，主要是通过对其红外图像的处理得到，而每种红外图像处理算法都有局限性；对于缺陷深度的确定，主要是通过构建缺陷深度与检测表面的温度差或者相位差间的拟合关系来实现的，但是检测表面的温度差或者相位差的大小不仅会受到缺陷深度的影响，还会受到缺陷大小的影响，因而在确定缺陷深度与检测表面的温度差或者相位差间的拟合关系时，需要在相同的缺陷大小下进行。但是，实际检测时，不可能准确地识别缺陷的大小，会存在一定偏差，因此，为了提高缺陷深度的检测精度，构建的拟合关系往往需要根据经验添加一个修正系数，而修正系数会受材料特性的影响，对于不同材料需要通过相应的实验来确定，增加了缺陷定量检测的复杂度，并且在实际检测时，往往会因修正系数的不准确而带来较大的检测误差。为了提高红外检测的精度，本文将共轭梯度算法与脉冲相位法和脉冲检测法相结合，实现了对缺陷深度和大小的同步检测，并通过数字算例对检测方法进行了验证，比较了两种检测方法的优缺点，为促进缺陷定量检测的发展提供了一定的理论指导。

1 正问题模型

本文研究的是二维导热下的识别问题，如图1所示，试件内部含有矩形缺陷，缺陷内充满空气，试件大小为L1＝80 mm、L2＝20 mm，缺陷的位置大小通过参数Lx1、Lx2、Ly1、Ly2来确定（参数Ly2决定了缺陷的深度，参数Lx1、Lx2决定了缺陷的宽度大小，参数Ly1、Ly2决定了缺陷的高度大小），qs为加载到表面的热流强度。

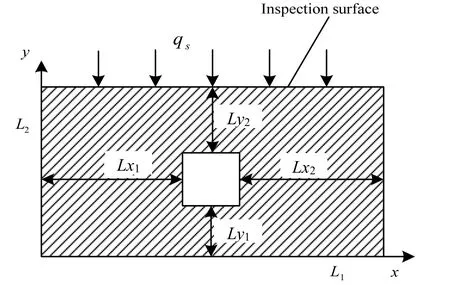
图1 二维热传导模型Fig.1 The model of two-dimensional heat conduction

二维试件的导热微分方程可写为：

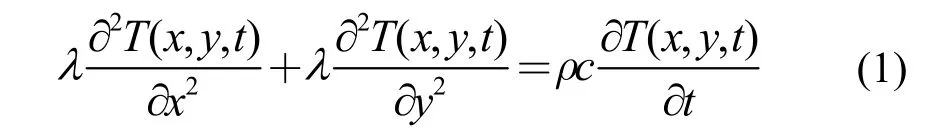
初始条件：

边界条件：

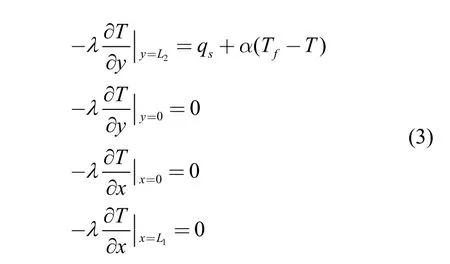
式中：λ为导热系数，W/(m·℃)；T为温度，℃；c为比热容，J/(kg·℃)；ρ为密度，kg/m3；qs为热流强度，在t＝0～0.1 s，qs＝2×107W/m2，在t＞0.1 s 时，qs＝0；α＝10 W/m2为换热系数；Tf＝20℃为环境温度。试件及其内部空气的物性参数如表1所示。正问题求解是为了得到检测外表面的温度分布和相位分布信息，从而为反问题的求解提供依据。

表1 材料的物性参数Table 1 Thermal properties of materials

2 反演识别求解过程

2.1 共轭梯度算法

共轭梯度算法（conjugate gradient method,CGM）通过使目标函数S(P)达到极小化来确定识别结果，即S(P)＜ε（ε为给定的极小正数）。

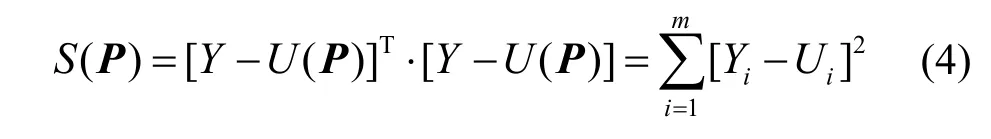
式中：P＝(p1,p2,p3,…,pn)是待识别的参数向量，对于本文P＝(Lx1,Lx2,Ly1,Ly2)；m为x方向上的离散网格数；Yi为实际测量得到的值；Ui为在参数向量P下通过公式(1)～(3)计算得到的理论值（基于表面温度检测时，Yi、Ui为表面温度值；基于相位检测时，Yi、Ui为相位值）。

2.2 共轭梯度算法的迭代原理

共轭梯度反演识别算法的迭代公式为：

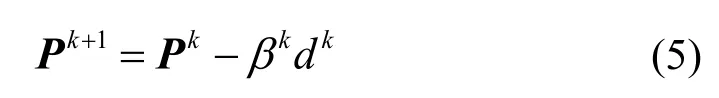
式中：Pk为第k次迭代的结果；dk、βk分别为第k次迭代的共轭搜索方向和搜索步长，其计算公式为：

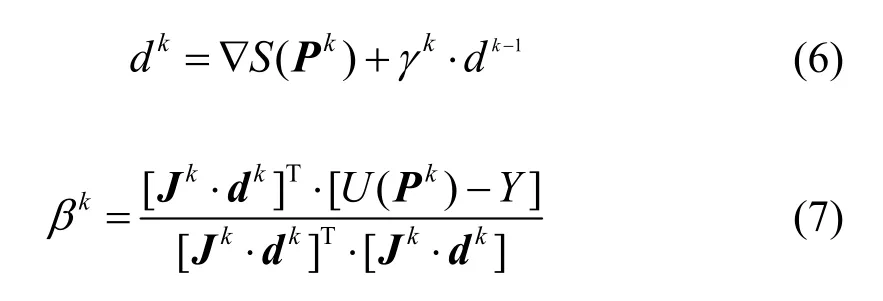
式中：∇S(Pk)为共轭梯度方向；γk为共轭系数；Jk为敏感系数矩阵；其表达式分别为：

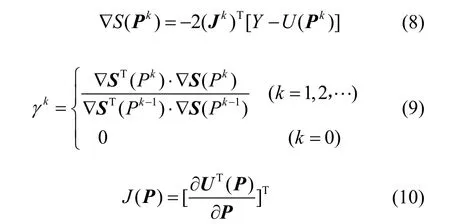
2.3 迭代求解过程

对于本文缺陷的识别问题，其识别过程可描述为：通过共轭梯度算法不断修正缺陷参数Lx1、Lx2、Ly1、Ly2的初始假设值，以期找到一组Lx1、Lx2、Ly1、Ly2值，使得在此组Lx1、Lx2、Ly1、Ly2值下通过公式(1)～(3)计算得到的理论值与实测值相吻合（基于表面温度检测时，理论值与实测值为表面温度；基于相位检测时，为相位），求解流程如图2所示。

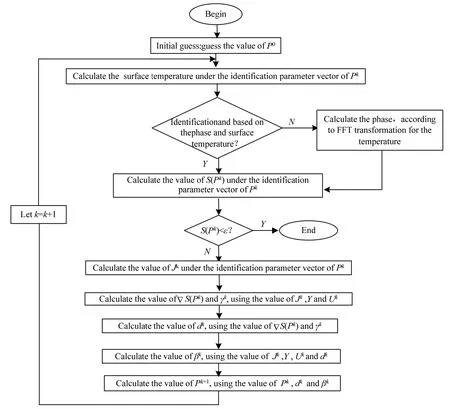
图2 基于相位和表面温度的CGM 反演识别算法流程图Fig.2 The flow chart of CGM inversion algorithm based on phase and surface temperature

3 算例及其分析

在进行定量识别的数字验证过程中，首先假定一组Lx1、Lx2、Ly1、Ly2值，通过方程(1)～(3)计算得到表面的真实温度值，然后依据公式(11)提出的测温误差模拟方法，将测温误差添加到由方程(1)～(2)计算得到的理论温度值上，以此作为实际检测时表面的温度值，对温度进行FFT 变换，得到检测表面的相位，然后再假设一组Lx1、Lx2、Ly1、Ly2的初始值，以表面温度或者相位为依据，利用共轭梯度法迭代求解出Lx1、Lx2、Ly1、Ly2的最终值。

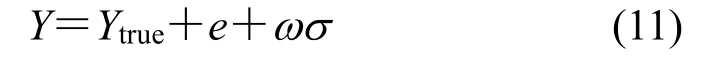
式中：Y为实测温度；Ytrue为真实温度；e为均匀误差；ω为随机数（－1.0～1.0），σ为偏差程度。

为了评价识别的准确性，定义识别结果的相对误差：

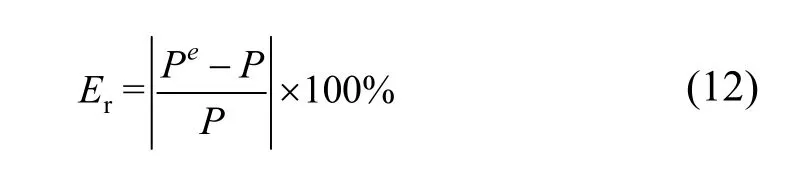
式中：Er为相对误差；Pe为识别结果；P为真实值。

表2 为不考虑测温误差时在不同初始假设下的识别结果（材料内部缺陷的真实值为Lx1＝35 mm、Lx2＝25 mm、Ly1＝10 mm、Ly2＝5 mm。）。由表2 可以看出，当不存在测温误差时，在不同的初始假设下，基于相位和表面温度的识别方法都能准确地识别缺陷位置大小。

表3 为不同随机误差下的识别结果，材料内部缺陷的真实参数值为Lx1＝35 mm、Lx2＝25 mm、Ly1＝10 mm、Ly2＝5 mm，初始假设为Lx1＝15 mm、Lx2＝35 mm、Ly1＝5 mm、Ly2＝10 mm。从表中可以看出，当测温误差较小时，基于相位和表面温度的识别结果都有较高的精度，但当随机误差增大时，识别结果的精度都会降低，可见基于相位和表面温度的识别精度都对随机误差敏感，识别精度会随着随机误差的增大而降低。

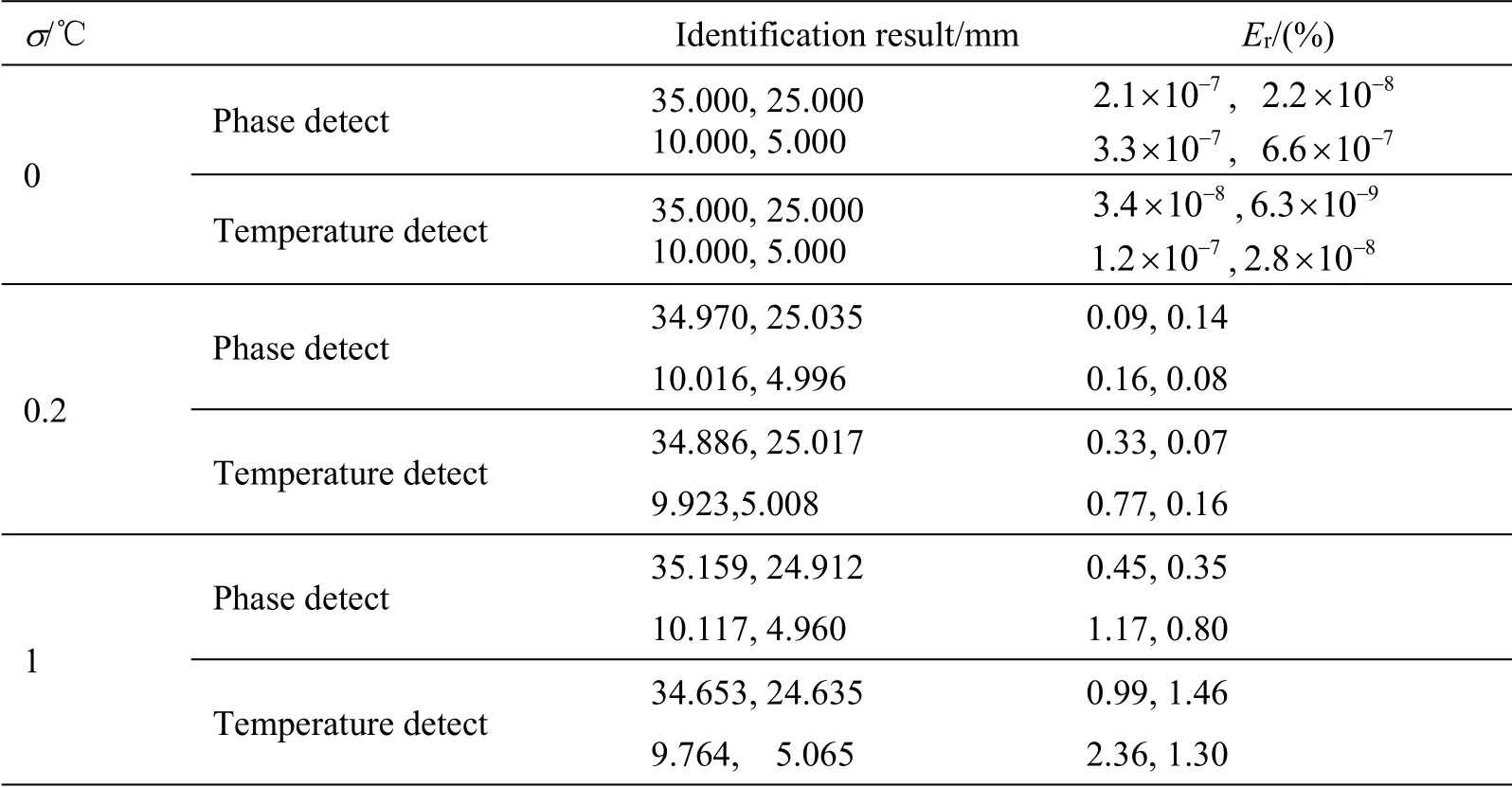
表3 不同随机误差下的识别结果Table 3 Results in distinct random temperature errors

在实际测温时，如果选取的发射率与物体表面的发射率存在偏差，或者背景辐射较复杂时，会导致测得的温度值与被测物体的实际温度间出现均匀误差[13-14]。表4 为不同的均匀误差下的识别结果，材料内部缺陷的真实参数值为Lx1＝35 mm、Lx2＝25 mm、Ly1＝10 mm、Ly2＝5 mm，初始假设为Lx1＝15 mm、Lx2＝35 mm、Ly1＝5 mm、Ly2＝10 mm。由表4 可以看出，基于相位的识别都能准确地识别出材料内部缺陷的位置，识别结果精度不随均匀误差的增大而增大；而基于表面温度的识别在均匀误差较小时有较好的识别精度，随均匀误差的增大识别精度将降低，特别是参数Ly1的识别精度较差。可见均匀误差对基于相位的识别无影响，而对基于表面温度的识别影响较大。因此，在实际检测时，如果采用基于表面温度的检测，应当尽量减小均匀误差；如果发射率误差较大或者背景辐射较复杂，应当采用基于相位的检测方法。

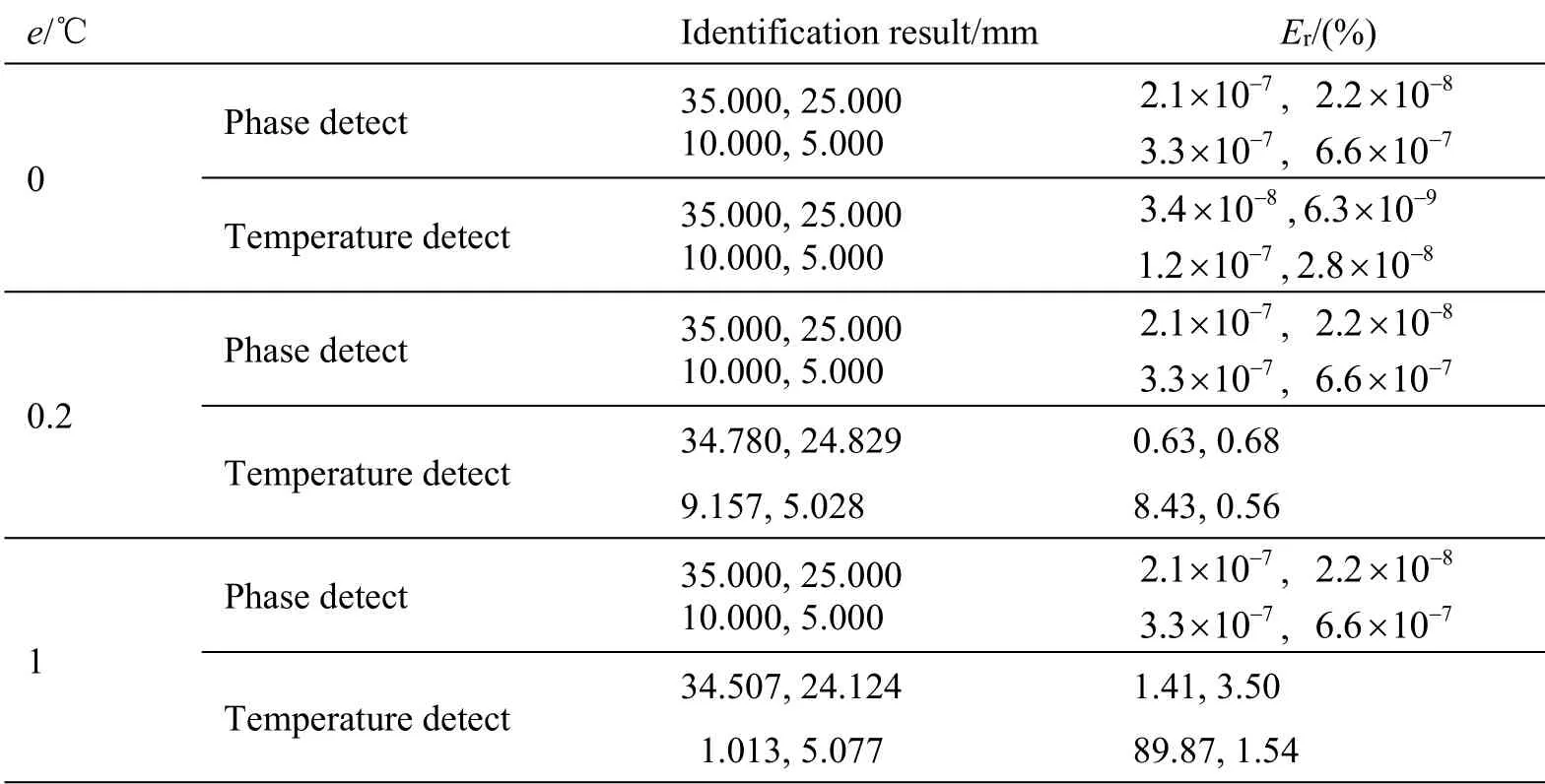
表4 不同均匀误差下的识别结果Table 4 Results in distinct uniform temperature errors

4 结论

本文将共轭梯度算法与脉冲相位和脉冲检测法相结合，实现了基于相位和表面温度的缺陷定量识别，对比分析了不同因素对识别结果的影响，得到的结论主要有：①当不存在测温误差时，在不同的初始假设下，基于相位与基于表面温度的识别方法都能准确地识别缺陷位置大小。

②在较小的随机测温误差下，基于相位与基于表面温度的识别都有很好的识别精度，但随测温误差的增大识别精度将降低。可见基于相位和表面温度的识别精度都对随机误差敏感。

③在不同的均匀误差下，基于相位的识别都能准确地识别缺陷位置大小；基于表面温度的识别结果在均匀误差较小时，有较好的识别精度，但随均匀误差的增大识别精度将降低。可见均匀误差对基于相位的识别无影响，而对基于表面温度的识别影响较大。因此，在实际检测时，如果采用基于表面温度的检测，应当尽量减小均匀误差；如果发射率误差较大或者背景辐射较复杂，应当采用基于相位的检测方法。