基于改进深度森林的电动执行器故障诊断方法

2022-06-22侯国莲吕志恒张文广吴凯利

自动化与仪表 2022年6期

侯国莲，吕志恒，张文广，吴凯利

（1.华北电力大学控制与计算机工程学院，北京 102206；2.上海新华控制技术集团科技有限公司，上海 270062）

电动执行器作为重要的调控部件，广泛应用在电力、航天、煤炭等工业领域中，其结构复杂且长期处于恶劣运行环境中，不可避免出现性能劣化以及故障，影响工业正常生产，甚至造成人员伤亡和财产损失[1-2]。因此，及时发现其故障并加以识别，对控制系统安全运行具有重要意义。

近年来，国内外学者对执行器故障诊断进行了大量研究。文献[3]针对单一诊断方法容易误判的情况，提出了一种基于证据融合的执行器故障诊断方法；文献[4]针对闭环控制回路反馈作用导致故障表现不明显的问题，提出了一种基于特征指标信息融合的诊断方法；文献[5]针对航天领域机电执行器提出了一种基于长短期记忆神经网络的故障诊断方法。

深度森林（deep forest，DF）是2017年提出的深度学习新算法[6]，目前已应用在生物信息、轴承故障诊断、电力系统稳态研究等领域[7-9]。文献[10]提出一种加权级联森林用于化工过程故障诊断；文献[11]通过主成分分析降低DF 特征维度，用于齿轮箱的故障诊断。

综上，本文将DF 算法引入电动执行器故障诊断领域，提出一种基于改进DF 的故障诊断方法。首先，对试验数据进行预处理；其次，基于改进的DF算法建立故障诊断模型，通过超参数试验确定了模型的最佳参数；最后，将所提方法与支持向量机（support vector machine，SVM）和一维卷积神经网络两种方法进行对比，验证了所提故障诊断方法的有效性。

1 深度森林模型

DF 是一种决策树集成学习算法[12]，主要包括多粒度扫描和级联森林（muti-grained cascade forest，GcForest）两部分。

1.1 多粒度扫描

多粒度扫描结构如图1 所示，核心思想是采用滑动窗口对样本采样。对于一组包含K 维特征的样本，通过一个长度为L 的滑动窗口进行滑动采样，每次滑动的步长为S，则滑动采样结束后会有N=（K-L）/S+1 个L 维的特征向量。将得到的所有子样本作为普通随机森林和完全随机森林的输入，则每种森林获得N 个维度为P 的概率向量。将这些概率向量拼接，构成了多粒度扫描的最终输出。

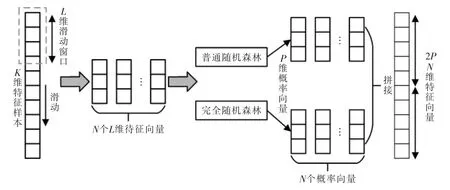
图1 多粒度扫描结构图Fig.1 Structure diagram of multi-granularity scan

1.2 级联森林

级联森林包含多个级层，每一级联层中包含若干个普通和完全随机森林，用于逐层处理数据特征。级联森林的整体结构如图2 所示。

在完全随机森林中，决策树随机选择一个特征在其分支节点上进行分割，直到每个节点仅包含相同的类；在普通随机森林中，决策树随机选择个特征进行分割（D 为输入特征的数量），并计算信息增益值，选择信息增益值最大的特征生长树。这样，每个决策树都输出一个类向量形式的结果，随后对随机森林中所有决策树的输出类向量取均值，即为随机森林的决策结果；最后，对同一级中所有森林决策结果取均值，取最大值对应的类别作为样本在该级联层的预测结果。

在图2 中，多粒度扫描的输出不仅作为级联森林的输入，而且会与级联森林每层输出拼接，构成增强特征作为下一级输入。这样层层迭代，每当扩展一个级联层，输入特征都经过k-折交叉验证，在验证集上进行诊断准确率评估，当分类准确率不再上升时，则停止训练。因此，级联森林能够根据数据集的大小自适应地确定模型层数，降低了人为调整参数的工作量。

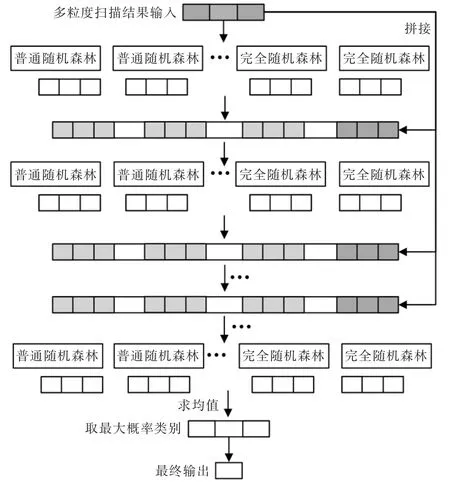
图2 级联森林结构图Fig.2 Structure diagram of cascade forest

1.3 改进的深度森林模型

当应用DF 算法解决故障诊断问题时，直接将预测结果拼接多粒度扫描结果作为下一级的输入，会造成特征向量冗余。为此，本文提出了一种基于D-S 证据理论的改进方法。

1.3.1 D-S 证据理论

D-S 证据理论使用概率对各个命题发生的可能性进行度量，能够处理不确定性问题[13-14]。 D-S 证据理论的识别框架中包含有限个基本命题，设同一识别框架下两个独立证据的基本概率分配函数分别为m1和m2，对应命题分别为｛A1，A2，…，As｝和｛B1，B2，…，Br｝，利用Dempster 组合规则得到证据融合后新命题的基本概率分配函数[15]，具体计算公式为

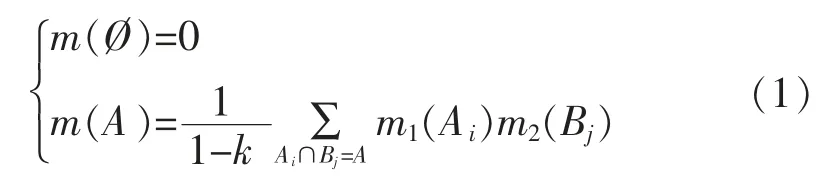
式中：A 为Ai和Bj融合后的新命题；m（A）表示命题A 的基本概率分配函数，为冲突系数，用来衡量不同证据对同一命题的相悖程度。

1.3.2 D-S 证据理论与级联森林结合

本文基于D-S 证据理论对级联森林改进，将每个森林视为独立证据体，根据Dempster 组合规则得到证据融合后这一级联层所有森林输出的融合特征向量。为了避免高冲突证据导致冲突系数为1 而无法计算概率问题，本文将随机森林决策结果进行转换得到各个命题的基本概率分配函数，具体计算公式如下：

式中：Ak表示情况类别；Mj（Ak）表示第j 个森林预测第k 类情况发生的基本概率分配函数；mj（Ak）表示第j 个森林预测第k 类情况发生的原始输出概率；n为当前级联层包含森林的总数。

通过上式获得各类情况在当前级联层的基本概率分配函数，然后根据公式（1）得到证据融合后的特征向量。为了弥补特征融合可能带来的信息缺失，随机选择一个森林决策结果与融合特征向量拼接，同时与多粒度扫描输出拼接作为下一级层的输入特征。改进后的级联森林结构如图3所示。

图3 改进后级联森林结构图Fig.3 Structure diagram of improved cascade forest

2 基于改进深度森林的电动执行器故障诊断

2.1 电动执行器信号特征提取

针对电动执行器监测数据含有噪声扰动，无法直接作为DF 算法输入的问题，本文基于时频域分析法提出一种特征提取方法。信号时域信息指标分为有量纲和无量纲两类，本文提取了数据集的7 种有量纲指标：方根幅值、均方幅值、均值、峭度、自相关系数、标准方差、变异系数；以及5 种无量纲指标：裕度、波形、脉冲、峰值和峭度。具体计算公式如表1 所示。此外，为了兼顾信号的频域信息，采用文献[16]提出的改进0 能量函数计算采样数据能量和能量熵。其中能量函数具体计算公式如下：

表1 信号时域指标含义Tab.1 Meaning of signal time domain index

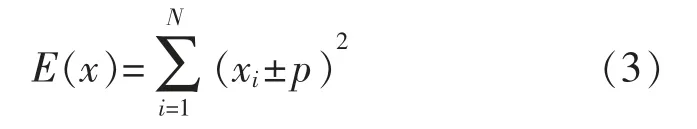
式中：N 为信号的长度；p 为一个较小的正值，本文取0.02；xi为正值时，加上p，反之减去p。

能量熵计算公式如下：

综上，本文提取了采样数据的12 种时域特征和2 种频域特征，为确保特征向量在相同范围内，对每个特征进行归一化处理，以构建原始特征向量。

2.2 深度森林诊断模型的构建

基于DF 的电动执行器故障诊断流程主要包括离线训练和在线故障诊断两个流程，如图4 所示。具体步骤如下：

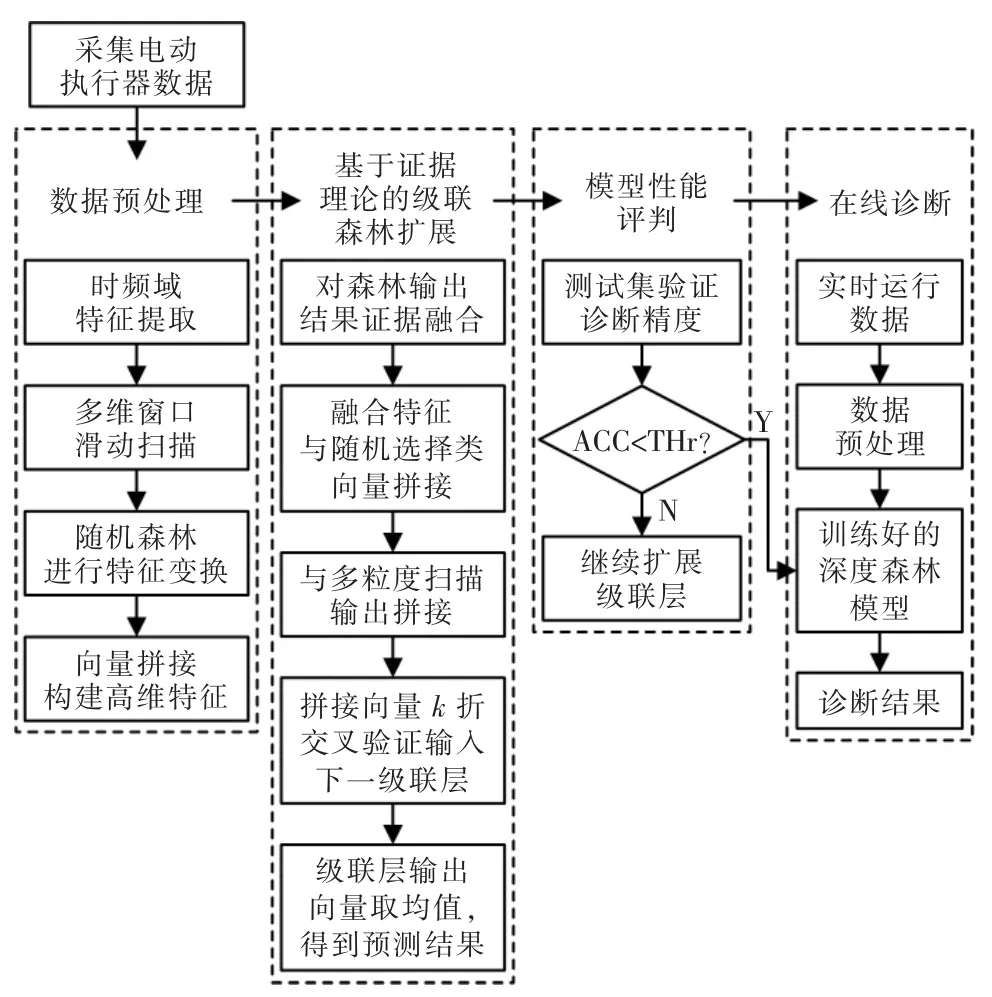
图4 基于改进深度森林的故障诊断方法Fig.4 Framework of fault diagnosis method based on improved deep forest

步骤1电动执行器流量信号预处理。首先对采集到的流量反馈信号进行时频域指标计算和归一化处理，再进行多粒度扫描得到高维特征向量；

步骤2离线训练级联森林。将步骤1 获得的高维特征输入到级联森林进行训练，每扩展一个级联层，都进行k-折交叉验证，并计算准确度，当准确度满足要求时停止训练；

步骤3在线故障诊断。将电动执行器实时监测的流量反馈信号经过步骤1 处理后输入到完成训练的级联森林模型中获得诊断结果。

3 试验分析

3.1 数据来源及故障试验

本文所采集的电动执行器流量信号来自实验室故障诊断试验平台，如图5 所示。本文基于试验平台模拟阀门阻塞、阀芯与阀杆脱开、阀座卡死和内部泄漏4 种典型故障，分别标记为F1，F2，F3，F4。通过改变故障注入时间、电动执行器初始阀位设定值、25 s 时阀位设定值进行不同工况下的电动执行器故障模拟试验，共采集4 种故障和正常状态在8 种工况下的执行器流量信号作为试验数据，共计400 组，每类状态包括80 个样本，每个样本长度为50000，工况设置情况如表2 所示。截取部分数据如图6 所示。

表2 不同工况描述Tab.2 Description of different working conditions

图5 基于dSPACE 的电动执行器试验平台Fig.5 Electric actuator experiment platform based on dSPACE

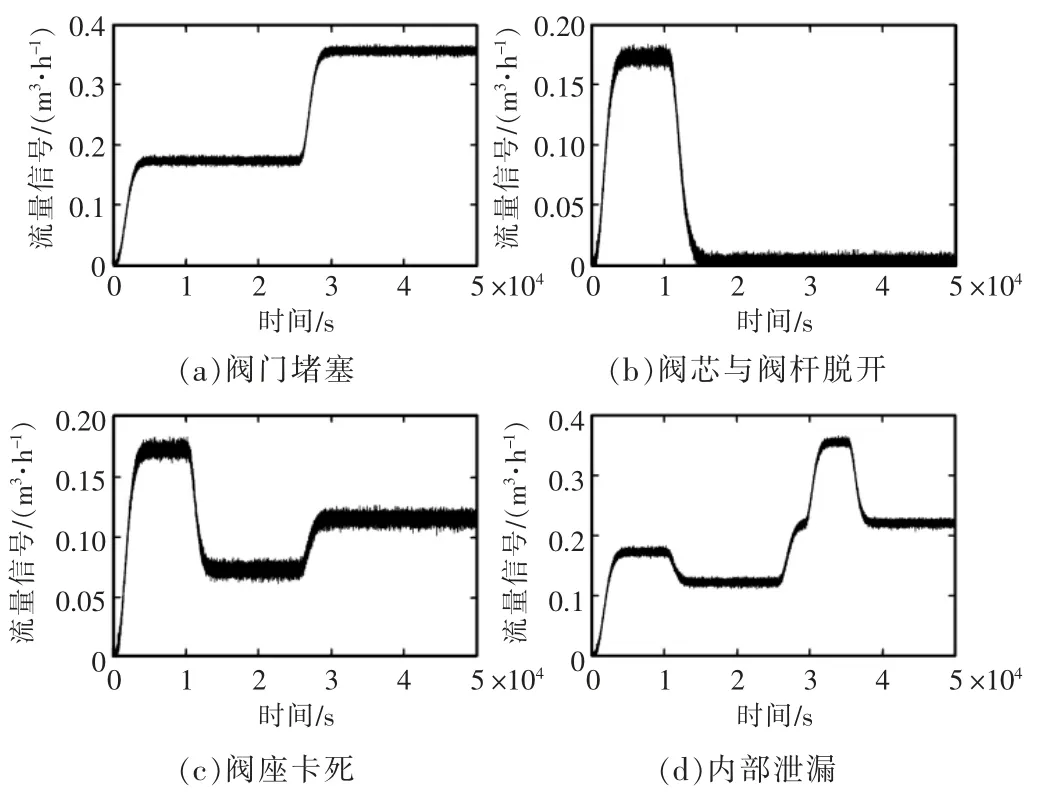
图6 故障模拟试验数据Fig.6 Faults simulation experiment data

3.2 超参数试验

多粒度扫描中超参数对诊断模型影响较小。根据经验设置，具体如下：1 个普通随机森林，1 个完全随机森林，每个森林中决策树数量为60，滑动窗口大小为4 和8。级联森林中，为了平衡不同森林的分类结果，设两种森林及其包含决策树个数一致，k-折交叉验证设为4 折。由于电动执行器数据集较小，增加决策树数量会造成诊断模型结构的冗余，因此将随机森林中决策树个数设为60。每种随机森林的个数决定了DF 模型的整体复杂度，相较于决策树对模型更具影响，因此本文针对随机森林数量展开研究。森林个数从2 开始增加，为了避免偶然因素的干扰，每增加一次算法都运行20 次，取每次k-折交叉验证结果的均值作为准确率，记录每次算法运行时间，并在试验结束时记录其均值，试验结果如表3 所示。

表3 表明，增加随机森林个数能够有效提高诊断准确率，但同时也会增加模型复杂度，导致训练时间随之递增，并且当森林个数达到5 个以后，诊断准确度稳定在94.0%左右。因此，综合模型诊断准确率和训练时间因素，考虑降低运行内存消耗，将每种随机森林个数设为5 个。

表3 随机森林数量试验结果Tab.3 Results of random forest number experiments

3.3 结果分析

为了验证本文提出的基于改进DF 的电动执行器故障诊断方法，使用3.1 节获得的电动执行器多种工况下执行器流量信号进行诊断，根据3.2 节确定的模型参数构建级联森林。故障诊断方法根据某次k-折交叉验证结果整理出的混淆矩阵，如图7 所示，可以看出本文方法在测试样本集上的分类准确度为96.2%，整体诊断准确率较高。

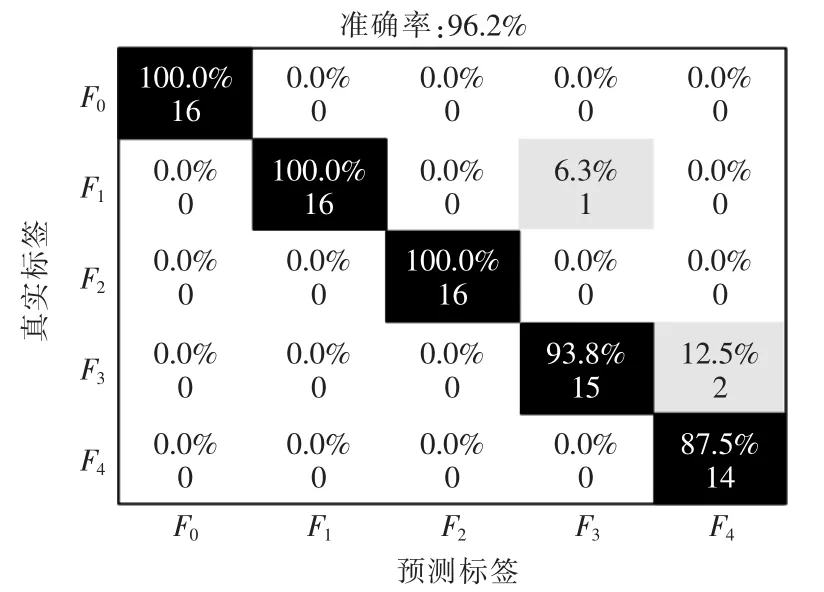
图7 故障诊断混淆矩阵Fig.7 Confusion matrix for fault diagnosis

为验证所提方法的有效性，设计多个对比试验方案：

方案1基于粒子群算法优化SVM 的故障诊断方法。粒子群算法用于SVM 的罚参数和核参数寻优，其范围分别为［0.1，50］和［0.1，50］，其它参数设置如下：迭代次数为200、粒子群大小为50、最大权重为0.9、最小权重为0.3、学习因子c1=c2=2。输入到SVM 中的数据是前文所述的时频域特征。

方案2无改进的GcForest 算法。其参数设置与3.2 节一致。

方案3基于一维卷积神经网络的故障诊断方法。模型整体结构按Lenet-5 网络设置，卷积核大小设置为24，激活函数为ReLu，优化算法为Adam，学习率为0.001，迭代次数为100 次。

使用上述3 种对比方案进行试验。本文将准确率、精度、召回率和F1值4 个指标用于评价上述3个方案诊断准确性、误判和漏判情况，结果如表4所示。

表4 不同诊断方法与本文方法性能对比Tab.4 Comparison of diagnosis performance between the other diagnosis methods and proposed method

从表4 可以看出，SVM 算法用时最短，但诊断能力最差，这与数据特征提取相关，说明通过多粒度扫描提取多级特征的必要性；一维卷积神经网络诊断效果较好但用时最长，这说明深度神经网络在参数优化上耗时太长，而DF 所需数据集更小，参数鲁棒性更好；未改进的GcForest 算法在评价指标和运行时间上的表现都不如本文模型，说明了D-S 证据理论克服级联森林特征冗余缺陷的可行性。