基于时间最优的机器人多路径点轨迹规划

张华文，刘子亮

（1.河南省工业机器人应用工程技术研究中心，南阳 473000；2.河南工业职业技术学院 自动化工程学院，南阳 473000；3.天地上海采掘装备科技有限公司，上海 201401）

为了避免机器人运动过程中发生碰撞，往往需要在起始点和终止点之间插入一些中间点来约束机器人的运动。 合理的轨迹规划可使机器人运行平滑，减少机械冲击，同时让机器人在通过这些中间点时不用停止，达到最优的运行时间，提高工作效率[1]。 文献[2]构造了关节空间下经过中间点的五次多项式轨迹规划函数，并利用MATLAB 仿真计算出机器人运动过程中各关节参数-时间曲线， 但运行过程中加速度变化并不平滑。 文献[3]对五次多项式函数插值方法中轨迹中间点角速度的设置方法提出改进， 能使关节角速度和角加速度更加平滑，但是没有考虑运行时间最优的问题。 文献[4]以工业机器人搬运作业为研究对象，完成了关节空间中的轨迹规划实施过程，并就多项式插值的效果进行了对比，但在中间点各关节速度都降为零，降低了运行效率。 文献[5]和文献[6]基于遗传算法和高次多项式来实现时间最优的轨迹规划，提高了轨迹跟踪精度，但是算法较为复杂，增加系统的运算负担。

本文采用基于加速度连续过渡的线性规划方法，将路径点用直线连接起来，每两个路径点之间的运动看作是匀速运动，每个运动段之间用加速度连续变化的运动进行过渡。 该算法只需向前看一个路径点就可以将整条运动轨迹计算出来， 计算量小，便于编程实现。

1 两点运动的轨迹规划

用qi和qf分别表示起始和终止时刻关节角度向量和分别表示第j 个关节起始和终止时刻的关节角，kv和ka分别表示关节最大速度向量和关节最大加速度向量，kvj和kaj分别表示第j 个关节的最大速度和最大加速度。 每个关节的最大速度和加速度通常可以根据该关节的电机参数得到。

在qi和qf之间的轨迹规划可以用式（1）表示：

式中：D=qf-qi。 规划算法的目标是求出r（t）的表达式。

1.1 关节同步系数的计算

首先对梯形速度运动进行分析，位移表达式如式（2）所示，其中τj表示加速段时间。

对速度进行时间的积分，得到梯形的面积，即为运动的距离，如式（3）所示：

求得关节j 最小运行时间为

所有关节需要在相同的时间内完成各自的运动，为了达到同步的效果，每个关节需要根据运动距离、关节能够达到的最大速度和加速度来调整运行时的最大速度和加速度[7]。 设定任意一个关节为参考关节，然后为每个关节设定最大速度同步系数λj和最大加速度同步系数υj。 关节j 的最大同步速度为λjKvj，最大同步加速度为υjKaj。 下文先以两个关节为例说明同步系数的求解。

两个关节的最小运行时间为

同步后的运行时间为

根据式（6）可得：

最大同步速度不可能超过最大运行速度，因此最大速度同步系数需满足：

根据式（7）可得：

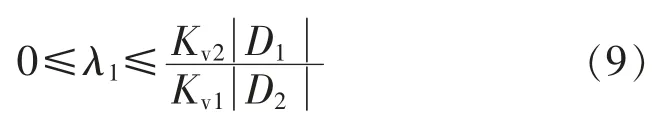
与之对应的加速时间为

推广到n 个关节可得：

根据式（7）可以得到其他所有关节的同步系数。

1.2 二次抛物线加速度的轨迹规划

与梯形速度运动相似，二次抛物线加速度运动也分为加速、匀速和减速3 个阶段。 但是其加速度不是恒定的， 而是关于时间的二次抛物线函数，如图1 所示。 这样，保证了加速度、速度和位移的连续，有效地减少冲击，确保机器人的平滑运动。

图1 二次抛物线加速度运动模型Fig.1 Quadratic parabola acceleration motion model

根据条件可知，在加速运动段，关节j 的位移、速度和加速度应满足以下5 个条件：

由这5 个限制条件，可以推出位移、速度和加速度关于时间的表达式：

式中：1≤j≤n，0≤t<τ′。 加速度在t=τ′/2 处取得最大值：

由式（15）可知，二次抛物线加速度运动的加速时间是梯形速度运动加速时间的1.5 倍。 在匀速时间段h′中，位移关于时间的表达式如下：

式中：τ′≤t<τ′+h′。

比如，某学生屡屡迟到，传统做法可能是，了解学生迟到原因，帮助学生找到避免迟到的方法，同时辅以必要的惩戒。而设计思维的做法是引导学生对人生有目标，对学习感兴趣，对班级产生归属感，对交往有渴望等，然后再根据这些更高层次的目标设计解决方案。

减速段和加速段是对称的，即：tf′=2τ′+h′。

根据式（13）和式（15）可得加速段运动的距离为

得到整段的运行时间为

为了能达到最大的同步速度，运行距离必须满足：

如果该条件不能满足，必须降低最大运行速度，新的最大运行速度为

2 多路径点的轨迹规划

为了避免机器人运动过程中发生碰撞，往往需要在起始点和终止点之间插入一些中间点来约束机器人的运动。 使用q1，q2，...，qm表示一段轨迹中的所有路径点。 根据第1 节中的方法，假设过每个路径点的速度都为0，可以计算得到同步系数和加速段时间τk′，其中k 代表由qk和qk+1所组成的段。

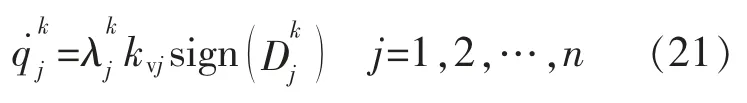
假设第k 段之间是匀速运动，则第k 段的运行时间hk为

为了生成一条在中间路径点不停止的平滑轨迹，需要在k-1 段和k 段之间进行平滑过渡，如图2所示。 在第k 个路径点的过渡段的时间为2Tk。 为了保证加速度的连续，需要用一个二次函数来表示过渡段加速度的变化。 在过渡段，每个关节都以能够达到的最大加速度运行，以保证轨迹能够尽可能地逼近中间点。 过渡时间的表达式如下：

图2 关节空间加速度连续过渡的线性规划Fig.2 Interpolations with continuous acceleration blends in joint space

式中：k=2，3，…，m-1；j=1，2，…，n。

所有关节只在整个轨迹的起始点和终止点的过渡是同步的，根据式（15）可计算得到起始点和终止点的过渡时间Tkj=τ′/2。

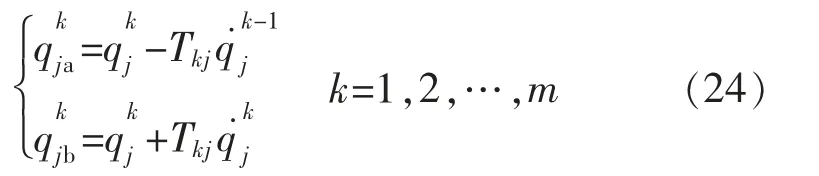
为了方便表示，用Tk代表Tkj。如图2 所示，关节j 在第k 段中匀速段的位移关于时间的表达如下：

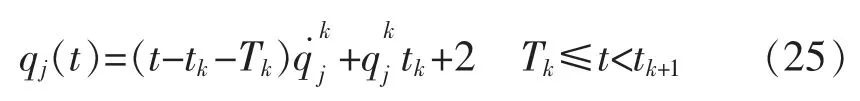
考虑第k 个点的过渡段，有以下几个限制条件：

根据上述条件，可以得到关节j 在第k 段中过渡段的位移关于时间的表达式是一个四次多项式，表达式如下：

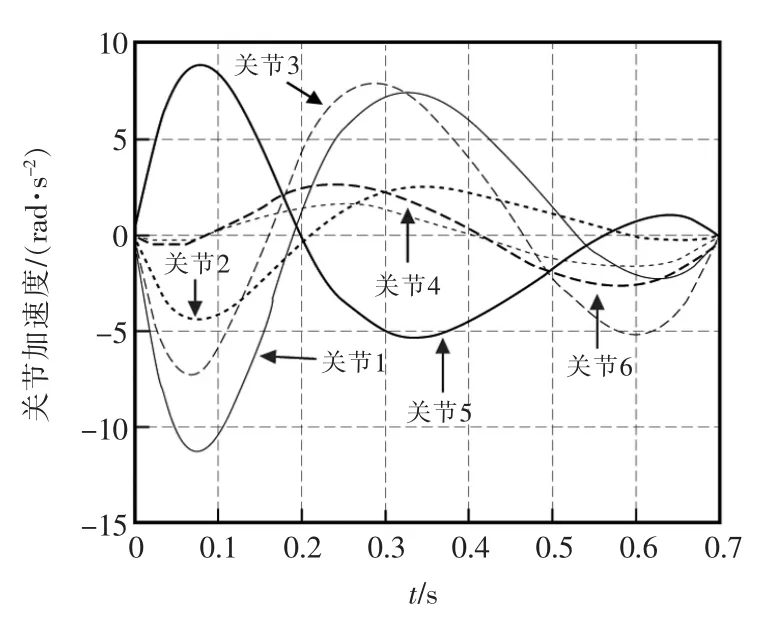
式中：tk≤t

速度和加速度关于时间的表达式如下：

加速度在t=tk+Tk处取得最大值：

根据最大加速度kaj，该表达式可用来计算Tk。需要注意的是，必须满足hk≥Tk+Tk+1。如果该条件不满足，需要降低该段的运行速度，重新进行规划。

3 算法设计

过路径点的关节空间的轨迹规划算法流程如图3 所示。

图3 多路径点的关节空间的轨迹规划算法流程Fig.3 Flow chart of trajectory planning with via points in joint space

算法在实现时有以下几个关键点：

（1）必须保证每个关节运动的同步。

（2）需要判断每段的距离是否满足hk≥Tk+Tk+1，如果不满足，则重新计算该段的运行速度，重新进行规划。 可能会出现不论怎样调整速度，都无法完成规划的情况，此时程序便陷入死循环。 因此，需要设定循环次数上限，如果循环达到上限后，仍然无法完成规划，则程序给出相应提示。

（3）在计算插补点时，为了确定时刻t 的位移，首先要确定t 所处的时间段。为了提高查找效率，可以使用二分法判断t 所在的时间段。

4 实验结果与分析

使用MATLAB 进行算法仿真验证。分别在时刻0 s，0.2 s，0.7 s 处设置3 个示教点，如表1 所示。

表1 示教点参数Tab.1 Teaching point parameters

设定插补周期为0.01 s，可得到各关节角度、速度和加速度的变化曲线。 由图4 可知，各关节位移变化平滑连续且运动同步，终止点位置精确。由图5可知，各关节以逼近最大速度运行，变化连续且运行同步，初始速度和终止速度均为0。 由图6 可知，各关节加速度呈现二次抛物线变化方式，变化连续且运行同步， 最大运行加速度逼近关节最大加速度，初始加速度和终止加速度都为0。 结果表明，该算法能够根据教点正确规划各关节的运动轨迹；确保各关节能够同步运行；位移、速度和加速度都能够平滑连续的变化，提高运行平稳性；速度和加速度都能够逼近关节最大值， 有效地优化运行时间，提高运行效率。

图4 关节角度变化曲线Fig.4 Joint angle curve

图5 关节速度变化曲线Fig.5 Joint velocity curve

图6 关节加速度变化曲线Fig.6 Joint acceleration curve

5 结语

以六自由度工业机器人为研究对象，分析只有起始和终止两点的运动轨迹，为实现各关节运动同步引入速度和加速度同步系数2 个参数，为保证运行平衡采用二次抛物线加速度运行方式推算出位移、速度和加速度关于时间的表达式，并给出运行限制条件；分析多路径点的运动轨迹，把每两个路径点之间看作是匀速运动，每个运动段之间用加速度连续变化的运动进行过渡；分析算法设计的关键点，给出算法流程；使用MATLAB 进行算法仿真验证。

该算法保证了多路径点运动中各关节的加速度、速度和位移的变化平滑连续，实现各关节同步运行和时间最优，确保机器人能够平滑高效地运行。 通过将轨迹分解成多个低阶多项式的方法有效地降低运算复杂度，减小运算量，易于编程实现。