液压驱动机器人速度控制的研究

刘广亮，肖永飞，赵永国，孙 洁

（齐鲁工业大学（山东省科学院） 山东省科学院自动化研究所 山东省机器人与制造自动化技术重点实验室，济南 250014）

移动机器人驱动方式有多种形式，主要包括电机驱动，液压驱动和气压驱动等。 其中液压驱动方式具有动力大、力与惯量比大、快速响应性高、易于实现直接驱动等特点，适用于承载能力大、高功率密度比、抗冲击以及防爆工作环境。 与电机驱动和气压驱动相比， 液压驱动具有更高的功率密度，能够满足机器人野外运输所需的高负重及快速运动需求，同时液压驱动系统可以采用内燃机提供能源动力，通过添加燃料进行快速补给，具有长时间的续航能力， 比电能源机器人更适合从事野外作业。目前广泛应用于四足、六足、多足等腿足式机器人以及煤矿井下机器人[1-4]。

由于液压系统具有时滞性、强非线性、时变负载性的特点，所以液压机器人的速度控制精度一直是难点问题，在此方面研究人员开展了很多研究工作。文献[5]提出基于RBF 神经网络的自适应最优控制系统。 文献[6]提出采用非线性特性分段校正方法来提高机器人控制性能的方法。 文献[7]研究了液压负载补偿与跟踪误差补偿结合的力控制方法，将阀控系统与泵控系统结合成新型的泵阀复合驱动系统，既降低系统的能量损耗，又保证了液压驱动单元响应速度和响应精度。

本文主要针对移动机器人的液压驱动启动死区、各个比例阀不均衡等非线性与时变负载问题，对液压驱动的机器人速度精确控制进行研究。 采用分段补偿和分段线性校正方法，设计了两轮速度同步补偿算法，实现移动机器人两轮液压马达的同步控制，经验证机器人精度控制性能得到很大改善，速度控制精度和控制响应提升明显。

1 机器人独立两轮差速运动学模型

独立两轮差速运动学模型如图1 所示，全局坐标系｛XOY｝，局部坐标系｛X′O′Y′｝。 局部坐标系Y′轴与两轮的中轴线重合，方向从右轮指向左轮。 X′轴方向为机器人的正前方。 假设机器人质心C 位于两驱动轮轴线的中点，与坐标系原点O′重合。 局部坐标系相对于全局坐标系的旋转角为θ， 为机器人的方向角。

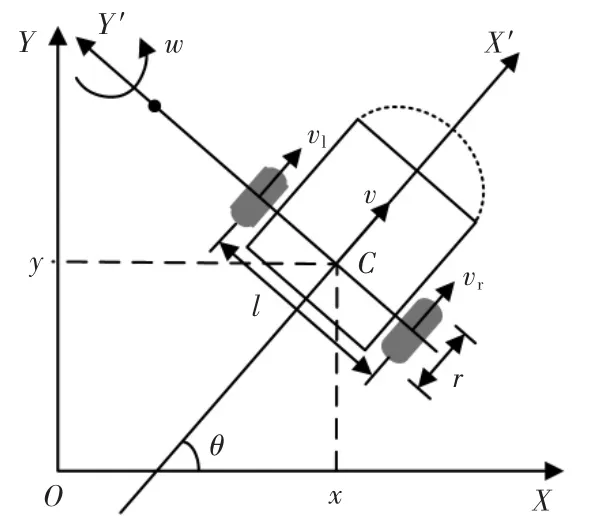
图1 两轮差速运动学模型Fig.1 Kinematic model of two-wheel differential drive

局部坐标系到全局坐标系的映射正交旋转矩阵为

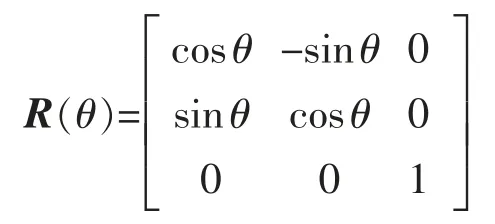
假定两驱动轮轴线的长度为l， 左右驱动轮半径都为r，机器人的位姿向量为p=（x，y，θ）T。 两轮差速驱动移动机器人的正运动学方程[8]为

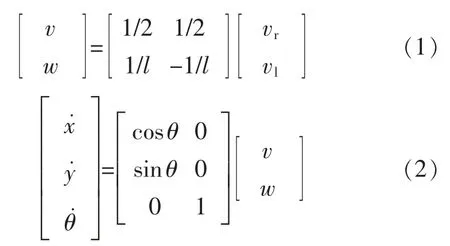
式中：v 为机器人质心C 处的线速度；w 为机器人的转向角速度；vr，vl分别为机器人的左右驱动轮线速度。

在全局坐标系下，机器人的代表点C 的位置和姿态可以通过式（2）中的速度关系式积分求得：

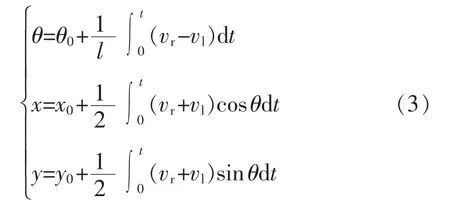
在航迹演算中根据式（3）计算机器人姿态轨迹。

假设相邻时间段内机器人曲线航迹近似为直线，如图2 所示[9]。 同时假设机器人不是全向移动，只是前进和旋转，不能纵向移动。 机器人两个相邻运动时刻在采样周期内运动距离短，可以将轨迹看作匀速直线运动，也就是说机器人在Δt 时间内沿局部坐标系X′轴移动了vΔt， 在全局坐标系统中移动距离为

图2 相邻点轨迹的直线近似Fig.2 Linear approximation of adjacent trajectory points

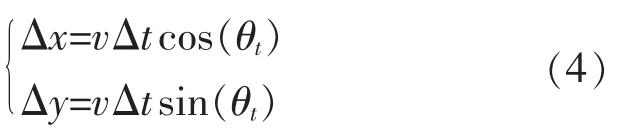
那么，t+1 时刻机器人姿态为

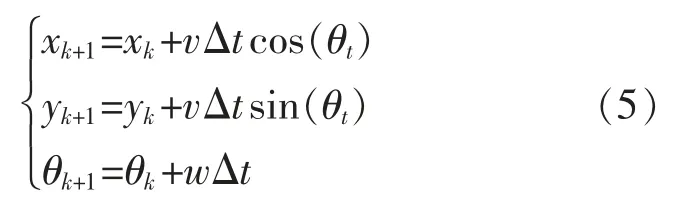
根据式（1）可知机器人中心点线速度v 为

角速度w 为

若vr=vl，机器人轨迹为直线段；若vr≠vl，机器人轨迹为圆弧。

机器人的逆运动学可以根据正运动学式（1）、式（2）及式（6）、式（7）求得。

即：

通常给定机器人中心点的线速度和角速度，然后根据式（8）、式（9）推出左右两个驱动轮的线速度，也是机器人的驱动电机线速度vr，vl与机器人线速度v 及和角速度w 间的关系。

在控制系统驱动电机时，需要将驱动电机线速度转换为电机的转速值。设电机的转速为n，单位为r/min，线速度的单位为m/s，由于：

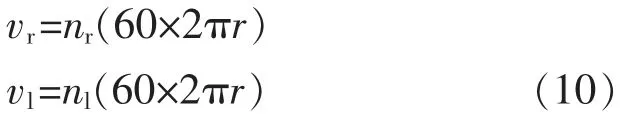
则有：

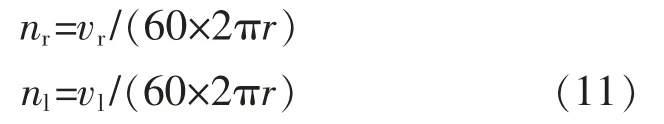
式中：nr，nl分别为差速运动时左右轮转速值，单位为r/min。

2 最大速度与加减速限制

为了实现液压机器人平稳精准的运动，需要对机器人速度和加速度进行规划[10]，确保机器人在运动过程中速度不突变，平稳过渡，从而避免出现机器人机械冲击和失步震荡。 同时由于机器人本体机械性能限定了机器人的速度范围，超出速度限制的指令将是无效的，因此需要通过速度最大值限制方式对机器人速度、加速度、加加速度进行加减速控制[11]。

2.1 最大速度

差速运动控制系统中（如ROS 的差速运动控制器[12]）需要配置速度的最大最小值vmax，vmin，最终速度值为

式中的vmax，vmin在实际应用中分别包括左右轮各两个速度：机器人线速度和角速度。 从式（8）可知线速度和角速度要转化为两轮的转速n。 而对每个特定的驱动电机转速是有限制的（假设为最大转速为nmax），即线速度和角速度合并后的两轮转速n 不能大于两轮的最大转速nmax，所以在设定机器人本体的最大线速度和角速度的时候需要考虑与驱动电机最大转速之间的匹配。给定一个机器人线速度v，那么在驱动轮最大转速的限制下就会有一个wmax，如果角速度指令超出这个wmax值，机器人也只能按wmax执行转向，结果会造成机器人转向不足。

假设驱动轮的最大转速为nmax，那么根据式（11）得到两轮最大线速度：

再根据式（6）、式（7）可知机器人的线速度和角速度最大为

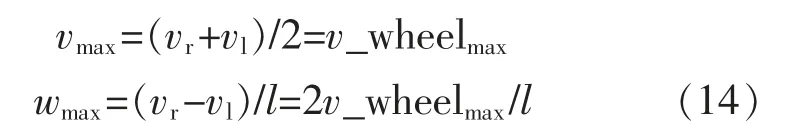
但是这两个最大值不可能同时达到，当转向速度最大达到wmax时：

根据式（6），此时机器人线速度v=0。 而当线速度最大达到vmax时：

再根据式（7），此时机器人角速度w=0。

假设给定机器人额定线速度v~， 如果其中一个驱动轮（如右轮）达到最大转速，则此时另一个驱动轮（左轮）速度为

此时机器人角速度w 为

因此在机器人驱动电机最大转速限制下，机器人角速度与线速度存在制约关系，如图3 所示，需要根据实际需要分别设置机器人移动的线速度和角速度，并保证线速度和角速度合并后不会超过驱动电机最大转速限制。

图3 角速度与线速度之间的制约关系Fig.3 Constraint relation between angular and linear velocity

2.2 加速度控制

在机器人加减速控制中可以根据S 曲线加减速法[13]进行配置。 假设差速运动控制器中配置加速度的最大最小值分比为amax，amin，vk，vk+1，时间差为Δt，那么Δt 时间内对应最大最小速度变化值分别为dvmax，dvmin，那么：

最后速度：

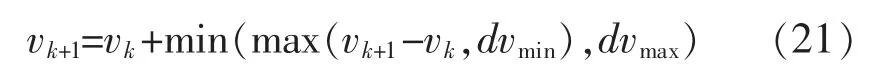
2.3 加速度控制

同理，假设差速运动控制器中配置加速度的最大最小值分别为jmax，jmin，vk，vk+1时间差为Δt，那么Δt 时间内对应最大最小加速度变化值分别为damax，damin，那么：

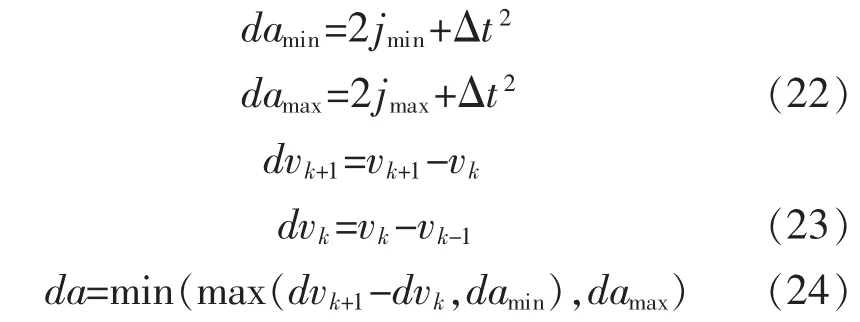
最后速度：

3 液压驱动机器人速度控制

3.1 液压驱动速度控制存在的问题

由于液压系统的时滞性和时变负载性，造成液压驱动与伺服电机驱动有很大不同，首先液压马达具有启动阈值（死区），输入值低于启动阈值马达不运转，其次移动机器人的两个液压马达，存在流量分配不均匀的问题，即给两个液压马达同样的输入指令值，左右液压马达运行速度快慢不一样，并且在前进方向和后退方向也存在输出比例不一致的问题。

如图4 所示，对机器人左右轮前进与后退方向进行速度的测试，从得到测试数据分析可以看到左右轮输入启动阈值不同，前进方向左轮启动阈值约385，右轮启动阈值约357（注：液压控制器输入最大值1000）。输入输出比也不一致，同样的输入左轮慢右轮快。 并且左右轮在前进方向和后退方向，启动阈值也不同，右轮在前进方向启动阈值为357，后退方向启动阈值都是385。 图4 充分显示了液压系统的输入输出的非线性特点。

图4 左右轮原始速度数据分析Fig.4 Analysis of two wheel original velocity data

3.2 速度控制模型

在机器人自主控制时，必须保证驱动电机的线性输出，即同样输入指令机器人的左右轮以及前进和后退都应该是同样的输出，这样才能保证液压机器人平稳准确运行，为此构建基于分段线性拟合的液压机器人输入输出模型如下：

式中：c 为启动阈值；vin为输入值；k 为系数；下标r，l表示右轮和左轮； 下标b，f 表示前进和后退。 如kfr表示前进方向右轮系数。

将整个液压系统划分为左右轮和前进后退方向4 种情况分别进行分段数据线性拟合和分段线性校正，从而获得拟合参数，见表1。

表1 速度控制模型拟合参数表Tab.1 Parameters of velocity control model fit

然后在首次拟合的基础上，进行多组机器人样机试验验证分析，在同时兼顾左右轮和前后方向匹配，获取最终的优化参数，见表2。

表2 速度控制模型优化参数表Tab.2 Optimized parameters of velocity control model

4 实验验证

4.1 液压机器人样机

液压机器人样机如图5所示，为履带式内燃机驱动机器人。

图5 液压驱动机器人Fig.5 Hydraulically driven robot

液压驱动部分采用EPEC 液压控制器控制比例阀，完成对液压马达的转速控制。 内燃机的发动机为洋马2TNV70-PYU，发动机功率7.3 kW，转速2400 r·min-1，液压系统采用力士乐，液压流量20 L/min，液压系统压力25 MPa。 机器人驱动轮距0.8 m，驱动轮直径0.285 m。

4.2 实验结果分析

对采用优化参数的液压机器人样机对进行了测试，结果如图6 所示，实验结果表明在相同输入下左右轮、前进方向、后退方向速度输出基本匹配一致，具有线性关系。

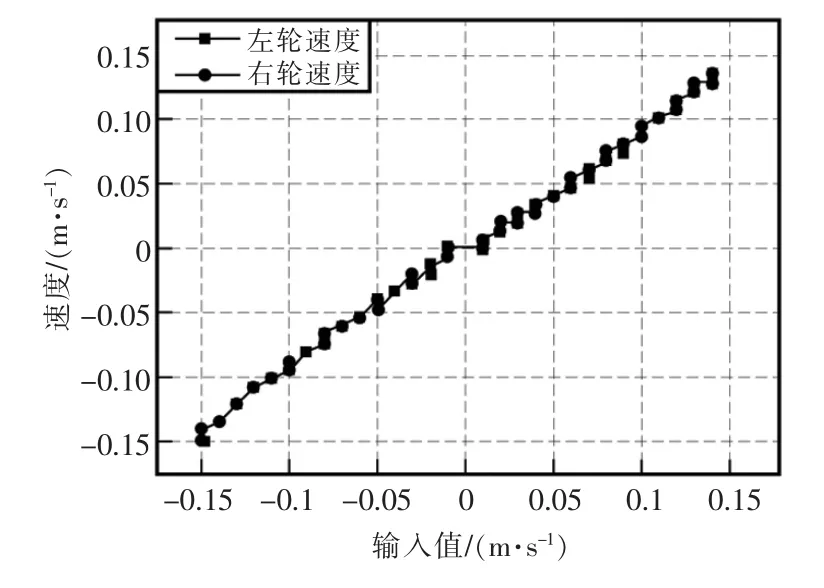
图6 左右轮速度对比Fig.6 Comparison of left and right wheel velocity

5 结语

液压驱动机器人具有动力性能好，越野能力强的特点，特别适用于特种作业环境，但是液压驱动控制模型复杂，精确控制难度大。 本文在分析了机器人差速运动控制理论模型和加减速控制基础上，详细研究了液压驱动速度控制模型，采用分段数据线性拟合和校正的方法，对机器人速度控制参数进行了优化，并应用于内燃机驱动液压机器人，经测试验证机器人运行平稳可靠。