螺旋槽动压径向气体轴承承载特性研究*

2022-06-22王洪涛董志强

润滑与密封 2022年6期

王洪涛董志强

(太原科技大学机械工程学院山西太原 030024)

螺旋槽动压气体轴承因摩擦因数小、清洁和可以适应任何环境等优点，以及较大的承载性等，被广泛使用于电子机械、食品机械、医疗机械、高温气体循环机及燃气透平机，计算机磁能等领域[1-3]。

研究人员对螺旋槽气体轴承的润滑性能进行了深入研究。李树森等[4]采用数值模拟的方法研究了动静压气体轴承参数变化时对静态特性以及气膜压力变化的影响。戚社苗等[5]采用偏导数法得到了刚度和阻尼系数，通过数值模拟的方法研究了扰动频率对这些系数的影响。于普良等[6]研究了一种新型径向槽结构，并且对气体轴承进行了数值模拟，得到了槽的深度以及半径对气体轴承承载力的影响。虽然目前对螺旋槽气体轴承润滑的研究很多，但是对螺旋槽动压径向气体轴承的研究并不多[7-12]。

本文作者从Navier-Stokes方程以及连续性方程出发，得到了气膜压力分布的基本方程以及承载力特性，基于CFD技术，采用流体动力学和Fluent软件，直接求解气体润滑基本方程Navier-Stokes方程，弥补了雷诺方程在气体流动形态方面的不足；运用SolidWorks软件建立了三维螺旋槽动压气体轴承物理模型，通过mesh对气膜区域进行网格划分，得到了压力分布并分别研究了转速、槽长、槽深比、槽数、半径间隙以及偏心率和承载力之间的关系。

1 螺旋槽径向动压气体轴承模型建立

图1所示为螺旋槽动压径向气体轴承工作面展开图及结构简图。图中L为螺旋槽长度，D为直径，β为螺旋角，是螺旋槽与中心轴承截面的夹角，e为偏心距，bg和br分别为槽宽和台宽，h为平均气膜厚度。各个槽关于中心截面对称，由于轴承要承受径向载荷，所以主轴工作的时候，主轴与轴承产生偏心距离e，轴承和轴颈并不能重合。偏心率ε=e/h。Ob为轴承的坐标中心，Or为轴颈的坐标中心。轴承几何参数如表1所示。

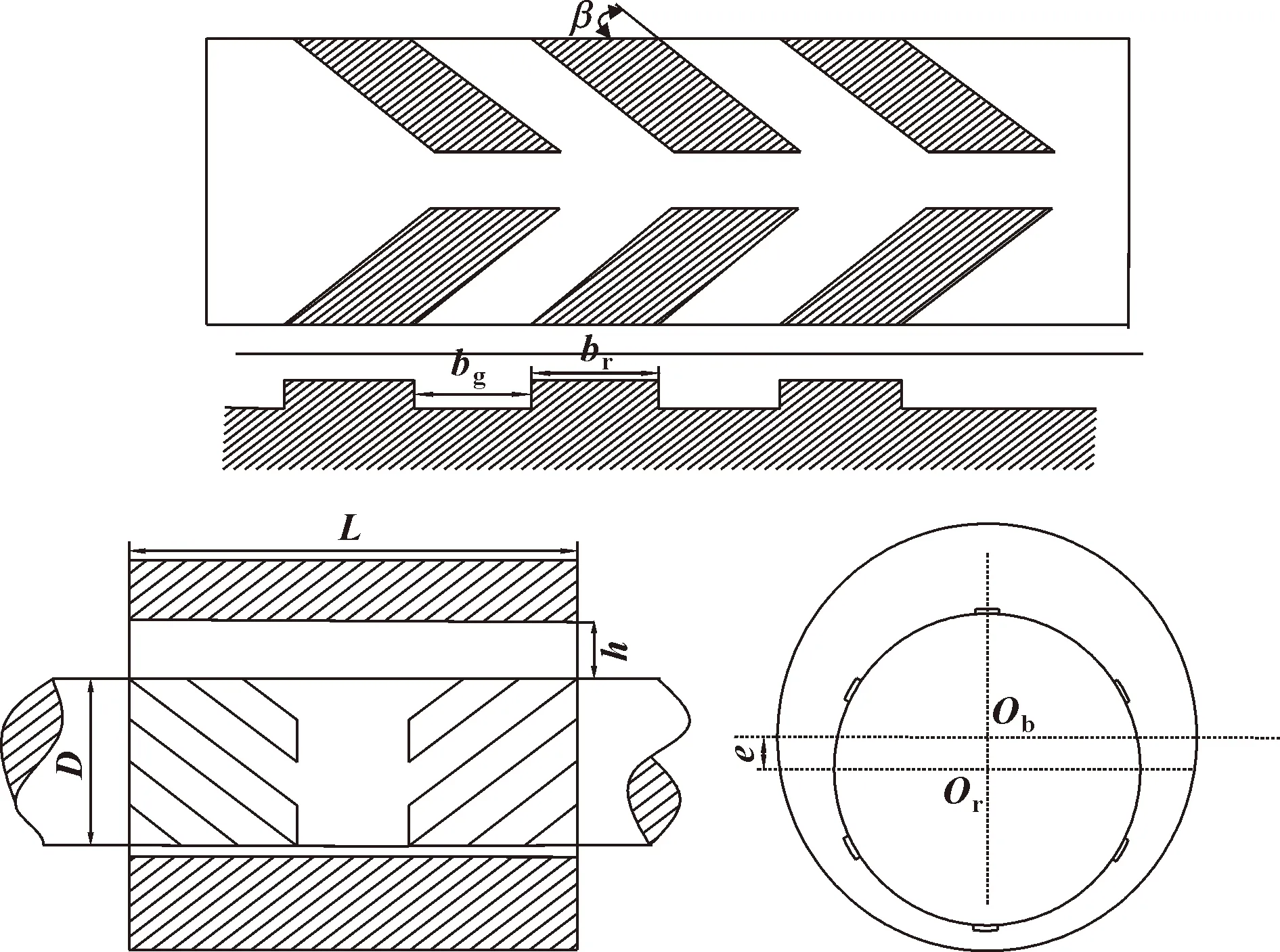
图1 螺旋槽动压径向气体轴承工作面展开图以及结构简图Fig.1 Working face and structure diagram of spiralgroove dynamic pressure radial air bearing

表1 螺旋槽动压径向气体轴承几何参数Table 1 Geometric parameters of spiral groove dynamic pressure radial air bearing

2 雷诺方程的推导

流体动力润滑的研究，实际上就是对Navier-Stokes方程的研究。在黏性流体中取出一微元体，如图2所示，三条边分别为dx、dy、dz，气体在坐标点x、y、z处的密度为ρ,压力为p，速度在坐标轴上的3个分量分别为u、v、w。根据牛顿第二定律和气体分子运动理论，推导出式(1)所示的Navier-Stokes 方程[13]。

图2 微元体上的表面力

(1)

式中:X、Y、Z分别表示单位的体积力沿x、y、z轴方向的分量。

(2)

其中:

(3)

式(3)表示速度的散度。

当气体动力黏度η为常数时，式(1)可简化为以下方程:

(4)

研究轴承气膜压力的承载特性，就需要求出决定气膜压力的方程式，这可由状态方程式、连续性方程求出。

状态方程式为

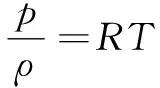
(5)

气体连续性方程为

(6)

在螺旋槽动压径向气体轴承中，气膜厚度和轴承尺寸相差太大，所以为便于更好地推导出雷诺方程，还需对气体动压润滑做出以下假设[14-17]:

(1)由于气膜厚度相对于其他尺寸非常小，因此轴承表面的曲率可以忽略掉，误差仅为0.1%左右。

(2)沿润滑膜厚度方向上的压力变化可忽略不计。

(3)假设气膜流动为层流，不存在涡流和湍流。

(4)忽略惯性力和离心力等作用。

(5)气膜上无外力作用。

(6)气体在固体截面上无滑动。

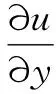
将以上假设代入式(4)，得:

(7)

(8)

对式(6)、(7)、(8)进行积分，经整理，化简得：

(9)

式(9)为可压缩气体的非定常雷诺方程式。

由于轴承润滑气膜表面沿着气膜的法向基本不运动，所以式(9)可简化为

(10)

在一般情况下，只研究螺旋槽气膜表面间的相对运动，故式(10)可简化为

(11)

式(11)是研究轴承气膜压力分布的基本方程。

(12)

(13)

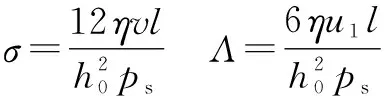
所以式(13)可写为以下形式：

(14)

式中:σ为挤压数；Λ为压缩数或轴承数。

螺旋槽径向动压气体轴承承载力为

(15)

(16)

(17)

螺旋槽结构系数

(18)

螺旋槽动压径向气体轴承总承载力为

(19)

3 螺旋槽动压径向气体轴承Fluent分析

3.1 螺旋槽径向气体轴承分析流程

螺旋槽动压径向气体轴承Fluent仿真计算流程如图3所示。图4所示为螺旋槽空气动压轴承三维模型，由于气膜的平均厚度属于微米级别，所以选用精度较高的三维建模软件SolidWorks进行物理建模。而流体区域是通过在ANSYS Workbench的DM模块中运用Fill命令对流道区域进行抽取，如图5所示。

对于螺旋槽径向气体轴承模型气膜区域网格的划分，由于轴承气膜厚度为微米级别，轴向尺寸在毫米级别，尺寸量级差别非常大，况且模型还存在偏心结构，因此不能采用周期性对称的方法分析。为保证在气膜厚度上有合适的网格和一定的求解精度，文中利用Edit Geometry in Spaceclaim软件将气膜区域分为48个区，利用mesh对整个气膜采用结构化划网格的方法，先在面上划面网格，再到体上划体网格，最后对槽区和台区进行分层。经过多次尝试，发现划分5～6层达到的效果较好[18]。气膜网格划分如图6所示。

图3 螺旋槽动压径向气体轴承Fluent仿真计算流程Fig.3 Fluent simulation flow of spiral groovedynamic pressure radial air bearing

图4 螺旋槽空气动压轴承物理模型Fig.4 Physical model of spiral grooveair dynamic pressure bearing

图5 流道区域Fig.5 The flow channel area

图6 流体区域网格划分Fig.6 Fluid region meshing

3.2 边界条件的设置

把计算域的外壁面设置为静壁面，内壁面设置为旋转壁面，与轴承轴线做偏心分布，其速度值为主轴的旋转速度，左右两边分别设置为压力进出口，介质为空气，进出口压力分别为0.101 MPa(一个大气压)，如图7所示。

图7 边界条件示意Fig.7 Schematic of boundary conditions

3.3 网格无关性验证

为获得较高的精度并减少计算量，进行网格无关性验证，如图8所示。随着网格的增多，承载力先增长后趋于平稳，考虑到工作效率和精度要求，选用655 680网格数目进行计算。

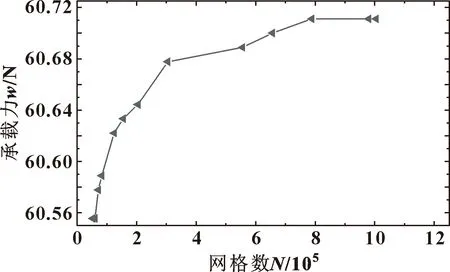
图8 网格无关性验证Fig.8 Grid independence verification

4 Fluent仿真结果及分析

4.1 模型验证

为验证数值计算的准确性，文中对采用有限差分法与有限元法得到的压力分布进行对比。图9(a)所示为采用有限差分法对雷诺方程进行求解而得到的压力云图[19]，图9(b)所示为数值计算方法得到的压力云图。

图9 不同方法计算的压力云图对比Fig.9 Comparison of pressure cloud images with different methods:(a)finite difference method[19];(b)numerical method

通过对比图9中压力云图可以发现，有限差分法与有限元法得到的压力分布规律是一致的，在偏心的地方都出现了最大值和最小值。由此可以说明，理论分析与数值模拟分析得到的压力变化趋势是一致的，证明了数值模拟的准确性。

4.2 转速对气膜压力的影响

为分析转速对螺旋槽动压气体轴承的影响，在ε=0.3，转速分别为10 000、15 000、20 000、25 000、30 000 r/min工况下，对螺旋槽动压气体轴承气膜压力场进行了仿真，结果如图10所示。

由图10可以得出，在偏心方向气膜厚度最小，压力相对其他区域较大，说明轴承旋转所产生的动压效应非常明显。由于空气的流动，气膜厚度由大变小时就会形成楔形流道，动压效应增强。在气膜厚度较大处，压力相对较小，这是由于动压效应相对较弱，使得压力减小，从而使气膜在偏心方向上形成压力差，产生承载力。比较5种速度下的压力云图可知，随着转速的提高，最大压力值逐渐增大，这是因为转速的提高，使螺旋槽空气动压轴承的动压效应更加显著。

图10 不同转速下的气膜压力流场云图(ε=0.3)Fig.10 Cloud diagram of gas film pressure flow field at different rotating speeds(ε=0.3):(a)n=10 000 r/min；(b)n=15 000 r/min；(c)n=20 000 r/min；(d)n=25 000 r/min;(e)n=30 000 r/min

4.3 槽长和槽数对承载力的影响

图11所示为不同偏心率下槽长对承载力的影响。

图11 不同偏心率下承载力随转速的变化Fig.11 Variation of bearing capacity with the lengthof slots at different eccentricity rates

承载力随着槽长的增长而增大，且偏心率越大，则承载力增大越明显。这是由于在相同转速下，偏心率越大，则在偏心率方向气膜厚度就越小，使得空气流速减小，因而增加了螺旋槽内的动压效应，压力变大，因此使得气膜的压力差增大，增大了承载力。在偏心率相同的情况下，槽长增大，承载力增长，这是由于槽长的增加，使得产生流体动压效应的区域增加了，因而使得气膜压强在偏心方向上的压力差增大了，承载力增大。

图12所示为不同偏心率下槽数对承载力的影响。

图12 不同偏心率下承载力随槽数的变化Fig.12 Variation of carrying capacity with the numberof slots at different eccentricity rates

在相同偏心率下，承载力随着槽数的增加而增大，这是由于槽数的增加使得气膜沿着气体轴承周向的变化速率增加，导致动压效应变强。槽数相同时，随着偏心率的增大，承载力同样变大，这是因为气膜厚度的减小，使得压力差逐渐变大，承载力变强。

4.4 转速对承载力的影响

图13所示为不同偏心率下轴承转速对承载力的影响。在偏心率一定的情况下，随着转速的增加，承载力呈现明显加快的增大趋势，这是因为随着转速的增加，气膜截面的变化率增大，螺旋槽空气动压轴承的动压效应迅速增强，气膜压力差值增大，承载能力也因此大幅度提高。在低转速时，承载力随着偏心率的增大变化幅度不大，转速较高时，承载力随着偏心率的增大而大幅度增大。

图13 不同偏心率下承载力随转速的影响Fig.13 Influence of bearing capacity with rotatingspeed at different eccentricity rates

4.5 偏心率和半径间隙对承载力的影响

图14所示为不同偏心率下槽深比对承载力的影响。在槽深比一定的情况下，承载力随着偏心率的增加而逐渐增大。这同样是由于偏心率的增加，使得气膜动压效应增强，承载力变大。在偏心率一定的情况下，随着槽深比的增加，承载力也在增加，这是由于当槽深比不断增大时，气体经过螺旋槽时产生的阻力会增大，使得动压效应增强，因此承载力增大。