研发约束、不确定性与全要素生产率*

杨 灵，于 洋，蔡冬冬，冯荣凯

（1.沈阳工业大学 经济学院，沈阳 110870；2.辽宁大学 经济学院，沈阳 110136）

近十年来，随着创新驱动战略的实施，我国不断加强研发（R＆D）投入强度，2019年已经达到2.23%，接近发达国家水平。与R＆D投入增长形成对比的是全要素生产率（TFP）和技术创新并没有出现显著的进步，以TFP表征的技术进步和经济发展甚至呈现出波动下降的迹象［1］。本文在中国整体和省级层次上，对R＆D投入水平、TFP及区域经济发展之间的关系进行理论上的论证和实践上的测算和检验，试图找到目前R＆D投入增长和TFP提升不匹配的原因，寻求经济增长新动力。

与以往的研究相比，本文的创新之处在于：（1）在TFP测算方面，以往学者基于行业异质性采用了异质性随机边界模型，而本文将异质性运用在省级面板数据上；（2）以往国内外学者主要在公司层面上运用异质性随机边界模型研究R＆D融资约束，而本文将R＆D整体水平作为TFP的约束；（3）首次使用随机边界模型来界定和测算R＆D产出的不确定性。

一、文献综述

关于R＆D与经济发展关系的文献，最早可以追溯到1776年Adam提出的科技对发展社会生产力至关重要的观点［2］。运用模型研究R＆D与经济发展的关系始于Cobb和Douglas，他们将技术进步加入生产函数中［3］。1956年，Solow和Swan在假设技术进步为外生给定的条件下，建立了Solow-Swan模型，提出只有技术进步才能保持经济增长，但该模型无法解释长期经济增长的形成［4］。为克服这一缺点，Romer和Lucas提出内生增长理论，建立了内生增长模型，此后的研究模型多是在此基础上发展起来的［5－6］。

TFP的实质就是用于衡量经济产出与发展的生产效率，在单投入和单产出的情况下就是“投入产出比”，只不过现实经济中必然是要素投入组合，于是就有了TFP和TFP增长率的测算。在测度全要素生产率的方法方面主要有索罗余值法、数据包络分析法（DEA）、扩展索罗余值法、随机边界生产函数法（SFA）等。索罗余值法模型简单，但其假设技术进步外生和规模报酬不变，且对投入要素度量不足，目前较少应用。DEA和SFA运用的都是边界面方法，起源于Farrell的开创性工作［7－8］。根据距离函数表达式的不同，DEA是利用数学规划进行的非参数方法；而SFA则是通过随机生产边界函数对生产行为的刻画求得技术效率的参数方法。

自从内生增长模型发展起来以后，研发约束就成为一个重要的研究主题。Schultz［9］、Solow［4］和Griliches［10］最先用实证研究证明了R＆D对经济生产和经济增长的重要性。此后，众多学者从宏观和微观两个层面在这个主题上进行了大量研究：宏观上主要是通过R＆D投入影响TFP的计量核算来表证R＆D和经济增长的关系；微观上则是在公司层面考察R＆D和生产效率的关系。特别是20世纪80年代以后，随着内生增长理论的复兴，大量关于R＆D与生产效率或经济增长关系的文献涌现出来。Griffith等运用OECD国家的面板数据发现，R＆D在OECD国家TFP增长率收敛的过程中起到了关键性的作用［11］。Coccia关于R＆D与生产率的研究发现，65%的生产率方差应该归咎于研发投入占GDP的比例，从而证明是R＆D投入和创新（过去是资本积累）形成了公司和国家的竞争优势［12］。Bravo-Ortega等运用包括32个发展中国家在内的65个国家1965—2005年的数据，证明了人均R＆D投入增加10%将导致长期TFP提高1.6%［13］。Bektas等和Necati等的研究都得出了相近的结论［14－15］。

国内关于R＆D与TFP的研究文献一直较多。唐保庆从R＆D投入与溢出等方面扩展了CH模型，以APEC中17个成员为研究对象，运用动态面板数据模型研究了R＆D与TFP之间的关系，得到了具有稳健性的正向关系的结论［16］。曹泽和李东证明了不同类型的R＆D投入对TFP的增长均具有正向促进作用，只是R＆D活动的溢出效应不同［17］。柳建平和程时雄证明了本国各行业的R＆D资本投入对TFP均有显著的正向影响［18］。孙晓华等发现并检验了R＆D影响TFP的行业异质性问题［19］。王晓娆和李红阳对中美各类R＆D活动执行部门对TFP效果的影响进行了比较性研究［20］。焦翠红和陈钰芬运用空间计量考察了区域TFP增长和R＆D活动之间的关联特征，发现中国区域TFP增长和R＆D活动均存在明显的正向空间相关性和空间俱乐部特征［21］。邱爱莲等运用Malmquist指数分析法测算制造业全要素生产率指数，并指出加工贸易可以显著提高制造业全要素生产率［22］。王青等运用DEA模型，从时间角度评估出生产性服务业技术进步增长率均呈现先下降后上升的趋势［23］。姜国庆等采用非参数的DEA方法，测算出东北三省2002—2014年科技投入存在6.3%的资源浪费，并指出科技投入产出效率总体增长不快的原因是资源配置未得到有效优化［24］。

二、模型建立、变量选择及数据处理

1.异质性随机边界模型的建立

随机边界模型的基本形式为yit＝f（xit，t）·exp（vit－μit），通过最大似然法进行估计，其对数表达式为

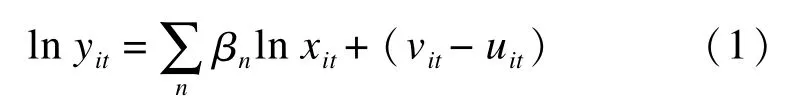
式中：yit为产出项的实际国内生产总值；xit为投入项的资本和劳动投入；β为待估参数；vit为服从的随机误差项，用来反馈主观能力以外无法控制的因素，包括测量误差和统计噪声带来的影响；uit为可控制但却没有达到生产边界面的部分，在本文中表示研发约束效应。由于其具有单边分布效应的特征，故假设其服从非负的截断型半正态分布，即。vit和uit与自变量无关，相互之间独立。为了表征异质性特征，设定），其中

式中：b0和b1均为常数项；δ和γ为外生解释变量的系数待估值。式（1）、（2）构成了异质性的随机边界模型，这一设定为后续分析提供了很大的灵活性：其一，可以同时分析外生变量对R＆D约束效应本身（μit）及其不确定性的影响，现有文献中分析TFP的随机边界模型都是这一模型的特例；其二，借助这一模型，可以定量分析R＆D约束导致的TFP损失，这是前期研究中基于其他设定无法实现的。各省份的TFP可用i的实际产出期望与随机产出期望的比值来确定，计算公式为式中，TEit表示第t年第i个省份的TFP，TEit越接近于1，说明效率越高。在对模型进行最大似然估计时，可以利用参数γ＝σu2／（σu2＋σv2）的显著性来确定模型设定的合理性：γ趋近于1，说明外生因素占主导地位；相反，γ趋近于0则说明随机误差的影响占主导地位；γ等于0时意味着不存在无效率项，可以直接用最小二乘法OLS进行参数估计。一般而言，γ值至少要大于0.5，较高的γ值也说明模型选择的可靠性。在本文实证分析所设置的各个模型中，γ值都接近于1，故没有再对其进行说明。

2.变量选择与数据说明

以2000—2015年我国除西藏外的30个省、自治区及直辖市的产出、投入以及相关影响要素为研究样本①由于西藏数据缺失较多，故样本数据为包含30个截面的面板数据。，产出指标为各地区人均真实GDP，投入分为资本投入和劳动投入，外生影响指标包括研发资金投入、技术市场成交额和三项专利授权量。具体指标如下：

（1）产出变量为地区生产总值。为消除价格因素的影响，本文以1997年为基期，采用地区生产总值指数对各地区历年的产出进行平减，得到地区实际生产总值，用来衡量真实的经济产出。

（2）资本投入：采用固定资本形成总额来度量，为保证数据的可比性，使用永续盘存法，参照单豪杰的研究结果，以1978年为基期的固定资产价格指数为平减指数，采用10.96%的资本折旧率计算得到。

（3）劳动投入：某一年的劳动投入为该地区的平均受教育年限与总就业人数的乘积。

（4）外生约束变量：研发投入和技术成交额经过GDP指数进行了平减处理。

（5）外商直接投资：利用外商直接投资额来衡量。

外商直接投资与专利授权存在正向关系，但并未达到共线性。以上数据中，除研发资金投入取自科技统计年鉴外，其余数据均来自中国统计年鉴，在代入模型前均进行了对数处理，描述性统计结果如表1所示。

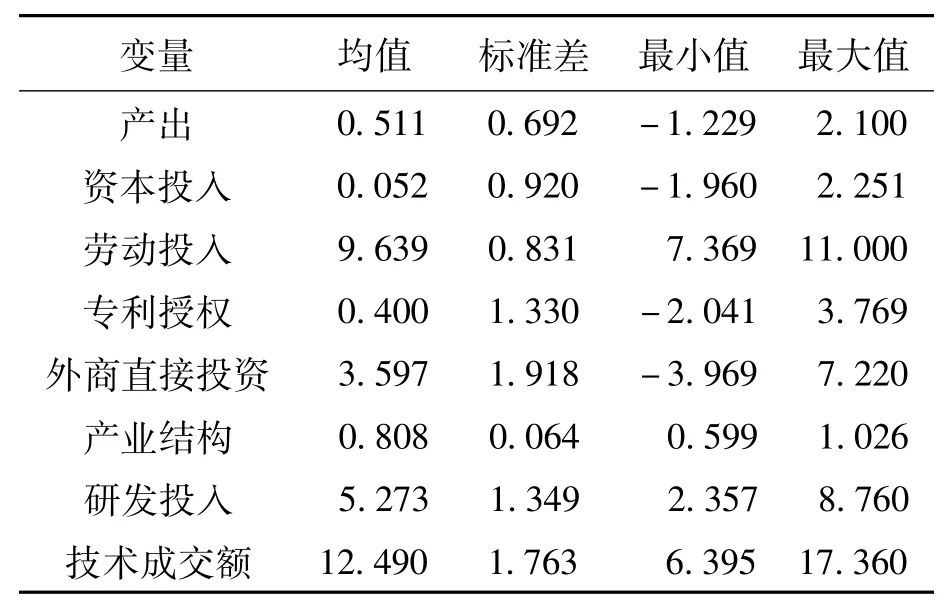
表1 变量的基本统计量

三、实证分析

1.异质性随机边界模型估计

多种设定下的估计及检验结果如表2所示。

表2 异质性随机边界模型估计及检验结果

表2（续）

模型1是本文讨论的重点，其没有对异质性随机边界模型的参数施加任何约束。模型2～5是在模型1的基础上施加各种约束条件后得到的。模型2假设研发投入、三项专利授权数、技术成交额、外商直接投资和产业结构对R＆D约束的不确定性没有影响，对应着Battese和Coelli的设定方式［25］。模型3是假设变量对R＆D约束本身没有影响。模型4对应着Caudill等的模型，假设研发约束服从在零处截断的异质性半正态分布［26］。模型5是作为对比，假设不存在异质性下的投入产出随机边界模型。

整体而言，在所有设定方式下，资本投入都在1%水平上显著，而劳动投入除在模型3和模型4下不显著外，均在1%水平上显著。这表明，TFP一方面取决于资本与劳动的投入，同时也受到R＆D状况的影响。由表2可知，无论将检验的原假设设定为“不存在R＆D约束”（LR1）还是设定为“存在异质性R＆D约束”（LR2），最终检验结果都表明异质性随机边界模型1显著优于其他4个模型，尤其显著优于模型5，表明研发约束及其不确定性对TFP具有显著影响。故本文后续分析均基于模型1展开。

由表2可知，三项专利授权数在R＆D约束方程和R＆D不确定性方程中均在1%水平上显著为负，表明专利授权数量的增加不但可以缓解R＆D对TFP的约束，还可以明显降低R＆D影响产出结果的不确定性。这一结果与唐德祥等、胡求光等和张豪等的研究结论一致，即研发投入对TFP起到主要作用［27－29］。同时，这也与前期多数文献对R＆D与经济发展关系的分析结论一致，如王维国等、罗凤鹏等均发现R＆D投入对经济发展的作用显著［30－31］。

研发投入在R＆D约束方程中在1%的水平上显著为负，在不确定方程中在1%水平上显著为正，表明研发投入的增加可以显著缓解R＆D对TFP及经济发展的约束，但同时却显著增加了R＆D的不确定性。

技术市场成交额在R＆D约束方程中不显著，但在不确定性方程中在1%的水平上显著为负，说明技术市场成交额没有形成研发约束，对TFP没有直接影响，但能显著降低研发的不确定性，所以对于TFP以及经济发展还是有着明显的间接作用。

产业结构在R＆D约束方程中在1%的水平上显著为负，在不确定性方程中在5%的水平上显著为正，说明产业结构升级可以显著缓解R＆D对TFP及经济发展的约束，但同时也增加了R＆D结果的不确定性。前半部分的结论与多数文献基于产业结构升级和经济发展的研究结果是一致的，后半部分的结论尚未见到相关方面的文献。

外商直接投资在R＆D约束方程中在1%水平上显著为负，在不确定方程中不显著，表明外商直接投资可以显著缓解R＆D对TFP及经济发展的约束，即外商直接投资对于R＆D有着显著的溢出作用，这与目前多数关于外商直接投资和R＆D关系的文献结论是一致的［32］。

2.地区差异分析

地区R＆D水平能够从一定程度上反映研发对经济发展的约束程度。为此，将30个省、自治区及直辖市按地区分成三组，并分别估计了异质性随机边界模型（5）、（6）。由于样本数量的关系，在分地区的估计中，为了能够让最大似然估计收敛去掉了两个变量，即产业结构和外商直接投资，估计结果如表3所示。

表3 分地区估计结果

对比三个地区的估计结果可以发现，三项专利授权数量在不同地区发挥的作用存在较大差异。就研发约束而言，三项专利授权数量能够显著缓解中部和东部的研发约束，而对西部的影响则不显著。这主要源于西部地区的整体研发能力相对较低，致使其对TFP和经济发展的约束有限。在研发不确定性方面，三项专利授权数量能显著影响西部的不确定性，但对中部和东部的影响却不显著，说明西部地区还处在研发初级阶段，其研发成果的作用尚未体现出来，通俗地讲，就是尚未发展到能够形成约束的阶段。

研发投入在R＆D约束方程中在1%的水平上显著为负，说明研发资金投入的增加可以显著缓解R＆D对TFP及经济发展的约束。在不确定性方程中，西部在1%的水平上显著为正，而在中部和东部并不显著，说明研发资金投入在显著降低对西部约束的同时，显著加大了研发作用结果的不确定性。

R＆D约束方程中，技术成交额在西部和中部都在1%的水平上显著为负，东部则在1%的水平上显著为正，表明技术成交额的增加能显著降低R＆D对西部和中部的约束，但却显著增加了对东部的约束。而在不确定性方程中，西部和中部的作用都不显著，只有东部在10%的水平上显著为负，表明技术市场成交额的增加能够降低东部的不确定性。

整体而言，对于处在不同发展阶段的地区，在R＆D约束作用方面，R＆D水平的提高是能够显著降低R＆D对TFP和经济发展的约束作用的，但对于经济发展相对落后地区的作用并不明显；而在R＆D不确定性方面，R＆D水平的提高对于降低研发结果不确定性的效果并不显著，但对经济发展相对落后地区其作用比较复杂，增加研发投入可以加大不确定性，增加R＆D专利则能显著降低不确定性。

3.TFP效率分析

面板随机边界分析可以定量分析每一个地区的TFP，间接反映地区发展所面临的R＆D约束程度。图1绘制了TFP的频数分布情况，由于最高TFP的样本较多，致使图形没有表现出完美的正态分布特征。TFP的样本均值和标准差分别为0.846和0.082，从整个分布来看，多数地区的TFP值都集中在0.75～0.90，表明R＆D约束使各地区TFP最优水平降低了10%～25%。

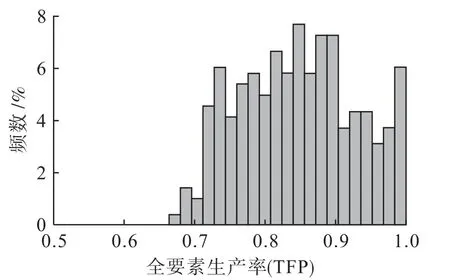
图1 全要素生产率指数的频数分布

不同地区的发展差距备受关注，本文按照人均三项专利授权数量将样本分为大规模、中等规模和小规模地区，进而分年度估算这三类地区的平均全要素生产率指数TFPI（见图2）。从图2a来看，2000—2015年样本总体TFP呈现持续上升的态势，基本介于75%～93%之间，这似乎表明中国整体R＆D水平呈现出一个较快的发展过程。

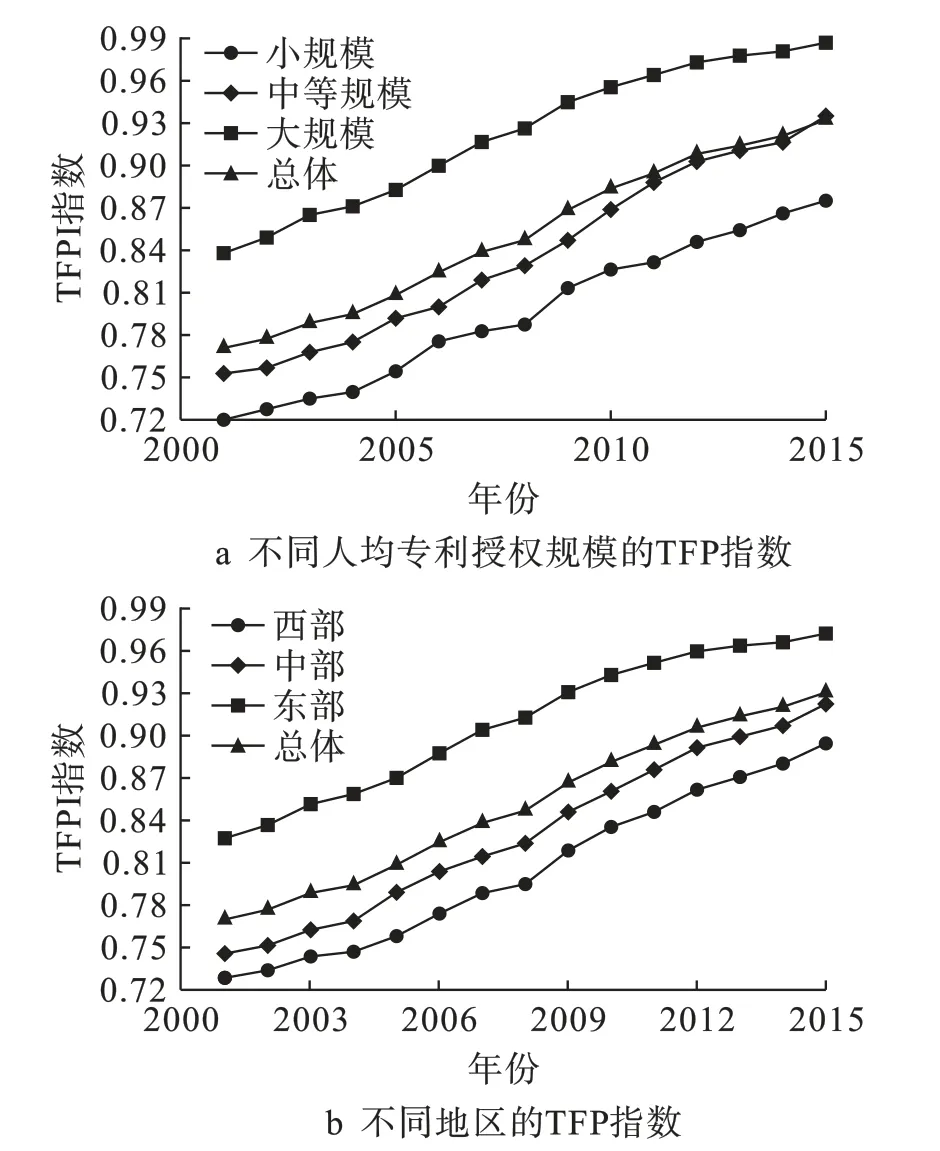
图2 全要素生产率指数对比

对比不同人均专利授权数量地区的TFP，尽管各种规模上都呈现出持续上升态势，但人均专利授权数量最多地区的TFP最高，小规模地区的TFP最低，中等规模地区的TFP介于两者之间。因为人均专利授权数是一个衡量研发水平的比较客观的指标，可以明确地说，R＆D对于TFP或经济发展起着核心推动作用，R＆D不同水平对应着经济的不同发展阶段，低水平的R＆D对经济发展有着显著的制约效应。图2b中不同地区与图2a中不同人均专利授权规模的TFP指数表现出较强的一致性，证明了本文得出的结论。

四、结论与建议

R＆D水平对全要素生产率（TFP）和经济发展有着重要的影响。在技术市场完美假设下，区域投入产出处于最优水平上，而R＆D约束的存在使得TFP和区域经济会单边偏离这一最优水平。本文利用这一特点，可以克服前期R＆D与TFP实证研究存在的诸多缺陷，同时可以定量分析R＆D约束对TFP及经济发展的影响。

本文实证结果表明：（1）R＆D约束的存在使得中国整体TFP比最优水平降低了10%～25%，平均TFP为0.846。（2）在区域经济发展中，三项专利授权数量的提升、产业结构的升级、研发投入和外商直接投资的增加，不但能缓解R＆D水平对TFP和经济发展的约束，还可以降低后续研发结果的不确定性；技术成交额的增加虽然不能降低R＆D对TFP和经济发展的约束，但是可以降低R＆D产出的不确定性。（3）R＆D水平较高地区和东部地区面临的R＆D约束和R＆D不确定性较低，而R＆D水平较低地区和西部地区面临较高的R＆D约束和R＆D产出的不确定性。

据此，提出如下政策建议：（1）R＆D发展水平确实对TFP和经济发展形成了制约，而且R＆D产出存在着较大的不确定性，即中国现阶段的经济发展已经开始对R＆D形成了决定性依赖。所以在区域经济层面应当努力提升R＆D整体水平，并且有效降低R＆D产出的不确定性。（2）有效的研发投入与三项专利授权数量具有同步的一致性效应，所以在加大研发资本投入的过程中，应参照三项专利授权数量的提升来判断资本投入的有效性；重视外商直接投资没有问题，但更应该重视外商直接投资的结构，因为外商直接投资结构与产业结构一样都会影响R＆D的发展水平；应淡化技术成交额的指标性作用。（3）由于东部地区已经进入高水平的良性循环发展阶段，西部地区依然面临着严重的R＆D约束和不确定性，所以如果能够在更高水平上制定R＆D政策，使西部和中部能够借力东部R＆D成果，将对中西部地区乃至中国经济的整体发展产生更为深远的意义。