基于新SEIRS 的矿工不安全行为传播分析

李红霞，方开元

（1.西安科技大学 应急管理学院，陕西 西安 710600；2.西安科技大学 管理学院，陕西 西安 710600）

煤矿安全一直是我国安全生产的重要部分。近年来我国煤矿百万吨死亡率大幅下降，但煤矿死亡人数仍占我国高危行业死亡人数的半数以上。据多名学者研究统计，矿工的不安全行为是导致煤矿安全事故频发的主要原因[1-2]。因此研究矿工的不安全行为及传播对煤矿安全具有重要意义。

刘轶松[3]从人体心理状态的角度将不安全行为分为有意和无意2 类，并指出有意的不安全行为是错误估计了发生危险的可能性；许正权等[4]通过构建矿工行为状态空间模型，得出矿工的不安全行为可能会被其他矿工学习模仿。矿工无意间产生的不安全行为较少，通常是低估风险或为减轻工作量而有意采取不安全行为，而这种有意识的行为更容易被模仿[5-6]。因此，减少矿工对不安全行为的模仿，降低不安全行为的传播率，就可以降低煤矿事故的发生概率。在研究行为传播时，最初使用的是基于流行病传播的SIR、SIRS 等模型[7]，这些模型将矿工分为3 类：易染矿工、不安全矿工和免疫矿工，并假设这3 类矿工按照易染、不安全、免疫的顺序逐次转化。但现实中矿工的分类更加细化，各类矿工之间会相互转化，行为传播过程也更复杂。为此，通过增加潜伏矿工这一分类，构建了新SEIRS 模型来研究各转化率对不安全行为传播的影响，确定影响最大的转化率及传播阶段，从而更有针对性地管理矿工间不安全行为的传播。

1 矿工不安全行为传播模型的构建

1.1 模型可行性分析

根据行为传播[8]理论，矿工不安全行为会被传播。当煤矿区队中存在1 个或多个不安全作业的矿工时，若其余矿工安全意识薄弱且煤矿安全管理不到位，不安全行为便会大规模传播。这种传播具有传染性、改正性和反复性，与流行病传播过程中的传染、治愈、免疫及丧失免疫的特点相似[9]。因此，通过建立流行病传播动力学方程来研究矿工间不安全行为的传播是可行的。

1.2 模型构建

将矿工分为4 类：易染矿工（Susceptible Miner）、潜伏矿工（Exposed Miner）、不安全矿工（Infected Miner）和免疫矿工（Recovered Miner）。 易染矿工是指处于安全生产状态，但易受影响而产生不安全行为的矿工；潜伏矿工是指虽在安全生产，但有冒险意识并认同不安全行为，将来可能转化为不安全矿工的群体；不安全矿工是指进行不安全操作并会将自身不安全行为传播给其余矿工的人群[10]；免疫矿工是指不安全矿工经过安全教育或自我反省，意识到错误从而不再进行不安全操作的矿工。

传统SEIRS 模型只考虑4 类矿工依次转化的情况。但由于矿工个性特质不同，风险厌恶型矿工可能先转化为潜伏矿工，而风险偏好型矿工可能直接转化为不安全矿工。因此，扩展传统模型，假设易染矿工会转化为潜伏、不安全和免疫矿工。当区队内的不安全矿工被处罚后，大部分矿工转化为免疫矿工，区队不安全行为大幅减少。免疫矿工虽然处在暂时免疫状态，但若长期未经教育监督，部分免疫矿工便会转化为易染矿工。通常煤矿区队在一个动态演化周期内，人数不会发生变化，因此，该模型假设矿工总人数不变。模型的传播过程如图1。

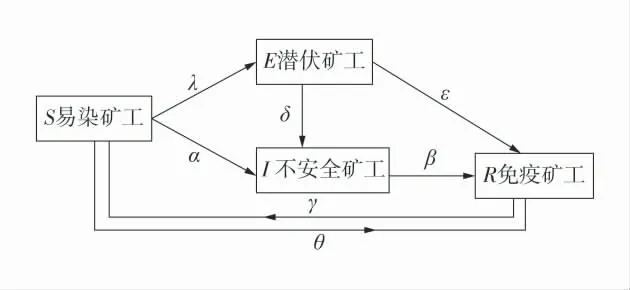
图1 新SEIRS 不安全行为传播模型Fig.1 New SEIRS unsafe behavior propagation model

1）S→E。易染矿工受不安全矿工影响，以λ 的概率转化为潜伏矿工，λ 为易染矿工的潜伏率。

2）S→I。易染矿工受不安全矿工影响，以α 的概率转化为不安全矿工，α 为易染矿工的传染率。

3）E→I。潜伏矿工未经安全教育，以δ 的概率转化为不安全矿工，δ 为潜伏矿工的转化率。

图4表明，压实膨润土混合物浸水后发生显著的膨胀，纯膨润土的膨胀率为157%；当同时添加纳米氧化钙(4%)和纳米氧化硅(6%)后，其膨胀率依然高达170%。

4）E→R。潜伏矿工受到良好的安全教育，以ε的概率转化为免疫矿工，ε 为潜伏矿工的矫正率。

5）I→R。不安全矿工因受到安全教育或自我反省等原因以β 的概率转化为免疫矿工，β 为不安全矿工的治愈率。

6）S→R。易染矿工因风险厌恶等原因以θ 的概率转化为免疫矿工，θ 为易染矿工的免疫率。

7）R→S。长期缺乏教育监督的免疫矿工以γ 的概率转化为易染矿工，γ 为免疫矿工的遗忘率。

根据上述传播过程，建立微分方程组如下：

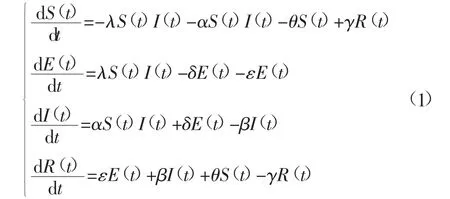
式中：S（t）、E（t）、I（t）、R（t）分别为t 时刻易染矿工、潜伏矿工、不安全矿工和免疫矿工占全体矿工的比例；λ、α、δ、ε、β、θ、γ 分别为潜伏率、传染率、转化率、矫正率、治愈率、免疫率和遗忘率；S（t）、E（t）、I（t）、R（t）为关于t 的连续可微、值域为［0，1］的函数，且λ、α、δ、ε、β、θ、γ 的取值范围均为［0，1］。

当系统处于平衡时，将2 组平衡点分别记为M0（S0，E0，I0，R0）和M*（S*，E*，I*，R*）。M0（S0，E0，I0，R0）是系统的无传播平衡点，此时煤矿区队内没有任何不安全行为，为理想状态。当区队中存在不安全矿工且传播不安全行为时，系统平衡点为M*（S*，E*，I*，R*）。

2 矿工不安全行为传播的系统仿真

式（1）所示的微分方程组无解析解，可以通过数值模拟的方法，基于Python 进行数值仿真分析4类矿工的数量变化情况。假设1 个煤矿区队人数为100 人，1 个不安全行为的传播周期为60 d。该模型假设易染矿工的初始密度为0.99，不安全矿工的初始密度为0.01，潜伏矿工和免疫矿工的初始密度均为0。

根据模型仿真结果得出：传播初期易染矿工的数量S′（t）迅速下降，若不采取任何措施，易染矿工迅速向其他3 类人群转化；潜伏矿工的数量E′（t）初期有少量增加，但在整个传播周期内非常稳定；不安全矿工的数量I′（t）初期不断增加，在第18 d 以后增加的趋势平缓，最终达到稳定状态；免疫矿工的数量R′（t）在初期增加较为迅速，最后密度保持不变，系统达到相对稳定状态；易染矿工、潜伏矿工、不安全矿工与免疫矿工分别约在第26 d、第15 d、第22 d 和第23 d 达到稳定状态。

3 系统稳态分析

采用控制变量法，改变某一转化率并研究其变化对4 类矿工变化趋势及稳态影响。各转化率初始值为α=0.5，β=0.2，λ=0.4，δ=0.5，ε=0.5，θ=0.1，γ=0.2。

3.1 易染矿工的转化率对系统稳态的影响

不同传染率α、潜伏率λ 和免疫率θ 下，4 类矿工数量的变化趋势如图2。

由图2 可知：

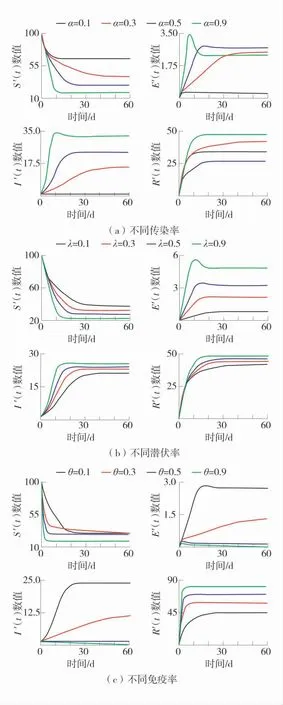
图2 不同情况下4 类矿工数量的变化趋势Fig.2 The changing trend of the number of four kinds of miners under different conditions

1）当α 越大，易染矿工的数量S′（t）下降越快，稳态人数越少。α 为0.1 和0.9 时，易染矿工最终分别稳定于70 人和20 人。同时，当α 为0.9 时，稳态下免疫矿工的数量R′（t）达到最大值48 人。α 越大，不安全矿工的数量I′（t）增加越快，稳态下数量越多。因此，α对系统稳态产生较大影响。

2）λ 增加，易染矿工的数量S′（t）下降越快，稳态下数量更少。当λ 为0.1 和0.9 时，易染矿工最终分别稳定于40 人和20 人，潜伏矿工最终分别稳定于0.5 和5。随着λ 增大潜伏矿工的稳定人数少量增加，同时导致不安全矿工的数量I′（t）和免疫矿工的数量R′（t）增加得更快，且稳态下数量更多。

3）当θ 为0.1 和0.9 时，易染矿工最终分别稳定于30 人和20 人。θ 增加，潜伏矿工的数量E′（t）减少且不安全矿工的数量I′（t）增加得更慢，而免疫矿工的数量R′（t）增加得更快。当θ 为0.5 和0.9 时，潜伏矿工和不安全矿工的稳定数量几乎趋于零。当θ取0.1 和0.9 时，免疫矿工最终分别稳定于40 人和80 人。

3.2 潜伏矿工的转化率对系统稳态的影响

4 类矿工数量在不同转化率δ 和矫正率ε 下的变化为：

1）δ 增高，易染矿工的数量S′（t）下降得更快，稳态下易染矿工数量更少。δ 为0.1 和0.9 时，易染矿工分别稳定于40 人和30 人。δ 增高导致不安全矿工的数量I′（t）与免疫矿工的数量R′（t）增加得更快，稳态下不安全矿工数量更多，且更早达到稳定状态。

2）ε 增高，易染矿工的数量S′（t）下降得更慢，且最终稳态下数量更多。ε 为0.1 时，易染矿工最终稳定于24 人，ε 为0.9 时，易染矿工最终稳定于35人。ε 越大，潜伏矿工的数量E′（t）上升越慢。ε 越小，不安全矿工的数量I′（t）越大。ε 对免疫矿工数量没有太大的影响，无论ε 取值如何，最终R′（t）均稳定于42 人左右。

3.3 不安全矿工的转化率对系统稳态的影响

4 类矿工的数量在不同治愈率β 下的变化情况如图3。

图3 4 类矿工的数量在不同治愈率β 下的变化情况Fig.3 Changes in the number of Type 4 miners with different cure rates

由图3 可知，β 增高，易染矿工的数量S′（t）下降得更慢，稳态下易染矿工数量更多。β 为0.1 时，易染矿工最终稳定于14 人；β 为0.9 时，易染矿工最终稳定于66 人。β 的改变对易染矿工数量S′（t）影响显著。β 增高，不安全矿工的数量I′（t）下降得更快，β 为0.5 和0.9 时，稳态下潜伏矿工的数量E′（t）和不安全矿工的数量I′（t）几乎都为0，由此得出β对稳态下潜伏矿工的数量与不安全矿工的数量没有显著影响。当β 为0.3 和0.5 时，稳态下免疫矿工的数量R′（t）最终稳定在32 人。

3.4 免疫矿工的转化率对系统稳态的影响

4 类矿工数量在不同遗忘率γ 下的变化情况：γ对易染矿工的数量S′（t）没有显著影响，无论γ 值如何改变，易染矿工最终均稳定于30 人。γ 增高，潜伏矿工的数量E′（t）增加。当γ 为0.1 和0.9 时，潜伏矿工稳定数量分别为1.3 和5.6。γ 越大，不安全矿工的数量I′（t）增加得越快。当γ 为0.1 和0.9 时，不安全矿工最终分别稳定于11.6 和48.8。另外，γ 越大，最终稳态下免疫矿工的数量R′（t）越少。当γ 为0.1 和0.9 时，免疫矿工数量分别稳定于58.5 和17。

3.5 结果讨论

研究了不同转化率对稳态下各类矿工数量的影响。转化率变化对4 类矿工数量的影响见表1。其中，↑表示明显的正相关，↓表示明显的负相关，-表示不能明显显示出正负相关的情况。

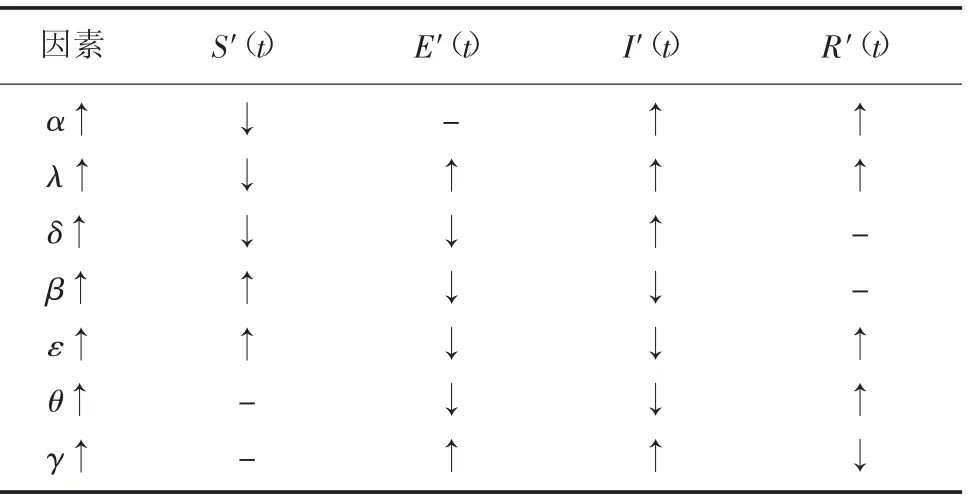
表1 转化率对4 类人群数量的影响Table 1 The impact of the conversion rate value on the number of four types of people

实验中，传染率α、潜伏率λ、转化率δ 和遗忘率γ 与不安全矿工的稳态数量呈正相关，治愈率β、矫正率ε 和免疫率θ 与不安全矿工稳态数量呈负相关。

在煤矿工作中，采取不安全行为并将其不良行为进行传播的矿工对煤矿安全影响最大，因此分析各转化率对不安全矿工的影响就能有代表性地分析煤矿区队的不安全程度。不安全矿工数量对各转化率的敏感性分析结果：α 为15.1%，λ 为16.6%，δ 为12.5%，β 为－11.2%，ε 为－12.5%，θ 为－19.4%，γ 为12.7%。转化率的取值范围均为［0.3，0.5］。

对不安全矿工稳态数量影响最大的转化率是免疫率θ，其次是潜伏率λ 和传染率α。θ、λ 与α 分别是易染矿工对于免疫矿工、潜伏矿工和不安全矿工的转化率。根据上述结论可知，易染矿工的转化方向对煤矿间不安全行为的传播最为重要，在4 类矿工群体中处于关键地位。因此，在煤矿管理中，必须重视易染矿工的转化方向，尽可能提高免疫率，进而降低稳态下不安全矿工的数量，将不安全行为控制在最小范围以达到安全管理的目标。

4 结 语

为减少不安全操作的人数，首先应考虑的是提升易染矿工的免疫率，其次是降低潜伏率与转化率。易染矿工的转化方向是影响煤矿区队安全程度的重要因素。为减少煤矿不安全行为，同时将不安全矿工的人数控制在最小范围，应着重加强对新员工的安全教育培训与监督管理，从而增加易染矿工转化为免疫矿工的概率。通过构建新SEIRS 模型及Python 仿真得出，矿工间不安全行为的传播存在一定规律性。应努力认识和掌控其规律，并针对性开展煤矿、区队安全培训及安全管理。