基于CATIA二次开发的无人直升机油箱优化方法
2022-06-22王泽玉
米 雪,王泽玉
(中国直升机设计研究所,江西 景德镇 333001)
0 引言
直升机燃油质量特性是指直升机所载燃油在不同飞行姿态下的油量、重心、惯性矩、惯性积等特征,对直升机燃油系统设计方案的可行性判定及飞机在飞行过程中改善飞行品质、保证飞行安全具有重要意义。直升机燃油箱外形设计的好坏,将直接影响直升机燃油质量特性,对全机重心评估及控制具有重要影响。
现代中小型无人直升机通常将油箱布置在旋翼下方,并采用整体式结构油箱。其内部安装有形状各异的管道、泵、阀等部件,结构越来越复杂。设计者在进行复杂结构燃油箱设计时,不会考虑油箱结构对重心波动影响的情况。这是由于采用传统手动分割油箱方法计算燃油重心的计算效率极低,难以满足对整个油箱的质量特性分析的需求,无法为油箱结构优化设计提供指导。
本文采用CATIA二次开发技术,提出了一种基于瞬态工况的燃油重心计算方法,可对无人直升机各个飞行工况下的燃油重心进行计算,并设计多种油箱方案,对比不同油箱方案在瞬态工况下的重心变化情况,得出最优的油箱设计方案,对油箱结构设计提供优化方向。
1 动态燃油体建模
1.1 燃油体定义
油箱实体是指油箱内部包络形成的整个空间;燃油体是指液体燃油在燃油箱内所形成的形状,即燃油平面和油箱侧面、油箱底面之间形成的几何体空间,如图1所示。本文以燃油体作为重心分析对象,根据实际使用的燃油类型,指定不同的燃油密度,通过CATIA自带的分析模块来获取燃油的重量重心特性。为了方便计算,本文选取机体坐标系作为参考坐标系,如图2所示,以直升机旋翼轴底端作为坐标原点,轴平行于直升机纵轴指向机尾,轴平行于直升机横轴指向右方,轴平行于直升机竖轴指向机身上方。
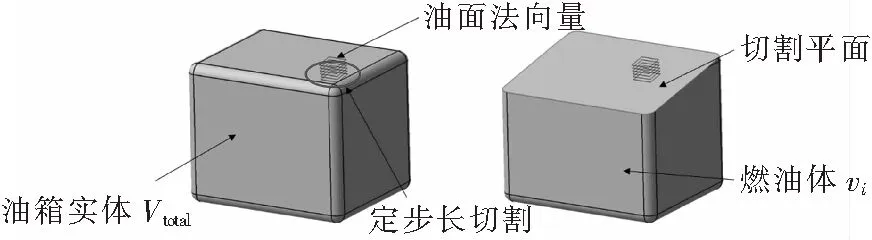
图1 燃油体定义
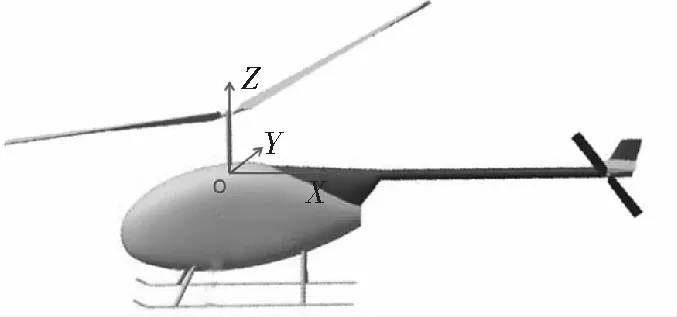
图2 机体坐标系
1.2 瞬态燃油平面计算
油面法向量是处理燃油体及计算燃油体质量特性的重要依据,由无人直升机飞行姿态和飞行过载共同确定。本文依据文献[5]中提供的方法,计算油面法向量:
=cos-sin
(1)
=(sin+cos)sin+cos
(2)
=(sin+cos)cos-sin
(3)
式中:(,,)为机体坐标下的油面法向量;(,,)为地面坐标系下的过载系数矢量;为直升机的俯仰角;为直升机的滚转角。
在油箱形状一定、油面法向量已知的情况下,燃油平面仅与油箱内剩余燃油量有关。燃油平面的平面方程为:
++=
(4)
=++
(5)
使用燃油平面(即切割平面)切割油箱实体,即可获得燃油体(如图1)。
1.3 无人直升机飞行工况设计
飞行剖面是指为完成某一特定飞行任务而绘制的飞行航迹图,对于无人直升机而言,通常包括:垂直爬升、悬停、平飞、下滑等。本文依据某型无人直升机飞行的典型任务剖面(如图3所示),选取11个典型工况点的飞行试验数据,得到该型机在不同工况点时三个方向的过载系数、俯仰角、滚转角和剩余燃油量(见图4),数值如表1所示。
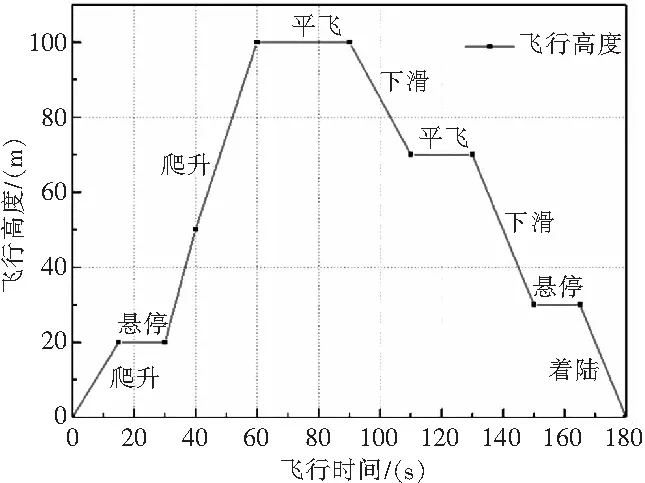
图3 某飞行剖面图
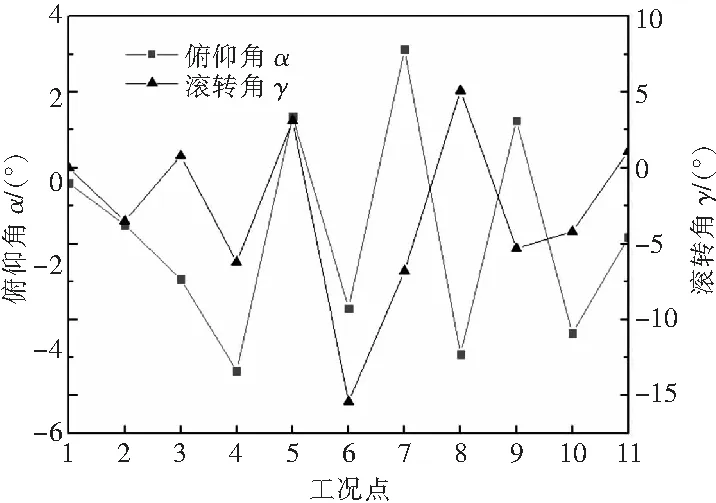
图4 选取部分工况点
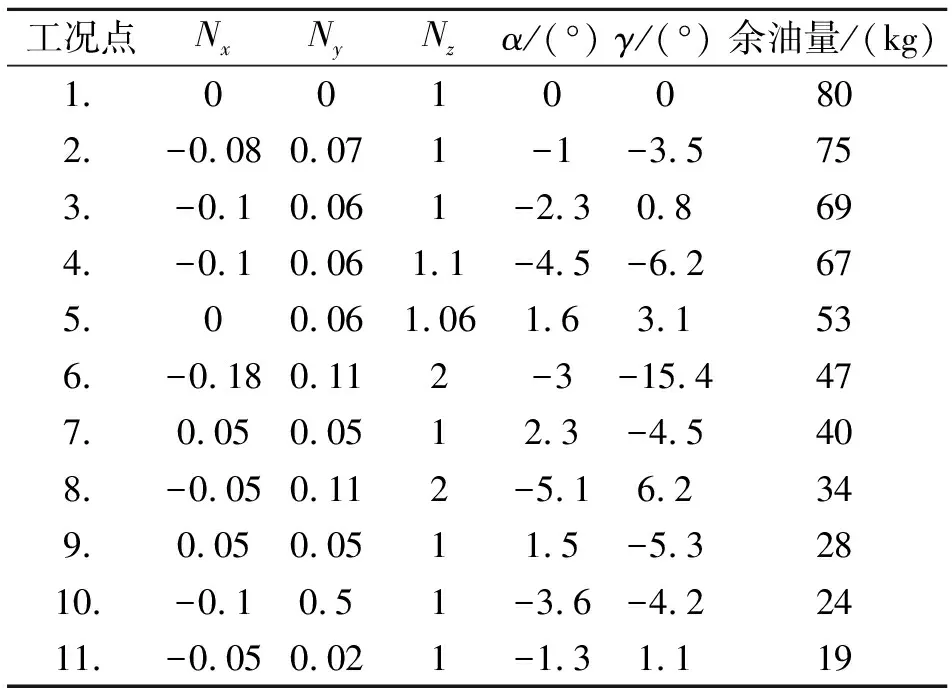
表1 飞行工况点下的飞行参数
2 基于CATIA二次开发的瞬态工况燃油重心计算方法
为获取瞬态工况下燃油体的重量重心数据,本文通过CATIA V5 Automation API 二次开发接口,使用 Visual Basic 语言,依据飞行工况数据,对燃油体数模进行分割和燃油质量特性计算。首先基于油箱创建Measurable对象,通过读取飞行状态确定油面法向量,结合余油量对油箱实体进行分割;最后基于分割后的燃油体创建Inertia对象,从而得到燃油体的重量及重心。具体流程图5所示。
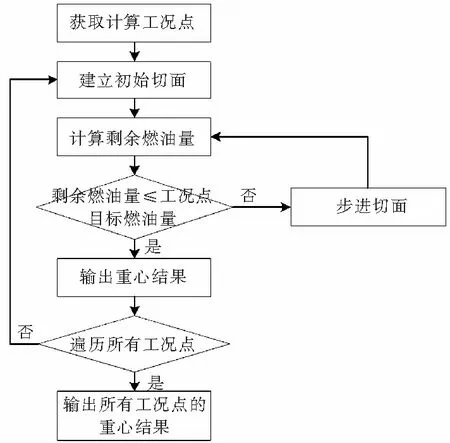
图5 燃油重心计算流程图
2.1 初始条件设定
首先按照表1中11个工况点,计算燃油平面法向量(,,),如表2所示;使用Visual Basic读取表格中的燃油平面法向量,作为计算的初始条件。燃油平面初始高度设置为油箱顶面以上的一个高度,以确保最优值不被忽略。
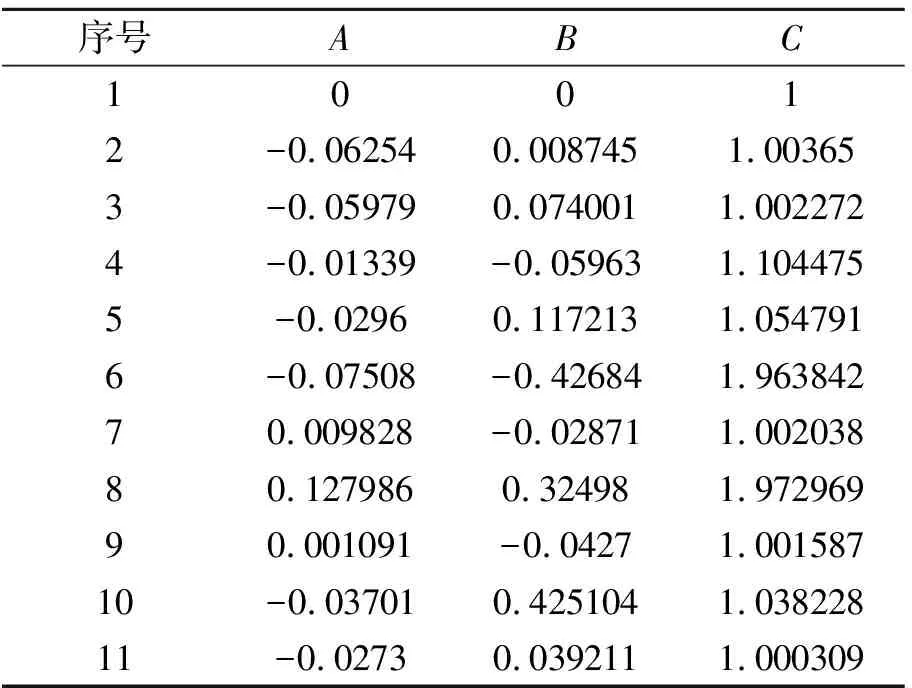
表2 飞行工况点对应燃油平面参数
2.2 燃油实体分割
要获得某工况的燃油体,除确定油面法向量(,,)外,还需要根据该工况的剩余燃油量确定油面高度。本文采用定步长方法,以油箱顶部某一高度作为初始位置,从满油状态开始定步长切割燃油体,直至剩余燃油体质量小于等于目标工况质量,则结束循环。切割后的燃油实体,即为当前工况下的机上燃油形态。
针对同一油箱实体,分别采用10 mm、5 mm和2 mm的步长进行计算,得到计算燃油质量、误差和计算次数如图6和表3所示。
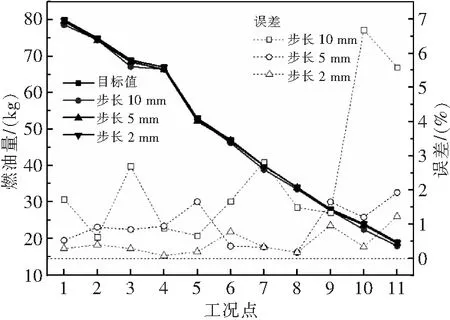
图6 不同计算步长时各工况点的燃油质量及误差

表3 步长计算误差及次数
由图6和表3可以看出,计算步长为5 mm和2 mm时,燃油质量曲线基本与目标值一致,最大误差分别为1.66%和0.96%,均在2%以内,且2 mm计算步长时的计算次数为5 mm时的2.43倍。为保证计算精度同时节省计算时间,最终选用5 mm作为燃油质量计算步长。
2.3 燃油重量重心获取
通过CATIA VBA中的GetTechnologicalObject功能和GetCOGPosition,分别读取燃油体的重量、重心数据,并保存记录。关键代码如图7所示。

图7 获取燃油体对应重量重心的关键代码
通过上述步骤,即可获得无人直升机瞬态工况下的重心变化情况。本文设计软件界面如图8所示。本文以此作为油箱形状优化的依据。
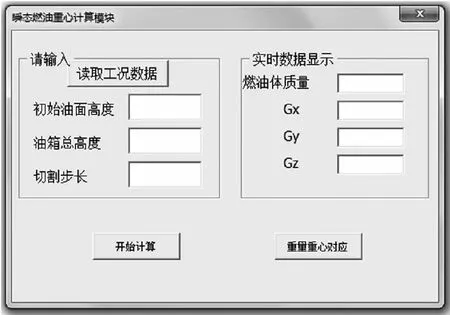
图8 重心计算软件界面
3 油箱优化分析
3.1 规则油箱计算分析
无人直升机燃油箱通常布置在旋翼下方,直升机全机重心位置附近。燃油箱在设计时,应尽量保持无人直升机重心稳定。本文选取图9(a)-(d)所示的4种界面连续变化的油箱形状作为分析对象:(a)油箱为规则的长方体形;(b)油箱沿方向前后窄、中间宽;(c)油箱沿方向上窄下宽;(d)油箱沿方向上宽下窄。设定4种油箱高度一致,体积相同,且油箱满油状态时相同,均为0,依此展开油箱重心分析。
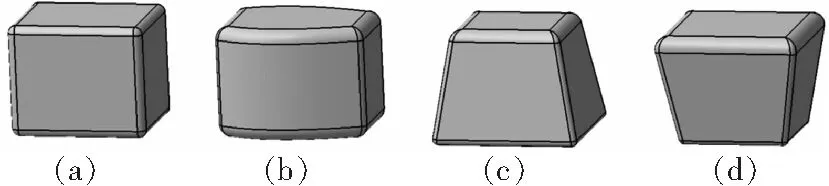
图9 油箱方案设计
依据1.3节中的11个瞬态工况点,本文对图7中四种油箱、方向重心进行计算,得到结果如图10所示。其中图10(a)为方向重心变化情况;图10(b)为方向重心变化情况。

图10 四种油箱重心变化情况
由图10可以看出,第8个工况点时,方向重心偏移最大,为1.3 mm;第10个工况点时,方向重心偏移最大,为8.3 mm。当油箱内燃油量占总量的90%~80%以及30%以下时,重心变化情况受油箱形状影响较大;而燃油量处于90%以上以及80%~30%之间时,重心变化情况受油箱形状影响较小,主要受飞行过载及飞行姿态的影响。以上规律仅适用于界面连续变化的单个油箱,当截面存在突变或多个子油箱时,应另行讨论。油箱(d)因其上宽下窄的结构特点,在前几个工况点,燃油量较多时,变动明显较大,而当燃油量消耗到30%以下时,该油箱重心变化范围相对缩小。
为更直观地体现不同燃油箱燃油重心的变动情况,本文对四个油箱的燃油重心标准差、进行计算,计算公式如下:
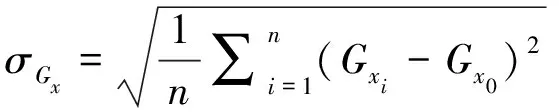
(6)
同理。式中,为状态点数,为油箱满油时的重心初始位置。计算结果如表4所示。
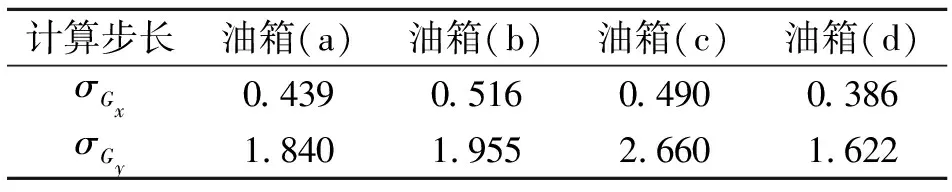
表4 不同油箱的重心位置标准差
由表4可以看出,在本文中设定的11个工况点条件下,油箱(d)的重心在方向和方向变化均为最小,即为最优方案。而在实际使用过程中,依据无人直升机的性能特点、典型工况,选取足够数量的工况点样本,使用本文中描述的优化方法,即可找到最优的燃油箱形状设计方案。另一方面,对于已完成设计的燃油箱,也可以使用本文中的方法分析油箱质量特性及重心变化范围,从而评估整机重心。
3.2 实际油箱计算及分析
依据本文所述方法,对某两型无人直升机燃油箱进行计算分析,油箱形状如图11所示。燃油箱A形状较为简单,单侧油箱近似为长方体,且关于轴对称;燃油箱B为马鞍形,且内侧结构较为复杂。得到方向重心计算结果如图12所示。
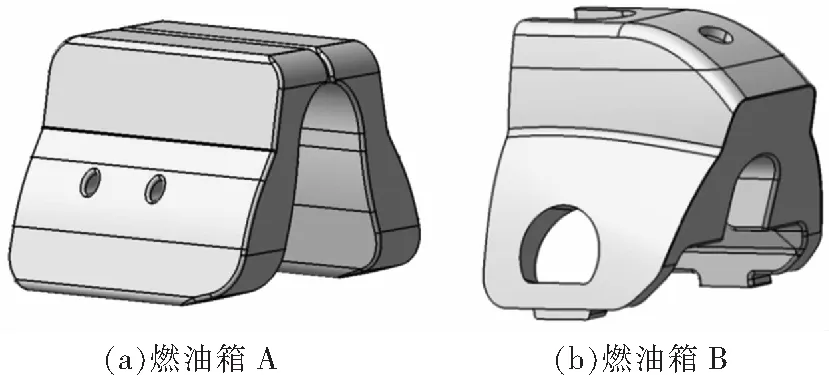
图11 某两型无人直升机燃油箱对比
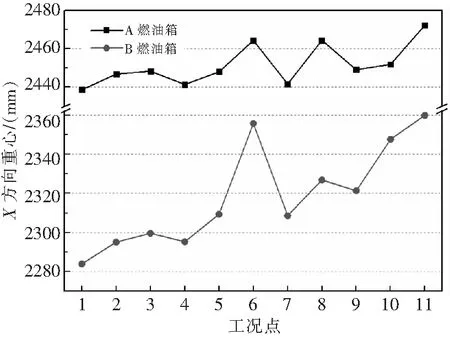
图12 某两型无人直升机重心变化情况对比
可以看出,两个油箱重心特性差异明显:在相同工况下,油箱A重心变化范围为33 mm;油箱B重心变化范围为76 mm。从飞行稳定性的角度而言,油箱A明显优于油箱B。油箱B顶端空腔占比较大,下端空间较小,在满油状态下,重心稳定性相对较好;燃油量低于30 kg后,重心受飞行姿态影响尤其明显。在油箱结构设计过程中,应尽量保持75%以下燃油量的重心稳定性;75%以上空间使用率相对较低,这部分可根据机体结构需要设计为异形结构。
4 结论
本文基于CATIA二次开发技术,提出了一种根据过载、飞行姿态和余油量自动计算瞬态燃油重心的方法;
本文验证了不同油箱切割步长的计算精度,证明以5 mm作为定步长切割,既可以保证计算精度,又能节省计算时间;
依据本文的瞬态工况燃油重心计算方法,得出相同工况下四个理论油箱和两个实际油箱的重心变动情况,并加以分析给出优化建议;
本文提出的优化方法不仅可以在设计阶段提供优化方向,也可用于已知油箱的质量特性计算、油量传感器标定及全机重心评估。
