高速铁路乘务计划新旧交替方案编制

刘仁华 代潇斌 莫逸佳 赫富静

摘要：随着我国高速路网的不断完善，需经常调整铁路运行图，同时也需要协同更新乘务计划，以应对列车运行图调整后出现的新要求。本论述设计了不同交路类型间交替的接续权值，表示新旧乘务计划之间接续的评价指标;建立了二元整数规划模型将新旧乘务排班交替问题转化为二维指派问题，采用 LINGO 求解器对较大规模的乘务计划算例进行求解。算例求解结果验证了本论述模型与算法的可行性，提高了新乘务计划编制的质量。

关键词：乘务计划;新旧交替;LINGO

中图分类号：U24                                             文献标志码：A

0 引言

铁路乘务排班计划问题是我国高铁运营管理的重要问题之一，乘务排班计划的优劣会直接影响到高速铁路的运营与经济效益。为了适应铁路客流波动，提供与之匹配的客运服务，我国近几年每年都要多次对列车运行图与乘务计划进行协同调整。在乘务计划调整中新的乘务计划往往不会与旧的乘务计划很好的接续。为了优化乘务计划的编制流程，提高乘务计划的编制质量，国内外对各类问题进行了大量研究。

现有文献中，国内外的研究人员在优化乘务计划编制和编制方法方面做了很多研究，获得了许多成果。田志强[1 ]详细地研究了乘务计划的特征，建立乘务计划总成本最小的集合覆盖模型，采用多种启发式算法对模型进行求解。赵鹏[2 ]对各种运输方式的乘务计划编制的研究进行了统筹规划，实现了乘务计划的自动化编制。冉婧入[3]把该问题划为两个子问题，通过蚁群算法和贪婪算法分别对计算机与手工编制客运乘务计划进行优化。曾子凌[4 ]根据中国高铁的特征，设计了乘务计划调整模型和高铁一体化动车组的运用计划。杨国元等[5]根据劳务时间和交路计划为主要的约束条件，设计了以降低乘务成本，减少一次工作所需乘务员数量为目标的乘务计划编制模型，采用遗传算法进行求解该问题。R Freling [6]建立了乘务员调度问题的框架，并根据实际问题设计了一种启发式算法，以求解大规模的乘务调度问题。M Fuentes[7 ]针对距离不大但服务频率很高的快速交通网络，提出了能够从线性支付政策中受益，并使其更容易与其他规划问题集成的新方式去解决乘务员调度问题。林枫[8]将乘务计划编制过程分为两个阶段，分别优化了接续时间与乘务员过夜次数，设计了 MOMS 求解算法对模型进行求解。周凌霜等[9]研究了当动车组运用计划调整后协同调整乘务计划，最小化了列车运行线的取消数量和偏移量。

现有文献对于铁路乘务排班的研究有两个主要方向，一是将乘务排班计划规则引入时空网络，采用求解最短路的方法，求解乘务排班的最优方案;一是采用多种启发式或精确求解算法对大规模的乘务排班方案进行优化。较少有文献对乘务排班方案随着列车运行图调整对应变化时，对新旧乘务排班方案接续质量的优化进行研究。

本论述的研究内容就是减少新旧乘务计划的交替对铁路运输造成的影响，降低交替带来的额外费用，并尽可能地实现新旧乘务计划的无缝衔接，确保乘务员能够更好的执行新乘务计划。

2 乘务排班计划模型建立及算法设计

2.1 相关概念

值乘区段：乘务人员能够一直担当值乘任务的最小区段叫做值乘区段。乘务交路：乘务员（组）从乘务基地出发到返回乘务基地，担当值乘任务的全部流程。乘务排班计划：安排乘务组在一个乘务周期内的出乘、值乘、换乘和退乘的具体方案，它能够决定在该乘务周期内所需要的乘务员数量。

2.2 乘务计划编制的依据

乘务排班计划是安排乘务组在一个乘务周期内的出乘、值乘、换乘和退乘的具体方案。乘务计划编制的成果会直接影响到乘务员的值乘，从而最终影响到旅客对铁路运输服务的评价。表1 为某客运段的一部分客运乘务交路表。

2.3 新旧乘务排班计划交替分析

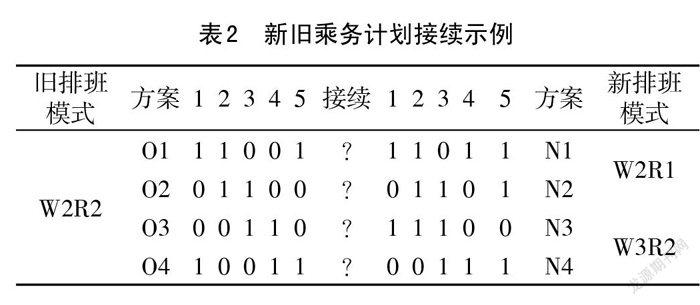
当列车运行图发生变化时，乘务计划也一定需要重新编制或者进行调整，即需要进行乘务计划的交替。此时如何使乘务计划交替对乘务员（组）乃至对铁路所带来的影响降到最低，是铁路编制乘务计划的技术人员要考虑的重要问题。乘务计划的交替最有可能出现的是新旧乘务计划的交路类型发生了变化，如 W2R2交路（工作两天休息两天模式的交路模式）可能需要接续 W3R交路（工作三天休息两天模式的交路模式）。為了让交替带来的影响降到最低，本论述需要对执行 W2R2交路的乘务员与新计划中的 W3R2交路进行优化配对。尽量做到乘务员以休息（工作）结束旧计划，以工作（休息）开始新计划，这样做的目的是平衡过渡乘务计划，降低乘务员对新计划的不适，使乘务计划交替的结果尽可能的达到最优。新旧乘务计划接续示例见表2 所列。

左边为旧的排班计划编制周期倒数后5 d，右边为新排班计划的前5 d，表中0 表示休息，1表示工作。对于上表这样的乘务计划交替，要想达到预期的结果，就必须做好不同乘务计划的配对问题。如表中旧计划的O4若接续新旧划中的 N3，就是不合理的。因为这样接续会使原来执行旧计划 O4的乘务员在旧计划中值乘两天后还要继续在新计划中值乘三天，即这个乘务员需要连续担当五天的值乘任务，不能达到本论述预期中的使乘务计划平稳交替的结果，且乘务员若是连续担当过长的值乘任务，会导致该乘务员的值乘能力下降，最终会影响铁路的服务质量，降低人们对铁路出行服务的评价。

2.4 新旧乘务排班方案接续权值设计及计算

乘务计划的交替主要是其交路类型的变化。若乘务交路的类型发生了变化，在新旧方案进行交替时，很容易会出现不能兼顾到所有的乘务员（组）情况。如果新旧乘务计划中均包含较多的乘务排班方案，一个乘务员（组）在乘务计划交替期间出现连续值乘的概率将会增加。此外，乘务计划在更新时，也会出现新旧交路需要的乘务人员数的不同。如果人数由少变多，按照本论述的求解方式求解接续权值最小的新旧交替方案即可，没有人员担当的新交路，采用抽调的额外乘务员来完成。如果人数由多变少，将原有乘务员的任务与新任务进行匹配，抽调的额外乘务员不执行任务。本论述将乘务员划分为两类，一类是熟悉高速动车组列车上的值乘任务;另一类是熟悉普速动车组列车的值乘任务。出于对服务质量的考虑，本论述优先考虑安排符合条件的乘务员（组）。

为了更好的体现乘务员的类型变化，知道排班模式是否包含高速动车组值乘任务，乘务员的工作是否需要或者能够担当高速动车组值乘任务。本论述需要建立一个对应关系，即原本执行旧排班方案的乘务员，其本身熟悉的列车类型是什么样的。而乘务员是否熟悉该种列车的工作环境，会对铁路的服务质量产生影响。本论述通过设计一种乘务方案接续权值来直观的评价乘务计划交替结果好坏。

为了能够更好的衡量旧排班方案向新排班方案衔接过渡的优劣程度，设计如下变量：

Oi 为旧排班方案，共有 m 个旧排班方案;Nj 为新排班方案，共有 n 个新排班方案;旧排班方案结束时的连续工作日用 w i（O）表示;旧排班方案结束时的连续休息日用 r i（O）表示;新排班方案开始时的连续工作日用wj（N）表示;新排班方案开始时的连续休息日用rjN表示;WiO为旧排班方案的连续工作时间标准;R i（O）为旧排班方案的连续休息时间标准;WiN为新排班方案的连续工作时间标准;R i（N）新排班方案的连续休息时间标准;

新旧乘务排班方案的接续权值的设计与计算方法如下：

（1 ）新旧排班方案接续合理性指标θij（c）

（2 ）排班模式相异性指标θij（p）

为了使乘务员从旧排班方案结束后更为顺利的转入新排班方案，式（7）定义了排班模式相异度指标，用以体现新旧排班模式之间的差异，并设计其计算公式

如下：

新旧排班方案接续合理性指标与新旧排班模式相异性指标之和，为排班方案接续的最终权值，如式（8） 所示。

在接续权值的设计中加入乘务员担当值乘任务的列车类型变化的情况。列车类型 D 表示该方案需要乘务员在普速动车组列车（D 字头）上担当值乘任务。列车类型 G 表示该方案需要乘务员在高速动车组列车（G 字头）上担当值乘任务。本论述在接续权值中如（9）～ （12）所示：

D 类型列车乘务员接续 D 类型列车乘务计划：

不同乘务员类型之间接续通过一个比1 大的系数，弥补担当不同乘务任务的乘务员之间接续的损失值由此可得到 D 类型乘务员接续 G 类型列车乘务计划：

G 类型列车乘务员接续D 类型列车乘务计划：

（11）

G 类型列车乘务员接续 G 类型列车乘务计划：

（12）

θij终就是本设计的乘务计划新旧交替的最终接续权值。它基本能够满足上述中提到的所有的要求。通过接续权值的设计与计算将表2 的新旧乘务计划接续示例转换成下表3的形式，接续权值计算结果见表4 所列。

2.5 乘务计划接续的优化模型及算法

本论述研究的模型为0 ～1 整数规划模型，式（13） 为乘务接续的优化目标值，旧乘务排班方案数量为 m ，新乘务排班方案数量为 n ，k=maxm， n，aij为旧乘务排班方案 Qi  ，与新乘务排班方案 Nj  的接续权值，式（14）中xij为二元决策变量，表示旧乘务排班方案 Qi 是否能够接续新乘务排班方案 Nj   ，若能为1，否则为0。由于新旧乘务计划所包含的乘务方案的数量可能不同，因此我们加入一个虚拟的新（旧）乘务方案，使它与所有旧（新）乘务方案的接续权值均为0 。本论述设计的模型属于线性模型，将新旧乘务计划的接续问题化为二维指派问题，将接续权值看作指派问题中的“费用”可以直接采用 LINGO 软件求解该问题。最终求出来的乘务计划新旧交替方案见表6 所列。

3 算例分析

为了证明本文所设计的算法能够快速编制一个合理的、可行的乘务计划新旧交替方案，使得该算法可以在实际乘务计划交替时使用。本章将采用某局某客运段乘务计划交替时期新旧乘务计划数据为，表5 所列为其对应的接续权值对应的矩阵表，用本论述设计的算法来计算其交替方案。

从表6 中可以看到，在计算出来的乘务计划新旧交替方案中，虚拟的旧乘务方案20与新乘务方案6 相接续，而其余的各个旧乘务方案都有接续的新乘务方案，最优接续权值为4.5。如果新旧乘务计划所包含的乘务方案数量不同，我们只需增加几个虚拟方案，使之包含的乘务方案总数量与对应方案相同即可。

4 结束语

本论述通过建立乘务排班优化模型，引入乘务排班接续权值，优化降低了高速列车乘务计划新旧交替所带来的成本，编制出了随列车运行图调整相对应的乘务排班计划。在极大地提高了编制效率的同时，保证了列车乘务员（组）可以很好的执行乘务计划。在此研究基础上，可以加入其它约束以应对现实编制乘务计划出现的各种要求。

参考文献：

[1 ]  田志强. 高速铁路乘务计划编制优化理论与方法研究[D ].成都：西南交通大学，2011.

[2 ]  赵鹏，张迦南. 铁路动车组的运用问题研究[J]. 北京交通大学学报，2009，33（3）：6-10，16.

[3]  冉婧入. 城市轨道交通 PPP 项目经济风险分析及规避风险建议[J]. 城市轨道交通研究，2021，24（9）：236-237.

[4]曾子凌. 高速铁路动车组运用计划与乘务计划一体化优化调整模型与算法[D].北京：北京交通大学，2019.

[5]杨国元，史天运，张秋亮. 鐵路客运乘务排班计划编制模型及算法[J]. 北京：交通运输系统工程与信息，2016，6（4）：159-164.

[6]Freling R，Lentink R M，Odijk M A. Scheduling train crews：a case study for the Dutch Railways[M]. Erasmus UniversityRotterdam，Erasmus School of Economics（ESE），Economet⁃ric Institute，2000.

[7] Fuentes M，Cadarso L，Marin A. A hybrid model for crewscheduling in rail rapid transit networks[J]. Transportation Re⁃search Part B：Methodological，2019，125：248-265.

[8]林枫.固定区段轮乘制乘务交路计划编制模型及算法[J].铁道学报，2019，41（12）：10-18.

[9]周凌霜，彭其渊，张志博，等.高速铁路动车组运用计划与乘务计划协同调整研究[J]. 铁道运输与经济，2021，43（5）：1-7.