钻爆法施工隧道塌方风险量化评估模型及其应用

仝跃 岳瑶 黄宏伟 周应新 雷华 段晓彬

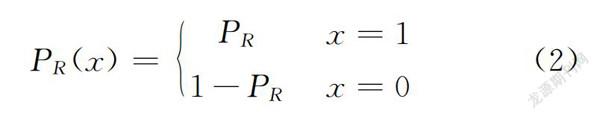
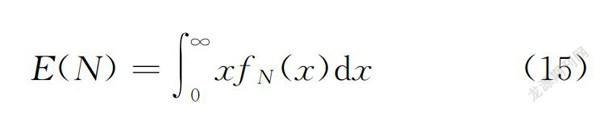
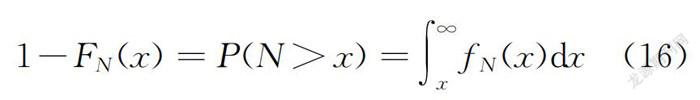
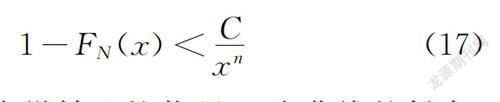
摘 要：受地質条件和施工等因素的影响，钻爆法施工中塌方事故频频出现，造成人员伤亡、机械损坏、工期延误等不良后果。目前的风险评估方法多以定性为主，难以继续满足隧道安全风险管理的需要。根据风险定义，考虑围岩物理力学参数的变异性，应用Monte-Carlo方法和数值分析实现隧道塌方发生概率的定量化分析，并基于普氏平衡拱理论实现隧道塌方规模的定量化预测;结合施工人员、机械的时空分布特征及其易损性实现人员伤亡风险、工期延误风险和经济损失风险的定量化计算;利用ALARP原则和F-N曲线建立可量化的风险接受准则，实现塌方风险的定量化评估。结合工程案例，验证了模型在隧道等地下工程塌方风险定量化评估中的适用性。

关键词：隧道工程;钻爆法;塌方;风险评估

中图分类号：U455.6 文献标志码：A 文章编号：2096-6717（2022）05-0046-11

收稿日期：2021-07-16

基金项目：云南省交通运输厅科技创新及示范项目（云交科教便[2019]36号）;云南省科技和人才平台计划（2017HC025）

作者简介：仝跃（1992- ），男，博士，主要从事隧道结构设计与安全风险研究，E-mail：tongyue2014@yeah.net。

黄宏伟（通信作者），男，教授，博士生导师，E-mail：huanghw@tongji.edu.cn。

Received：2021-07-16

Foundation items：Technological Innovationand Demonstration Project of Department of Transport of Yunnan Province （No. Yjkb [2019] No.36）; Technology and Talent Platform Scheme of Yunnan Province （No. 2017HC025）

Author brief：TONG Yue （1992- ）， PhD， main research interest： tunnel structure design， safety and risk， E-mail： tongyue2014@yeah.net.

HUANG Hongwei （corresponding author）， professor， doctorial supervisor， E-mail： huanghw@tongji.edu.cn.

Establishment and application of a quantitative assessment model of collapse risk in tunnel excavated by drilling and blasting method

TONG Yue， YUE Yao ， HUANG Hongwei， ZHOU Yingxin， LEI Hua， DUAN Xiaobin

（1. Broadvision Engineering Consultants， Kunming 650041， P. R. China; 2. Department of Geotechnical Engineering， Tongji University， Shanghai 200092， P. R. China; 3. Yunnan Communications Vocational and Technical College， Kunming 650500， P. R. China; 4. Yunnan Communications Investment & Construction Group Co.， Ltd.， Kunming 650100， P. R. China; 5. YCIC Yunling Construction Co.， Ltd.， Kunming 650041， P. R. China）

Abstract：Collapse always frequently occurs during the construction of tunnels due to the unfavorable geological conditions or other factors such as the excavation method， causing casualties， equipment damage， time delay or other adverse consequences. However， the current qualitative assessment method cannot satisfy the needs of project risk management.Hence， a novel quantitative assessment model of collapse risk is developed. Considering the variability of physical and mechanical parameters of surrounding rock， the probability of collapse is obtained by the Monte-Carlo method combined with the numerical method.The relevant zone of collapse is predicted by Protodyakonov's theory.With the predicted probability and zone of collapse， the risk of casualties， time delay and economic loss is analyzed quantitatively via introduction of spatiotemporal distribution index and vulnerability index.The quantitative assessment of collapse risk is realized by quantifiable risk acceptance criterion based on the way of ALARP principle and F-N curve.Finally， validated by engineering case history， the operability and applicability of the developed risk quantitative assessment model is illustrated.

Keywords：tunnel engineering; drilling and blasting method; collapse; risk assessment

近年来，作为重要基础设施类型之一的隧道工程发展速度和规模日益激增。然而，受地质条件、工程本身复杂性以及当前预测研究技术局限性的影响，隧道建设过程中存在着大量的不确定性因素，极易导致灾害事故的发生。其中，塌方作为隧道等地下工程建设过程中一种常见的地质灾害，会造成人员伤亡、机械损坏、工期延误等不良后果，已成为工程建设的重要安全隐患。因此，如何有效地预防或遏制隧道塌方事故的发生已成为当前隧道工程建设中亟待解决的问题。

相关研究表明，隧道等地下工程所处的岩土体性质具有显著的不确定性，主要体现在勘察钻孔之间地层分布的不确定性和岩土体参数的不确定性。这些不确定性因素的存在是塌方事故频发的根源，如何合理地对这些不确定性因素进行评价是解决隧道塌方问题的关键。风险分析作为处理不确定性因素及其带来问题的有效方法，为隧道塌方问题的解决提供了可能的途径。在此方面，Degn Eskesen等撰写了“Guidelines for Tunnelling Risk Management”，为隧道工程的安全风险管理提供了一套参照标准和方法。Xu等通过对隧道坍塌事故进行统计分析，构建多指标评估体系，对黄土隧道坍塌风险进行了分析。Ou等针对深埋隧道的塌方风险提出了一种涉及案例分析、先进地质预测、登普斯特沙弗证据理论的隧道坍塌风险分析方法。陈龙等根据统计的岩石隧道事故资料，对岩石隧道建设过程中的风险因素进行了归类，并给出了处理建议，并对风险分析方法在岩石隧道工程中的应用进行了讨论。王燕等通过对隧道塌方案例进行统计分析，总结出了塌方事故中潜在的风险因素，结合事故树分析法及层次分析法开展了风险因素的重要度和事故损失划分标准的研究。李志强等以塌方事故资料作为依据，提炼塌方事故主要致灾因子及其发生频率，计算各风险因素的客观权重，构建权重矩阵与隶属度矩阵，开展了浅埋大断面隧道塌方风险评估研究。李燕等通过构建多指标参数的塌方风险评价指标体系，基于熵理论可拓云模型开展了引水隧洞塌方风险评价。然而，如何定量地开展风险相关研究仍是工程安全风险管理的重要问题。

鉴于塌方事故频发于钻爆法施工的隧道中且钻爆法为当前隧道工程施工的常用方法，以钻爆法施工的山岭隧道为研究对象，基于风险量化分析理论，针对塌方事故概率、塌方潜在规模以及塌方事故导致的人员伤亡损失风险、工期延误损失风险、经济损失风险开展定量化研究，并定量化地制定风险接受准则，建立塌方风险定量化评估模型，以中国高放废物地下实验室主巷道工程为例，证明该量化模型的适用性。

1 风险量化评估原理

根据风险定义，風险包括风险事件的发生概率及其造成的损失，最常采用的表达方式为

R=P·C_R（1）

式中：R为某一风险事件;P为该风险事件的发生概率;C为该风险事件发生后造成的损失。对于风险事件的发生，用伯努利随机变量来表示：风险事件发生，x=1;风险事件不发生，x=0。对应的概率函数表示为

P（x）=P1-P x=1x=0（2）

如图1所示，基于式（1）和式（2）获得风险事件的概率和损失，结合相应的风险接受准则开展风险评价，即完成特定风险事件的风险评估。定量化风险评估包括风险事件发生概率的定量化分析、风险事件造成损失的定量化分析、风险事件等级（或可接受程度）的定量化评价。

2 塌方概率及规模预测

2.1 塌方概率

基于概率可靠度的分析方法是计算硐室围岩及结构稳定性失效概率的一种有效方法，能够定量地分析众多不确定性因素（围岩体、支护结构等物理力学参数随机性）对安全的影响。关于可靠度分析方法，当前主要有一次二阶矩法、响应面法、Monte-Carlo法、随机有限元法等。其中，以数值分析结合Monte-Carlo随机样本生成方法进行失效概率计算较为常用。

考虑围岩物理力学参数的变异性，应用Monte-Carlo方法生成符合参数分布特征的随机样本，利用所建立的数值模型进行大量的硐室开挖围岩稳定性计算，根据破坏判定条件统计近似得到塌方事故发生概率P。

P=NN（3）

式中：N为计算样本总数;N为数值计算中统计的结构破坏（以计算不收敛表征）次数。

关于计算样本数N，如式（1）所示，假设风险事件发生时服从伯努利分布，则可表示为样本X～B（1，P），进而样本均值μ=P，方差σ=P（1-P）。根据数理统计相关理论，P的矩估计量P∧=E（x）=μ=P为无偏估计。而N重伯努利试验，即二项分布X～B（N， P），其均值μ=NP，方差σ=NP（1-P）。 对应的μ=P，σ=1NP（1-P）。利用矩估计理论，P∧的变异系数为

δ∧=σ∧μ∧=1-P∧N·P∧（4）

则计算样本数N的初值可通过预设的P∧和δP∧被初步确定。若此初值满足计算精度需要，则计算样本数为N，否则需通过进一步迭代计算获得满足要求的样本数。

2.2 塌方规模

关于塌方规模，借鉴普氏（普罗托耶科诺夫）理论，认为：硐室开挖致使顶部岩体失稳，发生坍塌而形成自然拱;由于应力集中，两侧岩体逐渐破坏，导致顶部坍塌体进一步扩大而形成塌落拱，如图2所示。其中，填充区域为围岩失稳后所产生的塌落区域，2a和h分别为开挖硐室的宽和高，45°-φ/2（φ为内摩擦角）为侧面岩石的破碎面与垂直轴的夹角，2a和h为所形成的破坏拱的宽和高。

对于破坏拱高h，参考冯卫星等统计得到的对应于各级围岩的塌方高度（如表1所示），根据围岩等级进行初步确定。

基于普氏理论的塌方体体积计算公式为

V=S×L（5）

式中：V为塌方体积（Volume of Collapse）;S为塌方断面面积（Area of Collapse Section）;L为掘进进尺（Length of Each Excavation）。

3 塌方风险损失分析

3.1 人员伤亡损失

关于人员伤亡风险的分析，借鉴“球与盒子的组合问题”来描述风险事故发生时施工人员遭受不同程度的伤亡情况。其中，“球”对应于现场的施工人員，“盒子”则对应于人员的伤亡情况（死亡、重伤、轻伤）。

对于“球与盒子的组合问题”中的条件，设置为：球相同，盒子不同，允许有空盒子。即认为现场施工人员无区别（施工人员承受风险的能力相同，具有相同的易损性），人员的伤亡程度有区别，且可以存在空的区域，如图3所示。

关于人员伤亡风险的计算分析，参考Li等的研究成果，考虑现场施工人员的时间分布和空间分布，建立个人伤亡风险指标R（Risk Caused Personal Casualties），计算式为

R=P×∑（P×P×V）（6）

式中：P为风险事故发生在不同时间段的概率，此处按照现场工人的班次进行时间段划分;P为风险事故发生时人员W（Worker）处于不同影响区域S（Space）的概率，此处根据人员的伤亡程度对风险事故影响区域进行划分（Zone Ⅰ、Zone Ⅱ、Zone Ⅲ）;V为空间区域S内人员的易损性值。

根据现场施工人员的数量及分布情况，利用伯努利二项式分布求得不同伤亡程度的人员概率分布，具体表示为

p=p×C×p×（1-p）n-k

i=Ⅰ，Ⅱ，Ⅲ（7）

式中：p为k人处于i区的概率;p为施工人员数量为n的概率;n为施工人员的数量（number of workers）;C为n人中的k人处于i区;p为单个人员处于i区的概率。

3.2 工期延誤损失

塌方导致的工期延误主要是塌方体清除、塌方处加固处理所消耗的时间，工期延误风险指标R（Risk of Time Delay）为

R=P×∑（T+T）（8）

式中：T为灾害体清除时间（Time of Disaster Clean）;T为灾害区修复时间（Time of Disaster Repair）。

鉴于事故处理效率受地质条件、现场管理水平、施工队伍技术水平等多因素影响，塌方事故的处理时间具有很大的不确定性，假定塌方处理时间与其规模有较大的相关性。根据李志宏统计的塌方导致的工期延误时间（如表2所示），计算得到单位体积塌方导致的工期延误时间（均值为0.06，方差为0.01），取其均值计算塌方清除以及加固处理所消耗的时间，则

∑（T+T）≈0.06×V（9）

3.3 经济损失

塌方事件的发生会对影响区域内的施工器械造成一定损伤;而灾害体的清除及加固处理也需耗损一定的资源;同时，灾害体的处治所造成的工期延误还会导致经济成本的增加。故风险事故导致的经济损失R（Risk Caused Economic Losses）主要包括施工器械损坏费用R（Risk Caused Mechanical Damage Costs）、灾害体处治所需费用R（Risk Caused Disaster Handling Costs）、工期延误经济成本R（Risk Caused Time Delay Costs）（是指因工期延误导致的直接经济损失，主要包括工人工资、设备租赁费用、现场管理费用），表示为

R=∑（R+R+R）（10）

对于施工器械损坏费用，参照人员伤亡风险的分析，考虑时间和空间上的分布特征，建立R的计算式

R=P×∑（P×P×V×MV）（11）

式中：P、P含义与式（6）相同;P为塌方发生时施工器械M（Machinery）处于不同影响区域S（Space）的概率，对应于人员伤亡，此处是根据器械的损伤程度（严重损伤（Zone I′）、中度损伤（Zone Ⅱ′）、轻度损伤（Zone Ⅲ′））对塌方影响区域进行划分;V为空间区域S内施工器械的平均易损性值;MV为施工器械的市场价值（Market Value）。

对于灾害体处治所需费用，需综合考虑灾害体对既有支护结构的损坏、清除灾害体以及加固处理所需费用，建立R的计算式

R=P×∑（C+C+C）（12）

式中：C为支护结构损坏费用（Cost of Existing Supporting Structure Damage）;C为灾害体清除费用（Cost of Disaster Clean）;C为灾害区修复费用（Cost of Disaster Repair）。

而工期延误经济成本是指事故处治期间所需支付的额外费用，主要包括工人工资、设备租赁费用、现场管理费用，进而建立R的计算式

R=P×∑（（C×n+C×n+C）×

∑（T+T））（13）

式中：C为工人工资（Cost of Worker Salary）;C为机械租赁费用（Cost of Machinery Leasing）;n为租赁器械数量（number of machineries）;C为现场管理费用（Cost of Site Management）。

综合式（10）～式（13），塌方事件导致的经济损失R为

R=P×

∑[（P×P×V×MV）+

（C+C+C）+

（（C×n+C×n+C）×

∑（T+T））]（14）

4 塌方风险接受准则

作为风险管理决策的依据，风险接受准则是各国开展安全风险管理的重要研究内容。为开展塌方风险的定量化评价，建议基于ALARP原则建立相应的风险接受准则。

4.1 ALARP原则

ALARP（As Low As Reasonably Practicable）原则又称最低合理可行原则，其含义是：风险客观存在于工业活动中，不可能被彻底消除，但可通过一定措施降低;但当风险水平较低时，进一步降低风险所需的成本会急速增长，需平衡风险水平和对应的控制成本。

如图4所示，整个区域被容忍线和接受线分为风险不可接受区、ALARP区、风险可接受区。位于容忍线之上（风险不可接受区）的风险，必须采取措施至少降低至ALARP区，在此过程中往往不计成本;位于容忍线和接受线之间（ALARP区）的风险，需通过成本收益分析，结合具体需要，决定是否进一步采取控制措施;位于接受线以下的风险，无需考虑进一步采取风险控制措施。

4.2 人员伤亡风险接受准则

人员伤亡风险接受准则包含个人风险接受准则和社会风险接受准则。个人风险是指长期处于某一特定场所的未采取任何防护措施的人员由于遭受某种危害事故而死亡的概率。社会风险是指某项事故发生后特定人群遭受伤害的概率和受影响人数之间的相互关系。相比而言，个人风险表示的是某一特定地点单个人员的伤亡概率;而社会风险表示的是某一区域的总体伤亡情况，并不局限于具体某个地点。

关于社会风险，采用基于死亡数值的概率密度函数方法，即用年死亡人数的期望值来表示，也就是通常所说的潜在生命损失（Potential Loss of Life），表达式为

E（N）=∫xf（x）dx（15）

式中：N为工程的年死亡人数;x为可能的死亡人数;f（x）为年死亡人数的概率密度函数;E（N）为年死亡人数的期望值。

F-N曲线是一条各种事故所容许发生的限制曲线，其表达式为

1-F（x）=P（N>x）=∫^∞f（x）dx（16）

式中：F（x）为年死亡人数的概率分布函数;P（N>x）为工程年死亡人数N超过x的概率。

因而，关于社会风险接受准则，通常在双对数坐标轴中运用F-N曲线表示死亡人数与超越概率之间的函数关系。即横轴表示死亡人数，纵轴表示风险事故死亡人数超过某一数值的概率。结合定义，应用F-N曲线表示社会风险接受准则的表达式为

1-F（x）<Cx（17）

式中：C为曲线在纵轴上的截距;n为曲线的斜率，取值与风险态度有关：风险中立则n=1，风险厌恶则n=2。

对于个人风险和社会风险，通过结合工程实际，参照现有准则标准（见文献[25]），结合专家调研确定相应的标准值，建立适用于具体工程的人员伤亡风险接受准则。

4.3 经济损失风险接受准则

在经济风险接受准则领域，通常运用F-D曲线表示经济损失与超越概率之间的函数关系。与F-N曲线的定义及确定方法类似，F-D曲线与经济损失的期望值可以由经济损失的概率密度函数得出。

1-F（x）=P（D>x）=∫ f（x）dx（18）

E（D）=∫ xf（x）dx（19）

式中：D为工程的经济损失;x为可能的经济损失;f（x）是经济损失的概率密度函数;F（x）是经济损失的概率分布函数;P（D>x）为工程经济损失D超过x的概率;E（D）是经济损失的期望值。

参照社会风险接受准则，应用F-D曲线表示经济风险接受准则的表达式为

1-F（x）<Cx（20）

关于经济风险接受准则，相比而言，其受国情、工程属性以及个人（业主）承受风险能力的差异影响更为显著。在中国现有的风险管理指南和规范中，基于风险矩阵，建立了定性的接受准则，但在经济损失标准方面存在较大差异，因而需结合具体工程特点以及建设方的承受能力，运用专家调研等方法建立适用的经济风险接受准则。

4.4 工期延误风险接受准则

关于工期延误风险接受准则的制定，借鉴经济风险接受准则的经验，应用F-T（Time Delay）曲线来表示工期延误时间与超越概率之间的函数关系。结合F-N曲线的定义及确定方法，F-T曲线与工期延误时间的期望值由工期延誤时间的概率密度函数得出。

1-F（x）=P（T>x）=∫ f（x） dx （21）

E（T）=∫ xf（x）dx（22）

式中：T为工期延误时间;x为可能的工期延误时间;f（x）是工期延误时间的概率密度函数;F（x）是工期延误时间的概率分布函数，为工期延误时间T超过x的概率;P（T>x）是工期延误时间的期望值。

应用F-T曲线表示工期延误风险接受准则的表达式为

1-F（x）<Cx（23）

5 案例分析

为说明所建立的定量化评估模型的实用性和适用性，选取中国高放废物地下实验室的（试验）主巷道工程为例，开展拟采用钻爆法施工的硐室塌方风险的定量化评估。

主巷道近似水平开挖，埋深为560 m。考虑主应力作用关系和开挖扰动的影响，选取最不利条件下，即垂直于σ条件下开挖的塌方风险分析。

5.1 塌方概率及规模预测

5.1.1 塌方概率计算

关于塌方概率，根据围岩物理力学参数的统计结果和分布类型，应用Monte-Carlo方法生成参数样本，利用FLAC3D和MATLAB数值软件进行硐室开挖塌方的概率分析。

该主巷道断面如图5所示，几何尺寸为8 m×7.667 m。参考弹性力学围岩重分布应力计算理论，认为3倍硐径外的岩体几乎不受开挖影响。故综合主巷道断面尺寸和開挖边界影响，设定数值模型的几何尺寸为58 m×67.667 m×10 m，如图5所示。关于模型的边界条件，两侧为水平约束，顶底部为竖向约束。初始应力条件则是根据文献[30]中新场处的地应力回归分析结果施加节点力。在数值计算过程中，采用全断面开挖方式进行模拟，开挖进尺为3 m。

计算所需的围岩物理力学参数统计结果以及应用Monte-Carlo方法生成的参数随机样本如表3及图6～图8所示。模型计算中选用的本构模型为Hoek-Brown模型，其准则参数如表4所示。

根据数值计算分析统计结果，该主巷道塌方概率为

P=NN=2350 000=4.6×10（24）

5.1.2 塌方体积计算

根据该主巷道的断面尺寸，假定塌落拱上方边界近似为抛物线，则塌方断面面积为

S=2.6×7.667+∫2h6.6xdx+

∫2.6674x+h-hdx≈

4.4h+27.0 m（25）

根据开挖进尺，塌方体体积为

V=13.2h+81.0 m（26）

结合新场处围岩质量等级，参照表1，可得V的均值和方差为

E（V）=103.31

D（V）=13.60（27）

假定V服从正态分布，则V ～N（103.31，13.602），其概率密度函数为

f（x）=12π×13.60×e2×13.60（28）

5.2 塌方风险损失分析

5.2.1 人员伤亡损失

结合塌方概率和表5所示的人员伤亡计算信息，计算得到个人人员（施工人员）死亡概率为4.60×10。根据人员分布数量和相应的分布类型（假定均匀分布）以及对应于不同伤亡程度的人员易损性V，计算得到塌方导致的人员伤亡程度分布如图9所示。

5.2.2 工期延误损失

由式（9）和式（27）可得工期延误时间（T+T）～N（6.20， 0.82），概率密度函数为

f（x）=12π×0.82×e2×0.82（29）

对应的概率分布曲线如图10所示。

5.2.3 经济损失

基于表6～表8的数据，结合式（10）～式（14）、式（27）可得经济损失～N （173.04， 83.15），概率密度函数为

f（x）=12π×83.15×e（30）

对应的概率分布曲线如图11所示。

5.3 塌方风险损失评价

基于已经建立的高放废物处置地下实验室建设期风险接受准则，开展该工程开挖塌方风险损失定量化评价，其结果如图12～图14所示。

可见，依据建立的定量化风险接受准则，该工程塌方导致的人员伤亡风险、工期延误风险、经济损失风险均处于ALARP区，需根据风险水平和控制成本的相对关系制定相应的管控措施。

6 结论

塌方是隧道等地下工程建设中一种常见的灾害，往往会造成严重后果。鉴于当前定性开展风险评估的局限性，针对应用钻爆法施工的山岭隧道，提出一种塌方风险定量化评估模型：

1）应用可靠度理论和普氏平衡拱理论，实现隧道塌方发生概率及其规模的定量化分析。

2）利用ALARP原则和F-N曲线建立可量化的风险接受准则，实现塌方风险的定量化评估。

3）以中国高放废物地下实验室的（试验）主巷道工程为例，开展所建立塌方风险定量化评估模型的实用性和适用性分析，其结果可为今后工程的安全建设提供一定参考。

综上分析，所建立的塌方风险量化评估模型可以为隧道等地下工程塌方风险的定量化分析与评价提供一定的借鉴和指导。但考虑到所应用的工程案例还未施工，在今后的研究中，还需进一步结合工程实际对该塌方风险量化评估模型进行改进和完善。

致谢：

感谢核工业北京地质研究院给予本研究的大力支持和资助，感谢评审专家和编辑部老师给予的宝贵意见和建议。

参考文献：

[1] 吕擎峰， 霍振升， 赵本海， 等. 基于模糊层次和后果当量法的隧道塌方风险评估[J]. 隧道建设（中英文）， 2018， 38（Sup2）： 31-38.

LYU Q F， HUO Z S， ZHAO B H， et al. Risk assessment of tunnel collapse based on fuzzy hierarchy and consequences equivalent method [J]. Tunnel Construction， 2018， 38（Sup2）： 31-38. （in Chinese）

[2] XU Z G， CAI N G， LI X F， et al. Risk assessment of loess tunnel collapse during construction based on an attribute recognition model [J]. Bulletin of Engineering Geology and the Environment， 2021， 80（8）： 6205-6220.

[3] 黃宏伟， 张东明. 长大隧道工程结构安全风险精细化感控研究进展[J]. 中国公路学报， 2020， 33（12）： 46-61.

HUANG H W， ZHANG D M. Recent progresson refined sensing and control of safety and risk of long and large-scale tunnel lining structures [J]. China Journal of Highway and Transport， 2020， 33（12）： 46-61. （in Chinese）

[4] 陈舞， 张国华， 王浩， 等. 基于T-S模糊故障树的钻爆法施工隧道坍塌可能性评价[J]. 岩土力学， 2019， 40（Sup1）： 319-328.

CHEN W， ZHANG G H， WANG H， et al. Evaluation of possibility of tunnel collapse by drilling and blasting method based on T-S fuzzy fault tree [J]. Rock and Soil Mechanics， 2019， 40（Sup1）： 319-328. （in Chinese）

[5] DEGN ESKESEN S， TENGBORG P， KAMPMANN J， et al. Guidelines for tunnelling risk management： International tunnelling association， working group No. 2 [J]. Tunnelling and Underground Space Technology， 2004， 19（3）： 217-237.

[6] OU G Z， JIAO Y Y， ZHANG G H， et al. Collapse risk assessment of deep-buried tunnel during construction and its application [J]. Tunnelling and Underground Space Technology， 2021， 115： 104019.

[7] 陈龙， 黄宏伟. 岩石隧道工程风险浅析[J]. 岩石力学与工程学报， 2005， 24（1）： 110-115.

CHEN L， HUANG H W. Risk analysis of rock tunnel engineering [J]. Chinese Journal of Rock Mechanics and Engineering， 2005， 24（1）： 110-115. （in Chinese）

[8] 王燕， 黄宏伟， 薛亚东. 钻爆法施工隧道塌方风险分析[J]. 沈阳建筑大学学报（自然科学版）， 2009， 25（1）： 23-27.

WANG Y， HUANG H W， XUE Y D. Risk analysis of collapse for tunnels constructed by drill and blast method [J]. Journal of Shenyang Jianzhu University （Natural Science）， 2009， 25（1）： 23-27. （in Chinese）

[9] 李志强， 杨涛. 浅埋黏土层大跨度隧道施工技术与塌方风险分析[J]. 公路交通科技， 2020， 37（2）： 116-122.

LI Z Q， YANG T. Construction technology of large-span tunnel in shallow clay stratum and collapse risk analysis [J]. Journal of Highway and Transportation Research and Development， 2020， 37（2）： 116-122. （in Chinese）

[10] 李燕，靳春玲，贡力，等. 基于熵理论可拓云模型的引水隧洞塌方风险评价[J]. 长江科学院院报， 2021.

LI Y， JIN C L， GONG L， et al. Risk assessment of diversion tunnel collapse based on entropy theory -extension cloud method [J]. Journal of Yangtze River Scientific Research Institute， 2021. （in Chinese）

[11] MA C H， YANG J， CHENG L， et al. Research on slope reliability analysis using multi-kernel relevance vector machine and advanced first-order second-moment method [J/OL]. Engineering with Computers. https：//doi.org/10.1007/s00366-021-01331-9

[12] ALIZADEH M， SADRAMELI S M. Indoor thermal comfort assessment using PCM based storage system integrated with ceiling fan ventilation： Experimental design and response surface approach [J]. Energy and Buildings， 2019， 188/189： 297-313.

[13] FAN C L， LIAO Y D， ZHOU G， et al. Improving cooling load prediction reliability for HVAC system using Monte-Carlo simulation to deal with uncertainties in input variables [J]. Energy and Buildings， 2020， 226： 110372.

[14] GRIFFITHS D V， FENTON G A. Probabilistic slope stability analysis by finite elements [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2004， 130（5）： 507-518.

[15] TSCHUCHNIGG F， SCHWEIGER H F， SLOAN S W. Slope stability analysis by means of finite element limit analysis and finite element strength reduction techniques. PartⅡ： Back analyses of a case history [J]. Computers and Geotechnics， 2015， 70： 178-189.

[16] 盛驟， 谢式千， 潘承毅. 概率论与数理统计[M]. 4版. 北京： 高等教育出版社， 2008.

SHENG Z， XIE S Q， PAN C Y.Probability theory and mathematical statistics [M]. 4th edtion. Beijing： Higher Education Press， 2008. （in Chinese）

[17] 肖明清， 徐晨. 深埋小净距隧道围岩压力代表值探讨[J]. 铁道工程学报， 2020， 37（10）： 83-89.

XIAO M Q， XU C. Discussion on representative value of surrounding rock pressure in deep buried neighborhood tunnel [J]. Journal of Railway Engineering Society， 2020， 37（10）： 83-89. （in Chinese）

[18] 冯卫星，况勇，陈建军. 隧道塌方案例分析[M]. 成都： 西南交通大学出版社， 2001.

FENG W X， KUANG Y， CHEN J J. Case analysis of tunnel collapse [M]. Chengdu： Southwest Jiaotong University Press， 2001. （in Chinese）

[19] MEYER A， NAGPAL R. Permutations and combinations： Mathematics for computer science. Course notes 9 [M]. Massachusetts Institute of Technology： 2002.

[20] 企业职工伤亡事故分类： GB 6441—1986 [S]. 北京： 中国标准出版社， 1986.

The classification for casualty accidents of enterprise staff and workers： GB 6441-1986 [S]. Beijing： Standards Press of China， 1986. （in Chinese）

[21] 事故伤害损失工作日标准： GB/T 15499—1995 [S]. 北京： 中国标准出版社， 1995.

The lost workdays STANDARD for injury accidents： GB/T 15499-1995 [S]. Beijing： Standards Press of China， 1995. （in Chinese）

[22] 李志宏. 基于全寿命期风险分析的路堑与隧道方案决策研究[D]. 上海： 同济大学， 2010.

LI Z H. Decision making between cut-slope and shallow tunnel alternatives based on life cycle risk analysis [D]. Shanghai： Tongji University， 2010. （in Chinese）

[23] LI Z H， HUANG H W， XUE Y D. Cut-slope versus shallow tunnel： Risk-based decision making framework for alternative selection [J]. Engineering Geology， 2014， 176： 11-23.

[24] GONG Y H， NIU Z Y， BAI T Y. Societal risk acceptance criteria for gas distribution pipelines based on incident data from the United States [J]. Journal of Loss Prevention in the Process Industries， 2020， 63： 104002.

[25] 仝跃， 黄宏伟， 张东明， 等. 高放废物处置地下实验室建设期风险接受准则[J]. 中国安全科学学报， 2017， 27（2）： 151-156.

TONG Y， HUANG H W， ZHANG D M， et al. Research on risk acceptance criteria for construction of HLW geological disposal URL [J].China Safety Science Journal， 2017， 27（2）： 151-156. （in Chinese）

[26] FARMER F R. Siting criteria-a new approach [C]//Proceedings of the IAEA symposium on nuclear siting， 1967： 303-29.

[27] JONKMAN S N， VAN GELDER P H A J M，VRIJLING J K. An overview of quantitative risk measures for loss of life and economic damage [J]. Journal of Hazardous Materials， 2003， 99（1）： 1-30.

[28] 劉佑荣， 唐辉明. 岩体力学[M]. 北京： 化学工业出版社， 2009.

LIU Y R， TANG H M. Rock mechanics [M]. Beijing： Chemical Industry Press， 2009. （in Chinese）

[29] 闫军涛， 胡潇， 刘波. 上软下硬复合地层盾构隧洞开挖面稳定性研究[J]. 隧道建设（中英文）， 2020， 40（2）： 223-230.

YAN J T， HU X， LIU B. Stability of shield tunnel excavation face in upper-soft and lower-hard composite strata [J]. Tunnel Construction， 2020， 40（2）： 223-230. （in Chinese）

[30] 仝跃， 陈亮， 黄宏伟. 高放废物地下实验室北山预选区岩爆风险预测[J]. 地下空间与工程学报， 2016， 12（4）： 1055-1063.

TONG Y， CHEN L， HUANG H W. Risk prediction on rockburstin Beishan pre-selected area for underground research laboratory of high-level radioactive waste [J]. Chinese Journal of Underground Space and Engineering， 2016， 12（4）： 1055-1063. （in Chinese）

（编辑 王秀玲）