基于模糊理论的地铁深基坑非对称施工安全风险评估

吴波 赵睿 蒙国往 陈辉浩 黄惟 刘家粱 程懿

摘 要：地鐵深基坑非对称施工比一般深基坑工程施工难度更大、风险性更高。为合理有效地对地铁深基坑非对称施工工况进行风险评估，以广州某地铁深基坑工程为依托，构建了以围护结构、既有线车站非对称土压力、基坑环境、周围环境和现场安全管理为基准的风险评价指标体系。采用模糊层次分析法和多级模糊综合评判法，建立了地铁深基坑非对称施工的评估模型。由定量计算结果得到深基坑非对称施工在评价集中对应的风险等级，与实际工程情况相吻合。根据评估结果得到各指标所占权重大小，可采取相应措施来降低对应风险。

关键词：地铁深基坑;非对称施工;施工安全;风险评估;模糊理论

中图分类号：TU753.1 文献标志码：A 文章编号：2096-6717（2022）05-0008-08

收稿日期：2021-07-05

基金项目：国家自然科学基金（51678164、52168055）;广西自然科学基金（2018GXNSFDA138009）;江西省自然科学基金（20212ACB204001）;广东省高等职业院校珠江学者岗位计划（2019）

作者简介：吴波（1971- ），男，博士，教授，主要从事隧道与地下工程技术研究，E-mail：813792833@qq.com。

Received：2021-07-05

Foundation items：National Natural Science Foundation of China （No. 51678164， 52168055）; Natural Science Foundation of Guangxi （No. 2018GXNSFDA138009）; Natural Science Foundation of Jiangxi Province （No. 20212ACB204001）; Project Supported by GDHVPS （No. 2019）

Author brief：WU Bo （1971- ）， PhD， professor， main research interests： tunnel and underground engineering technology， E-mail： 813792833@qq.com.

Safety risk assessment of asymmetric construction of subway deep foundation pit based on fuzzy theory

WU Bo， ZHAO Rui， MENG Guowang， CHEN Huihao， HUANG Wei， LIU Jialiang， CHENG Yi

（1. College of Civil Engineering and Architecture， Guangxi University， Nanning 530004， P. R. China; 2. School of Civil and Architectural Engineering， East China University of Technology， Nanchang 330013， P. R. China; 3. School of Architectural Engineering， Guangzhou City Construction College， Guangzhou 510925， P. R. China）

Abstract：Compared with the common deep foundation pit engineering， the asymmetric construction of subway deep foundation pit is more difficult and risky. To conduct risk evaluation of the asymmetric construction reasonably and effectively， a risk evaluation index system was established based on enclosure structure， asymmetric soil pressure of existing stations， foundation pit environment， surrounding environment and site safety management， which rely on a subway deep foundation pit project in Guangzhou. Fuzzy analytic hierarchy process and multi-level fuzzy comprehensive evaluation method were used to set up an evaluation model for asymmetric construction of subway deep foundation pit. According to the quantitative calculation results， the risk ranking of asymmetric construction risk of deep foundation pit could be obtained， which match well with the evaluation set and the practical engineering.According to the weight of each index obtained from the evaluation results， relevant measures can be taken to reduce the risk.

Keywords：subway deep foundation pit; asymmetric construction;construction safety; risk assessment; fuzzy theory

截至2020年底，中国共有45个城市开通城市轨道交通运营线路244条，运营线路总长度7 969.7 km。其中，地铁运营线路6 280.8 km，占比78.8%。以上数据显示，中国城市化进程正在稳步推进，城市轨道交通建设也保持着快速增长的态势。由于地铁车站周围通常存在密集的已建或在建建（构）筑物，施工环境复杂多变。在地铁车站深基坑施工期间，不仅需要保障基坑自身施工安全，还应该降低对周边建筑物、道路管线等的影响。所以，针对地铁深基坑安全施工，需要提前进行施工风险评估，制定相应的安全施工方案，降低施工风险。

多年以来，已经有许多学者针对地铁深基坑风险评价进行了研究。Wei等针对已有数据的不完整性和模糊性，提出了一种基于模糊证据推理的深基坑建设项目总体风险水平评估方法;Valipour等在深基坑风险评估中引入SWARA（逐步权重评估比率分析）来处理专家判断的模糊性，同时，使用COPRAS（复杂比例评估）进行风险排序;Meng等将深基坑风险损失细化为5个指标，并赋予5个指标不同的权重，同时，给出专家权重的评价指标，改进了模糊层次评价方法;黄建华等引入贝叶斯网络模糊理论，对基坑围护工程施工风险进行等级划分;程鸿群等采用区间数理论等对层次分析法进行改进，降低了传统量化方法的主观性;张胜昔等通过G-FAHP理论，构建了深基坑施工评估模型，并得到各指标的风险排序;潘海泽等针对传统静态评估方法的不足，引入基于动态变量的突变级数法对地铁深基坑进行了风险评估;王景春等应用熵权法对深基坑评价指标加权，并结合二维云模型确定了地铁车站深基坑风险评估等级;唐建新等将模糊数学理论和实测数据结合使用，建立了多层次指标体系，对地铁深基坑稳定性进行了评价;宋博基于数据包络法和BP神经网络理论，提出了将两者结合的地铁深基坑施工风险评估方法;郎秋岭等采用组合权重与灰色关联度理论相结合的方法，对地铁深基坑开挖稳定性进行了风险评估。

综上所述，已经有很多学者对于地铁深基坑风险评估指标的识别以及风险评估方法的使用进行了尝试，也取得了良好的评估效果。然而，随着各城市轨道交通线路的不断增加，越来越多地出现与既有线车站直接进行接驳的情况，尤其是出现既有线车站不同侧非对称开挖的情况，使得施工环境更加复杂，难以预测。特别是由于既有车站轨行区对位移变形的要求十分严格，而施工力学方面的理论研究仍不成熟，因此，有必要对地铁深基坑非对称施工进行系统的风险评估，以期降低施工风险。

1 地铁深基坑非对称施工评估指标

设最高层为地铁深基坑非对称施工风险S;第2层风险指标集为S=（S，S…S），其中S为第1层第i个子指标集;第3层风险指标集为S=（S，S…S），其中S为第1层第i个子因素集中第j个指标集。

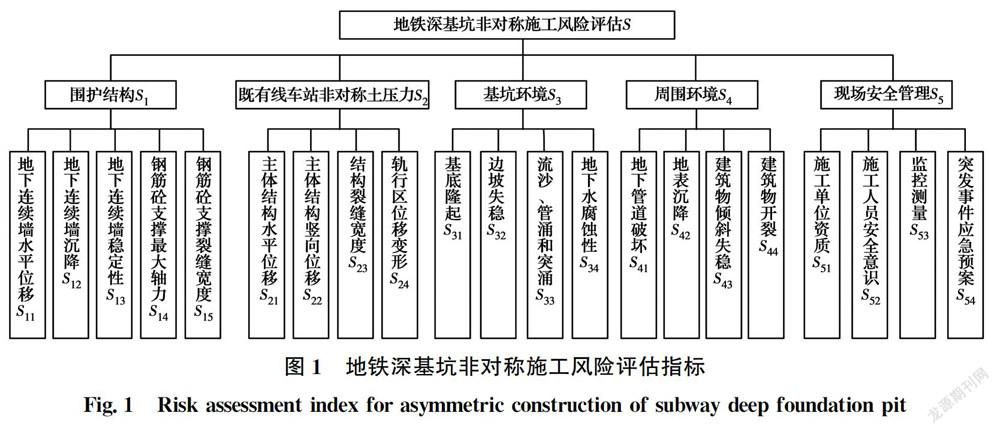
深基坑非对称施工影响因素众多，工程整体仍具有较大的风险性。从地铁深基坑非对称施工安全的角度出发，根据《铁路隧道风险评估与管理暂行规定》、《地铁及地下工程建设风险管理指南（2007）》和《城市轨道交通地下工程建设风险管理规范》（GB50652—2011）以及近年来发生的多起地铁深基坑事故，选取具有代表性的风险因素进行有效的风险识别，并建立系统的地铁深基坑非对称施工风险评价体系，如图1所示。

2 地铁深基坑非对称施工评价方法

层次分析法（AHP）已经被广泛应用于各个领域的评估决策之中，而随着模糊数学的兴起和发展，许多学者将其与AHP理论相结合，逐渐形成了模糊层次分析法（FAHP），该方法处理复杂问题中的模糊信息具有优越性，同时，能够更好地反映出参评专家判断的模糊程度。

多级模糊综合评判法可以利用模糊层次分析法得到的权重值，将多个指标的评价结果按照从下而上的顺序转化为最高层次的单指标结果，有利于对工程整体风险的把控。同时，除最低层次隶属度矩阵由专家给出以外，其余各层隶属度矩阵均由其低一级层次的评估结果形成，在一定程度上考虑了各层次指标之间的关联性。

2.1 模糊层次分析法

其主要步骤如下：

1）建立模糊判断矩阵

选择三角模糊数0.1～0.9标度方法作为判断准则，见表1。通过依次比较同一层次的两个元素，建立基于三角模糊数的模糊判断矩阵R。

式中：r=（r，r，r），其中r为三角模糊数的中值，代表专家根据表1给出的两两元素比较的相对重要程度;r和r為三角模糊数的下界和上界，代表专家判断的模糊程度，差值越大则越模糊。

2）分层计算权重

由图1可知，影响地铁深基坑非对称施工风险评价的指标较多，若不对由参评专家给出的判断信息建立的三角模糊互补判断矩阵进行处理，则不能使其满足一致性的要求。引入参考文献[17]使用的方法，重新调整形成模糊互补判断矩阵V=（v）。

首先，根据式（1）、式（2）计算得到模糊判断矩阵A。

a=1-r-r2（r+r+r）（1）

A=（a）=1a…aaa1a…a…1（2）

然后，根据式（3）～式（5）计算得到调整后的模糊判断矩阵V。

b=r+4r+r6（3）

C=（c）=（ab）（4）

v=12（1+c-c）（5）

验证经过调整后的模糊判断矩阵的一致性，对不满足一致性的矩阵按照式（1）～式（5）重新進行调整，直到模糊判断矩阵完全满足一致性要求后，根据式（6）、式（7）计算各指标权重。

v′=∑ks=1λv（6）

ω=1n-12α+1nα∑nj=1v′（7）

式中：λ为考虑专家能力水平高低的系数，一般认为专家水平相当，取λ=1/k，k为参与打分的专家人数，且有λ之和等于1。ω为最终计算得到的指标权重，选择最重视元素间重要程度的取法，取α=（n-1）/2。

3）验证一致性

假设调整后的模糊判断矩阵V=（v）的可达矩阵为Q=S+·S+·…+·S，则调整后的模糊判断矩阵满足一致性的条件为其对角线元素全部为0，不存在等于1的元素。否则不能通过一致性检验。+·是布尔运算规则，如式（8）所示。同时，通过式（9）的计算可以得到矩阵S=（s）。

0+·0=0 0+·1=1 1+·0=1 1+·1=1（8）

s=1， v≥0.5，i≠j

0， 其他（9）

2.2 多级模糊综合评价

多级模糊综合评价的主要思路是先从处于最底层的指标出发，然后层层推进，逐级评价，直到得到最上端层次的评估结果，其具体步骤如下：

建立评价对象指标集

R={r，r…r}（10）

然后建立评价集

V={v，v…v}（11）

随后建立权重集

W={w，w…w}（12）

紧接着建立单因素隶属度矩阵

X=xx…xxxxx…x…x（13）

最终得到评价对象的评判结果

D=W·X（14）

2.3 建立评价集

参考《公路桥梁和隧道工程施工安全风险评估制度及指南解析》，将地铁深基坑非对称施工安全风险分为4级，具体等级划分如表2所示。

3 案例分析

3.1 工程概况

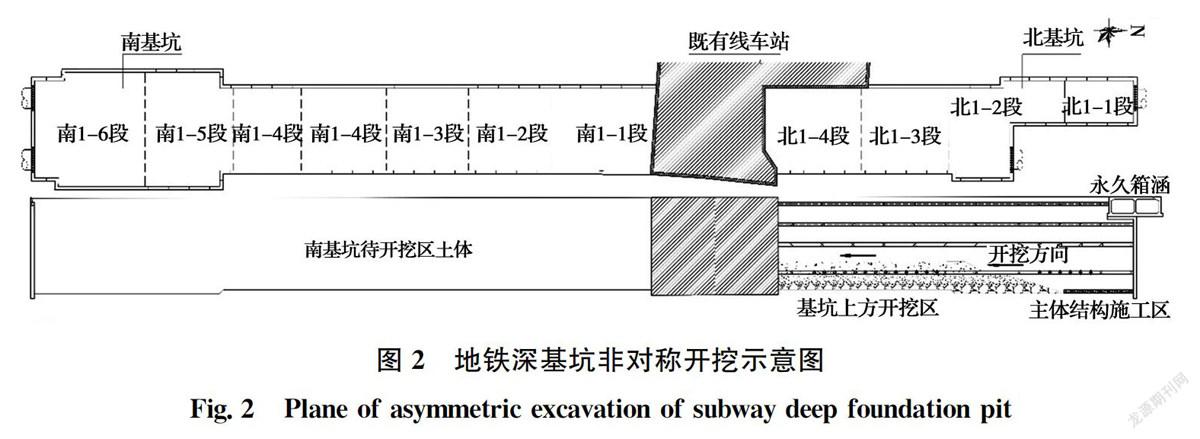
广州地铁某车站为地下3层岛式站台车站，总建筑面积为30 010 m，外包总长322.3 m，标准段宽度为24.1 m。车站西侧及北侧为城中村，东侧为学校和住宅区，南侧为港口码头。建筑密集，管线众多。车站在中间位置与现有运营13号线呈L型换乘，既有线将该项目分隔成南北两个基坑，基坑开挖深度26.98 m，先进行的是北基坑的开挖。北基坑围护结构地连墙共计37幅，墙厚1 m，幅宽6 m，采用四道内支撑，靠近既有车站位置增加了斜撑来弥补减少的非对称土压力。该基坑非对称开挖示意图如图2所示。

该地铁基坑底部大部分位于微风化含砾粗砂岩，局部位于中风化含砾粗砂岩。场地地下水赋存较丰富，有弱腐蚀性，整个场地内地下水位较高，混合水位埋深为2.2～5.0 m。砂层地下水主要靠大气降水和地表水（珠江水系及车站北端头的乌涌）径流补给，地表水与地下水有水力联系，地表水会对地下水补给，基坑发生涌水涌沙的风险较高。

3.2 指标权重确定

进行地铁车站深基坑非对称施工风险评估之前，拟定4位专家按照表1的原则进行打分。其中施工单位专家2名，设计单位专家1名，监理单位专家1名。根据表1的评分标度，将同层次的评价指标两两比较，得到所需要的判断矩阵。以专家A为例，以地铁深基坑非对称施工风险S为判断准则，对第1层次围护结构S、既有线车站非对称土压力S、基坑环境S、周围环境S和现场安全管理S两两元素进行比较，所建立的模糊判断矩阵R为

通过式（1）～式（5）可以得到调整后的模糊判断矩阵V

通过可达矩阵验证模糊判断矩阵V，其满足一致性要求。同理，可以得到其余3名专家评分的模糊判断矩阵V、V、V，分别为

通过式（6）、式（7）可以得到S、S、S、S、S的权重分别为0.286、0.236、0.219、0.156、0.103。同理可得其余各层次评价指标相对于其对应的上一层次指标的权重，详见表3。

3.3 建立单因素隶属度矩阵

经过专家的调查讨论，最终得到隶属度矩阵X，其中x为某评价指标发生事故的可能性概率估计。建立的隶属度矩阵X为

3.4 多级模糊综合评价

3.4.1 一级模糊评价

一级模糊评价是对一类中的最低层次指标进行综合评价。使用式（14）可以计算得到一级模糊评价结果，其中W为最低层次指标权重，X为对应的评价因素隶属度矩阵。具体评价结果为D=（0 0.740 0.260 0），D=（0 0.684 0.316 0），D=（0 0.596 0.404 0），D=（0 0.521 0.479 0），

D=（0 0.552 0.448 0）。

3.4.2 二级模糊评价

二级模糊评价在一级模糊评价的基础上进行，其单因素评价矩阵是由一级模糊评判结果组成，表达式为X=（D D D D D）。通过D=W·X可以得到二级模糊评价结构，其中，W为第二层次指标权重。具体评价结果为

D=（0 0.642 0.358 0）。

3.5 评判结果分析

选用Ⅰ型评判函数，最终结果为P=0.1×0.642+0.01×0.358=0.067 78。由表2可得，本地铁深基坑工程施工风险概率为3级，为可能发生风险。现场实际监测报告显示，既有车站、地连墙以及周围建筑未出现过大的变形和沉降，仅在进行地连墙钢板接缝期间出现了局部的涌水涌沙现象，经过有序抢险之后，未出现设备损失及人员伤亡。该评估结果与现场施工实际情况相符，可以此采取针对性措施来降低风险。

由上述评估结果分析可得，围护结构指标S所占权重最大，其次是既有线车站指标S，可见，地铁深基坑非对称施工的重点是保证围護结构的可靠性以及既有线车站的正常使用功能，应严格按照设计要求以及施工工序要求进行施工。在围护结构指标S中，地下连续墙最大水平位移指标S所占权重最大，设计时应重点考虑地连墙作为永久结构的刚度，同时，施工时要保证围护结构质量，保证加固效果;而既有车站指标S中，轨行区位移变形指标S所占的权重最大，轨行区位移过大，极易导致列车脱轨，造成严重的事故，为控制既有线车站轨行区的变形及沉降能达到地铁保护标准要求，设计时可考虑增加钢筋砼斜撑等措施进行处理。

其余3个指标权重大小排名依次为：S>S>S。在基坑环境指标S中，流沙、管涌和突涌指标S权重最大，而在周围环境指标S中，建筑物倾斜失稳指标S权重最大，这是由于基坑非对称开挖、流沙和管涌现象等容易引起较大的土体变形，当土体变形量超限时，就会引发管线损坏、建筑物开裂，甚至导致建筑物失稳倒塌事故。所以应选择合适的施工工艺，如采用基坑分段开挖、地连墙分段施工的方法进行施工，以减小边坡失稳、基底隆起等风险;同时，做好基坑降水、土体加固，并保障地连墙接缝处刷壁质量，以预防渗流引起的流沙、管涌等现象。

在现场安全管理S中，监控测量指标S所占权重最大，施工现场应重点做好监控测量和预警工作，对该地铁深基坑以及既有线车站结构安全状态实行监测，并按照变化量、变化速率两方面划分预警级别，以此进行现场施工安全管理。

4 结论

相较于一般基坑工程，地铁深基坑非对称施工工况更为复杂，合理正确地识别和评估深基坑非对称施工工程的风险，对整体工程风险管理、保证工程的顺利具有积极意义。基于模糊理论对地铁深基坑非对称施工进行风险评估，得到以下结论：

1）结合实际工程和已有研究，对地铁深基坑非对称施工进行了有效的风险识别，建立了地铁深基坑非对称施工风险评估指标体系。

2）采用模糊层次分析法和多级模糊综合评判理论，可以确定地铁深基坑非对称施工的风险等级。

3）通过评估结果可知，地铁深基坑非对称施工的重点是保证围护结构刚度，减小既有车站轨行区变形位移，同时，应进行实时监控测量，及时预警。

4）使用的模糊层次分析法可以将定性的问题定量化，为地铁深基坑非对称施工风险评估提供一种合理有效的评估方法。

参考文献：

[1] 《城市轨道交通2020年度统计和分析报告》发布[J]. 隧道建设（中英文）， 2021， 41（4）： 691.

Statistical and analysis report of urban rail transit in 2020 [J]. Tunnel Construction， 2021， 41（4）： 691. （in Chinese）

[2] WEI D J， XU D S， ZHANG Y. A fuzzy evidential reasoning-based approach for risk assessment of deep foundation pit [J].Tunnelling and Underground Space Technology， 2020， 97： 103232.

[3] VALIPOUR A， YAHAYA N， MD NOOR N， et al. Hybrid SWARA-COPRAS method for risk assessment in deep foundation excavation project： An Iranian case study [J]. Journal of Civil Engineering and Management， 2017， 23（4）： 524-532.

[4] MENG G W， HUANG J S， WU B， et al. Risk assessment of deep foundation pit construction based on analytic hierarchy process and fuzzy mathematics [J]. Advances in Civil Engineering， 2020， 2020： 1-12.

[5] 黄建华， 杨思， 吴波. 基于贝叶斯网络的基坑围护工程施工风险评估[J]. 武汉大学学报（工学版）， 2016， 49（5）： 733-739.

HUANG J H， YANG S， WU B. Construction risk assessment of foundation pit engineering based on methods of Bayesian network [J]. Engineering Journal of Wuhan University， 2016， 49（5）： 733-739. （in Chinese）

[6] 程鸿群， 佘佳雪， 袁宁， 等. 深基坑工程施工过程风险综合评价[J]. 同济大学学报（自然科学版）， 2016， 44（3）： 491-498.

CHENG H Q， SHE J X， YUAN N， et al. Synthetic evaluation on risk of deep excavation engineering construction process [J]. Journal of Tongji University （Natural Science）， 2016， 44（3）： 491-498. （in Chinese）

[7] 張胜昔， 陈为公， 王会会， 等. 基于G-FAHP的深基坑施工风险评价[J]. 土木工程与管理学报， 2016， 33（5）： 104-109.

ZHANG S X， CHEN W G， WANG H H， et al. Construction risk evaluation of deep foundation pit based on G-FAHP [J]. Journal of Civil Engineering and Management， 2016， 33（5）： 104-109. （in Chinese）

[8] 潘海泽， 贺建， 陈梦捷， 等. 基于突变级数法的地铁车站基坑施工风险研究[J]. 地下空间与工程学报， 2017， 13（3）： 840-845.

PAN H Z， HE J， CHEN M J， et al. Research about construction risk of foundation pit of subway station based on catastrophe progression method [J]. Chinese Journal of Underground Space and Engineering， 2017， 13（3）： 840-845. （in Chinese）

[9] 王景春， 张法. 基于熵权二维云模型的深基坑施工风险评价[J]. 安全与环境学报， 2018， 18（3）： 849-853.

WANG J C， ZHANG F. Risk assessment of the deep foundation pit based on the entropy weight and 2-dimensional cloud model [J]. Journal of Safety and Environment， 2018， 18（3）： 849-853. （in Chinese）

[10] 唐建新， 李欣怡. 基于模糊数学的地铁深基坑稳定性评价[J]. 安全与环境学报， 2018， 18（6）： 2135-2140.

TANG J X， LI X Y. On the stability evaluation of the deep subway foundation pit based on the fuzzy mathematical theory [J]. Journal of Safety and Environment， 2018， 18（6）： 2135-2140. （in Chinese）

[11] 宋博. DEA-BP神经网络下地铁车站深基坑施工安全评价[J]. 中国安全科学学报， 2019， 29（5）： 91-96.

SONG B. Safety evaluation for deep foundation pit construction in metro station based on DEA-BP neural network [J]. China Safety Science Journal， 2019， 29（5）： 91-96. （in Chinese）

[12] 郎秋玲， 王伟， 高成梁. 基于组合权重与灰色关联度分析法的地铁深基坑开挖稳定性评价[J]. 吉林大学学报（地球科学版）， 2020， 50（6）： 1823-1832.

LANG Q L， WANG W， GAO C L. Stability evaluation of deep foundation pit of metro based on grey correlation analysis with combined weights [J]. Journal of Jilin University （Earth Science Edition）， 2020， 50（6）： 1823-1832. （in Chinese）

[13] 中华人民共和国铁道部.铁路隧道风险评估与管理暂行规定（铁建设[2007]200号）[S].北京：中国铁道出版社，2007.

Ministry of Railways of People's Republic of China. Interim provisions on risk assessment and management of railway tunnels [S]. Beijing： China Railway Publishing House，2007.（in Chinese）

[14] 中华人民共和国建设部. 地铁及地下工程建设风险管理指南[S].北京： 中国建筑工业出版社， 2007.

Ministry of Construction of the People's Republic of China. Guide for risk management of subway and underground construction [S]. Beijing： China Architecture & Building Press， 2007.（in Chinese）

[15] 城市轨道交通地下工程建设风险管理规范： GB 50652—2011 [S]. 北京： 中国建筑工业出版社， 2012.

Code for risk management of underground works in urban rail transit： GB 50652-2011 [S]. Beijing： China Architecture & Building Press， 2012. （in Chinese）

[16] 范英， 李辰， 晉民杰， 等. 三角模糊数和层次分析法在风险评价中的应用研究[J]. 中国安全科学学报， 2014， 24（7）： 70-74.

FAN Y， LI C， JIN M J， et al. Research on application of triangular fuzzy number and AHP in risk evaluation [J]. China Safety Science Journal， 2014， 24（7）： 70-74. （in Chinese）

[17] 吴波， 吴昱芳， 黄惟， 等. 基于模糊综合判定法地铁深基坑施工安全风险评估[J]. 数学的实践与认识， 2020， 50（2）： 179-187.

WU B， WU Y F， HUANG W， et al. Safety risk assessment of metro deep foundation pit construction based on fuzzy comprehensive judgment method [J]. Mathematics in Practice and Theory， 2020， 50（2）： 179-187. （in Chinese）

[18] 吕跃进. 基于模糊一致矩阵的模糊层次分析法的排序[J]. 模糊系统与数学， 2002， 16（2）： 79-85.

LV Y J. Weight calculation method of fuzzy analytical hierarchy process [J]. Fuzzy Systems and Mathematics， 2002， 16（2）： 79-85. （in Chinese）

[19] 侯福均， 吴祈宗. 模糊数互补判断矩阵的加性一致性[J]. 北京理工大学学报， 2004， 24（4）： 367-372.

HOU F J， WU Q Z. Additive consistency of complementary judgment matrices with fuzzy numbers [J]. Journal of Beijing Institute of Technology， 2004， 24（4）： 367-372. （in Chinese）

[20] 交通运输部工程质量监督局. 公路桥梁和隧道工程施工安全风险评估制度及指南解析[M]. 北京： 人民交通出版社， 2011.

Engineering Quality Supervision Bureau of Ministry of Transport. Analysis of construction risk assessment system and guide for highway， bridge and tunnel engineering [M]. Beijing： China Communications Press， 2011. （in Chinese）

（编辑 胡玲）