极端负荷下并联有源滤波器谐波补偿方法

杨正东，施浩波

（1.济南供电公司，山东 济南 250001；2.中国电力科学研究院有限公司，北京 100192）

在电网建设不断发展的进程中，电力电子设备已成为越来越多领域不可缺少的应用装置[1]，且部分电力电子设备也已在极端负荷下进行应用，其极端负荷方式包括2种：一是尖峰负荷，即电网部分变电所因主变重载而存在电压偏低问题；二是低谷负荷，即电网部分变电所因下级电网电力电缆线路充电功率过剩而存在无功倒送和电压偏高的问题。但是其在应用中所产生的大量谐波污染势必导致电网中流入过多畸变电流，造成电力装置不能正常运行，引发装置损伤及电力事故[2-4]。因此，谐波补偿方法成为当下众多学者的研究重点。

文献[5]提出了三相四开关并联型有源电力滤波器选择性谐波补偿方法，该方法利用选择性谐波补偿策略对电力滤波器的重点次谐波进行补偿，并采用选择性谐波检测算法对电流值进行计算，以计算结果为基础，采用脉宽调制策略跟踪参考值。以此实现对三相四开关并联型有源电力滤波器的谐波补偿。文献[6]提出了一种有源电力滤波器指定次谐波补偿优化策略，对电流重构波形中各次谐波含量进行调整，并以补偿后电流总谐波畸变率最小原则为基础，建立一个补偿结果评价体系，实现有源滤波器的最优补偿。文献[7]提出一种模块化有源电力滤波器谐波补偿方法，对电力系统次谐波为5，7，11，13为主的有源电力滤波器进行谐波补偿，运用特征次谐波补偿实现对补偿容量的降低。

虽然上述方法能够在不同程度上实现对有源滤波器的谐波补偿，但是在降低电流畸变率方面还有提升空间，但是由于一般情况下，放大器会使用PI控制器进行电流信号追踪，但其需要在所给定的电流为直流量时方可完成对系统的无静差追踪。由于并联有源滤波器控制的给定值为存在数次畸变电流的交流量，因此，对畸变电流信号的无静差追踪不能通过单一的PI控制完成。

针对上述问题，本文设计一种基于PI控制与重复控制理念的复合控制系统。作为极端负荷下并联有源滤波器谐波补偿方法，将电网内由非线性负载谐波产生的畸变电流抵消，解决了单一的PI控制存在的补偿后电流总谐波畸变率较高的问题，从而实现谐波补偿的目的，提升了电流的稳定性。

1 谐波补偿方法

1.1 并联有源滤波器拓扑结构

用于极端负荷下三相四线制系统中的并联有源滤波器的主电路拓扑结构如图1所示。

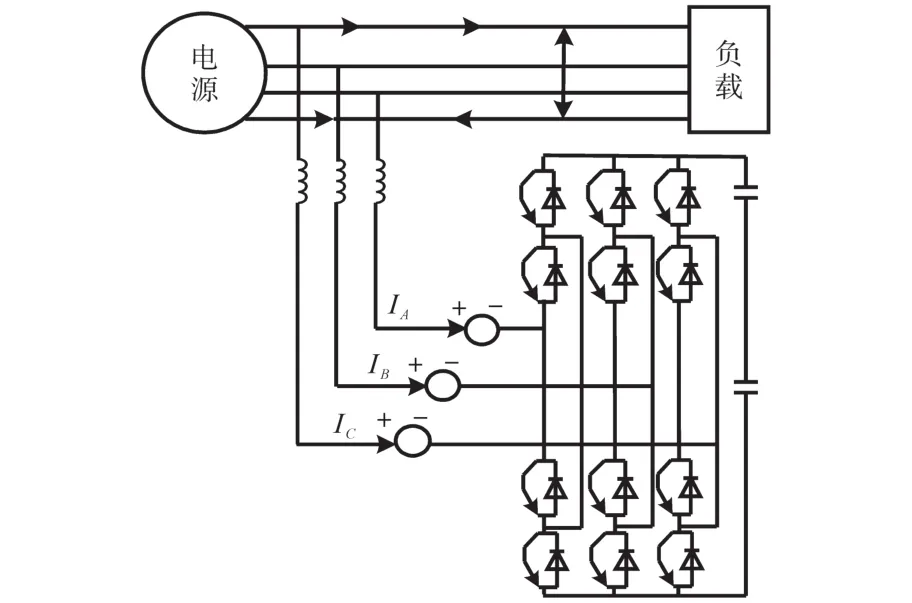
图1 并联有源滤波器拓扑结构电路图Fig.1 Topology circuit diagram of shunt active power filter

由图1可知，通过滞环操控电压源逆变器输出电流，并对给定电流进行追踪，可将并联有源滤波器当成一个能够操控的电流源。图中，IA，IB和IC为检测所得的需要修复的三相畸变电流，以其为例，分析极端负荷下并联有源滤波器谐波补偿方法，实现谐波补偿。

1.2 PI控制与重复控制并联运行的复合控制器

因单一的PI控制对并联有源滤波器电流环的修复能力较为局限，为满足整体三相四线系统的稳定性需求，实现对并联有源滤波器的谐波补偿，提出基于重复控制与PI控制的复合控制系统。由控制理论的内模原理得出的重复控制思想是将整体系统的外部信号数学模型向控制器中导入，外部输入信号的数学模型存在于稳固的闭环系统内，并建立准确性较高的反馈控制系统[8]。

通过检测获得由诸多频率不等的交流量累计而来的畸变电流信号，即为并联有源滤波器的给定信号。通过控制模型中的内模创建各种交流信号，以达到无差追踪畸变电流信号，实现谐波补偿的目的[9]。尽管所检测到的畸变电流信号有许多频率不等的交流量，但是每个基波周期畸变电流信号的波形均为重复出现的状态，因此，这些畸变电流信号的重复周期可选用为基波周期。

1.2.1 并联有源滤波器重复控制器内模与结构

并联有源滤波器重复控制器内模中控制器离散时的采样周期和周期延缓环节二者之间的联系方程为

式中：z(y)为采样周期；f(y)为周期延缓环节；P(y)为重复控制系数；y-M为基波周期；y为相位修复初始值；M为周期输出叠加值。

当叠加当前输入量和上个周期输出量的削弱值时，当前周期的输出即为叠加值。以畸变电流的周期特性为依据，对追踪信号的稳定性与精准性的提升可通过重复控制实现[10]。

依据控制理论中的内模原理得出，当刻画外部输入信号动力学特征的数学模型存在于反馈控制环路中时，反馈控制系统可拥有较好的追踪命令和消除扰动的性能[11]。现实中恒值PI控制即为一种特殊的重复控制，因重复控制器可存在于各种位置，故重复控制系统的控制结构较多，在此以其中一种应用性较高的嵌入式重复控制系统为例，其结构如图2所示。

图2 嵌入式重复控制结构图Fig.2 Embedded repetitive control structure

图2中每个环节的具体情况为：u(y)为重复控制增益，能够令系统保持稳定；Gu为非线性负载；HPR(y)为重复控制器；yg为相位修复，能够在特定频率值中将经过变更的控制对象变成无相位滞后、单位增益环节；T(y)为修复器，为满足重复控制需求，对对象的特点予以变更；ru为重复控制辅助修复器，其为实现系统鲁棒性提升与精准对象模型而设置，令内模变成一个准周期积分环节。

1.2.2 复合控制策略

以基波周期为步长实现重复控制器叠加误差信号，但是其不能将动态响应时间缩短在一个基波周期内。为兼备系统的动态性能与稳定性能，可并联使用动态响应速率高的PI控制策略与重复控制策略，创建新的复合控制系统[12-13]。复合控制结构如图3所示。

图3 复合控制结构图Fig.3 Composite control structure

图3中，HPI(y)为PI控制器，A(y)为针对受控对象的补偿器。采用频域分析及修正控制对象方式，获取PI控制下的稳定运行参数。重复控制器参数在PI控制稳定系统中详细运算过程如下：

1）对1个周期的采样次数进行运算。

2）选择P(y)。当P(y)=1时，重复控制系统能够实现零稳态误差，若想令系统始终处于稳定状态，需令P(y)<1，对系统稳态误差与稳定性综合考虑后，令P(y)取0.97。

3）通过控制对象的幅频特点选取T(y)，通常情况下，可选取二阶低通调节器作为T(y)修复器。当其对60次之内的谐波进行补偿时，可设定终止频率为ea=2 700 Hz，那么此二阶低通调节器可表示为

4）设相位修复系数g的预估值为3，那么相位修复yg即为y3，它能够控制对象在中低频段的相位滞后，并实现对T(y)的修复。

5）重复控制增益u(y)越低，系统的稳定性能越优越，同时，系统的收敛效率降低，稳态误差升高，通过实验选取u(y)的数值为0.6。

1.2.3 固定次数无静差控制技术

对于单频率的畸变电流通过单一的PI控制不能完成对其信号的无静差追踪，针对该问题，建立结合复合控制与固定电流控制器的结构，采用3/2变换得到需要修复的某次畸变电流的直流量，并对其进行复合控制调节[14]。无静差控制系统结构如图4所示。

图4 无静差控制系统结构图Fig.4 Structure diagram of no static error control system

分析图4可知，无静差控制系统在复合控制器的基础上，对增加数个固定次数畸变电流命令修复值的复合控制器进行外环控制。在固定次数畸变电流相应的同步旋转坐标系内，由控制器外环调节控制恒值，能够确保固定次数畸变电流稳态无静差[15]，对并联有源滤波器谐波补偿的稳态性有较大提升。

同时，电流环是无静差控制系统中响应最快的一环，其控制器参数的优劣将直接影响到整个无静差控制系统的性能，为此在系统中加入二次畸变电流修复环，其不仅对复合控制的速率有所保障，而且能够令固定次数的关键畸变电流达到无静差调节的目的。由于使用瞬时值进行调节，因此，当负载改变时，依然能够得到优越的动态性能与稳态性能。

综上，完成极端负荷下并联有源滤波器谐波补偿方法设计。

2 实验结果分析

为检验本文方法的性能，采用搭建极端负荷下包含并联有源滤波器的三相四线制系统实验平台的方式进行实验，在所搭建的实验平台内通过本文方法对谐波进行补偿，通过补偿后的畸变电流波形，验证本文方法的有效性。

实验系统由并联有源滤波器、整流装置与电源系统构成。其中，不控桥负载电阻是18 Ω，控制器为DSP7001-1-0，主电路的参数是110 A，开关器件的耐压水平是1 100 V，电压测量探头为泰克ts1102edu，示波器型号为p2301c，电流测量探头为P7516-Tektronix，畸变电流测量仪器为那普科技PM9811电能质量分析器。实验的关键参数有：开关频率8 kHz，电源相电压与输出电感分别为120 V和3 mH，直流侧电压与直流侧电容分别为120 V和3 200 μF，电网频率为50 Hz。在上述参数设置下，进行实验分析。DSP7001-1-0控制系统的结构图如图5所示。

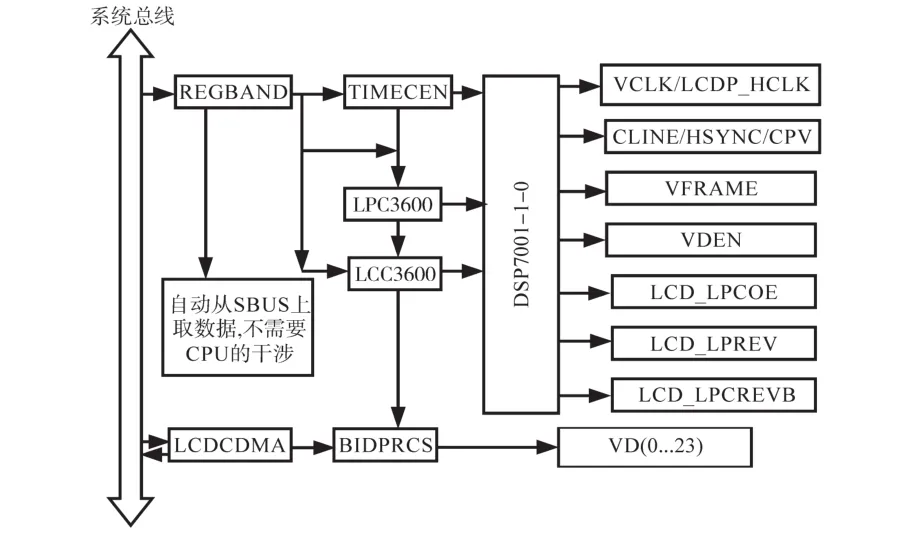
图5 DSP7001-1-0控制系统的结构图Fig.5 DSP7001-1-0 structure diagram of control system

2.1 畸变电流修复

采用本文方法修复实验调节器的畸变电流，以此来实现对谐波的补偿，修复前、后的电流畸变分布情况如表1所示。

表1 修复前、后电流畸变分布状况Tab.1 Current distortion distribution before and after repair%

通过表1能够得出，修复之前实验调节器的畸变电流总谐波畸变率THD为28.6%，通过本文方法修复后的实验调节器畸变电流总谐波畸变率THD下降到6.3%，畸变电流的畸变率改善效果显著。

本文方法修复前、后的实验调节器畸变电流波形如图6所示。

图6 修复前、后畸变电流波形Fig.6 Distorted current waveforms before and after repair

通过图6可看出，采用本文方法对实验调节器畸变电流波形修复后，电流波形的正弦度得到了明显改善，且有效抑制了特定位置的尖脉冲，其原因是本文方法中的复合控制器属于一种以基波周期为步长叠加误差信号的积分控制，能够基于逐周期修复畸变电流波形误差，从而保障了并联有源滤波器谐波补偿的稳态性与精确性。

2.2 实验系统畸变电流修复

一般情况下，在对并联有源滤波器进行谐波补偿时，是在三相平衡的条件下进行的，但是在实际工况下，三相电网电动势幅值与相位均会存在不平衡性，并且并联有源滤波器在A，B，C三相的不均衡安装是导致变电站三相电压不平衡的主要原因，在此条件下，如果不采取有效的措施对谐波进行补偿，将会影响电网的供电质量，因此，对三相不对称畸变电流进行修复具有必要性。

当实验系统处于负载不对称的情况时，采用本文方法对其三相不对称畸变电流进行修复，修复前、后实验系统的三相不对称畸变电流波形如图7所示。

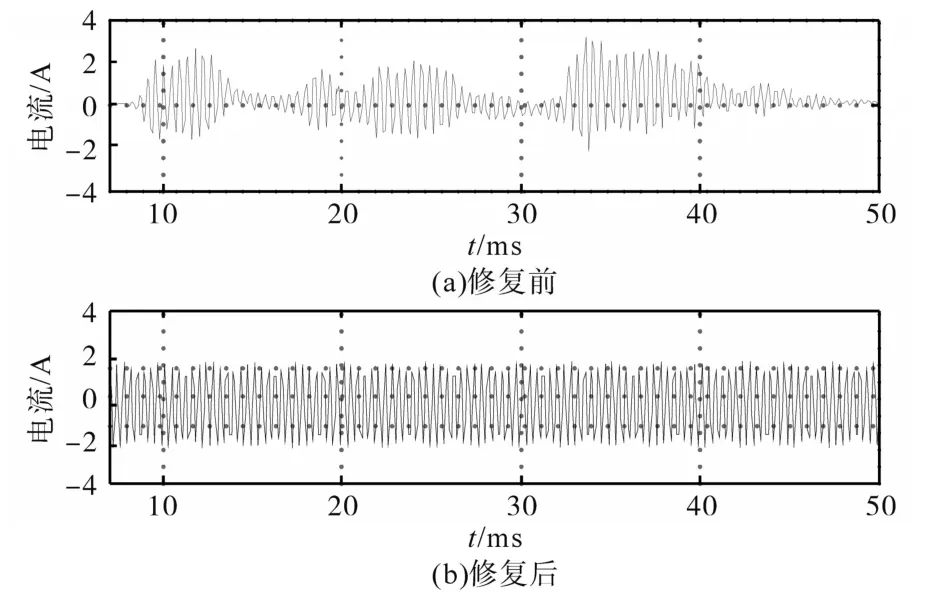
图7 修复前、后实验系统畸变电流波形图Fig.7 Distortion current waveforms of experimental system before and after repair

通过对比图7a～图7b能够明显看出，修复前的畸变电流在10～20 ms，25～35 ms，40～50 ms范围内电流波动幅度较小，在其它时间范围内波动幅度较大，经过本文方法修复后，实验系统的三相不对称负载畸变电流波形动态稳定，波动幅度有规律，畸变电流波形误差明显减少，由此说明，本文方法具备较好的补偿效果。这是因为在固定次数无静差控制技术下，控制系统结构不仅对复合控制的速率有所保障，而且能够令固定次数的关键畸变电流动态稳定，以此达到无静差调节的目的。

为了进一步验证本文方法的有效性，对比加入2次畸变电流修复环前、后波形修复结果，具体如图8所示。

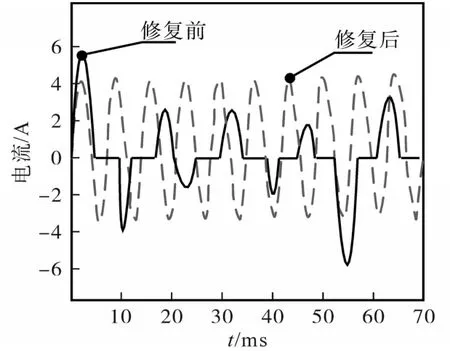
图8 电流修复前、后波形对比图Fig.8 Waveform comparison before and after current repair

分析图8可知，在加入2次畸变电流修复环之前，电流输出呈现出不规律的波形，而加入2次畸变电流修复环之后，电流波形具有一定的规律性，说明加入2次畸变电流修复环后，能够减少传输线的噪声干扰以及分布电阻产生的电压，从而对并联有源滤波器谐波补偿的稳态性起到了提升作用，并且能够实现对畸变电流进行无静差调节的目的。

3 结论

本文针对极端负荷下并联有源滤波器谐波补偿方法展开研究，通过结合PI控制与SAPF重复控制的复合控制系统，实现畸变电流信号的有效追踪，提升畸变电流的稳定性，达到谐波补偿的目的，并通过搭建极端负荷下的三相四线制系统实验平台，检验得出：本文方法补偿后畸变电流的畸变率有效降低，并联有源滤波器与其所在系统的畸变电流波形均更加稳定，补偿效果明显。在未来的研究中，会继续将本文方法用于其它系统中，进一步验证本文方法的有效性。