有限时间内的动车组群分布式协同巡航多智能体控制

魏文军 葛俊德 武晓春

(1.兰州交通大学自动化与电气工程学院,甘肃兰州 730070;2.兰州交通大学光电技术与智能控制教育部重点实验室,甘肃兰州 730070)

1 引言

作为速度为250 km/h以上的旅客专用运输系统,高速列车近年来因其高速便捷和生态友好性而越来越受欢迎.列车自动控制(automatic train control,ATC)系统在列车的安全、可靠和节能运行方面发挥着重要作用[1-3].目前动车组一般采用集中式控制和固定闭塞,更为先进的动车组控制问题的研究已成为热点.本文将利用分布式控制来探讨移动闭塞下动车组群跟踪问题.

在过去的十几年中已进行了大量关于动车组控制算法的研究.文献[4]提出了高速列车的鲁棒自适应控制方法,考虑了运行中的外部扰动,实现列车渐近速度跟踪.文献[5]提出了自适应迭代学习控制的列车跟踪控制算法.以上研究成果是基于单质点模型获得的,假设动车组是刚体,忽略了相邻车厢之间的弹性动力学.针对高速动车组的多动力单元结构,文献[6]采用分布式空间模型描述其动力学模型,设计了各动力单元同步跟踪给定速度的集中式预测控制算法.文献[7]中提出了针对列车位置及速度自适应的控制方法,但在动车组加速或制动时其牵引或制动力会发生急剧的变化,加速列车老化,大大降低了乘客的舒适度.

在过去,ATC一直使用固定闭塞方式,固定闭塞将轨道线路分为固定的区间,每个区间内有一辆列车,其缺点是列车运行跟踪间隔大、线路利用率低等.随着列车自动控制技术,无线通信技术和列车定位技术的发展使得通过提高速度和减少跟踪间隔来进一步提高铁路交通的效率成为可能.文献[8]提出了一种新的信息传输方法,即列车-列车通信技术,该技术可以保证每列车直接与其附近的列车通信,为基于车-车通信的多列车移动闭塞协同控制提供了手段.文献[9]提出了一种移动闭塞条件下的列车追踪运行的协同控制算法.文献[10]提出多拓扑结构下的系统控制模型,通过深入分析多列车耦合的复杂动力学特性,提出单值学习的神经自适应控制律,有效的保证列车之间不发生碰撞的同时尽量缩短列车之间的跟踪距离,提高线路的利用率.但其动车组模型仍然是单质点模型,没有考虑动车组内部的耦合行为.

近年来,基于分布式控制的多智能体技术开始在高速列车协同控制中得到应用[11-14].多智能体系统是分布式人工智能的一个分支,其由多个智能体组成,各个智能体与相邻智能体进行信息交换,互相协调,解决复杂问题[15-17].文献[11]利用势函数来确保列车群在运行过程中相邻列车间的距离保持在一定范围内,但由于势函数为饱和非线性函数,动车组初始条件下速度波动较大,动车组运行的平稳性得不到保障.文献[12]利用多智能体一致性技术,建立了高速动车组多智能体模型,并且设计了相应的分布式控制器,动车组运行更加平稳,但其跟踪时间很长,响应速度慢.

以上文献解决的是动车组协调控制问题,没有考虑动车组达到稳态的时间长短.然而在实际中,动车组在有限时间内收敛并跟踪到给定速度对提升运行效率有很大帮助.为此本文设计了一种新的多智能体有限时间算法,在完成巡航控制的同时加速了收敛时间.该算法假定动车组取消了中心控制节点,动车组的各个动力单元视作智能体.智能体之间通过有限时间一致性协议,在考虑动力单元非刚性连接(即考虑车钩的影响)的情况下,仅仅通过局部通信,不仅可以完成单个动车组的高速巡航控制,同时该算法还能实现满足最小刹车距离的动车组之间的高速巡航控制.智能体之间的分布式控制协议能同时满足单车和多车的控制需求.本文的主要贡献概括如下:

1) 考虑动车组具有动力分散的特性,将每个动力单元视为一个智能体,数学模型考虑了钩缓装置的耦合力,而不是一般模型的刚性连接.动车组之间的头尾智能体通过先进的列车-列车无线通信技术获取相邻动车组的信息,使得动车组群成为多智能体系统.

2) 设计了有限时间分布式协同控制律,该控制律同时实现了两个方面的分布式控制.第一是实现动车组内部在车钩约束下的高速分布式控制,实现动车组内部各个智能体快速追踪到期望速度的同时车钩位移在安全范围内.第二是实现动车组群在保持最小刹车距离的约束下的高速巡航控制,实现了移动闭塞意义上的动车群的追踪运行控制,尽量缩短了列车跟踪时间的同时避免了碰撞.

2 动车组多智能体建模

2.1 单列动车组模型

考虑运行在线路上的一列高速动车组,它由一系列通过车钩连接的动力单元组成,行进中受到滚动阻力和气动阻力的影响.由n个动力单元组成的高速动车组的结构如图1所示.

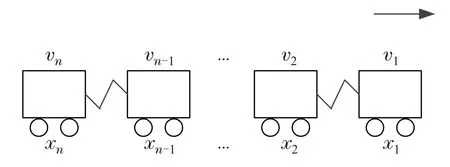
图1 高速动车组结构图Fig.1 Structure of a high-speed EMU

对于具有多个动力单元的高速动车组,相邻的动力单元通过柔性耦合器连接,耦合器位移可以用ei(t)表示,如式(1)所示:

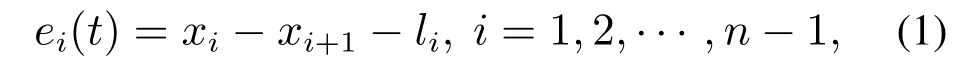
其中:xi,xi+1分别表示第i和第i+1个动力单元所处的位置;li是动力单元的长度.当ei(t)＞0时,耦合器被拉伸并产生内力作为牵引力,有助于各动力单元协同运行.相反,当ei(t)＜0时,耦合器被压缩并产生内力作为制动力使得相邻动力单元保持在可接受的安全间隙中,防止动力单元产生碰撞.

动车组在运行过程中受到3个力的作用,分别是牵引/制动力u、行驶阻力R和耦合力f.耦合器的行为可以通过弹簧模型近似描述,车钩耦合力是动力单元相对位移和相对速度的线性函数,如式(2)所示:

其中ki和di是车钩的刚度系数和阻尼常数.

动车组的行驶阻力由气动阻力和滚动机械阻力构成,动车组的基本阻力由戴维斯公式[18]给出,如式(3)所示:

其中:v是车速;c0,c1,c2是相应的系数,由风洞实验给出;c0+c1v代表滚动机械阻力;c2v2代表气动阻力.可以看出,气动阻力是关于v的非线性函数,随着速度的增大,气动阻力将成为动车组总外部阻力的主要部分,动车组的非线性特性也越来越明显.

假设第i个动力单元的质量、位置和速度分别为mi,xi和vi,动车组运动模型基于分布式驱动型,动车组分成多个动力单元,每个动力单元包括一辆动车和一辆拖车,每个动力单元看作一个智能体.

各动力单元动力学模型如式(4)所示:

为了便于分布式控制律的设计,本文采用代数图论来描述智能体之间的通信拓扑.通信拓扑由加权无向图G=(V,E,A)表示,其中V={v1,v2,···,vn}表示具有n个节点的集合,E ∈V ×V表示该图的边集.边E表示第i个动力单元与第j个动力单元之间可以进行信息交换.如果(vi,vj)∈E则称第j个动力单元是第i个动力单元的邻居,并且动力单元j的邻居可由Nj={vi ∈V(vi,vj)∈E}表示.具有非负元素的A=[aij]是邻接矩阵,并且当(vi,vj)∈E时,权重aij＞0,否则aij=0.

式(5)中,当动力单元i与动力单元j有耦合关系时,=1,否则=0.

2.2 动车组群模型

动车组群系统协同控制如图2所示.在运行过程中,动车组之间的实时信息通过列车-列车无线通信系统完成.由于通信距离有限,动车组只能与其相邻的其他动车组通信,设置β是列车-列车通信的最大距离.动车组内部的通信拓扑选择为列车车厢之间的前后通信物理连接;而动车组之间的通信则选择为后续动车组的首个动力单元和前车的最后一个动力单元进行信息交换,这样选择通信方面的资源占用最小.定义每两个连续动车组之间的跟踪间隔、期望最小跟踪间隔和紧急制动触发距离分别表示为si(t),ls和le.如果跟踪间隔si(t)＜le,则列车将会紧急制动以避免碰撞.

图2 动车组群系统图Fig.2 EMU group system

对于N列高速动车组组成的动车组群系统,其中每列动车组包含ni个动力单元,其信息传输拓扑可用无向图G=(V,E,A)表示.V代表动车组i的节点,每个节点代表智能体,第i列动车组的第j个动力单元的邻域表示为

假设第i列动车组的第j个动力单元的质量,速度和控制输入分别为mi,j,vi,j和ui,j.此时动车组群动力学模型如式(6)所示:

3 有限时间分布式控制律设计

3.1 控制目标

高速动车组群在运行中,首辆动车组的速度以线路允许速度为目标(可从地面应答器获得),并假设动车组群运行在相同速度区间.首辆动车组的期望速度和位置如式(7)所示,其在多智能体系统中被当做虚拟领导者.

对于第i列动车组的第j个动力单元,分别定义其与期望速度和位置之间的速度差和距离差如式(8)所示

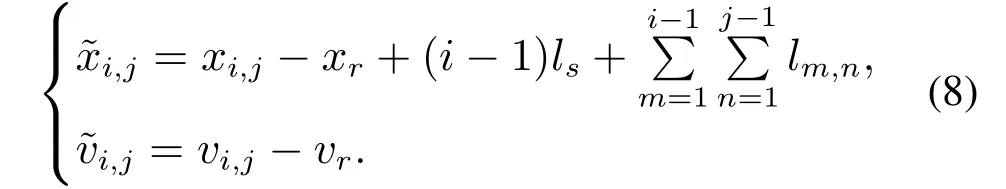
车钩位移ei,j和动车组跟踪间隔si(t)定义如式(9)所示:

动车组分布式控制的目的是为每个动力单元设计有限时间控制律i,j(t)使得:

1) 所有动车组的所有动力单元在有限时间T内跟踪速度-距离曲线,即达到位置和速度一致

2) 任意两连续的动力单元在运行过程中车钩始终在最大最小安全距离内,且每两列连续动车组之间的跟踪间隔si(t)不小于紧急制动触发距离,即

其中h1,h2分别表示车钩可以拉伸的最大距离和压缩的最大距离.

3) 经过有限时间T内车钩位移收敛为0,车钩受力为零,且动车组跟踪间隔最终收敛到ls即

3.2 控制律设计

为了保证动车组群的协同运行,本文设计了有限时间分布式控制律如式(13)所示:

其中:f(x)是齐次项,是非齐次项.如果对于任意的ε ＞0,均有

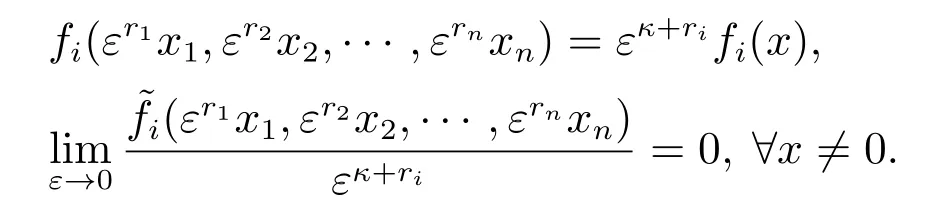
那么系统和带有扩张r=(r1,r2,···,rn)的度κ是齐次的.若函数f(x)连续,x=0是系统的一个渐近稳定平衡点,齐次度κ ＜0,则系统是有限时间稳定的.

定理1考虑在线路上运行的N列动车组组成的动车组群,其中第i个动车组由ni个智能体组成,其动力学模型由式(6)给出.假设初始时刻车钩位移在安全范围内,即−h2＜ei,j(0)＜h1,并且每两列相邻动车组之间的跟踪间隔都大于紧急制动触发距离,即si(0)＞le.提出的有限时间分布式控制法则式(13)可以确保各个动车组在整个运行过程期间满足控制目标式(10)-(12).

证首先证明系统渐近稳定性,在控制律式(13)的条件下,系统(6)可转换为式(14)所示:

选取以下的李雅普诺夫函数V(t)=V1(t)+V2(t)+V3(t)+V4(t)+V5(t),其中:

求取每个李雅普诺夫函数Vi(t)的导数,并应用引理1:

接下来证明有限时间稳定性,定义

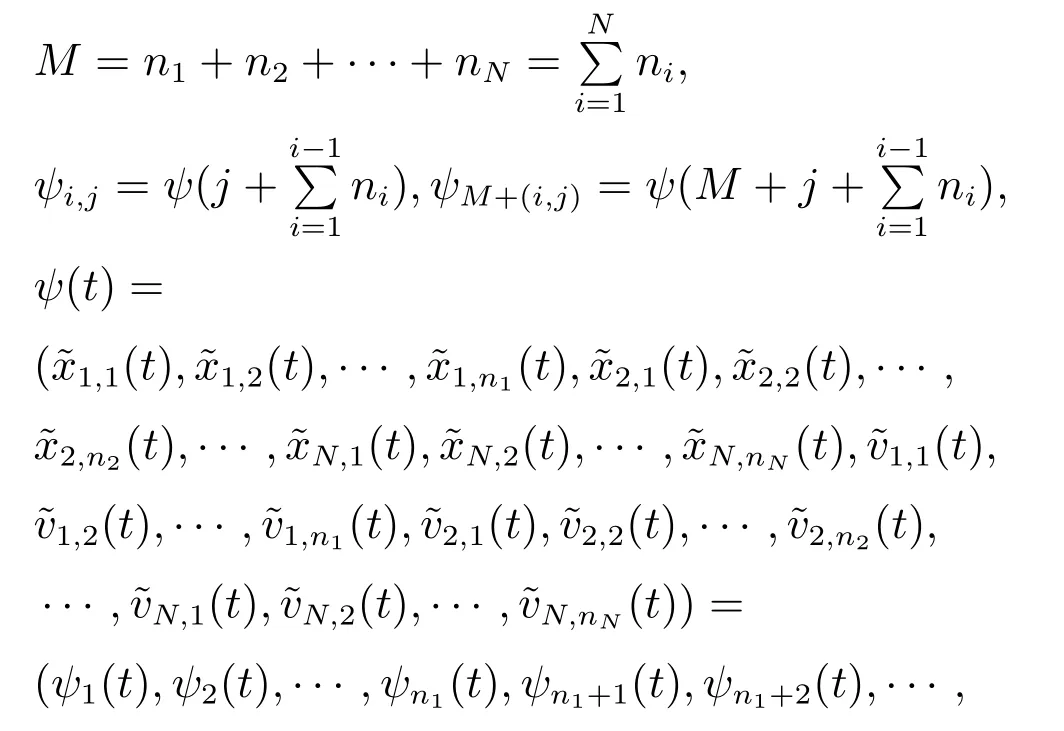
根据引理2可知系统有限时间稳定,即提出的控制法则可以实现控制目标.

4 仿真与分析

为验证本文方法的有效性,假设有3列动车组组成的动车组群系统,每一列动车组具有4个动力单元,其主要参数特性见表1.

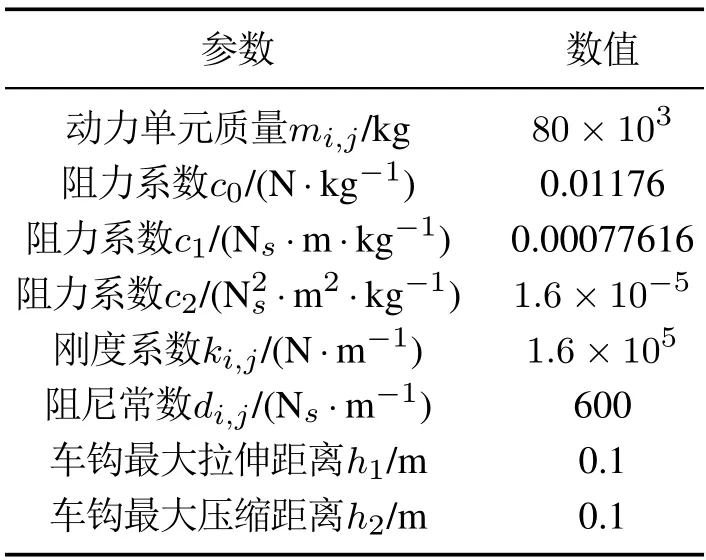
表1 动车组的主要参数[12]Table 1 Main parameters of EMU[12]

同时为了验证不同速度下系统的控制性能,假设首列动车组在以下不同行驶位置有不同的速度,如式(17)所示:

设置动车组的初始位置和初始速度分别为

动力单元的长度li,j=80 m,最小跟踪间隔ls=3000 m,紧急制动触发距离le=1500 m,列车-列车最大通信距离β=10000.控制器参数选择为p1=20,p2=10−4,p3=10,p4=1,µ1=0.05,µ2=0.1,δ1=0.05,δ2=0.03,γ1=1000,γ2=600,α1=0.9.

根据分布式控制规律式(13),仿真结果如图3-6所示.图3表示动车组的速度曲线,图4表示动车组的位置-速度曲线,图5表示车钩位移曲线,图6表示动车组的跟踪间隔.图7表示普通一致性协议下的动车组的速度曲线[12].

图3 高速动车组速度曲线Fig.3 Speed curve of high-speed EMU

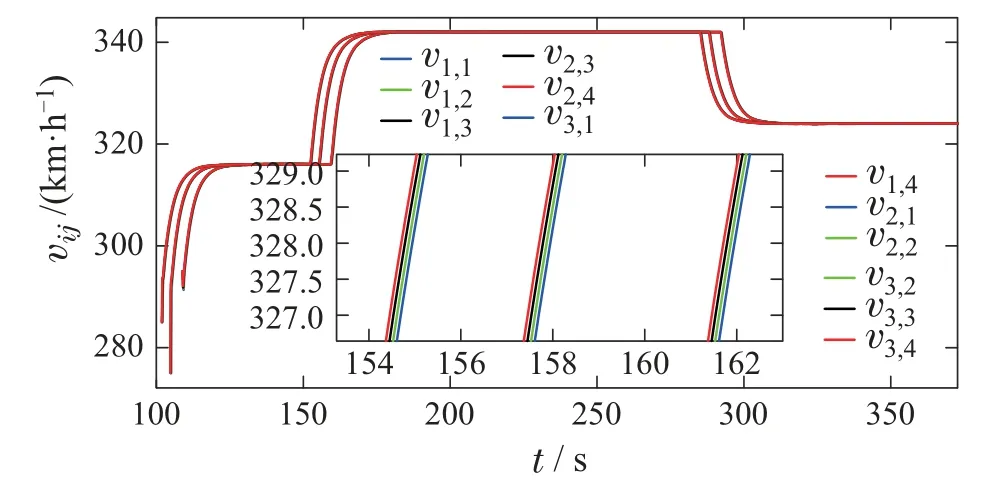
图4 高速动车组速度-位置曲线Fig.4 Speed-position curve of high-speed EMU

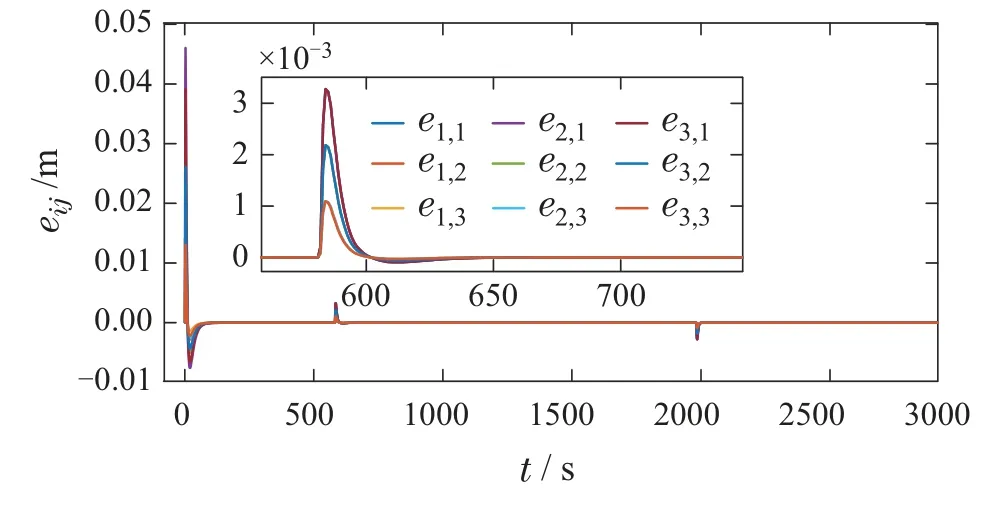
图5 高速动车组车钩位移曲线Fig.5 Displacement curve of coupler of high-speed EMU

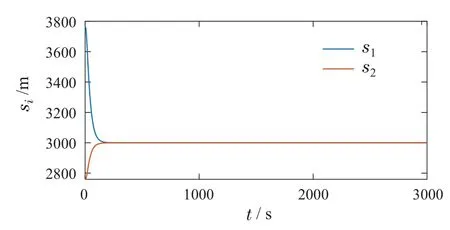
图6 动车组跟踪间隔Fig.6 Tracking intervals between consecutive trains

从图3中和图4中可以看到,从初始时刻开始,在t=200 s左右时,所有动车组快速平滑地跟踪到期望速度vr=316 km/h并保持稳定在此速度,动车组群处于协同状态.对比图7中普通一致性控制算法的速度曲线中收敛时间t=340 s,有限时间控制算法相对于普通一致性算法有以下优点:1)动车组跟踪时间即系统收敛速度大大加快;2)动车组速度变化更为平滑,且无超调,有利于安全行车.

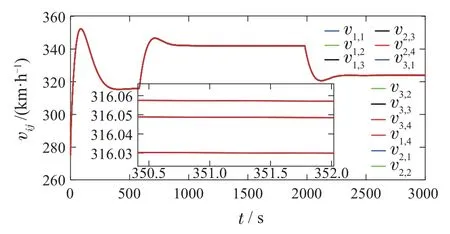
图7 普通一致性算法下的速度曲线Fig.7 Speed curve under common consistency algorithm

在图5中,由于动车组速度增加,车钩从原来的平衡状态开始有小幅的变化,并且在t=200 s时车钩位移收敛到0,重新达到平衡状态.在运行期间所有车钩位移始终在预先设置好的(−0.1 m,0.1 m)之间变化,未超出安全范围.

图6中,连续动车组之间的跟踪间隔在t=200 s时收敛到最小跟踪间隔.从动车组群系统协同控制的仿真结果可以得出,所提出的有限时间分布式控制律可以确保动车组群准确跟踪其所需的速度-距离曲线,达到协同控制目标.

5 结论

本文中研究了动车组群系统的分布式协同控制问题.每列动车组都被建模为一组有序多智能体,每列动车组都可以与其无线通信范围内的动车组交换信息,使得动车组群系统成为多智能体系统.基于本文构建的动车组群多智能体模型,设计了相应的有限时间分布式协同控制律,实现了1)所有动车组速度快速一致;2)每列动车组快速准确跟踪期望的位置-速度曲线;3)车钩位移始终在安全范围内;4)动车组跟踪间隔大于紧急制动触发距离并最终收敛到最小跟踪间隔.最后进行了数值模拟,结果证明了所提出的控制律的可行性和有效性.