采用核鲁棒非负矩阵分解的执行器动态过程故障检测
2022-06-21王印松孙天舒丁梦婷袁环环解沛然
王印松 ,孙天舒 ,丁梦婷 ,袁环环 ,解沛然
(1.华北电力大学自动化系,河北保定 071003;2.华北电力大学控制与计算机工程学院,北京 102206)
1 引言
随着工业过程的日益大型化和复杂,提高控制系统的可靠性尤为重要[1].流程工业中,执行器作为控制系统中的关键部件,工作环境恶劣、故障发生频繁,其故障的发生往往危及整个系统的控制策略,造成巨大的经济损失,因此有关执行器故障检测技术的研究对于提高系统可靠性、安全性,保证正常的生产活动具有极为重要的现实意义[2-3].
当前执行器故障检测的方法可分为基于解析模型的方法、基于经验知识的方法以及基于数据驱动的方法[4-7].基于解析模型的方法主要包括状态估计法[8]、参数估计法[9]、等价空间法[10]这3种方法.其基本思想是利用系统的物理模型对产生的残差进行评价来判断故障是否发生,是一种比较成熟的方法,但是需要精确的模型,而现代系统结构复杂、噪声多、内部变量耦合度高,这都为建立精确模型带来了困难.基于经验知识的方法可分为3大类:专家系统[11]、定性仿真[12]以及模糊逻辑推理[13]的方法.该类方法对模型精度要求不高,但依赖相关技术人员的从业经验对故障进行推理判断,学习性不强且经验知识难以获得.随着计算机技术的发展,基于数据驱动的故障诊断方法受到了人们的关注,它通过提取过程数据来诊断系统故障,不过分依赖经验知识,不受限于复杂的机理过程,包括机器学习法[14]、信息融合法[15]、信号处理法[16]、粗糙集法[17]和统计分析方法[18]等.文献[19]利用扩展卡尔曼滤波观测器估计状态向量,计算不同故障执行器引起的残差序列,利用这些残差所对应的概率对无人机执行器进行故障检测和诊断;对于电液执行器的故障,文献[20-21]提出了支持向量机、深度卷积神经网络等方法来进行检测,面对复杂的数据展现出更好的诊断能力.但是,以上研究通常设定系统工作在稳定工况下,忽略了系统长期处于动态调节过程的实际情况,从而导致在实际检测中效果不佳,及时性不好.针对这样的问题,许多学者使用了其他数据驱动方法对动态过程进行故障检测:文献[22]提出动态主元分析方法,用主成分分析(principal component analysis,PCA)方法进行过程监测,但其不能给出动态元素间的相互关系;文献[23]使用动态内部主元分析(dynamic internal principal component analysis,DiPCA)并结合隐马尔科夫模型(hidden Markov model,HMM)进行动态性分析,实现了动态过程的故障检测.上述研究主要针对稳定过程出现故障的情况,然而执行器具备更加复杂的动态运行过程,这些没有得到关注.
流程工业过程中,由于外界干扰、系统调节、对象模型漂移等因素,执行器更多的处于动态调节中,而不是稳定的状态.此外,故障的发生往往是随机的,动态情况下的执行器故障无法避免,单一的稳态检测极有可能导致检测时延.因此,仅针对稳定工况下的执行器进行故障检测是片面的,考虑执行器动态过程的故障检测,对提高生产过程安全性、可靠性具有重要意义.动态调节过程中,执行器频繁动作,难以获取完备标准的训练集.同时,运行数据的局部线性关系被打破,实现动态过程的故障检测需要及时有效地处理数据中的动态特征和非线性特性,过程干扰等因素也对检测算法的鲁棒性提出了一定的要求[24-25].
非负矩阵分解算法(nonnegative matrix factorization,NMF)是一种非常有效的降维方法[26],但不能很好处理非线性数据集;通过核技巧,可将低维空间数据映射到高维空间,以此实现线性可分,由此提出了基于核函数的非负矩阵分解算法(robust nonnegative matrix factorization,KNMF)[27],KNMF 不仅计算方便、复杂度低,在特征空间内具备NMF所有的数学特性,而且比NMF更加灵活,可以为不同的数据集选用不同的核函数,从而拥有更好的检测性能[28].但一般的KNMF算法并不能适应于所有的复杂工业过程模型.
针对以上问题,本文提出了一种基于KRNMF的执行器故障检测算法.首先,针对动态调节过程缺乏标准训练集的问题,利用基于自动搜索的分段线性化方法从历史数据中建立执行器的动态特性模型,并以此获得用于训练的数据集;其次,针对动态过程的非线性故障检测问题,设计了一种新的算法-核鲁棒非负矩阵分解(kernel robust nonnegative matrix factorization,KRNMF),该算法在KNMF的基础上引入一个稀疏的误差矩阵从而隔离异常状况,提取执行器的有效特征,基于SPE统计量实现动态工况下执行器故障的检测.
2 基于自动搜索的分段线性建模
针对动态过程,利用正常状态下的执行器动态变化历史数据,构建它的流量特性曲线.在此使用基于自动搜索的分段线性化建模方法.采集尽可能包含全行程的执行器动态运行数据,按照控制指令从小到大重排数据样本,并以最小控制指令为起始向后搜索特征区间.在每个特征区间上用最小二乘算法辨识模型.
如下式,其中:f代表流量信号,u是执行器的控制指令,[Ui,Ui+1]表示第i段特征区间.
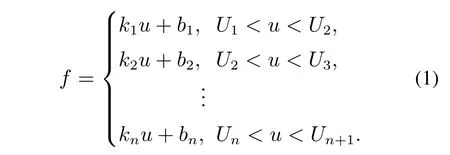
假设样本数目为N,定义如下模型性能指标:

3 核鲁棒非负矩阵分解
3.1 算法描述
KRNMF首先基于KNMF算法,利用核技巧将非线性输入空间的数据映射到线性空间,在特征空间进行矩阵分解时,引入一个误差矩阵通过迭代用以隔离异常信息,从而在实现非线性处理的基础上提高鲁棒性.给定输入数据X ∈Rn×m,n代表变量,m代表样本.通过映射函数Φ(·)将数据映射到高维特征空间F,得到数据矩阵Φ(X)=[Φ(x1)Φ(x2)··· Φ(xm)].在高维特征空间对Φ(X)进行分解

其中:Wφ和Hφ分别是特征空间中映射数据的基矩阵和表示矩阵,Sφ则代表误差矩阵.值得注意的是,Φ(X)是未知的,导致分解过程无法实现,为此在等式两边左乘(Φ(X))T

根据文献[27],核函数可以定义为

令Y=(Φ(X))TWφ,Q=(Φ(X))TSφ,结合式(5)-(6)可以转化为如下形式:
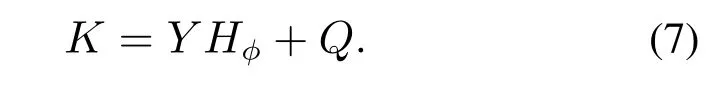
由此,高维特征空间的分解问题转化为了对核矩阵的鲁棒非负分解过程.因此,为求解各矩阵的近似解,定义目标代价函数如下:
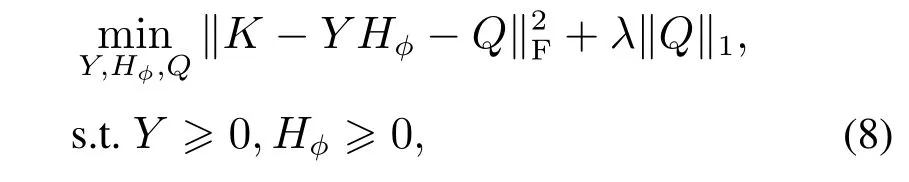
其中:Y和Hφ分别可以看作核矩阵的基矩阵和表示矩阵,Q则代表误差矩阵.
3.2 算法求解
式(8)在同时考虑Y,Hφ和Q时是非凸的,而分开考虑时属于凸优化问题,因此通过局部优化方法求解各部分的近似解.
1) 固定Q,分别优化Y和Hφ,此时式(8)转化为局部优化,令J1代表局部目标函数

然而,Y和Hφ的迭代过程中,使代价函数最小的优化结果并不是唯一的,因此,需要对Y和Hφ添加标准化步骤


2) 固定Y和Hφ,优化Q,此时的优化目标函数形式如下:

应用文献[24]中的定理,考虑一个l1最小化问题
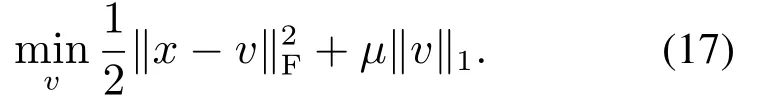
式(17)的特解可以通过定义的软阈值算子Tµ(x)得出

根据上述定理,结合式(16)-(17)的结构特征,得到Q的更新法则

3.3 算法步骤
核鲁棒非负矩阵分解的核心思想是利用核技巧将非线性数据映射到高维线性空间中,从而解决非线性问题.通过将核矩阵分解出稀疏的误差矩阵,隔离异常信息,以此解决鲁棒性问题.根据第3.2节的理论推导,得到KRNMF的算法步骤如表1所示.

表1 KRNMF算法流程Table 1 KRNMF algorithm flow
4 基于KRNMF的故障检测方法
4.1 监控统计量-SPE统计量
本文模仿KNMF算法的平方预测误差(SPE)监控统计量,设计了新的SPE统计量.二者的区别在于,前者仅表示测试量与检测模型的偏离程度,后者表示剔除训练集异常特征后的测试量与检测模型的偏离程度.训练集虽然是正常数据,但并非标准数据,依旧包含部分噪声干扰等异常信息.新的SPE统计量通过引入包含该信息的误差矩阵从而在检测过程中剔除了它的干扰,避免发生误报、漏报.计算公式如下:

评价故障检测性能的指标主要有故障检测率(FDR)[29]、故障延迟时间(FDT)、误报率(FAR)和漏报率(MAR)[30]等.计算公式如下:

如式(23)-(26)所示,故障检测率是指故障样本中,被正确检测的故障情况(TP)占实际故障样本数(TP+FN)的比例;故障延迟时间是指检测到故障的时间(DT)与实际故障发生的时间(AT)的差距;误报率是指正常样本中,判断为故障的情况(FP)占正常样本总数(FP+TN)的比例;漏报率是指故障样本中,判断为正常的情况(FN)占故障样本总数(TP+FN)的比例.因此,故障检测率越高、故障延迟时间越短、误报率越低、漏报率越低,则说明故障检测性能越好.
判断故障的发生通过使用控制限来衡量,本文采取核密度估计法计算控制限.当统计量指标超过控制限时,判断为发生故障;反之,则为正常状态.
4.2 故障检测步骤
基于KRNMF的故障检测具体步骤如下:
步骤1采集正常工况下执行器的历史数据,构建动态特性模型;
步骤2获取实时数据,输入模型得到标准训练集,进行标准化处理,选取合适的核函数,计算核矩阵,并进行中心化和方差归一化;
步骤3参照表1中的步骤3至步骤9的迭代过程,计算基矩阵和残差矩阵;
步骤4根据式(20)-(22),计算监测统计量,使用核密度估计法计算控制限;
步骤5将实时数据基于正常数据的均值和方差进行标准化处理,依据步骤2的方法计算核矩阵;
步骤6根据式(20)-(22),计算新数据集的监测统计量,判断其是否超过正常工况下建模时得到的控制限,如果超出则表明发生故障,反之则为正常.
5 实验验证
本节选取3个案例分别验证KRNMF算法对执行器动态调节过程故障检测的有效性和及时性.包括基于工业控制系统中执行器诊断方法的发展与应用(DAMADICS)平台、基于水箱平台的仿真实验和基于火电厂减温水调节阀的实际数据实验.KNMF,核主成分分析(KPCA)被选作对比算法.3个实验中均采用高斯核函数,核密度估计的置信度设为95%.
5.1 DAMADICS平台
本文以DAMADICS平台[31]为基础,进行执行器故障诊断算法的研究.该平台由欧洲训练基金会在2002年至2006年期间研究开发,充分仿真气动调节阀的工作状态.其气动调节阀由气动执行机构、调节结构、阀门定位器和一些附件组成,平台模拟了气动调节阀可能发生的仿真故障以及几类发生在制糖工艺中的实际故障.因此,在模拟、诊断阀门的故障研究中多有应用.例如,文献[32]利用DAMADICS平台的19种不同故障模式来验证提出的故障检测与诊断方法的有效性.
本文中,首先在DAMADICS平台上,采用正弦信号作为控制指令产生执行器全行程的数据样本,然后,利用基于自动搜索的分段线性化方法建立流量特性曲线.设定模型指标阈值为0.002,初始特征区间长度为样本总数.图1是上下行程的特性曲线(实线)及建模结果(虚线).从图中可以看出,采用本文的建模方法可以有效的搜索到合适的特征区间,并且每个区间内的流量特性的估计能够确保在允许精度范围内.
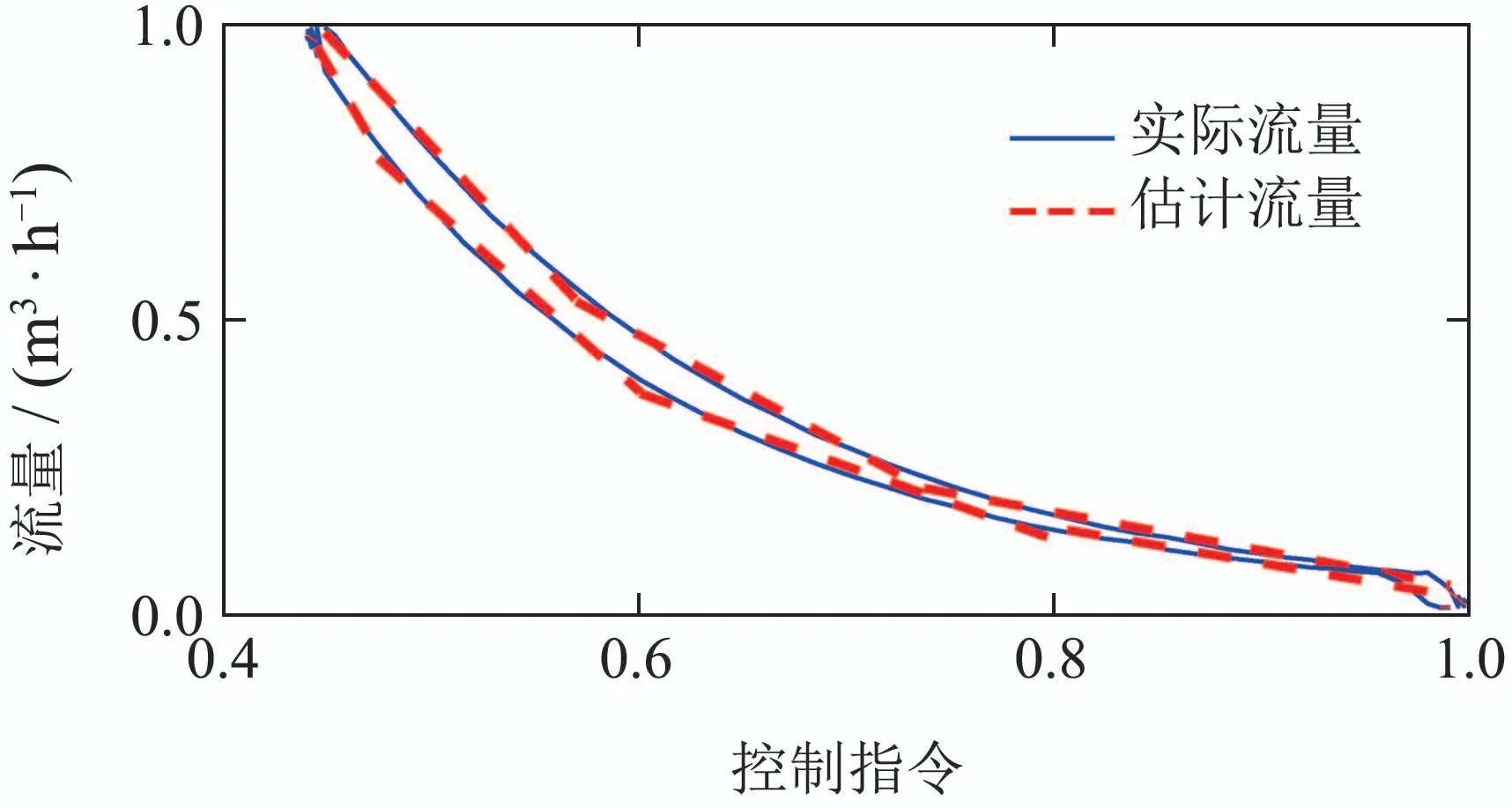
图1 DAMADICS平台执行器流量特性曲线Fig.1 Flow characteristic curve on DAMADICS platform
为了验证本文提出的算法在执行器动态过程中的检测效果,给定正弦信号u=0.28 sin(0.02πt)+0.72作为输入的控制指令,在故障1,6,13,19状态下仿真过程数据,故障在第300 s发生.以检测样本的控制指令为输入,线性化后的特性曲线为模型,可以获得对应控制指令的训练集.
本文算法与KNMF,KPCA方法的检测结果如图2所示.由图2可知,本文算法及构建的SPE统计量能够快速准确的检测出故障的发生:在1~300 s之间,监测统计量保持稳定;在第300 s时,统计量出现突变,超出控制限预示发生故障;301~400 s之间,大部分时间都超过了控制限.对于KNMF算法,故障1的检测在1~300 s出现明显的误判.故障19的检测在300~350 s出现了明显的漏报.对于KPCA算法,在正常状态和故障状态下,其监测统计量都出现了频繁的波动情况,由此还产生了许多误报、漏报的现象.根据上述分析,可以得出以下结论:1)处于正常状态的监测统计量的波动说明KNMF和KPCA不能克服数据的动态特性;2)KNMF和KPCA算法出现误报、漏报的情况反证本文算法引入的误差矩阵实现异常信息的隔离,从而提高故障检测率.


图2 DAMADICS平台仿真实验中各算法的故障检测效果Fig.2 Fault detection effect of each algorithm in the simulation experiment of DAMADICS platform
为了直观对比3种方法的优劣,统计了故障检测率、故障误报率以及故障延迟3个性能指标,如表2所示.从故障检测率来看,面对同样的故障,本文算法的故障检测率最高,KNMF次之,KPCA最差.本文算法中没有误报的情况,个别故障下KNMF存在误报,而KPCA则一直有误报警发生.从故障延迟的角度分析,KRNMF算法的检测延迟最小,即故障检测最及时.因此,3个性能指标都验证本文算法故障检测的准确性和快速性.此外,3种方法均基于同样的训练和测试数据,但是出现了不同的检测结果.KPCA容易出现漏报、误报和故障延迟的原因在于:该方法未能消除样本数据动态变化的特征,反而受其影响.KNMF相比于KPCA,受动态变化的影响较小,因此有较好的故障检测率和误报率,但是KNMF算法在检测故障1和故障19时的延迟较高.这表明,执行器的动态特征数据掩盖了故障的发生,使得KNMF没有及时辨别出故障信号.与这两种方法相比,本文算法既能克服执行器的动态变化的影响,又能挖掘出动态数据中存在的故障特征.

表2 DAMADICS平台仿真实验中各算法性能指标Table 2 Performance indexes of each algorithm in the simulation experiment of DAMADICS platform
5.2 水箱平台
本节基于水箱实验平台设计了一个实现液位控制的单回路系统,实验装置如图3所示.水箱的液位通过传感器和I/O设备输入上位机,PID控制器计算出指令控制气动阀的动作.采集气动阀的控制指令、阀位反馈以及流量信号,采样间隔为1 s,故障模式为恒增益故障.开环状态时,利用气动阀在0~100%的指令下采集的流量变化信号,绘制流量特性曲线如图4所示,其中实线代表真实的特性曲线,虚线代表使用本文算法构建的动态模型.模型指标阈值为0.002,初始特征区间长度为样本总数.

图3 水箱实验装置Fig.3 Experimental device for water tank

图4 水箱实验执行器流量特性曲线Fig.4 Actuator flow characteristic curve in water tank
液位设定值为r=2 sin(0.01t)+94时对应的闭环系统中的气动阀信号如图5所示.其中在第201 s加入了持续100 s的增益故障.使用动态模型构建训练集,同时利用KPCA,KNMF与本文算法进行对比实验,检测效果及各项指标如图6和表3所示.本文算法能够准确判断执行器在第201~300 s之间的故障情况,而对其余时间内执行器的动态调节过程没有发生误判.KNMF的SPE统计量对处于动态调节的非故障过程存在大量误报,KPCA的SPE统计量也有少量的误报,这两种算法对执行器的动态过程的特征提取不够充分.由实验结果可知,本文算法全面优于其他两种方法,保证了及时性和准确性,同时KRNMF算法具有强大的特征提取能力,可以克服非线性和动态特征的影响,具有很高的应用价值.

表3 水箱实验中各算法性能指标Table 3 Performance indexes of each algorithm in water tank

图5 水箱实验气动阀信号Fig.5 Pneumatic valve signal of water tank experiment
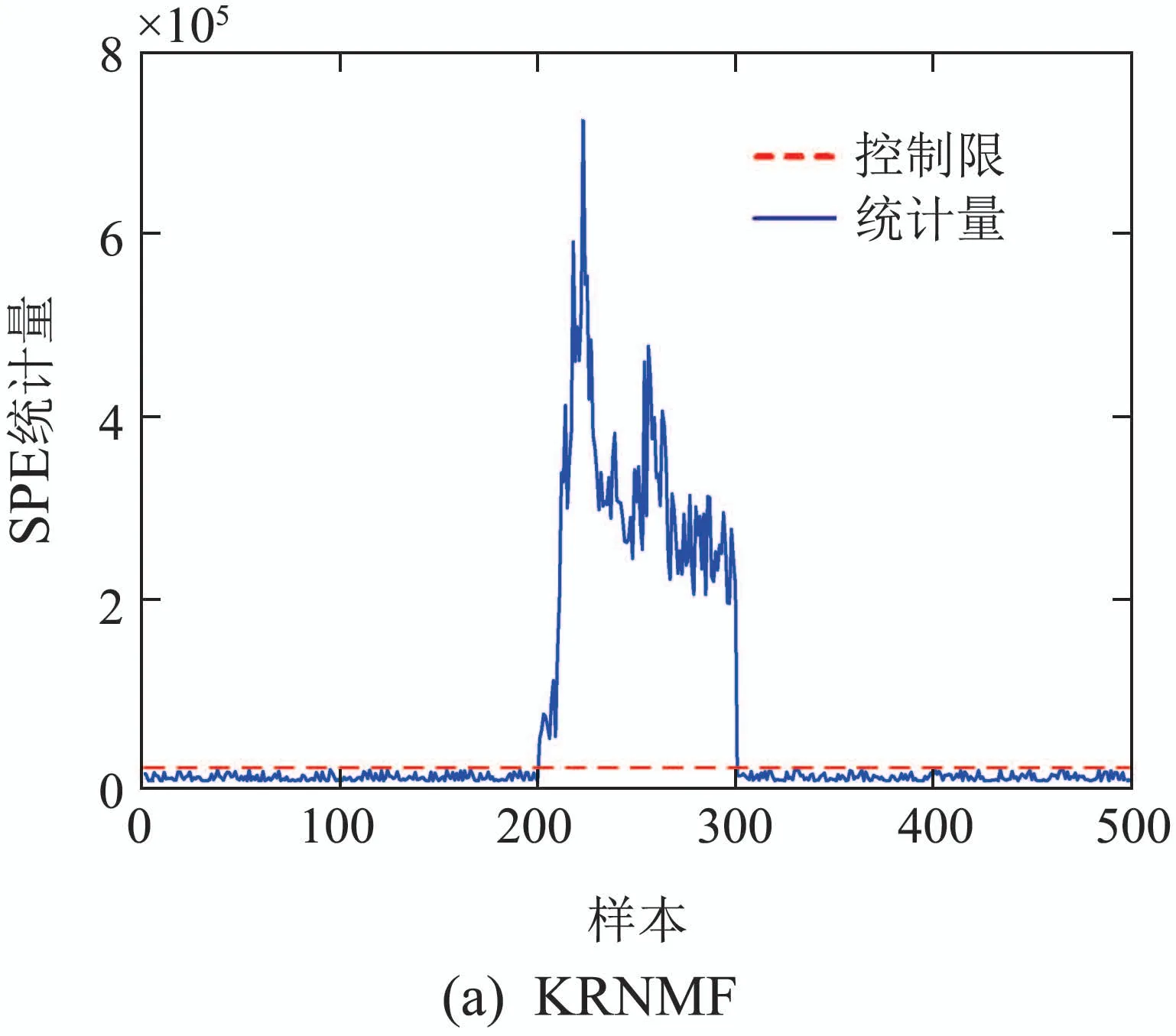

图6 水箱实验中的故障检测效果Fig.6 Fault detection effect in water tank experiment
5.3 火电厂减温水调节阀实例
本节以火电厂减温水调节阀数据为例,验证本算法的正确性.大修后的机组处于良好的工作状态中,认为此时无故障,而检修前的调节阀由于长期使用等原因势必会出现劣化,认为此时的调节阀是有故障的.使用检修后的数据建模,绘制流量特性曲线如图7所示,模型指标阈值为0.002,初始特征区间长度为样本总数.分别使用检修后和检修前的数据测试3种算法的检测效果.

图7 减温水调节阀流量特性曲线Fig.7 Flow characteristic curve of desuperheater control valve
检修前后对应的调节阀信号如图8所示.3种算法检测结果如图9、表4所示.检修后调节阀无故障时,KRNMF算法精确度最高,误报率为0,而KNMF 和KPCA算法均有较高的误报率.检修前的调节阀处于故障状态,同样的,KRNMF算法的检测率最高,而其他两种算法几乎不能检测出故障.
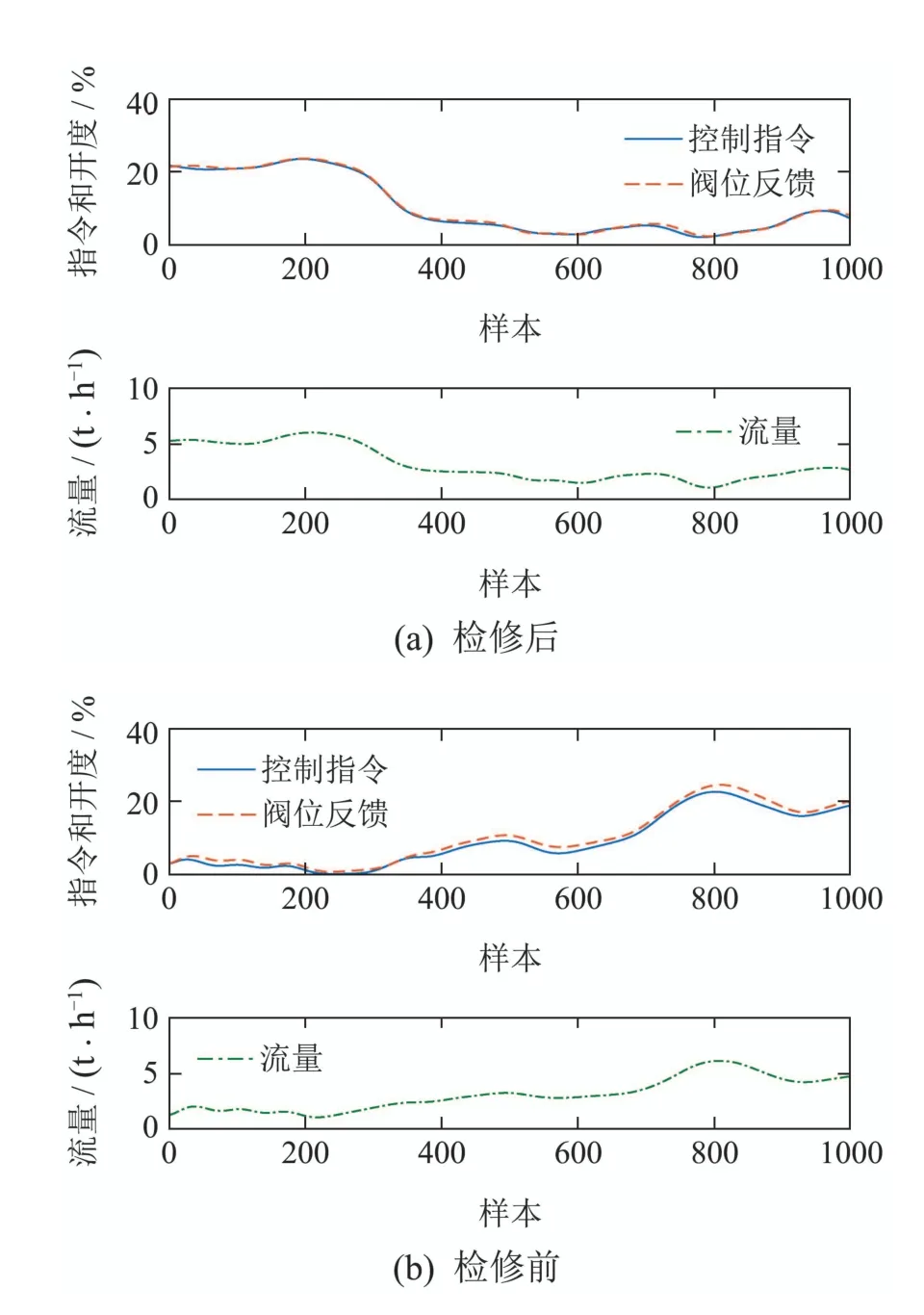
图8 检修前后调节阀信号Fig.8 Signal of valve before and after maintenance

图9 检修前后各算法检测效果Fig.9 Detection effect of each algorithm before and after maintenance
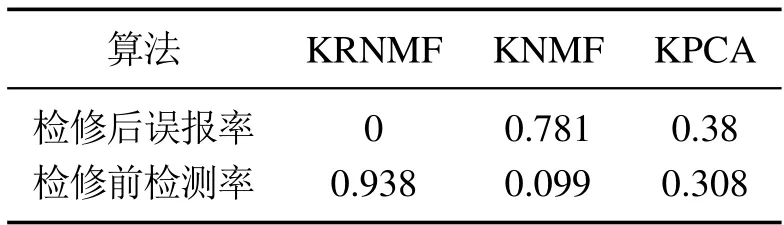
表4 算法效果对比Table 4 Comparison of each algorithm effects
由各项结果可知,在减温水调节阀的实际数据实验中,本文提出的KRNMF算法具有最高的检测率和最小的误报率,同时能够如实反应检修前后调节阀的真实状态,对实现工业过程中执行器的精准故障检测,特别是处于动态调节下的执行器,具有一定的指导意义.
6 结论
本文提出了一种新的基于核鲁棒非负矩阵分解的执行器故障检测方法.该方法构建了完备的动态工况训练集和新的监测统计量,实现了执行器动态调节过程中的故障检测,既考虑到了运行数据的非线性特性,也能够克服执行器动态变化的影响,并且通过引入误差矩阵,提高算法的抗干扰能力.相较于传统的故障检测方法,本文算法具有较强的提取能力,可以挖掘出执行器动态调节过程中存在的故障特征.通过基于DAMADICS平台、水箱平台和火电厂减温水调节阀实际数据的对比实验,充分表现了本文算法在执行器故障检测中的优越能力.
