专家监督的SAC强化学习重载列车运行优化控制

2022-06-21李中奇付雅婷

控制理论与应用 2022年5期

杨辉,王禹,李中奇,付雅婷,谭畅

(华东交通大学电气与自动化工程学院,江西南昌 330013;江西省先进控制与优化重点实验室,江西南昌 330013)

1 引言

目前为止中国铁路电气化里程已超过10万公里.作为货运专线铁路的顶级种类,重载铁路是大宗商品的运输的重要渠道,从大同出发到秦皇岛的大秦铁路更被誉为能源运输的大动脉.由于重载列车牵引质量大、编组长和线路复杂等特点,如何安全、稳定的控制列车运行得到了广泛的研究.目前研究列车智能驾驶的主流方法主要有经典智能决策算法、监督学习决策算法和强化学习决策算法.

在经典智能决策算法的思想中,多数是按照设计行驶曲线结合控制算法对列车进行控制.ZHANG等[1]以带有电控空气制动系统的重载列车为研究对象,优化重载列车的空电联合制动为目标,考虑列车安全、高效和节能因素,建立并优化了列车多质点模型,提出了长远距离运输的模型预测控制方法.TANG[2-3]使用鲁棒控制器,针对高速列车的非线性,列车质量、参数的不确定性等问题,进行速度跟踪控制使列车平稳运行.何之煜[4]利用基于迭代学习控制的自适应控制算法研究了高速列车在时变扰动情况下的追踪控制,得到跟踪精度高、收敛速度快的控制效果.

在监督学习决策算法的研究中,王悉在文献[5-6]中对数据不平衡下的重载列车智能操控的研究,利用EasyEnsemble的思想对数据样本进行随机欠抽样,再使用(K-nearest neighbor,KNN)算法对数据进行降噪处理,使重载列车能够在缺少足够类型的样本数据的情况下对列车进行稳定操控,掌握真实行驶数据情况下,能够使机器学习的算法更加可靠,减少因缺少数据产生的偏差.

在强化许学习决策算法的研究中,WANG[7]利用Q学习方法对多质点的重载列车在大下坡的情况下进行了训练,并在固定容量的Q表下对计算消耗进行了优化,完成了其最小化纵向车钩力,准时和安全的目标;TANG[8]利用双Q表切换策略对重载列车进行控制,根据Q学习离散的控制特性,可以适用于不同档位的情况;张淼[9-10]分别提供了一种基于策略梯度和Q学习的强化学习方法,通过专家经验对高速列车运行环境约束,达到节能、准点运行的目标.

上述研究使用不同的优化控制方法从多个方面对列车控制进行优化,强化学习中的策略梯度算法为在线策略,对历史的运行数据的利用率低,智能体获得的奖励收敛会相对较慢.上述文献中的控制对象HXD3机车的控制力给定为调整档位,是离散的动作空间,Q学习的方法能够训练出较好的控制策略,而HXD1机车的控制力为给定当前控制力的百分比,是连续的动作,使用Q学习的方法无法给出精度较高的控制策略.

针对强化学习在线与离线策略的问题,最大熵框架提供了一类能够高效稳定训练的算法[11],本文采用具有稳定的训练过程、能在连续动作空间上训练并有效利用智能体经验数据的(soft actor-critic,SAC)算法[12]架构,结合钩缓约束和常用空气制动,对多质点重载列车模型的运行划分成启动牵引、巡航、停车制动3个工况,分别训练,并加以专家经验对强化学习过程进行监督,得到最优的重载列车控制策略.控制的效果满足安全、稳定、高效的要求.

2 重载列车数学模型

通过对重载列车进行机理建模,搭建出重载列车的运动学模型和车钩力计算方法.模型搭建完成后将作为强化学习的环境的一部分,支持后续控制器的训练.下面对重载列车运动学建模过程进行详细介绍.

2.1 重载列车多质点纵向动力学模型

单元万吨重载列车由一辆重载机车在头部牵引,后方通过车钩连接挂载105辆货运车辆组成,列车动力单元集中在头部机车.图1为列车的机车与货车在上坡时的受力情况,可得重载列车的纵向动力学方程为

图1 多质点列车受力示意图Fig.1 Schematic diagram of multi-mass train force

其中:mi为第i辆车的质量;为第i辆车的加速度;FT为机车牵引力;Fe为机车电制动力;Fi−1为前车钩力;Fi+1为后车钩力;Fpne为空气制动力;Fw为车辆运行基本阻力;FR为列车的附加阻力,并且列车的附加阻力由线路弯道附加的弯道阻力、线路坡度造成的坡度阻力和列车通过隧道时的阻力构成,表达式为

其中:FRc为曲线附加阻力,FRi为坡道附加阻力,FRt为隧道阻力.

HXD1型机车牵引制动特性受到机车黏着力和牵引电机功率联合限制,其牵引制动特性曲线呈现分段式变化,最大牵引/制动特性式分别为式(3)-(4).其牵引制动的上限是设计控制器所需的重要约束,牵引特性与制动特性分别为

其中v表示列车的速度km/h.

2.2 钩缓装置模型

为了计算多质点受力式(1)中的车钩力大小,需要对重载列车的钩缓装置进行建模.根据文献[13]中研究的缓冲器特性对纵向冲动的影响,精确描述缓冲器的模型有重要意义.本文参考付雅婷[14]的钩缓装置建模过程,使用考虑钩缓切换速度的重载列车钩缓装置模型计算每节列车间的车钩力大小.车钩缓冲器的数学特性通过式(5)-(6)表示.

式中:FC为通过钩缓特性计算出的车钩力,其值便用作式(1)中Fi−1与Fi+1;fu为加载时缓冲器的阻抗力;fl为卸载时缓冲器的阻抗力;f3为缓冲器阻抗力均值;Δv为相邻两车速度差;Δx为相邻两车的运行距离差;ve为缓冲器转换速度.

2.3 空气制动力计算

为了计算多质点受力式(1)中的空气制动力Fpne大小,需要对重载列车空气制动系统进行建模.重载列车空气制动系统由牵引机车的总风缸、列车管与货车上的副风缸等机构构成.当重载列车发出空气制动信号时,总风缸与连通的列车管内的压缩空气向大气排出一部分,当列车管内气压降低时,置于货车上的副风缸和列车管形成压力差,将货车上的闸瓦压挤压向轮毂产生制动力,此过程称为列车空气制动.当不需要制动时,位于机车上的空气压缩机向总风缸内充气,提升列车管内的气压,将副风缸与列车管的气压差逐渐降至零,此过程称为空气制动的缓解.

根据《列车制动》[15]内容,列车常用制动的计算式为

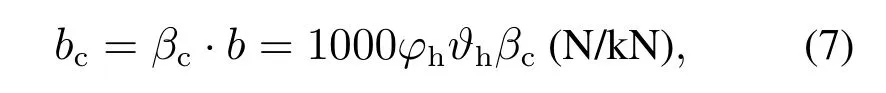
本文只考虑常用空气制动,故Fpne=bc,其中βc为常用制动系数,表1给出了部分常用制动系数,bc为列车单位制动力,φh为换算摩擦系数,ϑh为列车的制动率,b为紧急制动力.

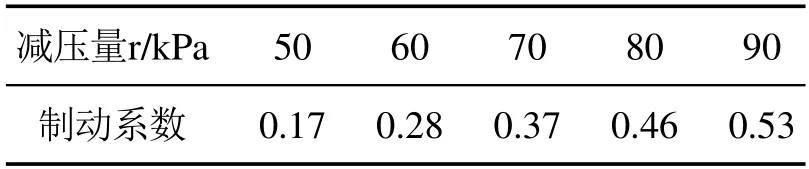
表1 部分常用空气制动系数Table 1 Partial common air brake coefficent

大秦线上的重载列车采用高摩合成闸瓦,换算摩擦系数为

2.4 翟方法多质点状态更新

为了计算出每个时刻的车辆受力,需要对多质点的速度与位移进行更新.重载列车对算法的实时性有较高的要求,设计控制算法要求算法能够在160 ms内迭代更新一次.本文采用翟方法[16]显示数值积分算法对列车非线性动力学方程(1)进行迭代运算,计算每个质点当前的速度与位置:将160 ms等分成100个小步骤进行迭代积分,满足毫秒级的计算时间与高精度要求.翟方法更新速度与位置如式(9)所示:

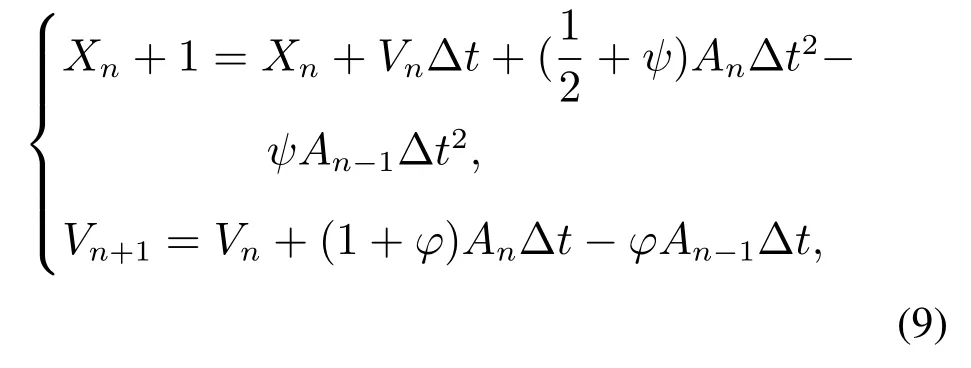
式中:Xn+1为车辆下一时刻位移量,Xn为车辆当前时刻位移量,Vn+1为车辆下一时刻速度量,Vn为车辆当前时刻速度量,An为车辆当前时刻加速度量,An−1为车辆上一时刻加速度量,Δt为时间积分步长,下标n −1,n,n+1分别代表上一步t=(n −1)Δt时刻,当前t=nΔt时刻,下一步t=(n+1)Δt;ψ,φ是控制积分方法特性的独立参数.

3 重载列车的强化学习优化控制方法

为简化控制模型设计,本文使用无模型的强化学习方法训练列车控制器.另外,为了让强化学习训练的更加快速稳定,本文通过克隆专家行为对强化学习的训练过程进行监督.下面对专家行为克隆和列车控制器的训练进行详细阐述.

3.1 RNN网络克隆专家行为

行为克隆是模仿学习中最简单的一种方法,利用神经网络将环境状态到动作的映射学习出来,把状态作为特征,动作作为被预测的值.由于重载列车具有非马尔可夫特性,本文采用循环神经网络对专家行为进行克隆.

循环神经网络(recurrent neural network,RNN)是一个具有时间动态行为的神经网络.在重载列车人工控制时,列车乘务员在驾驶列车时的手柄给定位置具有明显的时间动态过程.采用RNN网络结构对乘务员操作数据进行学习,意从经验控制数据中学习到某段区域的牵引制动时机以及控制力给定大小.通过训练出符合驾驶员操作习惯的RNN网络作为指导专家,用作强化学习控制网络输出的监督,加速智能体的训练.

专家网络的模型结构为多输入单输出的RNN模型.根据专家经验,专家网络输入为最近50个时间步长(8 s)的列车状态、动作序列,每个时间步的参数为当前时刻列车的速度、位置,输出为当前时刻采取的动作.

3.2 基于专家监督的SAC算法

本文采用SAC算法[13]架构,对重载列车控制器进行训练.该算法是面向最大熵的强化学习开发的一种离线策略算法,本文的训练过程如图2所示,主要由强化学习网络、重载列车运行仿真环境和记忆库组成.强化学习网络利用列车当前的状态输出控制指令,重载列车运行仿真环境由第2节介绍的重载列车机理模型构成,仿真环境接受控制指令输出列车的状态以及奖励作为下一时刻强化学习网络控制器的输入,并存入记忆库中以供网络学习时调用.在训练控制器参数时,通过从记忆库中采样数据分别输入到强化学习网络与专家网络中,通过专家的输出监督强化学习网络的学习.

图2 重载列车强化学习过程Fig.2 Reinforcement learning process of heavy haul train

SAC算法的最优策略表达式由式(10)表示,描述了最优策略跟奖励与熵值之间的关系,最优策略分为奖励和熵正则化项,在训练初期的策略随机,获得的奖励小,通过增加熵值可以探寻更好的策略;随着获得的奖励变大,应当将熵值减小使好的策略能够保持,直至训练末期,收获最大的奖励与最小熵,获得稳定的最优策略.

其中r(st,at)为当前重载列车运行状态下采取控制指令的奖励;H(π(·|st))=Ea～π(·|s)[−log(π(a|s))]表示动作的熵值,熵值前面的系数α为温度系数,控制着控制指令的随机性,温度系数α越大则控制指令越随机,更有利于重载列车运行状态空间的探索.每个时刻的状态与动作组合在一起形成了一条轨迹,对该轨迹求最解大的期望就是期望得到的最优策略.

强化学习中Critic网络计算损失常用的是时间差分(temporal difference,TD)方法,该方法计算开销小,且无需系统模型,网络可在状态和奖励返回后立即更新.Critic网络的损失由式(11)给出,其中TD学习表达式中的Qtarget中下一步的Q值在SAC算法中替换成了价值函数.

其中:γ为折扣因子,为target critic网络输出的Q值减去熵值,target critic网络和Critic网络结构相同,但是参数更新滞后Critic网络.SAC算法中有两个Critic网络,在训练时选取最小的Q值作为Qθ(st,at),减少过估计.

本文采用两种损失函数同时训练Actor网络:一种由Critic网络输出的价值对Actor网络进行训练,期望动作价值最大化;另一种由专家网络在相同环境状态下输出动作,与Actor网络输出的动作的均方差损失来训练,以期训练出与专家相似的决策.

评判网络对策略网络的损失由式(12)给出,

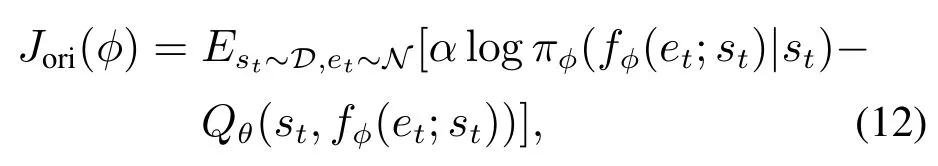
其中:πφ是根据fφ隐式定义的,fφ(et;st)为重参数化后的控制指令,帮助网络将误差反向传递;是从固定分布(如球形高斯分布)中采样的噪声.

专家网络对策略网络的损失由式(13)给出

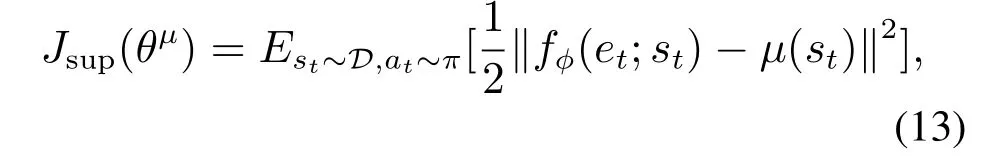
其中:µ(st)为专家网络在当前状态st下输出的控制指令;fφ(et;st)为控制网络在状态st下输出的控制指令,通过计算二者的均方根误差作为专家的监督损失;D,π为状态、策略的空间.

将评价网络输出对控制网络的损失和专家网络输出对控制网络输出的损失乘上比例系数之和得到控制网络的综合损失,如式(14):

其中比例系数在智能体找到一条能够完整完成任务的控制策略之后,将逐步递减,以实现优化目的.

温度参数决定了熵的大小,在训练过程中需要自动调整温度参数使模型可以稳定训练,所以将温度参数作为约束对象,当作一个优化问题:最大化期望收益的同时,保持策略的熵大于一个阈值.需要优化的表达式如式(15)所示:

3.3 状态空间设计

考虑到万吨重载列车由一组车头牵引着105辆货运拖车组成,而且每一个训练周期都有多个状态转移的步骤.为简化计算复杂度,本文状态空间只包含速度与位置,表示为式(17)

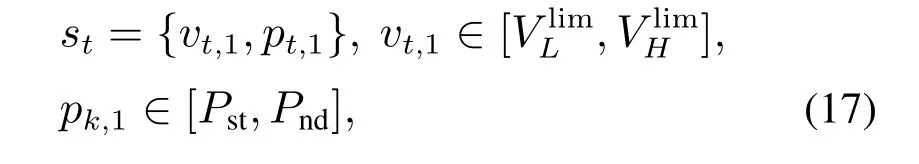
其中:st为t时刻智能体所处的状态,vt,1表示t时刻头部机车的速度,pt,1表示t时刻头部机车所处的位置.分别表示速度的下限与上限,Pst,Pnd分别表示列车的起始位置与结束位置,限速根据路段和运行时间变化,列车的起始与终结位置则根据训练功能进行调整.t=1,2,···,Ndone,Ndone为触发了终止条件的时刻.

3.4 奖励设计

好的奖励能够帮助智能体学习,稀疏的奖励会使智能体在抵达目标前无法获得任何奖励,加大训练难度,奖励分布的方差太大也会使得策略梯度太大导致学习不平稳,将奖励归一化能够有效提升学习效率.

虽然强化学习的本质就是积累奖励使奖励最大化,奖励的设置与要实现的目标有很强的关联性,负奖励有利于有限步数内快速结束该回合,正奖励鼓励智能体不断累积奖励以维持最高奖励状态.

3.4.1 速度奖励设计

智能体学习操控列车有两种目标:在启动至巡航阶段,应当获得正奖励以累积奖励值,鼓励智能体将奖励最大化;而在制动过程中操控的目标是在安全操纵下停在指定地点,这时应该将奖励设计为负值,以期智能体快速达到目标状态.本文将速度奖励设计为式(18)

图3 速度距离相关奖励Fig.3 Speed-distance reward

图3为机车速度、机车与下一个站点的距离有关奖励的等高线图,预设为距离终点2 km处速度上限开始下降,分界线右侧为当最高限速为80 km/h时,速度的奖励距离终点2 km外启动牵引和巡航工况的速度奖励,红色越深则奖励值越大.

为加快算法的训练速度,对目标探索空间进行约束.参考TANG[8]的奖励设置,给定了智能体探索的上限与下限.上限为机车满级位运行的速度-位移曲线,下线为以初始40%牵引力,每隔200步递减1‰的牵引力运行的速度-时间曲线,对超出期望探索范围的状态-动作进行惩罚.

3.4.2 车钩力奖励设计

列车运行过程中,车钩力应当在最大应力极限范围内变化,以免造成脱钩事故.为避免智能体一直施加最小的控制力,本文将车钩力的奖励函数进行分段处理,在正常车钩力范围内奖励函数为定值,当车钩力大于1000时,车钩力奖励逐渐下降.最大车钩力的奖励rc构造为式(21)

其中maxFc为整列车的最大车钩力,车钩力的奖励是将最大车钩力约束到[−1,1]的区间内.

3.4.3 控制力变化奖励设计

车钩力的约束仅在重载列车产生了较高的车钩力时做出惩罚,为了能够获得一个更为平稳的控制策略,本文对控制策略进行了约束,如式(22):

其中:F为当前控制力,F′为上一时刻的控制力,如果当前控制力与上一时刻的控制力差值在50 kN以内,对智能体给出奖励,否则惩罚智能体的该动作.

为了将上述奖励函数都发挥作用,达成多目标优化的效果,将上述多个目标的奖励线性组合为单个目标奖励以方便目标优化.奖励的形式为式(23)

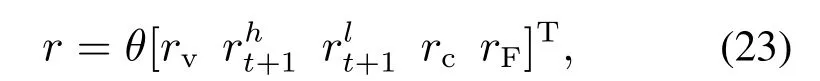
参考DSQ方法控制重载列车[8]的奖励参数分配,并且结合本文定义的奖励对象,本文各奖励参数分配分别为θ=[3 1 1 1 1.5].

3.5 记忆库采样

在SAC算法中需要引入记忆库存储智能体经验数据来训练智能体.记忆库的保存方式为(s,a,r,s′,done,period),保存与环境互动产生的当前状态、采取的动作、获得的奖励,下一时刻的状态、回合终止标志和每个动作状态对应的周期.

由于专家网络输入为时序结构,数据采样需要做预处理,满足采样表示的准确度.获取记忆库索引,并且初始化采样计数器.在当前索引基础上递归向前收集数据,若采样计数器到达50时,则采样结束;若采样计数器为i(i ＜50)且到达该数据周期头部,则在该采样数据头部在添加(50−i)个零,以补全50个数据,以提供专家策略网络输入.

4 实验与分析

由于线路区段较长,训练全程的操纵计算的开销非常大.本文将整个驾驶过程分为3种情况:启动阶段、巡航阶段、制动阶段,3段控制的位置为同一区间的连续3段分别为:24～44 km,44～83 km,83～88 km.通过在3个工况分别训练相应的控制器,减少训练需要的计算消耗.

4.1 RNN专家网络拟合

为得到一个具有鲁棒性的预测模型,在专家经验数据中添加高斯噪声,训练后的专家模型克隆效果如图4所示.从图中结果看,训练后的模型能够很好的拟合专家操控策略.

图4 RNN拟合专家控制效果Fig.4 RNN fitting expert control performance

表2中给出了对重载列车行为克隆之后的专家网络与原始的专家经验之间的误差.3个运行阶段的控制力的误差控制在3%以内,误差最大仅有21.63 kN.对列车的控制来说,无特别影响.

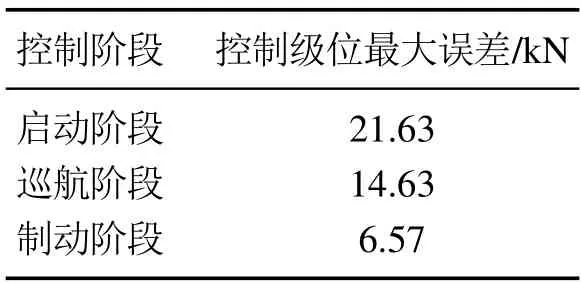
表2 专家控制力拟合误差Table 2 RNN fitting error of expert control force

4.2 专家监督的SAC强化学习训练

为了使训练后的3种控制器能够联合使用,让重载列车能够完整的运行,本文在训练巡航和制动时将对列车初始速度在60～80 km/h的范围内进行一个随机初始化.本文SAC+EXPERT模型相关参数列于表3中.

表3 模型相关参数Table 3 Module reference parameters

根据图5中3个阶段训练奖励变化的结果,可以看到在本文提出的SAC+EXPERT算法训练获得的奖励都高于SAC和DDPG两种算法,在训练的稳定性方面,通过多次在环境种迭代训练之后,本文的SAC+EXPERT算法训练的奖励收敛的也都更加稳定,波动较小.

图5 各阶段训练奖励变化Fig.5 Reward evalution in three operation training

为了训练一个能够进行巡航制动切换的控制器,同时参考实际工程环境,本文选择距离停车点5 km处作为制动阶段的起始点来训练制动控制器,并设定重载列车停在终点300米以内算作精准停车.

图6-8中的(a)图为SAC+EXPERT和SAC两种算法在启动牵引、巡航控制、停车制动3种工况下控制后得到的速度-位移曲线与对应的控制力曲线.通过上述3张图可以看出本文提出算法训练出的控制器在3个阶段的平均速度都比较高,3个阶段的运行效率分别提高了16.75%,1.88%,11.18%,明显的提高了重载列车的运行速度.在巡航工况下,本文方法训练出的智能体级位的变化更加平缓.在制动阶段,停车位置距离目标停车点300米以内,达到了预设的停车目标区间.

图6 启动阶段控制效果Fig.6 Performance of control in startup step

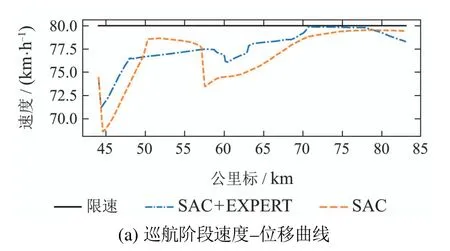
图7 巡航阶段控制效果Fig.7 Performance of control in cruise step

图8 制动阶段控制效果Fig.8 Performance of control in brake step

图6-8中的(b)图为启动牵引、巡航控制、停车制动3种工况下的控制力变化曲线.用本文方法训练出的控制器在启动和制动阶段没有出现明显的抖动,训练出的控制器具有专家控制器的部分特征.巡航区间中受到专家监督的SAC算法的控制器波动更小,控制更加稳定.在制动阶段,训练出的控制器能够实现通过电制动减速,并使用空气制动辅助停车的操作方法.

最后,本文试验了长大下坡路段的循环制动控制,效果如图9所示.根据图9(b)(c)(d)中的控制力、目标管压变化以及最大车钩力曲线中,SAC 与SAC+EXPERT的运行效果均在车钩最大承受范围内,较为平稳运行.在运行效率上结合图9(a)中的速度变化曲线,带专家监督的SAC策略比SAC的策略高出4.33%.