矿体回采爆破对覆压铁路安全性的数值模拟研究*

2022-06-21褚夫蛟段玉德李公成王作鹏魏志鹏张连新

爆破 2022年2期

褚夫蛟，段玉德，李公成，王作鹏，魏志鹏，张连新

(1.山东理工大学资源与环境工程学院，淄博 255000；2.山东东平宏达矿业有限公司，泰安271000；3.山东盛鑫矿业有限公司，泰安 271000)

如今大多数金属矿山采用爆破的方式进行开采，但是，炸药在爆炸时会产生巨大的能量，其中一部分能量会以地震波的形式传播到地面，在爆区范围内，会对地面建筑设施的安全产生影响[1,2]，因此，正确的评估爆破时对地面建筑设施的影响是十分重要的。

目前，地下矿山爆破时对地面建筑的安全影响引起许多学者的关注，陈永伟通过三维动力数值及萨道夫斯基经验公式计算得出路堑开挖爆破时对铁路路基的质点峰值振动速度的最大值[3]，根据经验公式与数值计算得到的质点峰值振动速度均小于规程，可以保证既有铁路路基安全。V Graizer认为[4]，低速率带和地质地貌是振动放大效应的主要原因。S Spyros等利用有限元程序模拟软件模拟了爆破振动波在地形中的传播[5]，获得了到达时间以及域内特定点的正负相位持续时间关系；孙秀民等根据路堑边坡及现场爆破振动所测得的数据[6]，经数学回归分析处理，得到爆破震动传播经验公式，根据所得公式计算出不同距离出的建筑物振动速度，参照相关规程对爆破时周围民用建筑的安全进行评价，同时给出了爆破振动安全的允许距离。J Torano等综合考虑不同介质、装药量、起爆顺序等因素[7]，通过建立三维有限元模型研究了隧道爆破振动速度分规律。叶明班等基于背景工程结合岩质边坡下部台阶爆破开挖进行现场振动监测[8]，建立了岩质边坡动力响应数值计算模型，系统分析了边坡岩体质点峰值振速、应力场及位移场的变化和分布规律。于德海等通过三维有限元程序仿真模拟以及工程现场动态监测对比[9]，研究爆破振动对既有构筑物的动力响应问题。

国内外学者在研究爆破振动对构筑物影响方面已取得了一系列成果，但是，针对地下爆破对地铁路基的安全影响所作的研究却不多。结合某矿山Ⅰ-1 矿体矿房爆破回采矿石时爆破振动对铁路安全的影响，利用三维数值模拟方法建立矿体和铁路路基的数值模型，对矿体爆破时路基的动态响应情况进行分析，获取矿房爆破时铁路路基以及车站的振动速度、路基应力以及应变等数据，分析Ⅰ-1 矿体回采爆破对既有铁路线及车站的安全影响。

1 项目概况

某矿山地形为冲洪积平原区，矿山北部约1.3 km处地表有铁路通过。矿山内矿体大部分赋存于-40 m标高以下，按矿体顺序，主要有Ⅰ-2、Ⅰ-1、Ⅱ-1、Ⅲ矿带、Ⅳ矿带。其中Ⅰ-1矿带距离北部铁路较近，最小水平距离仅327 m，如图1所示。Ⅰ-1对铁路及车站安全起主要影响，矿体设计采用分段凿岩阶段矿房嗣后充填采矿法。企业北部铁路主要考虑的影响范围为DK900+750～DK904+250。

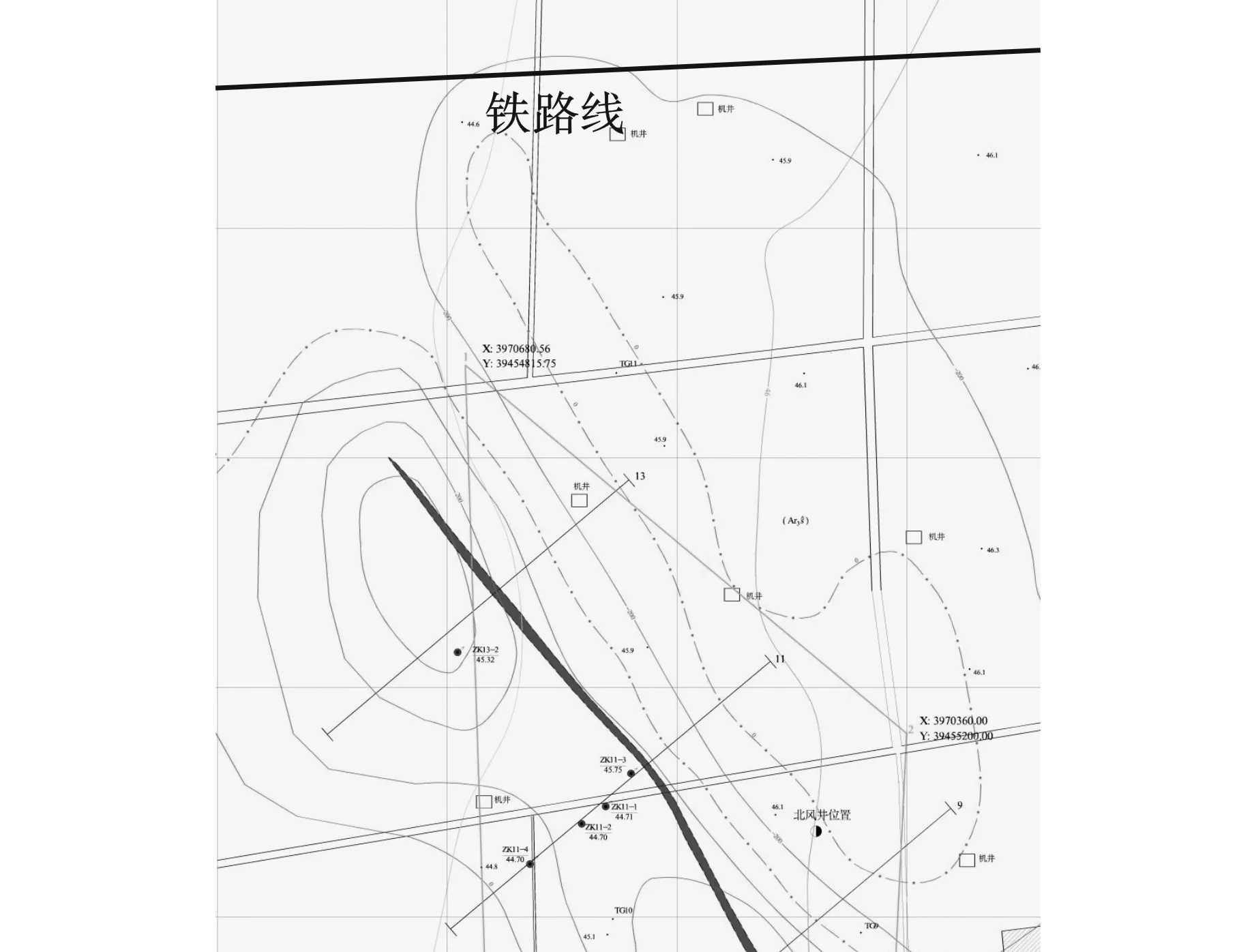
图 1 矿体与铁路位置关系图

采用地震波安全距离计算最大药量[10]。

R=(K/V)1/αQ1/3

(1)

式中：R为测点至爆源的中心距离，铁路路基按距离爆源最近距离取327 m，地表建筑按距离爆源最近距离取150 m；K、α为与介质场区条件等有关的待定常数，根据当地岩性为中硬岩石，参考类似矿山，K取200,α取1.75；V为质点最大允许速度，铁路路基取3.5 cm/s；地表建筑的村落中仍存在土坯墙，按较差民房取1 cm/s；Q为每次爆破或单段最大药量。

表 1 工业和商业建筑物爆破振动安全允许标准

采用上向扇形中深孔爆破，对矿体厚度10 m，分段高度17 m的标准采场进行布置计算，炮孔结构布置如图2所示。图中每排10个炮孔，炮孔合计129.4 m，其中最深孔19.8 m，装药长度94.5 m，装药系数0.73，其中最长装药长度15.4 m，单孔最大装药量43.6 kg，单排装药量267.4 kg。

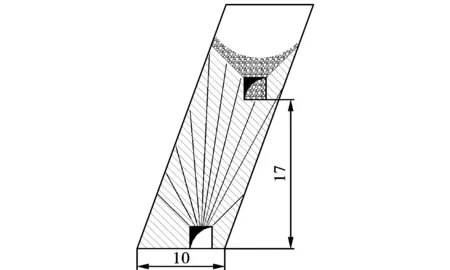
图 2 扇形中深孔结构布置图(单位：m)

注：硐室爆破f小于20 Hz，露天深孔爆破f在10～60 Hz之间，露天浅孔爆破f在40～100 Hz之间，地下深孔爆破f在30～100 Hz之间，地下浅孔爆破f在60～300 Hz之间(下同)。

由于矿房爆破回采属于地下深孔爆破，f=30～100 Hz，同时测定质点振动相互垂直的三个分量，得质点振动速度为三分量中的最大值，由表1、表2可知[11，12]，取铁路工程的爆破振动速度安全允许标准为3.5 cm/s。铁路路基从上至下由A组填料、改良土、路基本体、碎石垫层组成，根据相关资料，以各组成材料的强度作为强度标准。

2 数值模拟

2.1 计算模型和参数

2.1.1 模型尺寸和网格划分

车站是生产的基地，集中了与行车有关的技术设备，人员密集，人口流动量大，路基是轨道或者路面的基础，为列车运行提供必要条件，保证铁路路基及车站的安全是必要的，在矿房1及矿房2爆破回采矿石时，对铁路路基及车站的安全有影响，因此，数值计算以铁路路基和车站作为研究对象，选取K907+892.88(DK900+750)～K909+894.88(DK902+752)段路基以及最近距离的矿房，通过施加爆破荷载获取铁路路基的动态响应情况，建立如图3所示几何模型。距离路基最近的为矿房1，距离车站最近的为矿房2，矿房1与路基最近距离约327 m，与车站距离约为1810 m，矿房2与路基最近距离约1030 m，与车站距离约为1654 m。通过设置单元尺寸以及软件自动划分网格功能，建立数值计算模型如图4所示[13]，模型包含95577个单元，47842个节点。为最大限度获得爆破振动，从极限角度出发，减小软弱地层对爆破地震波造成的衰减作用，模型不设地表黄土层。

表 2 铁路路基相关爆破振动安全允许值

图 3 Ⅰ-1号矿体与铁路路基空间位置关系

图 4 数值计算模型

2.1.2 爆破荷载设置

目前对隧道爆破振动影响的研究中，关于爆破冲击荷载的相关参数尚无较为完善的方法和理论加以确定。结合前人研究，采用美国National Highway Institute里提及的公式[14]。爆破荷载计算公式如下

(2)

(3)

(4)

式中：Pdet为爆破压力；PB为孔壁面上的压力；PD(t)为爆破压力的时程函数；Ve为爆轰速度；dc为炸药直径；dh为炮孔直径；γ为比重；B为荷载常量。

结合矿山采矿的爆破设计方案，通过计算得到爆破时程荷载如图5，数值计算模型所用的主要物理力学性能参数见表3。

2.2 铁路路基动态响应分析

根据矿房1和矿房2的位置关系，以与两矿房邻近的铁路路基作为研究对象，同时监测车站的动态响应情况，设置1-1、2-2、3-3剖面，其中矿房1爆破时主要监测1-1、3-3剖面，矿房2爆破时主要监测2-2、3-3剖面，如图6所示。对于各剖面，设置4个监测点(如图7所示)，主要监测各点位的质点振动速度，以此来表征其动态响应情况。

图 5 爆破荷载时程曲线

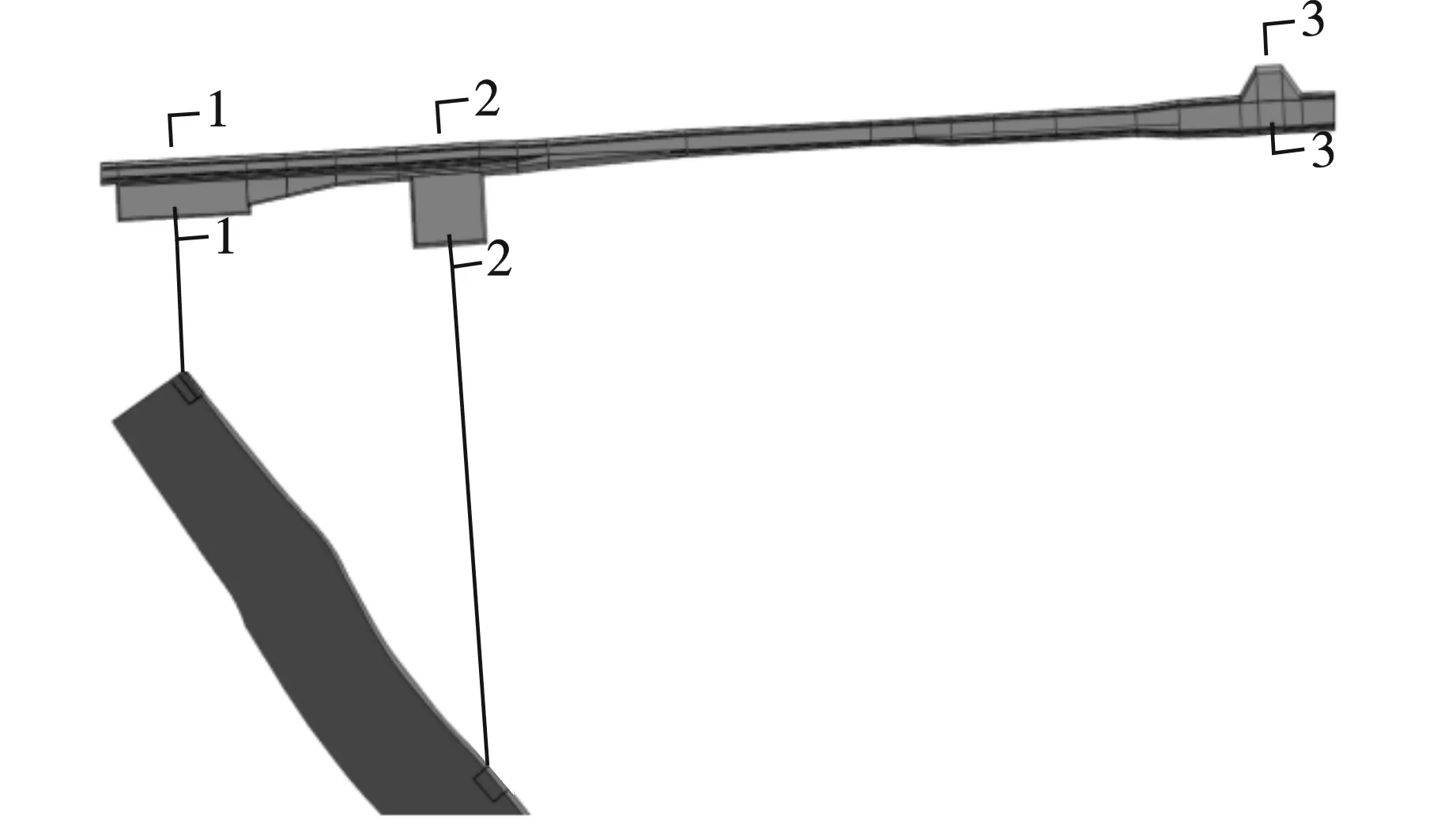
图 6 监测剖面设置

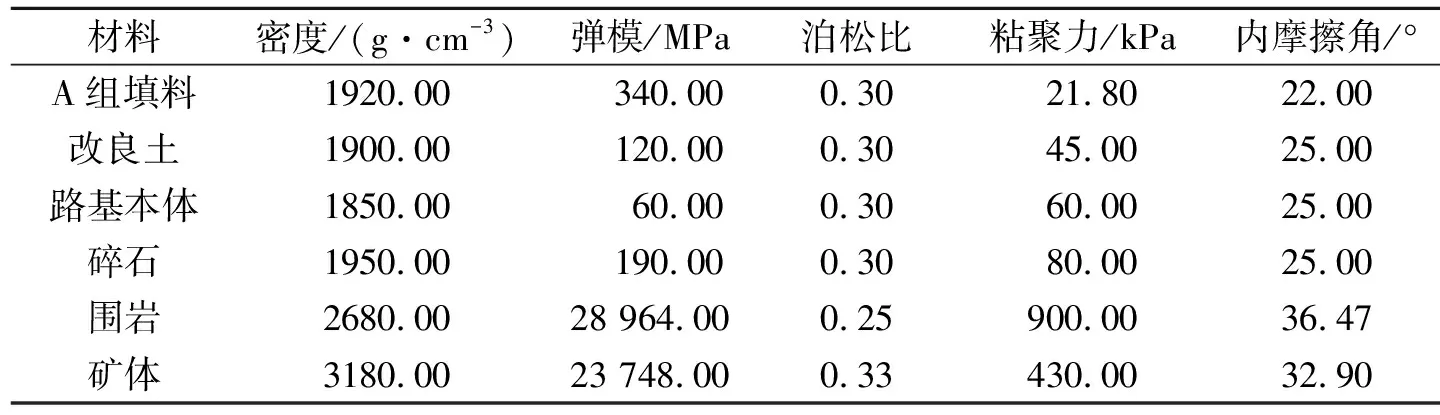
表 3 主要物理力学性能参数

图 7 剖面测点位置图

2.2.1 速度响应分析

根据《爆破安全规程》，提取各测点的振动速度峰值，见表4所示。(各测点的名称以“剖面-测点”的方式命名，如“1-A”测点表示1-1剖面的测点A)。

从表4可以看出，最大振动测点位于1-1剖面的铁路路基下部，此时为矿房1爆破导致的，最大合速度为3.412 cm/s，三向最大速度为3.392 cm/s，为Y方向，即为南北向。而1-1剖面在矿房1爆破时所有测点的最大振动速度方向均为Y方向，其数值分别为A点：2.173 cm/s，B点：3.392 cm/s，C点：2.658 cm/s，D点：2.303 cm/s。

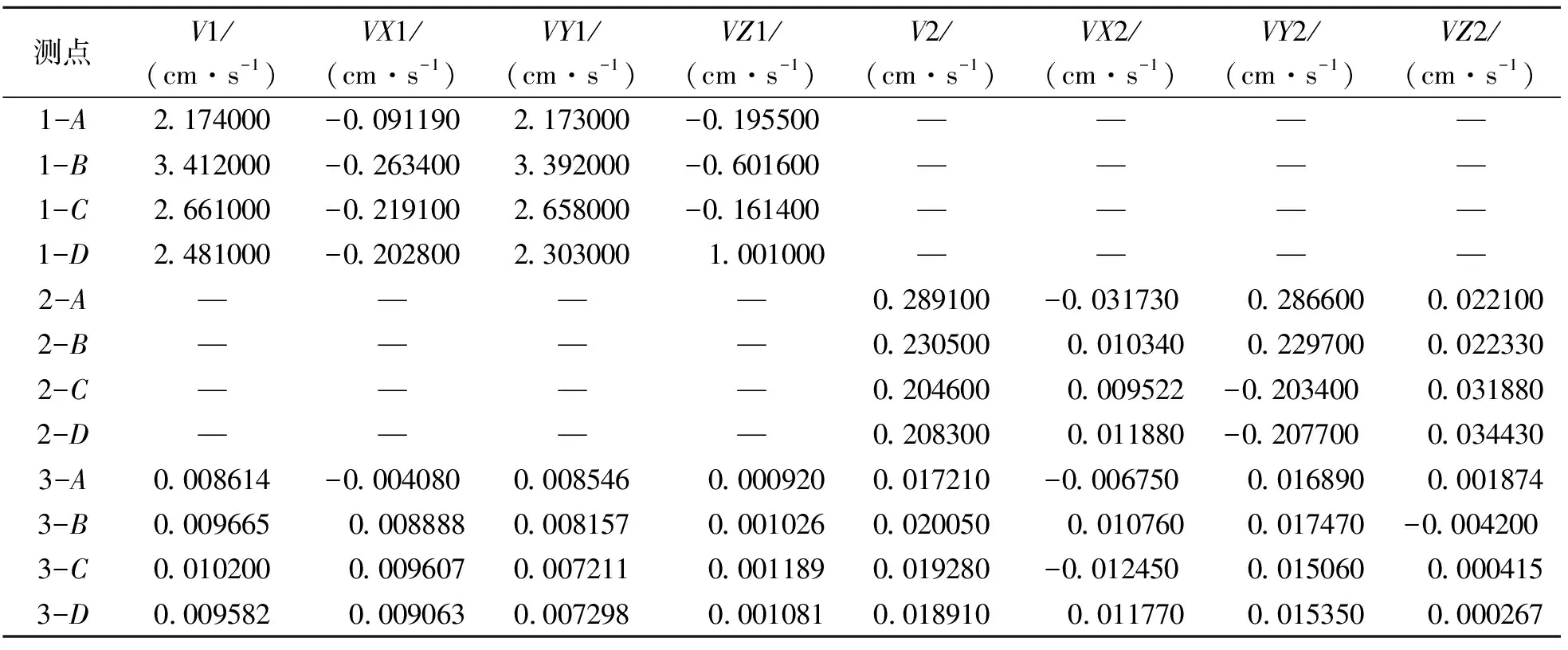
表 4 矿房1、2爆破各测点振动速度峰值(单位：cm/s)

从表4中可以看出，车站在矿房1爆破时所产生的振动最小，最大合振动速度仅为0.0102 cm/s，三向最大振动速度为X方向，仅有0.009607 cm/s。

矿房2爆破时，距离铁路路基约1000 m，为矿房1与铁路路基距离的3倍，此时导致的路基振动速度明显低于矿房1爆破导致的振动，最大合振动速度为0.2891 cm/s，三向最大振动速度为Y方向。与矿房1爆破导致的路基最大振动速度方向一致，各测点的最大振动速度方向均为Y方向。而此时矿房2距离车站约1650 m，车站的合振动速度最大值为0.02005 cm/s，为铁路路基底部振动速度。

从以上数据及分析可以看出，两种工况导致的最大振动速度出现在了矿房1爆破时铁路路基测点，最小振动速度为矿房1爆破时车站位置，各测点振动速度均小于确定的爆破安全允许质点振动速度。

2.2.2 应力分析

提取1-1剖面、2-2剖面的应力云图，如图8、9所示，各工况下应力最大值出现在了矿房1爆破时的1-1剖面，其中最大主应力最大值为8108.17 Pa，为拉应力，最小主应力最大值为12409.1 Pa，为压应力，最大剪应力最大值为5955.34 Pa，均位于非铁路路基即维修办公区域基础的底部，且最大应力值小于路基各材料的抗压、抗拉和抗剪强度。矿房1爆破时，由于车站距离较远，所产生的应力最大不超过100 Pa。矿房2爆破时，2-2剖面路基产生的应力最大值均小于矿房1爆破时1-1剖面路基所产生的应力值。而矿房2爆破时位于车站的3-3剖面应力值最大不超过150 Pa。由此可知矿房1、矿房2爆破时，路基所受的爆破冲击均小于自身强度，所受扰动较小，路基结构相对稳定。

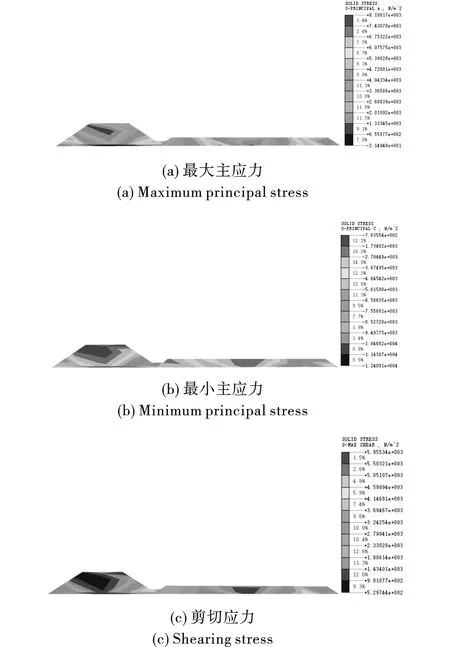
图 8 矿房1爆破1-1剖面应力云图

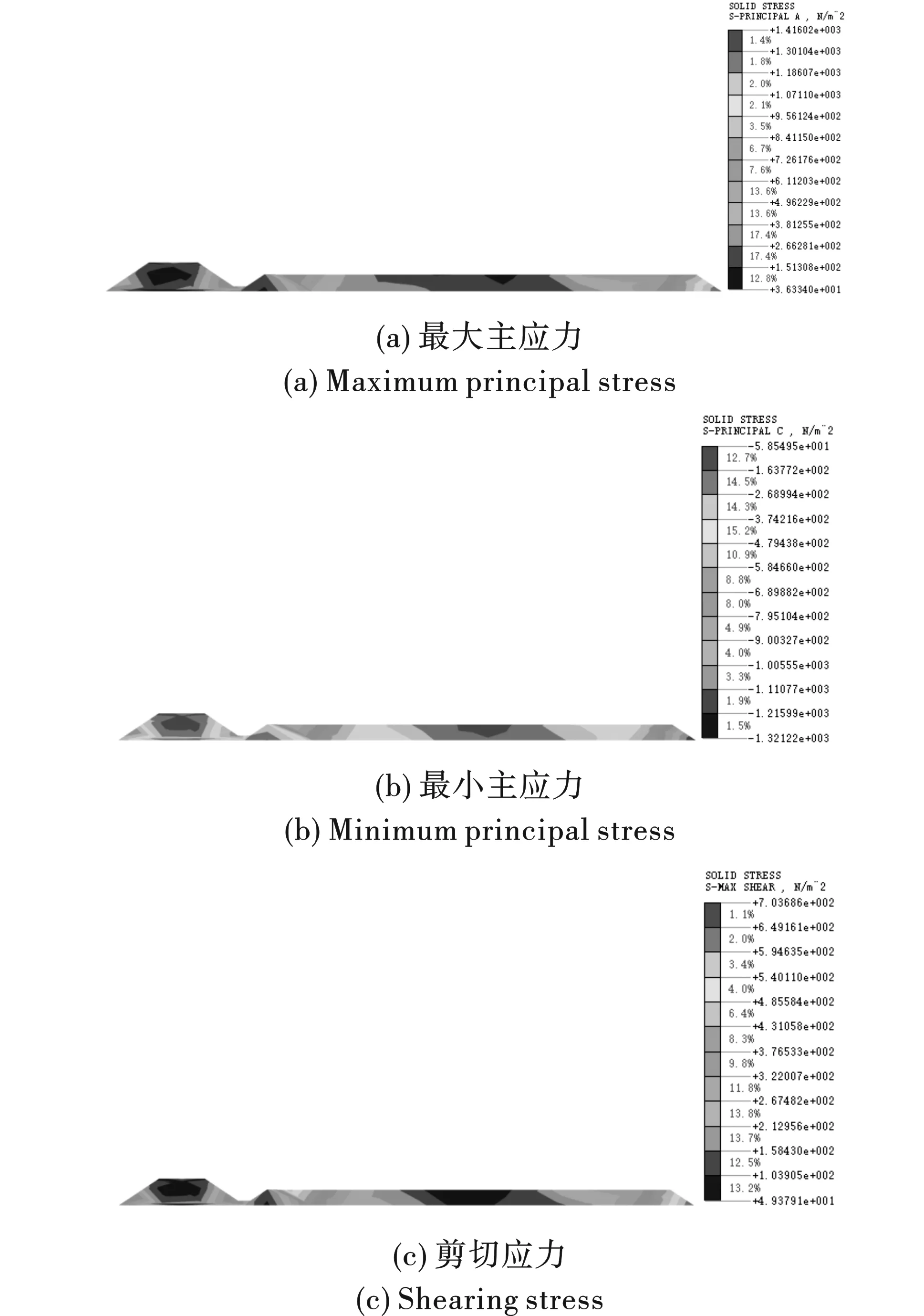
图 9 矿房2爆破2-2剖面应力云图

2.2.3 应变分析

提取不同工况下各监测剖面的应变云图，如图10所示。矿房1爆破时的1-1剖面最大剪应变值仅为2.58×10-4ε，变形较小。车站最大剪切应变值仅有1.15 με，所受影响非常轻微。矿房2爆破时，2-2剖面路基剪切应变最大值仅有30.59 με，车站的最大剪应变值仅为2.47 με，由此可知矿房1、矿房2爆破时，路基所受的爆破冲击均小于自身强度，所受扰动较小，路基结构相对稳定。