踩好得分点 考题巧解答

文／余叶军

“统计与概率”这部分内容的考查方式灵活多样，试题背景新颖，既注重对基本概念、基本方法的考查，又注重对知识本质与应用意识的考查，更渗透统计与概率这一数学思想。在中考中，此类题属于必考题，难度不大。大家在做题时往往信心满满，但由于在实际答题时对得分点把握不准，对具体分值的分配理解不够，最终会出现一些失误。因此，答题时踩好得分点是关键。要想答题得满分，大家就必须正确理解题意，写好关键步骤。

例1我市为加快推进生活垃圾分类工作，对分类垃圾桶实行统一的外形、型号、颜色等，其中，可回收物用蓝色收集桶，有害垃圾用红色收集桶，厨余垃圾用绿色收集桶，其他垃圾用灰色收集桶。为了解学生对垃圾分类知识的掌握情况，某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生，根据调查结果，绘制了如下图所示的两幅不完整的统计图。

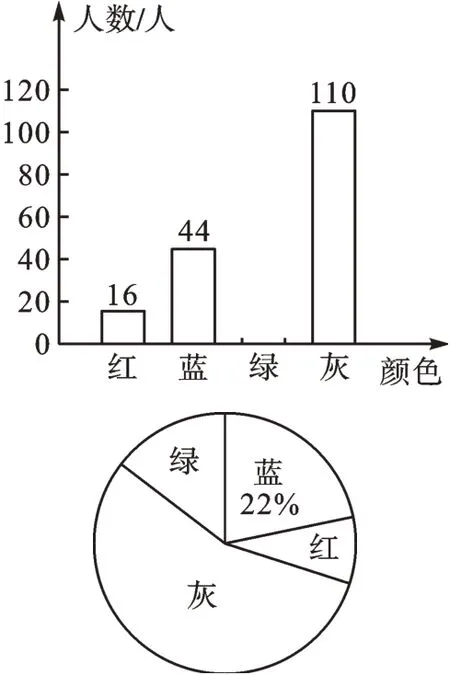
根据图中信息，解答下列问题：

（1）此次调查一共随机采访了________名学生，在扇形统计图中，“灰”所在扇形的圆心角的度数为________度；

（2）补全条形统计图（要求在条形图上方注明人数）；

（3）若该校有3600 名学生，估计该校学生将用过的餐巾纸投放到红色收集桶的人数；

（4）李老师计划从A、B、C、D四名学生中随机抽取两人参加学校的垃圾分类知识抢答赛，请用树状图法或列表法求出恰好抽中A、B两人的概率。

解：（1）此次调查一共随机采访学生44÷22%=200（名），在扇形统计图中，“灰”所在扇形的圆心角的度数为。故答案为200，198。

（2）绿色部分的人数为200-（16+44+110）=30（人）。

补全图形如下：

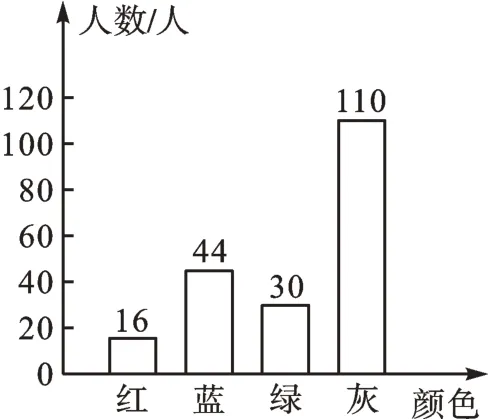
（3）估计该校学生将用过的餐巾纸投放到红色收集桶的人数为

（4）列表如下：

A B C D A（A，B）（A，C）（A，D）B（B，A）（B，C）（B，D）C（C，A）（C，B）（C，D）D（D，A）（D，B）（D，C）

由表格知，共有12 种等可能结果，其中恰好抽中A、B两人的有2种结果，

所以恰好抽中A、B两人的概率为

【点评】此类统计与概率考题一般分为3问或4 问，总分值为8 分。本题设置4 问，每问分值为2 分。如果在第（1）问就出现计算错误，那么整个题几乎就没有得分的可能，所以我们在遇到“统计与概率”这类题的时候，除了要读懂统计图上的数据，还要注重运算过程，在计算时要细心。第（4）问是对等可能性的考查，我们必须准确地画出树状图或列出表格，才能得到满分。

例2李老师为缓解小如和小意的压力，准备了四个完全相同（不透明）的锦囊，里面各装有一张纸条，分别写有：A.转移注意力；B.合理宣泄；C.自我暗示；D.放松训练。

（1）若小如随机取走一个锦囊，则取走的是写有“自我暗示”的锦囊的概率是______；

（2）若小如和小意每人先后随机抽取一个锦囊（取走后不放回），请用列表法或画树状图的方法求小如和小意都没有取走“合理宣泄”的锦囊的概率。

解：（1）若小如随机取走一个锦囊，则取走的是写有“自我暗示”的锦囊的概率是

（2）画树状图如下：

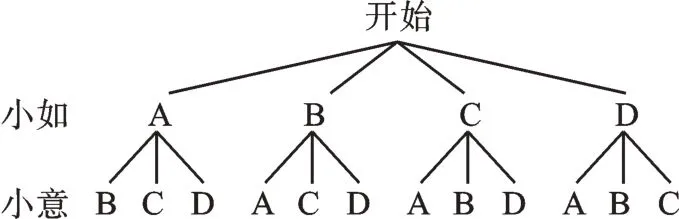
共有12 种等可能的结果，小如和小意都没有取走“合理宣泄”的锦囊的结果有6种，

【点评】此类概率考题一般分为两问，总分值为8 分。本题第（1）问为3 分，第（2）问为5分，这5分又分为画图3分和答案2分。此题的第（1）问往往得分率较高，如果出错，常常是因为审题不仔细。第（2）问的错误率较高，出错的原因往往是误认为随机抽取一个锦囊后又放回去了，而题目的意思是抽取后不放回去，由此产生了理解的偏差，导致解答错误，最终丢分。这一问的另外一种丢分情况是：虽然能够准确地画出树状图，但在最终求概率时出错。题目是要求“小如和小意都没有取走‘合理宣泄’的锦囊的概率”，但误求的却是取走“合理宣泄”的锦囊的概率，这时候就只能在画图处得分，最终的答案分就拿不到了。

因此，“统计与概率”考题的解答，只有读懂统计图，厘清题意，准确计算，画准图形，才能把握好常规得分点，拿到满分。