三问三思，火眼识“坑”

文／喻 洋

同学们在解决多解题时被“坑”过吗？多解题虽然“陷阱重重”，却时常有一些“提示线索”，答案就暗藏其中。我们只有认真审题、深思熟虑，方可理清“线索”，避免“入坑”。下面结合3 个案例，老师将谈谈解题过程中如何审慎思考、避免“入坑”。

一、分布区域清楚吗？

例1在平面直角坐标系中，x轴的上方有一点P，向左平移两个单位长度再向上平移一个单位长度后，该点到x轴的距离为7、到y轴的距离为8，则点P的坐标是________。

【错解】点P坐标为（10，7）。

【火眼识“坑”】点P与y轴的位置关系并没有被提及，所以点P与y轴的位置关系暂不清楚，需要分类讨论，答案也就不唯一。

【正确解答】因为点P平移后到y轴的距离为8，所以平移后的横坐标为8或-8。又因为点P在水平方向上向左平移了两个单位长度，所以平移前的横坐标为10 或-6。点P的纵坐标因为受条件“x轴的上方”约束只能是6，所以本题有两解（10，6）和（-6，6）。

二、对应关系明确吗？

例2如图1，点A坐标为（-2，2），点B坐标为（2，0），点C坐标为（4，2），点D坐标为（2，-2）。若线段AB和线段CD间存在某种变换关系，即其中一条线段绕某点旋转一个角度后可以得到另一条线段，则这个旋转中心的坐标是________。

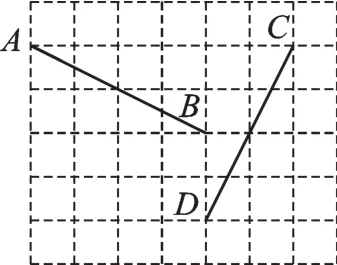
图1

【错解】连接AC、BD，作AC、BD的垂直平分线交于点M（1，-1），点M即为所求。

【火眼识“坑”】根据图形旋转的性质可知，旋转中心应该在对应点连线的垂直平分线上，其中“对应”二字尤其值得关注，但本题并未指明对应关系，故应分两种情况讨论。

【正确解答】如图2，当点A的对应点为点C时，已求；当点A的对应点为点D时，连接AD、BC，作AD、BC的垂直平分线交于点M′（2，2），点M′即为旋转中心。综上，旋转中心为（1，-1）或（2，2）。

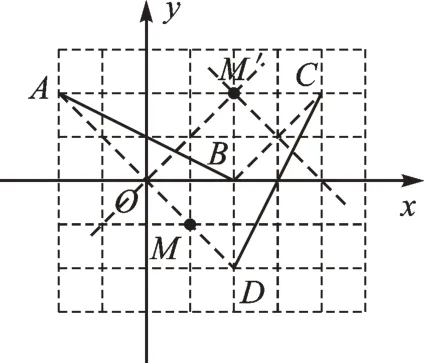
图2

三、运动位置确定吗？

例3在平面直角坐标系中，已知直线与x轴、y轴分别交于A、B两点，点C（0，n）是y轴上一点。把△ABC沿直线AC折叠，使得点B翻折后的对应点B′刚好落在x轴上，求点C的坐标。

【错解】如图3，根据勾股定理可得AB=5，再根据折叠的性质有BC=B′C=4-n，AB=AB′=5，则OB′=5-3=2。在Rt△B′CO中，利用勾股定理列出方程n2+22=（4-n）2，可以解得，所以点C的坐标为

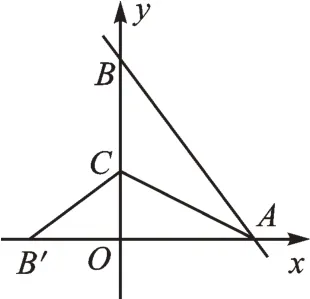
图3

【火眼识“坑”】动点C作为y轴上一点，既可以位于y轴的正半轴，也可以在y轴的负半轴，而错解只研究了其中一种情况。

【正确解答】若点C在y轴的正半轴，已求；若点C在y轴的负半轴，如图4，根据翻折的性质，有AB′=AB=5，则OB′=8，又CB′=CB=4-n，所以，在Rt△OCB′中，利用勾股定理列方程，解得n=-6，即点C坐标为（0，-6）。故答案为或（0，-6）。

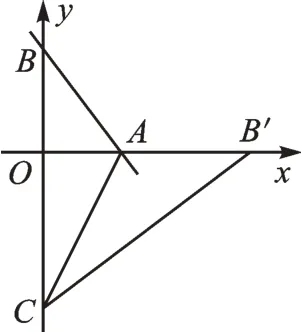
图4

有时候，问题的“线索”隐藏得巧妙，“坑”也挖得很深，但如果我们平时养成思维严谨、考虑全面的良好习惯，审慎思考，火眼识“坑”，多留意对应关系，多关注“模糊地带”，多观察运动范围，不仅会避免“入坑”，而且还会“填坑铺路”，铺就一条数学的阳关大道。