基于邻域粗糙集和帝王蝶优化的特征选择算法

孙林，赵婧，徐久成，2，王欣雅

（1.河南师范大学 计算机与信息工程学院，河南 新乡 453007；2.教育人工智能与个性化学习河南省重点实验室（河南师范大学），河南 新乡 453007）（∗通信作者电子邮箱sunlin@htu.edu.cn）

基于邻域粗糙集和帝王蝶优化的特征选择算法

孙林1，2*，赵婧1，徐久成1，2，王欣雅1

（1.河南师范大学 计算机与信息工程学院，河南 新乡 453007；2.教育人工智能与个性化学习河南省重点实验室（河南师范大学），河南 新乡 453007）（∗通信作者电子邮箱sunlin@htu.edu.cn）

针对经典的帝王蝶优化（MBO）算法不能很好地处理连续型数据，以及粗糙集模型对于大规模、高维复杂的数据处理能力不足等问题，提出了基于邻域粗糙集（NRS）和MBO的特征选择算法。首先，将局部扰动和群体划分策略与MBO算法结合，并构建传输机制以形成一种二进制MBO（BMBO）算法；其次，引入突变算子增强算法的探索能力，设计了基于突变算子的BMBO（BMBOM）算法；然后，基于NRS的邻域度构造适应度函数，并对初始化的特征子集的适应度值进行评估并排序；最后，使用BMBOM算法通过不断迭代搜索出最优特征子集，并设计了一种元启发式特征选择算法。在基准函数上评估BMBOM算法的优化性能，并在UCI数据集上评价所提出的特征选择算法的分类能力。实验结果表明，在5个基准函数上，BMBOM算法的最优值、最差值、平均值以及标准差明显优于MBO和粒子群优化（PSO）算法；在UCI数据集上，与基于粗糙集的优化特征选择算法、结合粗糙集与优化算法的特征选择算法、结合NRS与优化算法的特征选择算法、基于二进制灰狼优化的特征选择算法相比，所提特征选择算法在分类精度、所选特征数和适应度值这3个指标上表现良好，能够选择特征数少且分类精度高的最优特征子集。

帝王蝶优化；特征选择；邻域粗糙集；邻域依赖度；二进制

0 引言

特征选择是数据挖掘与机器学习领域中一个必不可少的数据预处理步骤［1-2］。特征选择一般分为启发式和穷举式搜索两种策略。当使用穷举式搜索对特征数非常大的数据集进行特征选择时，将所有特征子集列出是不现实的。为避免这一问题，许多研究者转向研究启发式搜索策略，如元启发式算法。当前，已经有许多学者结合元启发式算法解决特征选择优化问题，例如：Hu等［3］提出了一种二进制灰狼算法并应用于特征选择；Tubishat等［4］基于对立学习的樽海鞘群算法设计了一种局部搜索的特征选择算法。因而，元启发式特征选择是目前流行的数据分类策略。

粗糙集理论是特征选择的一种有效数学工具［5-6］。尽管粗糙集模型具有能够去除不相关、冗余的特征，并保留原始特征的特性，但也是一种NP-Hard问题，很难找到最优解，而这正好被元启发式算法弥补。Zaimoglu等［7］提出了基于粗糙集和拔河优化算法的特征选择策略；Huda等［8］构建了基于粒子群优化和粗糙集的特征选择算法；Tawhid等［9］提出了基于粗糙集和二进制鲸鱼优化的特征选择算法；Wang等［10］运用量子对蝗虫优化算法进行改进，设计了基于互信息和粗糙集的动态种群量子二进制蝗虫优化算法；Abd等［11］考虑到还原集中特征的数量和分类质量，将布谷鸟搜索结合粗糙集理论来构建适应度函数，提出了基于粗糙集的布谷鸟搜索算法。但是，上述基于粗糙集的特征选择算法仅适用于符号型数据，若需要处理连续型数据，则必须进行离散化处理，这将不可避免地丢失一些重要信息［12］。为了解决这个问题，研究人员对粗糙集理论进行扩展研究，提出了邻域粗糙集（Neighborhood Rough Set， NRS）模型、模糊粗糙集、公差近似模型等［13］。邻域粗糙集不仅可以处理连续型数据，而且也能处理符号型和数值型的混合数据［14］。Zou等［12］通过引入自适应函数来控制人工鱼的视觉和步长，结合鱼群算法和邻域粗糙集理论构建特征选择算法。基于邻域粗糙集的特征选择旨在从邻域决策系统中获取最优/最小的特征子集［15］。截至目前，将邻域粗糙集与群智能优化算法结合是数据挖掘领域中特征选择的最重要的研究方向之一。

群智能优化算法是受生物群体间的智能协作过程启发而设计的一类算法，具有实现容易、并行性好、连续和离散区间问题适应性强等优点，已经成为当前各类优化问题尤其是组合问题的求解方法［16］。受美国帝王蝶迁徙行为的启发，Wang等［17］提出了帝王蝶优化（Monarch Butterfly Optimization， MBO）算法。该算法模拟帝王蝶利用两个算子进行种群更新的行为，具有计算简单、参数较少、收敛迅速、易于程序实现等优点，于是该算法在许多领域得到了广泛的应用，例如：Dorgham等［18］采用MBO算法寻找最优阈值，使用质量结构相似指数矩阵评价分割后的图像精度，提高图像分割性能。Soltani等［19］开发了一种基于MBO算法高效的神经网络模拟系统。截止到目前，利用MBO算法解决特征选择优化问题的应用研究较少。孙林等［20］基于柯西变异的差分自适应MBO算法，结合K近邻分类器提出了特征选择算法。但是该算法仍存在一些问题：不能处理连续型数据，可搜索位置有限，容易陷入局部最优等。

为弥补这些局限性，利用邻域粗糙集模型既能分析连续型数据，又能处理符号与数值的混合型数据的优势，且二进制算子比连续算子具有更强的拟合性的特点，提出了基于邻域粗糙集和帝王蝶优化的特征选择算法。首先，为了使帝王蝶个体在寻找最优解时有更强的搜索能力，以避免过早陷入局部最优，在MBO算法上加入局部扰动，并结合群体划分策略，在到目前为止找到的最优解的位置生成了解的二进制形式，构造出二进制MBO（Binary MBO， BMBO）算法；且为了进一步增强BMBO算法的搜索能力，引入突变算子增强探测阶段，设计了基于突变算子的BMBO（BMBO based on Mutation operator， BMBOM）算法。然后，使用邻域粗糙集的邻域依赖度和所选特征子集的加权值构造新的适应度函数，对选出的特征子集进行评估并排序。最后，结合新的适应度函数，设计了基于邻域粗糙集与BMBOM的特征选择算法（Feature Selection algorithm based on Neighborhood rough set and BMBOM， FSNB），寻找最优特征子集使其在优化问题空间中具有更强的搜索能力，有效获取最优/最小特征子集。在6个基准函数和14个UCI数据集上的实验结果表明，本文算法能够选择分类精度较高且数量规模较小的特征子集。

1 基础知识

1.1 邻域粗糙集

1.2 帝王蝶优化算法

将帝王蝶优化（MBO）算法用于解决全局优化问题，性能优于其他先进的典型优化算法［17］。MBO算法搜索过程由两种机制主导：迁移算子和调整算子，具体流程如算法1所示。

算法1 MBO算法。

输入 初始化所有参数，适应度函数f（x），群体的规模N，空间维度D，最大迭代次数T；

输出 最优帝王蝶个体的位置及相应的适应度值。

1） While 不满足最大迭代或停止条件 do

2）计算适应度值并排序，找到最优帝王蝶位置和其对应的适应度值；

11） else

14） end if

15） end for

16） end for

21） else

27） end if

28） end if

29） end for

30） end for

31）将新生成的子种群合并为1个整体种群；

33） End while

2 本文特征选择算法

2.1 改进的MBO算法

一般来说，MBO算法能找到全局最优解，但在某些时候，它可能会陷入局部最优解。在调整算子中，每只帝王蝶的步长是由dx和a决定，通过Lévy飞行完全识别搜索过程，但不能根据实际搜索情况进行调节，当步长过大时，MBO算法无法获得最优解。为了使步长向着最好的帝王蝶去改变，尝试扩大步长参数a的调节范围，进行局部扰动，以帮助MBO算法跳出局部最优解。因此将步长参数a改进为：

其中：Smax表示帝王蝶的最大步长；t表示当前迭代次数；tmax表示最大迭代次数；m表示步长参数a的调整因子，随着迭代次数的改变而改变。

接下来，对帝王蝶群体实施群体划分策略。设当前的帝王蝶群体为N，利用适应度函数计算群体中各个帝王蝶的适应度值Fit，并得到N中最佳适应度值Fitbest和最差适应度值Fitworst。利用分别计算帝王蝶个体i和最优个体的适应度差值di，best以及和最差个体的适应度差值di，worst。若di，best和di，worst满足，则帝王蝶个体i被划分到精英子群中，并直接保留到下一次迭代中；否则被划分到普通子群中，继续迭代更新。

依据上述思路改进MBO算法，获取分类结果，然后构建传输机制获得二进制表示：

结合MBO算法和式（11），本文构建二进制MBO（BMBO）算法。为了使解决方案朝着目前为止最佳的解决方案演化，可以通过适当的突变率对普通子群中的帝王蝶个体进行局部搜索来进行突变，从而生成新的解决方案。为了避免过早收敛，可以使用具有适当突变率的突变算子来增强算法的多样性，其中突变率是控制突变算子的关键因素［21］。过高的突变率会增加在搜索空间中搜索更多区域的概率，从而阻止种群收敛到任何最优解；太小的突变率可能导致过早收敛，降低局部最优而不是全局最优。因而，使用的突变率r3表示为：

其中tmax表示最大迭代次数。根据迭代次数i，参数r3从0.9线性递减到0。于是，利用突变率r3代替式（11）中的r2，形成突变算子增强搜索能力，进而设计BMBOM算法。

2.2 适应度函数

在特征选择的过程中，让每个帝王蝶分头并行地寻找最优特征子集，结合邻域依赖度与特征子集长度的加权值，构造新的适应度函数，并将其作为启发式信息引导算法进行迭代寻优。由此，基于邻域依赖度的适应度函数描述如下。

其中：|B|为所选特征子集的长度；|C|为特征总个数；表示邻域依赖度；λ和μ分别表示分类质量和子集长度的重要程度，两个参数和的设置参照文献［3］。

2.3 算法描述

依据邻域粗糙集模型和MBO算法原理，用BMBOM算法选出特征子集，通过适应度函数评估特征子集的适应度值，排序选出最优特征子集，则特征选择算法的伪代码如算法2所示。

算法2 基于邻域粗糙集与BMBOM的特征选择算法（FSNB）。

输出 最优特征子集。

1） While 不满足最大迭代或停止条件 do

2） 根据式（13）计算适应度值并排序，找到最优的帝王蝶位置和其对应的适应度值；

11） else

14） end if

15） end for

16） end for

21） else

27） end if

28） end if

29） end for

30） end for

31） 将新生成的子种群合并为1个整体种群；

33） End while

35）计算所有特征在测试集上的分类精度；

36）输出最佳解决方案的位置（选中的最优特征子集）。

下面给出算法2的时间复杂度分析：假设帝王蝶群体规模为N、子群1为N1、子群2为1、最大迭代次数为T、空间维度为D。由文献［22］可知，计算正域和邻域依赖度的时间复杂度为。FSNB的复杂度由每次迭代循环确定，具体分析如下：步骤2）使用邻域依赖度计算适应度函数，其时间复杂度为；步骤3）～4）的时间复杂度都为O（N）；步骤5）～16）的时间复杂度为O（N1D）；步骤17）～30）的时间复杂度为；步骤31）～33）的时间复杂度为O（N）；步骤34）～36）的时间复杂度为常数项。因此，FSNB在最坏情况下的总时间复杂度为O（TN2）。

3 实验与结果分析

3.1 BMBOM算法性能分析

为验证BMBOM算法的优化性能，选取文献［20］中典型的6个基准函数（如表1所示），与MBO算法［17］、粒子群优化（Particle Swarm Optimization， PSO）算法［8］进行测试与比较。表1中，单峰函数主要测试算法的寻优精度；多峰函数具有多个局部最优点检验算法的全局搜索性能和避免局部收敛的能力。这些函数的理论最优值为0。为了确保实验的公平性，依据文献［20］，这3种算法在30维上设置相同的参数。同时，为防止产生随机的实验结果影响对算法的评估，这3种算法在6个基准函数上独立运行30次。表2给出了3种算法在6个基准函数上30维的最优值、最差值、平均值、标准差和运行时间的测试结果。从表2测试结果可以看出，在上，BMBOM算法的最优值、最差值、平均值以及标准差都优于MBO算法和PSO算法；尤其在f1和f5上，BMBOM算法的5项指标远领先于其他2种算法；在f6上，PSO算法在标准差上是最优的，BMBOM算法在f6的最优值、最差值和平均值都是最优的。从运行时间上来说，BMBOM算法次于其他2种对比算法，其原因是：BMBOM算法中的局部扰动、群体划分策略以及突变算子在提高了优化性能的同时增加了运行时间。因此，这3种算法在6个基准函数30维上的实验结果表明，BMBOM算法获得的优化能力和稳定性是相对优异的。实验环境设置为64位Window 7、Intel Core i5 2.2 GHz CPU、4 GB RAM和Matlab 2016b，且文中所有实验结果中的加粗都表示最佳值。

表1 六个基准函数信息Tab. 1 Information of six benchmark functions

表2 三种优化算法在6个基准函数30维上的实验结果Tab. 2 Experimental results of three optimization algorithms on 30-dimensions of six benchmark functions

3.2 FSNB性能分析

为验证FSNB的特征选择效果，选用14个UCI数据集［21］进行测试。表3给出了所选数据集的信息。FSNB的种群数设置为20，最大迭代次数设置为100，依据文献［3］，设置适应度函数中且。实验采用3类评价指标［21］：分类精度、所选特征数和适应度值。为了验证结果的最优性并确保比较算法的公平性，参照文献［21］使用K最近邻分类器（），将每个数据集分为训练集占80%和测试集占20%。为了避免算法的随机性，每种算法独立运行20次，因而统计测量是20次独立运行的总体能力和最终结果。

3.2.1 与基于粗糙集的优化特征选择算法的比较

为了验证算法的有效性，首先将所提的FSNB与5种基于粗糙集的优化特征选择算法进行比较，分别包括：ARRSFA（Attribute Reduction based on Rough Sets and the discrete Firefly Algorithm）［23］、PSORSFS（Feature Selection algorithm based on Rough Sets and Particle Swarm Optimization）［24］、FSARSR（Rough Set Reducts with Fish Swarm Algorithm）［25］、QCSIA_FS（Cooperative Swarm Intelligence Algorithm based on Quantum-inspired and rough sets for Feature Selection）［26］、DQBGOA_MR（Dynamic population Quantum Binary Grasshopper Optimization Algorithm based on Mutual information and Rough set）［10］。这些算法使用对应文献中的最佳实验参数，对比的实验数据与结果选自文献［10］。表4给出了FSNB与其他5种特征选择算法在10个UCI数据集上的分类精度的实验结果。从表4可以看出，在Vote数据集上，FSNB比最优的FSARSR略差1.3个百分点；在其他9个数据集上，FSNB的分类精度都是最优的，尤其是在Wine数据集上，FSNB的分类精度比其他5种算法远高出23.3～29.9个百分点。同时，FSNB在分类精度平均值上是最优的，提升了11.6～14.0个百分点。由此可以说明，FSNB能够获得最优的分类精度。

表5给出了FSNB与其他5种特征选择算法所选择的特征数的实验结果。在Spect、Tic-tac-toe和Vote这3个数据集上，FSNB比其他5种算法具有显著优势。在Lungcancer数据集上，FSNB获取的特征数略逊于DQBGOA_MR，但是结合表4的分类精度综合分析可知，FSNB的分类性能远优于DQBGOA_MR。同样的，在其余6个数据集上，尽管FSNB所选的特征数不如其他5种算法，但是它们之间的差值较小，同时FSNB获得了具有明显优势的分类精度。综合考虑表4～5的实验结果可知，FSNB的分类能力优于其他5种算法。

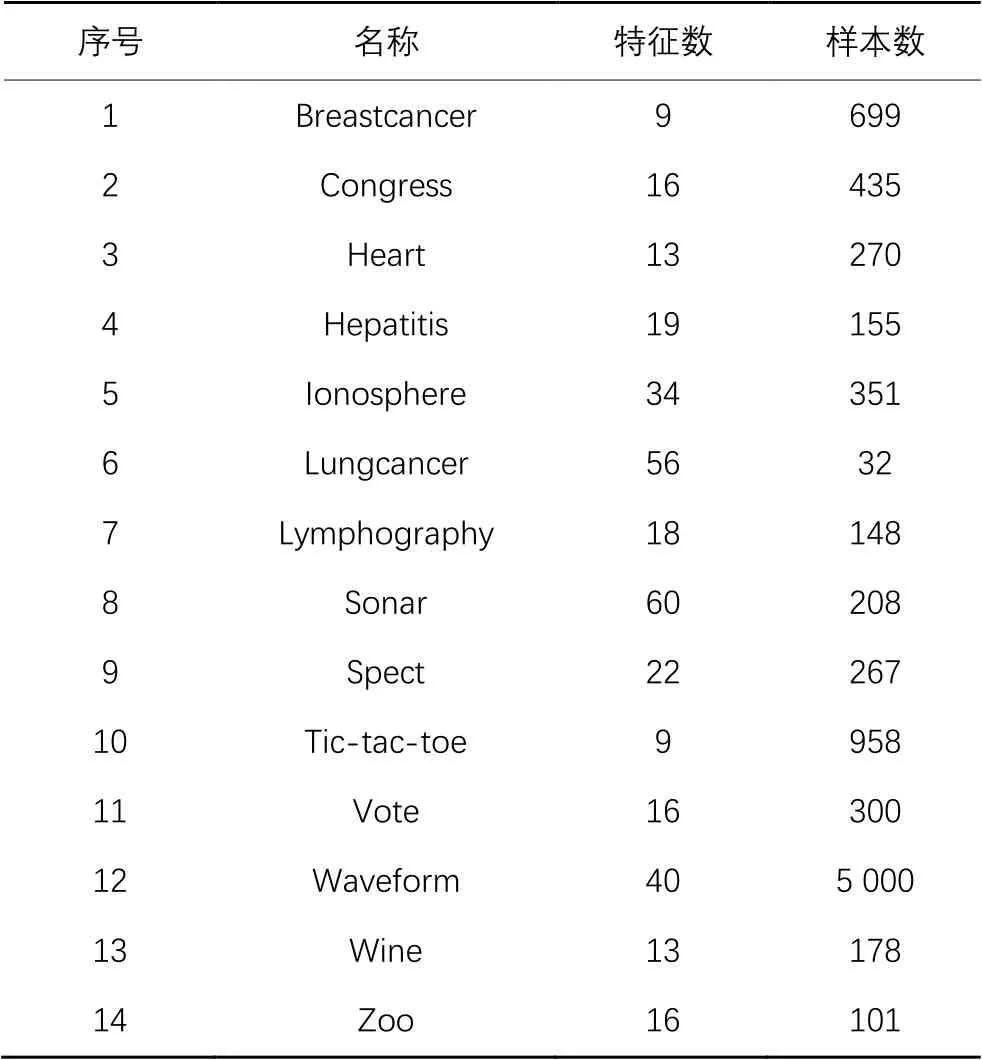
表3 14个UCI数据集信息Tab. 3 Information of fourteen UCI datasets

表4 FSNB与5种基于粗糙集的优化特征选择算法的分类精度实验结果 单位： %Tab. 4 Experimental results of FSNB and five optimized feature selection algorithms based on rough sets on classification accuracy unit： %

表5 FSNB与5种基于粗糙集的优化特征选择算法的所选特征数实验结果Tab. 5 Experimental results of FSNB and five optimized feature selection algorithms based on rough set on number of selected features

接下来，为了进一步评估FSNB的分类性能，选用当前流行的8种优化算法：IRRA（Improved Runner-Root Algorithm）［27］、GA（Genetic Algorithm）［28］、PSO（Particle Swarm Optimization）［29］、ABC（Artificial Bee Colony）［30］、FA（Firefly Algorithm）［31］、SSO（Social Spider Optimization）［32］、CS（Cuckoo Search）［33］和HS（Harmony Search algorithm）［34］，与粗糙集 （Rough Set）模型结合，构造8种特征选择算法进行对比，分别简写为IRRARS、GARS、PSORS、ABCRS、FARS、SSORS、CSRS和HSRS。上述8种优化算法使用对应文献中的最佳实验参数，对比的实验数据与结果选自文献［27］。表6给出了FSNB与上述8种特征选择算法在7个UCI数据集上的分类精度的实验结果。从表6的比较结果可知，在Breastcancer数据集上，FSNB的分类精度比IRRARS略低了2.3个百分点，但是优于GARS、PSORS、FARS、SSORS和CSRS这5种算法；在Lungcancer数据集上，FSNB的分类精度比其他8种算法高出了13.2～29.2个百分点；在Heart、Ionosphere、Waveform和Zoo这4个数据集上，FSNB也明显优于其他8种算法，同时也获得了相对最好的分类精度；而在Congress数据集上，FSNB的分类精度并没有其他8种算法好，但是在选择的特征数上来讲，FSNB占据了绝对的优势。尽管FSNB在Breastcancer和Congress数据集上的分类精度不是最优的，但相较于其余8种算法，FSNB还是具有较好的优势。同时，FSNB在分类精度平均值上是最高的，提升了3.9～13.2个百分点。表7中给出了FSNB和其他8种算法所选特征数。与这8种结合粗糙集的元启发式特征选择算法相比，FSNB在7个数据集上表现出了优越的性能，所选特征数远少于其他8种算法。详细来说，在Waveform数据集上，GARS所选特征数是FSNB的606倍；在Breastcancer和Congress这2个数据集上，FSNB虽然没有获得最高分类精度，但是选择的特征数取得了最小值，尤其是IRRARS和SSORS这2个算法选择的特征数分别是FSNB的57倍和30倍，表明FSNB的分类性能是最优的。

总的来说，从表4～7的实验结果可以看出，与粗糙集和优化算法结合的特征选择算法相比，FSNB在选择较少的特征的同时能够保持良好的分类精度。这表明FSNB选出的特征子集具有较少的数量和较高的分类精度，验证了FSNB的有效性。

表6 FSNB与8种结合粗糙集与优化算法的特征选择算法的分类精度实验结果 单位： %Tab. 6 Experimental results of FSNB and eight feature selection algorithms combining rough set and optimization algorithm on classification accuracy unit： %

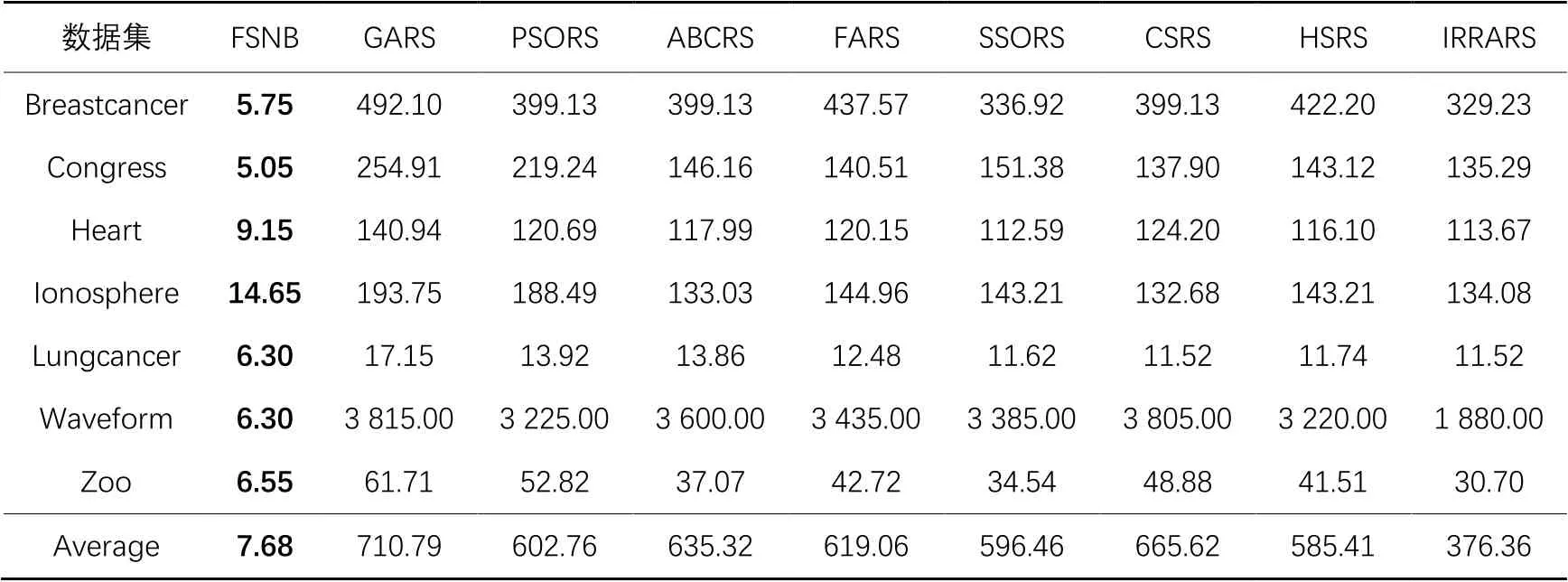
表7 FSNB与8种结合粗糙集与优化算法的特征选择算法所选特征数实验结果Tab. 7 Experimental results of FSNB and eight feature selection algorithms combining rough set and optimization algorithm on number of selected features

3.2.2 与基于邻域粗糙集的优化特征选择算法的比较

首先将邻域粗糙集与文献［17］的MBO算法相结合，构建新的特征选择算法FSNM（Feature Selection algorithm based on NRS and MBO），在选定的14个UCI数据集上，比较FSNM和FSNB的性能，验证BMBOM算法的优化性能。表8给出了3类指标的实验结果。

从表8可以看出，在14个UCI数据集上，FSNB获得了最优的分类精度和最少的特征数。详细来说，在Wine数据集上为最高分类精度97.53%；在Zoo、Waveform和Breastcancer这3个数据集上次之，分别为97.14%、96.89%和95.67%。在Congress和Heart这2个数据集上，FSNB的适应度值略低于FSNM，但是在分类精度和特征数上都优于FSNM。此外，在Waveform数据集上，FSNB选择的特征数最少，即为6.30。

同时，从表8可以看出，在Breastercancer、Hepatitis、Ionosphere等12个数据集上，FSNB获得了最优的适应度值，同时，在适应度值上，FSNB的平均值也是最优的。从运行时间上看出，在Breastcancer、Hepatitis、Ionosphere、Lungcancer、Lymphography、Waveform和Zoo这7个数据集上，FSNB优于FSNM，尤其是在Lymphography数据集上，FSNB的运行时间不到FSNM的6%；在Congress、Heart、Sonar和Wine这4个数据集上，FSNB与FSNM的运行时间是一样的；在Spect、Tic-tac-toe和Vote这3个数据集上，FSNB的运行时间次于FSNM；在平均值上，FSNB仍然优于FSNM。

从表8的4个评价指标总体结果来说，FSNB的分类结果优于FSNM。也就是说，BMBOM算法具有较好的优化分类性能。

接下来，为了验证FSNB的分类性能，选用当前流行的8种优化算法：IRRA［27］、GA［28］、PSO［29］、ABC［30］、FA［31］、SSO［32］、CS［33］和HS［34］，与邻域粗糙集模型结合构造8种特征选择算法进行对比，分别简写为IRRANRS、GANRS、PSONRS、ABCNRS、FANRS、SSONRS、CSNRS和HSNRS。对比的实验数据选自文献［27］。表9给出了FSNB与其他8种算法在分类精度上的实验比较结果。表10描述了FSNB与其他8种算法所选特征数的对比结果。

表8 FSNB与FSNM在分类精度、适应度值和所选特征数上的实验结果Tab. 8 Experimental results of FSNM and FSNB on classification accuracy， fitness value and number of selected features

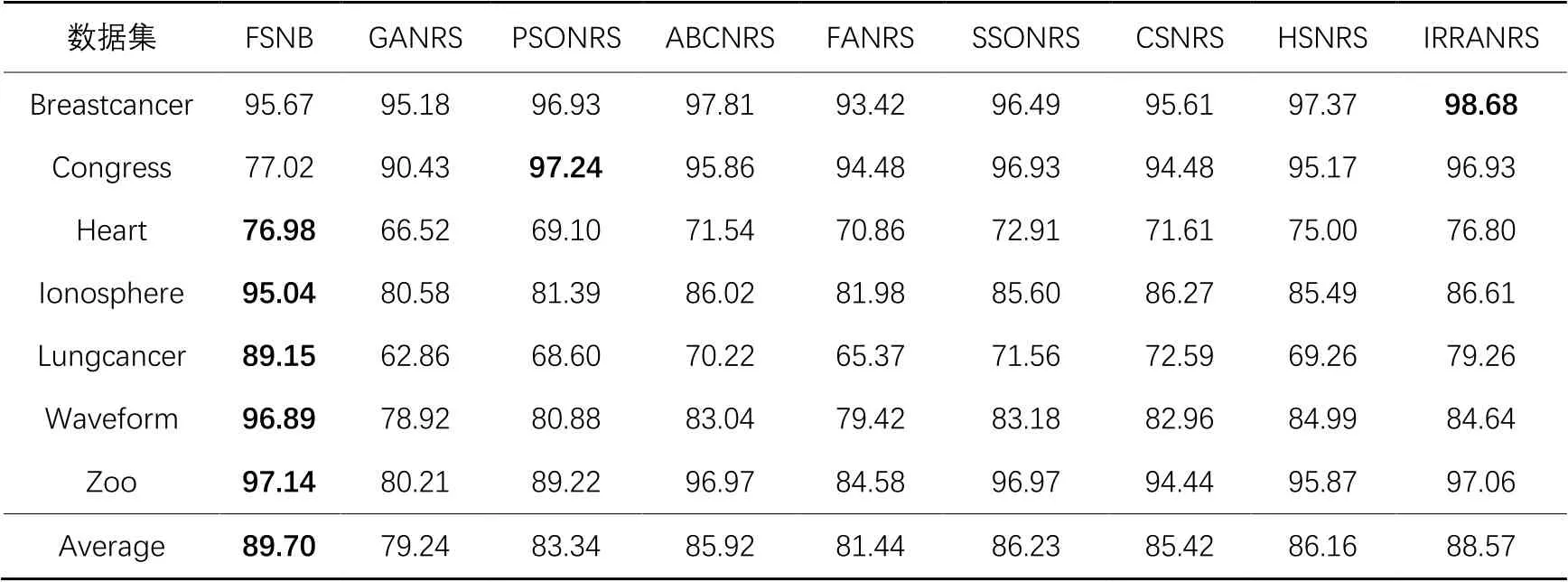
表9 FSNB与8种结合邻域粗糙集与优化算法的特征选择算法的分类精度实验结果 单位： %Tab. 9 Experimental results of FSNB and eight feature selection algorithms combining NRS and optimization algorithms on classification accuracy unit： %

表10 FSNB与8种结合邻域粗糙集与优化算法的特征选择算法所选特征数实验结果Tab. 10 Experimental results of FSNB and eight feature selection algorithms combining NRS and optimization algorithms on number of selected features

从表9可以看出，对于Heart、Ionosphere、Lungcancer、Waveform和Zoo这5个数据集，FSNB的性能最优。FSNB在除了Congress以外的6个数据集上都优于GANRS、FANRS和CSNRS这3个算法。值得一提的是，在Lungcancer数据集上，FSNB的分类精度明显优于其他8种算法。此外，在Zoo数据集上，FSNB的分类精度高达97.14%；而在Congress数据集上，FSNB的分类精度略低于其他8种算法，这可能是FSNB在迭代的过程中丢失了一些重要的特征，导致分类精度降低。

根据表10可知，在7个数据集上，FSNB选择的特征数依旧是最少的。尤其在Waveform数据集上，GANRS的特征数是FSNB的588倍。在Breastcancer和Congress这2个数据集上，FSNB虽然没有获得最高的分类精度，但是选择的特征数是最少的，并且IRRANRS和PSONRS这2个算法选择的特征数分别是FSNB的54倍和41倍。

总的来说，在Heart、Ionosphere、Lungcancer、Waveform和Zoo这5个数据集上，FSNB的分类精度是稳定的，而GANRS、ABCNRS、FANRS、CSNRS和HSNRS这5种算法的分类性能是不稳定的。同时，FSNB在分类精度和特征数上总的平均值都是最优的，即在分类精度平均值上提升了1.1～10.5个百分点，在所选特征数的平均值上比其他算法少了347～678。因此，FSNB能够有效消除冗余特征并显著提高算法的分类精度，优于其他8种算法，也就是说FSNB在解决特征选择问题上具有明显的优势。

3.2.3 与基于二进制灰狼优化的特征选择算法的比较

为了更好地展示FSNB的有效性，从文献［3］中选择6种基于二进制灰狼优化（Binary Grey Wolf Optimizer）的特征选择算法，具体包括：BGWO、ABGWO、ABGWO-V1、ABGWO-V2、ABGWO-V3和ABGWO-V4，与本文提出的FSNB进行实验比较。上述6种算法使用文献［3］中对应的最佳实验参数，对比的实验数据与结果也选自文献［3］。表11给出了FSNB与6种基于二进制灰狼优化的特征选择算法的分类精度比较结果。

从表11可以看出，在Congress数据集上，FSNB的分类精度略低于最优的ABGWO。但是，在其余8个数据集上，FSNB获得最优的分类精度，尤其是在Zoo数据集上的分类精度最高，即为97.14%；在Lymphography数据集上，FSNB的分类精度明显比其他6种算法高出44.1～45.4个百分点。同时，FSNB在分类精度的平均值上是最优的，即提升了13.5～14.3个百分点。

表12给出了FSNB与其他6种算法所选特征数比较结果。从表12可以看出，FSNB表现最优，其次是ABGWO-V2和ABGWO-V3这2种算法。在Congress、Sonar、Spect、Tic-tac-toe、Waveform和Zoo这6个数据集上，FSNB选取的特征数为最小值。在Breastcancer和Ionosphere这2个数据集上，虽然FSNB的特征数都不如ABGWO-V2算法，但FSNB的分类精度值分别比ABGWO-V2算法高出15.4个百分点和8.1个百分点；而在Lymphography数据集上，FSNB的特征数少于ABGWO-V3算法，但FSNB的分类精度是7种算法中最高的。总体来说，综合考虑分类精度和所选特征数这2个评价指标，FSNB明显优于这6种基于二进制灰狼优化的特征选择算法。

表11 FSNB与6种基于二进制灰狼优化的特征选择算法的分类精度实验结果 单位： %Tab. 11 Experimental results of FSNB and six feature selection algorithms based on binary grey wolf optimizer on classification accuracy unit： %

表12 FSNB与6种基于二进制灰狼优化的特征选择算法所选特征数实验结果Tab. 12 Experimental results of FSNB and six feature selection algorithms based on binary grey wolf optimizer on number of selected features

3.3 统计分析

使用Friedman和Bonferroni-Dunn测试［35］来分析所有实验结果的统计意义，计算式为：

其中：k是算法数量；N是数据集数量；Ri是k个算法在N个数据集上的平均排名。依据测试结果可知，如果平均距离水平超出临界距离，则算法性能有显著差异。临界距离定义为：

其中：qα是测试的关键列表值；α表示显著水平。

依据表5、7、9、11的分类精度实验结果，分别对所有比较的算法进行Friedman检验，验证所有算法在分类性能上是否存在显著性差异，表13～16分别给出了在KNN分类器下的排序结果和2个评价指标（和）的值。

为了直观地显示FSNB与其他对比算法的相对性能，图1给出了比较的算法在分类精度下的值，其中每个算法的平均排序沿数轴绘制。轴上的最小值位于左侧，因此，左侧排序的算法更好。表13给出了FSNB与5种基于粗糙集的优化特征选择算法的平均排序和值，其中，的零假设被拒绝。如图1所示，在显著性水平下，，，其中且，由此可知，FSNB明显优于其他5种算法。表14给出了FSNB与8种结合粗糙集与优化的特征选择算法的平均排序和值，其中的临界值为，时拒绝零假设。图2显示了在显著性水平下，，，其中且，由此可以看出，IRRARS结果最优，FSNB次之，但是FSNB优于其他7种算法。表15给出了FSNB与8种结合邻域粗糙集与优化的特征选择算法的平均排序和值，其中的临界值为1.802，时的零假设将被拒绝。如图3所示，在显著性水平下，，其中且。因而可知，IRRANRS最优，FSNB次之，但是FSNB优于其他7种算法。表16给出了FSNB与6种基于二进制灰狼优化的特征选择算法的平均排序以及值，其中的临界值为1.901，时的零假设被拒绝。图4显示了在时，，其中且。因此，FSNB的Bonferron-Dunn检验优于其他6种算法。

总的来说，通过上述统计结果的分析可知，FSNB的性能优于其他比较算法，并在所有数据集上实现了良好的泛化性能。

表13 FSNB与5种基于粗糙集的优化特征选择算法的统计检验Tab. 13 Statistical test of FSNB and five optimized feature selection algorithms based on rough set

表14 FSNB与8种结合粗糙集与优化算法的特征选择算法的统计检验Tab. 14 Statistical test of FSNB and eight feature selection algorithms combining rough set and optimization algorithms

表15 FSNB与8种结合邻域粗糙集与优化算法的特征选择算法的统计检验Tab. 15 Statistical test of FSNB and eight feature selection algorithms combining NRS and optimization algorithms

表16 FSNB与6种基于二进制灰狼优化的特征选择算法的统计检验Tab. 16 Statistical test of FSNB and six feature selection algorithms based on binary grey wolf optimizer

图1 FSNB与5种基于粗糙集的优化特征选择算法的Bonferroni-Dunn检验结果Fig. 1 Bonferroni-Dunn test results of FSNB and five optimized feature selection algorithms based on rough set

图2 FSNB与8种结合粗糙集与优化算法的特征选择算法的Bonferroni-Dunn检验结果Fig. 2 Bonferroni-Dunn test results of FSNB and eight feature selection algorithms based on rough set and optimization algorithms

图3 FSNB与8种结合邻域粗糙集与优化算法的特征选择算法的Bonferroni-Dunn检验结果Fig. 3 Bonferroni-Dunn test results of FSNB and eight feature selection algorithms based on NRS and optimization algorithms

图4 FSNB与6种基于二进制灰狼优化的特征选择算法的Bonferroni-Dunn检验结果Fig. 4 Bonferroni-Dunn test results of FSNB and six feature selection algorithms based on binary grey wolf optimizer

4 结语

本文利用MBO算法的计算简单、所需计算参数较少、收敛迅速等优点，提出了一种基于邻域粗糙集与改进的MBO的特征选择算法。首先，针对获取的数据构建邻域决策系统，设计了BMBOM算法；然后，基于邻域粗糙集构造适应度函数，评估初始化的特征子集的适应度值并排序；最后，使用BMBOM算法搜索最优特征子集，设计了一种元启发式的特征选择算法。在6个基准函数和14个UCI数据集上的实验结果表明，所提算法是有效的。究其原因是在MBO算法上加入了局部扰动和群体划分策略，促使MBO算法能够最大化地搜索特征空间达到最优，加入突变算子使改进的MBO算法的多样性增强，进而更容易收敛到最优/接近最优解。将邻域粗糙集模型与改进的MBO算法相结合，使该特征选择算法更快地找到最小特征子集，特别是在处理高维数据时效果更加明显。但是，在算法运行时效上，本文所提算法的改善效果不够显著，在下一步研究工作中需继续改进。

[1] 吴信东，董丙冰，堵新政，等.数据治理技术［J］.软件学报，2019，30（9）：2830-2856.（WU X D， DONG B B， DU X Z， et al. Data governance technology ［J］. Journal of Software， 2019， 30（9）： 2830-2856.）

[2] 邓威，郭钇秀，李勇，等.基于特征选择和Stacking集成学习的配电网网损预测［J］.电力系统保护与控制，2020，48（15）：108-115.（DENG W， GUO Y X， LI Y， et al. Power losses prediction based on feature selection and Stacking integrated learning ［J］. Power System Protection and Control， 2020， 48（15）： 108-115.）

[3] HU P， PAN J S， CHU S C. Improved binary grey wolf optimizer and its application for feature selection ［J］. Knowledge-Based Systems， 2020，195： Article No.105746.

[4] TUBISHAT M， IDRIS N， SHUIB L， et al. Improved salp swarm algorithm based on opposition based learning and novel local search algorithm for feature selection ［J］. Expert Systems with Applications， 2020， 145： Article No.113122.

[5] 刘艳，程璐，孙林.基于K-S检验和邻域粗糙集的特征选择方法［J］.河南师范大学学报（自然科学版），2019，47（2）：21-28.（LIU Y， CHENG L， SUN L. Feature selection method based on K-S test and neighborhood rough sets ［J］. Journal of Henan Normal University （Natural Science Edition）， 2019， 47（2）： 21-28.）

[6] 刘琨，封硕.加强局部搜索能力的人工蜂群算法［J］.河南师范大学学报（自然科学版），2021，49（2）：15-24.（LIU K， FENG S. An improved artificial bee colony algorithm for enhancing local search ability ［J］. Journal of Henan Normal University （Natural Science Edition）， 2021， 49（2）： 15-24.）

[7] ZAIMOGLU E A， CELEBI N， YURTAY N. Binary-coded tug of war optimization algorithm for attribute reduction based on rough set ［J］. Journal of Multiple-Valued Logic and Soft Computing， 2020， 35（1/2）： 93-111.

[8] HUDA R K， BANKA H. Efficient feature selection and classification algorithm based on PSO and rough sets ［J］. Neural Computing and Applications， 2019， 31（8）： 4287-4303.

[9] TAWHID M A， IBRAHIM A M. Feature selection based on rough set approach， wrapper approach， and binary whale optimization algorithm ［J］. International Journal of Machine Learning and Cybernetics， 2020， 11（3）： 573-602.

[10] WANG D， CHEN H M， LI T R， et al. A novel quantum grasshopper optimization algorithm for feature selection ［J］. International Journal of Approximate Reasoning， 2020， 127： 33-53.

[11] ABD EL AZIZ M， HASSANIEN A E. Modified cuckoo search algorithm with rough sets for feature selection ［J］. Neural Computing and Applications， 2018， 29（4）： 925-934.

[12] ZOU L， LI H X， JIANG W， et al. An improved fish swarm algorithm for neighborhood rough set reduction and its application ［J］. IEEE Access，2019， 7： 90277-90288.

[13] 薛占熬，庞文莉，姚守倩，等.基于前景理论的直觉模糊三支决策模型［J］.河南师范大学学报（自然科学版），2020，48（5）：31-36，79.（XUE Z A， PANG W L， YAO S Q， et al. The prospect theory based intuitionistic fuzzy three-way decisions model ［J］. Journal of Henan Normal University （Natural Science Edition）， 2020， 48（5）： 31-36， 79.）

[14] HU Q H， YU D R， LIU J F， et al. Neighborhood rough set based heterogeneous feature subset selection ［J］. Information Sciences， 2018， 178（18）： 3577-3594.

[15] 彭鹏，倪志伟，朱旭辉，等.基于改进二元萤火虫群优化算法和邻域粗糙集的属性约简方法［J］.模式识别与人工智能，2020，33（2）：95-105.（PENG P， NI Z W， ZHU X H， et al. Attribute reduction method based on improved binary glowworm swarm optimization algorithm and neighborhood rough set ［J］. Pattern Recognition and Artificial Intelligence， 2020， 33（2）： 95-105.）

[16] SUN L， CHEN S S， XU J C， et al. Improved monarch butterfly optimization algorithm based on opposition-based learning and random local perturbation ［J］. Complexity， 2019， 2019： Article No.4182148.

[17] WANG G G， DEB S， CUI Z H. Monarch butterfly optimization ［J］. Neural Computing and Applications， 2019， 31（7）： 1995-2014.

[18] DORGHAM O M， ALWESHAH M， RYALAT M H， et al. Monarch butterfly optimization algorithm for computed tomography image segmentation ［J］. Multimedia Tools and Applications， 2021， 80（20）： 30057-30090.

[19] SOLTANI P， HADAVANDI E. A monarch butterfly optimization- based neural network simulator for prediction of siro-spun yarn tenacity ［J］. Soft Computing， 2019， 23（20）： 10521-10535.

[20] 孙林，赵婧，徐久成，等.基于改进帝王蝶优化算法的特征选择方法［J］.模式识别与人工智能，2020，33（11）：981-994.（SUN L， ZHAO J， XU J C， et al. Feature selection method based on improved monarch butterfly optimization algorithm ［J］. Pattern Recognition and Artificial Intelligence， 2020， 33（11）： 981-994.）

[21] MAFARJA M， ALJARAH I， FARIS H， et al. Binary grasshopper optimisation algorithm approaches for feature selection problems ［J］. Expert Systems with Applications， 2019， 117： 267-286.

[22] SUN L， WANG L Y， DING W P， et al. Feature selection using fuzzy neighborhood entropy-based uncertainty measures for fuzzy neighborhood multigranulation rough sets ［J］. IEEE Transactions on Fuzzy Systems， 2021， 29（1）： 19-33.

[23] LONG N C， MEESAD P， UNGER H. Attribute reduction based on rough sets and the discrete firefly algorithm ［M］// BOONKRONG S， UNGER H， MEESAD P. Recent Advances in Information and Communication Technology，AISC 265. Cham： Springer， 2014： 13-22.

[24] WANG X Y， YANG J， TENG X L， et al. Feature selection based on rough sets and particle swarm optimization ［J］. Pattern Recognition Letters， 2007， 28（4）： 459-471.

[25] CHEN Y M， ZHU Q X， XU H R. Finding rough set reducts with fish swarm algorithm ［J］. Knowledge-Based Systems， 2015， 81： 22-29.

[26] ZOUACHE D， BEN ABDELAZIZ F. A cooperative swarm intelligence algorithm based on quantum-inspired and rough sets for feature selection ［J］. Computers and Industrial Engineering， 2018， 115： 26-36.

[27] IBRAHIM R A， ABD ELAZIZ M， OLIVA D， et al. An improved runner-root algorithm for solving feature selection problems based on rough sets and neighborhood rough sets ［J］. Applied Soft Computing， 2020，97（Pt B）： Article No.105517.

[28] JING S Y. A hybrid genetic algorithm for feature subset selection in rough set theory ［J］. Soft Computing， 2014， 18（7）： 1373-1382.

[29] ZHANG Y， GONG D W， HU Y， et al. Feature selection algorithm based on bare bones particle swarm optimization ［J］. Neurocomputing， 2015， 148： 150-157.

[30] SUGUNA N， THANUSHKODI K G. An independent rough set approach hybrid with artificial bee colony algorithm for dimensionality reduction ［J］. American Journal of Applied Sciences， 2011， 8（3）： 261- 266.

[31] 汪春峰，褚新月.基于精英邻居引导的萤火虫算法［J］.河南师范大学学报（自然科学版），2019，47（6）：15-21.（WAND C F， CHU X Y. A firefly algorithm based on elite neighborhood guide ［J］. Journal of Henan Normal University （Natural Science Edition）， 2019， 47（6）： 15-21.）

[32] ABD EL AZIZ M， HASSANIEN A E. An improved social spider optimization algorithm based on rough sets for solving minimum number attribute reduction problem ［J］. Neural Computing and Applications， 2018， 30（8）： 2441-2452.

[33] 徐小琴，王博，赵红生，等.基于布谷鸟搜索和模拟退火算法的两电压等级配网重构方法［J］.电力系统保护与控制，2020，48（11）：84-91.（XU X Q， WANG B， ZHAO H S， et al. Reconfiguration of two-voltage distribution network based on cuckoo search and simulated annealing algorithm ［J］. Power System Protection and Control， 2020， 48（15）： 108-115.）

[34] INBARANI H H， BAGYAMATHI M， AZAR A T. A novel hybrid feature selection method based on rough set and improved harmony search ［J］. Neural Computing and Applications， 2015， 26（8）： 1859-1880.

[35] SUN L， WANG L Y， DING W P， et al. Neighborhood multi- granulation rough sets-based attribute reduction using Lebesgue and entropy measures in incomplete neighborhood decision systems ［J］. Knowledge-Based Systems， 2020， 192： Article No.105373.

Feature selection algorithm based on neighborhood rough set and monarch butterfly optimization

SUN Lin1，2*， ZHAO Jing1， XU Jiucheng1，2， WANG Xinya1

（1.College of Computer and Information Engineering，Henan Normal University，Xinxiang Henan453007，China；2.Key Laboratory of Artificial Intelligence and Personalized Learning in Education of Henan Province（Henan Normal University），Xinxiang Henan453007，China）

The classical Monarch Butterfly Optimization （MBO） algorithm cannot handle continuous data well， and the rough set model cannot sufficiently process large-scale，high-dimensional and complex data. To address these problems， a new feature selection algorithm based on Neighborhood Rough Set （NRS） and MBO was proposed. Firstly， local disturbance， group division strategy and MBO algorithm were combined， and a transmission mechanism was constructed to form a Binary MBO （BMBO） algorithm. Secondly， the mutation operator was introduced to enhance the exploration ability of this algorithm， and a BMBO based on Mutation operator （BMBOM） algorithm was proposed. Then， a fitness function was developed based on the neighborhood dependence degree in NRS， and the fitness values of the initialized feature subsets were evaluated and sorted. Finally， the BMBOM algorithm was used to search the optimal feature subset through continuous iterations， and a meta-heuristic feature selection algorithm was designed. The optimization performance of the BMBOM algorithm was evaluated on benchmark functions， and the classification performance of the proposed feature selection algorithm was evaluated on UCI datasets. Experimental results show that， the proposed BMBOM algorithm is significantly better than MBO and Particle Swarm Optimization （PSO） algorithms in terms of the optimal value， worst value， average value and standard deviation on five benchmark functions. Compared with the optimized feature selection algorithms based on rough set， the feature selection algorithms combining rough set and optimization algorithms， the feature selection algorithms combining NRS and optimization algorithms，the feature selection algorithms based on binary grey wolf optimization， the proposed feature selection algorithm performs well in the three indicators of classification accuracy， the number of selected features and fitness value on UCI datasets，and can select the optimal feature subset with few features and high classification accuracy.

Monarch Butterfly Optimization (MBO); feature selection; Neighborhood Rough Set (NRS); neighborhood dependence degree; binary

TP181

A

1001-9081（2022）05-1355-12

10.11772/j.issn.1001-9081.2021030497

2021⁃04⁃02；

2021⁃09⁃15；

2021⁃09⁃22。

国家自然科学基金资助项目（62076089，61772176，61976082）；河南省科技攻关项目（212102210136）。

孙林（1979—），男，河南南阳人，副教授，博士，CCF会员，主要研究方向：粒计算、数据挖掘、机器学习、生物信息学； 赵婧（1996—），女，河南洛阳人，硕士研究生，主要研究方向：数据挖掘、机器学习； 徐久成（1963—），男，河南洛阳人，教授，博士生导师，博士，CCF高级会员，主要研究方向：粒计算、数据挖掘、机器学习； 王欣雅（1997—），女，河南平顶山人，硕士研究生，主要研究方向：数据挖掘、机器学习。

This work is partially supported by National Natural Science Foundation of China （62076089， 61772176，61976082）， Key Scientific and Technological Project of Henan Province （212102210136）.

SUN Lin， born in 1979， Ph. D.， associate professor. His research interests include granular computing， data mining， machine learning， bioinformatics.

ZHAO Jing， born in 1996， M. S. candidate. Her research interests include data mining， machine learning.

XU Jiucheng， born in 1963， Ph. D.， professor. His research interests include granular computing， data mining， machine learning.

WANG Xinya， born in 1997， M. S. candidate. Her research interests include data mining， machine learning.