基于磁热双向耦合的永磁电机损耗和温升分析

孙若兰，彭辉灯，杨 都，杨光力，江晓波

(1.贵州航天林泉电机有限公司 国家精密微特电机工程技术研究中心，贵阳 550008；2.空装成都局驻贵阳地区第一军代表室，贵阳 550008)

0 引 言

高速永磁同步电机具有功率密度高、转矩密度高、效率高、可直接连接高速负载等优点，因此广泛应用于电动汽车、高速电主轴、航空航天等领域[1]。然而，转子的高损耗密度和较差的散热能力可能导致永磁体温升过高发生不可逆退磁，这被认为是高速永磁同步电机安全设计的关键之一。因此，准确的损耗和温升计算对于高速永磁同步电机至关重要。目前，较为常见的电机温升计算方法主要有两种：一是通过加载电机各部件的损耗密度法采用等效热网络法或有限元法来计算[2]；二是通过电磁场-温度场单向耦合仿真计算模型来计算[3-4]。其中方法一未能考虑电机各部件实际的损耗分布，方法二考虑了电机各部件实际的损耗分布，但两种方法均未能考虑温度对电机材料特性的影响。

一些研究人员采用单向耦合方法(OWCM)来解决文献[5-7]中的电磁-热耦合问题。在文献[5]中提出了一种感应电机的耦合磁热分析，其主要目标是实现对电机性能的快速和准确的预测。文献[7]侧重于将有限元法与集总参数热网络(LPTN)方法相结合以节省计算成本。为了考虑双向耦合效应，文献[8-13]中采用双向耦合方法(BDCM)来解决电磁-热耦合问题，以考虑温度对永磁体剩磁和矫顽力的影响。文献[13]中提出了一种基于磁-热-流体耦合迭代解的多物理场模拟，建立了电磁模型来解决电磁损耗，并使用CFD软件模拟对流条件。这两个结果都应用于电机的热分析。数据交互是双向的，以场的形式传递，充分考虑了电磁模型、CFD模型和热分析之间的相互作用，保证了计算结果的高精度。然而，忽略了温度对永磁体电导率的影响，存在高温状态下永磁体损耗计算误差大的问题。在文献[9-11]中，永磁体损耗仅通过二维有限元法计算而忽略了其端部效应，但实际上永磁体中的损耗分布不仅是径向的，还是轴向的。文献[8-13]中也没有考虑到温度对永磁体电导率的影响。

本文提出的方法在高速永磁同步电机的损耗和温升计算中综合考虑了温度对永磁体和绕组的电特性和磁特性的详细影响，提高了电机损耗和温升计算结果的准确性。电机的电磁损耗通过3-D瞬态有限元法计算，并根据实际损耗分布将损耗加载到3-D热模型中。本文结构如下，第二节给出了样机的主要参数和磁热双向耦合计算流程。在第三节中，讨论了温度对永磁体和绕组特性的详细影响分析。在额定负载正弦波供电及变频器供电条件下，采用有限元法计算了不同耦合方式的电机损耗和温升。在第四节中，给出了样机损耗和温升测试结果，以验证本文提出的磁-热双向耦合计算方法的准确性。最后得出结论，以证明所提出的磁-热双向耦合计算方法的必要应用范围。

1 电机的磁-热双向耦合计算模型

本节以一台15 kW，20000 r/min高速永磁电机为例，样机相关参数如表1所示，样机三维模型以及转子结构如图1所示。

图1 样机三维模型

2 磁热双向耦合计算模型

永磁同步电机在三维旋转电磁场中的数学计算模型为[14-15]

(1)

式中，A为矢量磁位，A=[Ax,Ay,Az]T，J为电流密度，J=[Jx,Jy,Jz]T，μ为介质的磁导率，S为第一类边界条件。

根据普通的热交换定律，当不考虑导热系数随电机不同位置变化，以及不考虑材料导热系数随温度变化时，温度场控制方程可表示为[16]

(2)

式中，λx、λy和λz为x、y和z方向的导热系数，qv为热源体密度，T0为S1边界上的温度，q0为边界面S2上的热流密度函数，αf为边界面S3的散热系数，Tf为边界面周围流体的温度。

由永磁同步电机电磁场和温度场的数学模型(1)(2)，可建立电机磁热双向耦合计算数学模型：

(3)

式中，GA为电磁场控制方程，t为温度，t′为GA中与温度有关的项，GT为温度控制方程，A′为温度场控制方程中与A有关的项。

为了实现电机电磁场与温度场之间的数据传递及迭代计算，采用了Ansys软件中的热模块，三维电磁场模块以及迭代模块。磁-热双向耦合计算流程示意图如图2所示。详细的流程如下：

(1)建立永磁同步电机的3-D模型，如图1所示。为确保在电磁场中求解的损耗数据完全传递到温度场中，相同的电机3-D模型用于电磁场和温度场计算。

(2)在电磁场中假设绕组和永磁体的工作温度，并设定绕组和永磁体的温度系数。

(3)将不同供电方式下电机的实测电流波形导入电磁场，计算出铜耗，定子铁心损耗，转子铁心损耗，永磁体涡流损耗。

(4)将流程(3)中计算得到的电机各部件损耗的结果传给预设的温度场计算模块，求解出电机的第一次温度场分布结果。

(5)通过设置迭代模块的迭代步数10以及前后两次温度计算结果误差小于1%，将温度场计算结果反馈到电磁场。

(6)通过(5)的迭代循环计算，在每个计算步骤中，绕组和永磁体的材料特性都会随温度发生变化，包括永磁体剩磁Br、矫顽力Hc和电导率σm，它们将反馈到电磁场进行计算，直到温度误差小于0.01，说明磁-热双向耦合计算完成。

图2 磁热双向耦合仿真流程图

3 永磁电机损耗和温升计算与分析

3.1 温度对永磁体材料属性的影响

永磁体的磁性能对电机的电磁性能有很大的影响，永磁体磁性能的变化直接影响到电磁功率损耗，尤其是电机的铁耗。在NdFeB永磁体的 B-H 曲线的线性部分，剩磁Br和矫顽力Hc随温度线性变化，可表示为[17]

(4)

(5)

式中，Br0和Hc0为环境温度T0时的剩磁密度和计算矫顽力，αBr和αHcj为Br和Hc的可逆温度系数(%/℃)，IL为Br的不可逆损失率，TPM为永磁体的工作温度(℃)。

永磁体的主要热源是涡流损耗，电导率对永磁体的涡流损耗影响很大。温度对电导率的影响可以表示为[18]

(6)

式中，c和d是常数;TPM为永磁体的工作温度，单位℃。

3.2 温度对铜材料属性的影响

温度对绕组电阻的影响很大，直接影响绕组的铜耗。温度变化对绕组电阻的影响如下：

ρcopper=ρ0(1+α(T-T0))

(7)

式中，ρcopper和ρ0分别为环境温度T0和工作温度T(℃)时的铜电阻率，α为铜电阻率的温度系数。

3.3 非晶合金铁心材料特性测试

定子铁心采用0.025 mm厚的非晶合金材料2605SA1制成。为了获得非晶合金铁心的电磁特性和损耗特性，基于德国BROCKHAUS软磁材料磁性能测量平台，按照国际标准对IEC 60404-2进行了测试。非晶合金铁心的磁化强度和损耗密度测试结果如图3和图4所示，可以看出不同频率下非晶合金铁心的磁化曲线基本相同。即材料的磁化曲线不会随着频率的变化而发生很大的变化。带材加工成铁心的过程中，饱和磁密度发生了变化，约为1.40T，小于非晶合金带材厂家提供的1.56T。

图3 不同频率下非晶合金实测B-H曲线

图4 不同频率下非晶合金实测损耗曲线

单位重量的铁损可以根据Bertotti[19]的损耗分离模型计算：

PBertotti=khystBβhystf+keddyB2f2+kexcessB1.5f1.5

(8)

式中，khyst，βhyst，keddy以及kexcess分别为磁滞损耗系数，涡流损耗系数以及附加损耗系数，f为频率，B为磁密幅值。

损耗系数可以通过将铁耗公式对图5中所示的测量损耗特性曲线进行拟合确定。非晶合金铁心损耗系数拟合结果如表2所示。

表2 非晶合金铁心损耗系数

3.4 单向耦合计算结果与双向耦合计算结果对比

为了研究温度对电机材料特性以及电机损耗分布特性的影响，将在三维电磁场中导入电机额定负载下的变频器供电实验电流波形，如图5(a)所示，图5(b)为电流波形的谐波频谱。

图5 额定负载下的变频器供电实验电流波形

在本节中，分别通过两种不同方法(分别是单向耦合和双向耦合)计算和分析了电机在正弦波供电及变频器供电条件下的损耗和温升。两种方法得到的电机损耗对比结果如表3所示。可以看出，样机变频器供电下，在考虑绕组和永磁体的温度特性后(双向耦合法)，铁心损耗的平均值为202.09 W，比未考虑绕组和永磁体的温度特性(单向耦合法)得到的结果减少了了9.4%。同样地，在未考虑温度对绕组和永磁体材料的影响情况下(磁热单向耦合法)，计算得到的绕组铜耗与永磁体涡流损耗结果分别为111.63 W，52.37 W；在考虑了温度对绕组和永磁体材料的影响之后(磁热双向耦合法)，计算得到的绕组铜耗与永磁体涡流损耗结果分别为137.35 W，73.17 W，比前者分别增大了18.7%，39.7%。

与正弦波供电相比，采用变频器供电时，电机的额定负载损耗增加了42.4%。这部分增量主要是由于变频器供电电流波形中含有大量时间谐波，引入了电机的谐波损耗。双向耦合法计算得到的正弦波供电及变频器供电条件下的永磁体涡流损耗密度分布如图6所示。可以看出，电机在变频器供电情况下的永磁体的涡流损耗明显高于在正弦波供电情况下的永磁体的涡流损耗。

表3 电机损耗计算结果对比

图6 同一时刻下永磁体涡流损耗密度分布

为了提高计算效率，采用1/2电机模型，如图1(a)所示。对电机计算模型进行了如下假设：

(1)电机温度沿圆周对称分布。

(2)绕组设定为内部实心铜，槽内的所有绝缘都相当于一个绝缘体。

(3)本文采用等效传导传热系数αeff来描述转子和定子之间的热交换能力，αeff的值取决于气隙的雷诺数。具体公式如下：

(9)

式中，λair为空气的导热系数，ro为转子外径，ri为定子内径，Reeff和Recr分别为气隙的雷诺数和临界雷诺数，计算公式如下：

(10)

(11)

式中，δ为气隙长度，vair为空气的动态粘度，μr为转子表面线速度。

(4)水道壁的对流换热系数可计算如下：

αw=Nuλ/De

(12)

式中，Nu为Nusselt准则，λ为水的导热系数，De为水的等效直径。

(5)铁心端面的散热系数可计算如下[20]：

αr=16.50.65μr0.65

(13)

(6)机壳表面的对流传热系数可由下式求得：

(14)

式中，β为机壳表面的温度。

(7)机壳的对流散热系数为14.2 W/(m2·K)。环境温度为20 ℃。

(8)电机各部件材料的导热系数如表4所示。

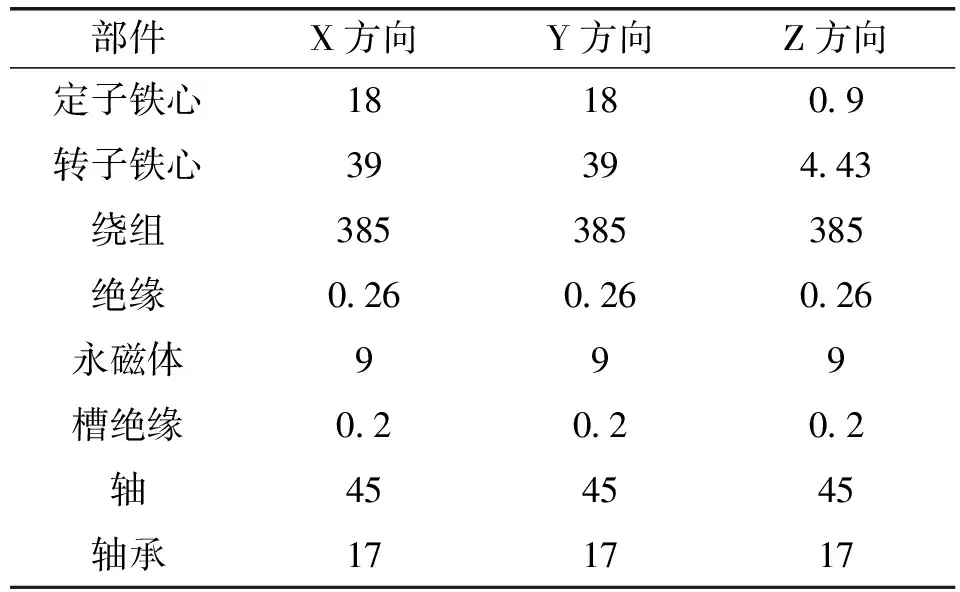
表4 电机材料导热系数 (单位：W/m-1K-1)

考虑到电机装配间隙，导热系数略有不同，电机不同部件的装配间隙如表5所示。装配间隙的导热系数为 0.0242 W/m-1K-1。

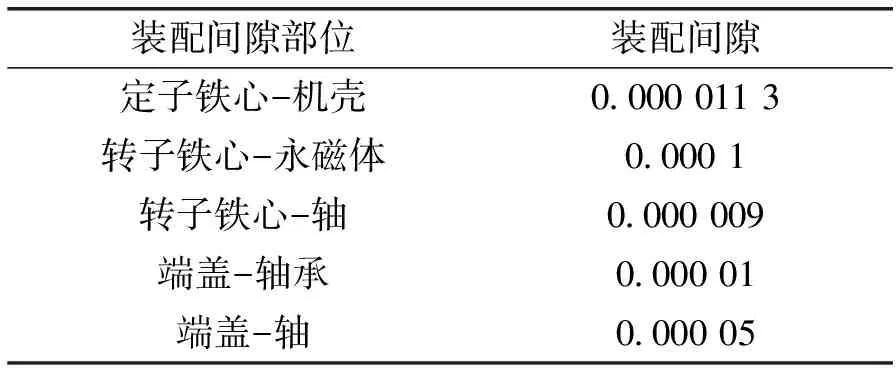
表5 电机各部件装配间隙 (单位：mm)

通过双向耦合法计算得到的电机在额定转速，不同供电方式下的温度场分布计算如图7所示。可以看出电机在正弦波供电下，最大温升在绕组处为61.6 K；电机在变频器供电下，最大温升在永磁体中部处为88.2 K。这是因为电机采用变频器供电时会引入大量的高次时间谐波电流，与电机内部空间谐波共同作用，在气隙内形成高频谐波磁场，产生的电流谐波磁动势使得电机永磁体涡流损耗显著高于正弦波供电下的永磁体涡流损耗。

图7 不同供电方式下电机的温度场分布

以变频器供电为例，对电机在3种不同计算方法下的温度场进行了计算和分析。这3种方法是：

方法A：采用传统的加载均匀损耗密度的方法。

方法B：采用单向耦合法并考虑电机装配间隙。

方法C：采用双向耦合法并考虑电机装配间隙。

电机在不同计算方法下温度计算结果如表6所示。电机中永磁体的温度分布如图8所示，方法C计算得到的电机最大温升为88.2K，比方法B得到的温升增加了5.2%。

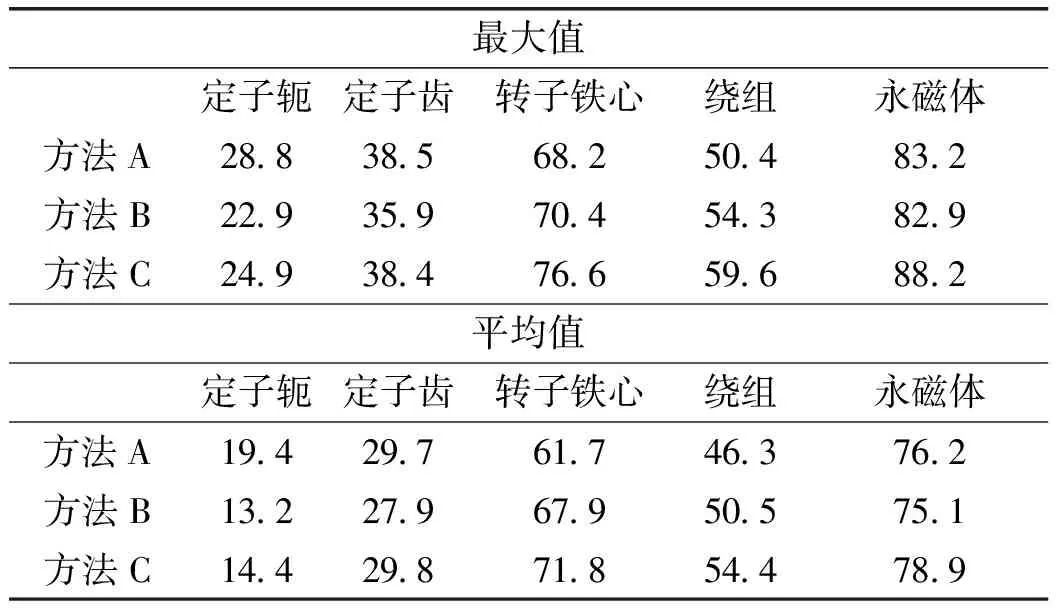
表6 电机温升计算结果 (单位：K)

图8 永磁体温度场分布(单位：℃)

方法C(双向耦合法)分析的收敛过程如图9所示，计算过程中永磁体参数及绕组参数的迭代结果如表6所示，其中方法B计算的损耗和温升结果对应迭代步数为零时的结果，方法C得到的结果对应迭代步数为4时的结果。

图9 磁热双向耦合分析的迭代收敛过程

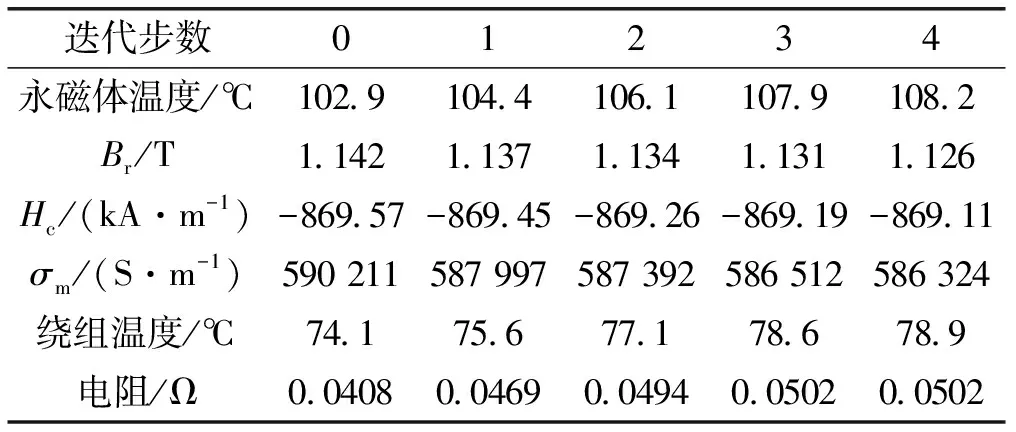
表7 磁热双向耦合法迭代结果

4 试验验证

4.1 额定负载损耗测试及分析

为了验证前文分析计算结果的准确性，采用两台样机进行对拖实验，对变频器供电下的高速永磁同步电机的额定负载损耗进行测试，试验布局如图10所示。两台完全相同的样机，一个用作电动机，另一个用作发电机。发电机的负载是一个电阻箱，可通过调整电阻箱的电阻来加载。样机的额定负载损耗可表示为

∑P=(Pin-Pout)/2

(15)

式中，Pin为电动机的输入功率，Pout为发电机的输出功率。

机械损耗Pmech可分为空气摩擦损耗Pair和轴承摩擦损耗Pbearing两部分。空气摩擦损失Pair可以通过下式获得[21]：

Pair=kCfπρairω3R4L

(16)

式中，k为粗糙度系数，ρair为空气的密度，ω为转子的角速度，R为转子的外径，L为转子的长度。Cf为摩擦系数。

轴承损耗可以通过文献[22]提出的经验方法从轴承摩擦扭矩估算出来。总摩擦转矩T由粘性摩擦转矩Tl和与负载相关的摩擦转矩Tv组成：

T=Tv+T1

(17)

(18)

式中，f0为轴承和润滑类型的指数，v为工作粘度，单位是cSt;n为轴承转速，单位是r/min;dm为轴承内径和外径的平均直径，单位是mm。

粘性摩擦转矩T1可以通过以下公式计算：

(19)

式中，f1为负载的一个因子，对于带机壳的径向轴承，f1的范围是0.0002(轻系列)至0.0004(重系列)[36]，Fmean为作用在轴承上的平均负载。

最后轴承损耗可以通过下式求出：

Pbearing=Tω

(20)

图10 样机负载实验平台

将电机额定负载下的损耗计算结果与试验结果进行对比，如图11所示。可以看出，通过单向耦合法与双向耦合法计算得到的电机总损耗分别为503.87 W，529.36 W，实验测试结果为548.9 W，误差分别为4.1%和1.5%，通过双向耦合法计算得到的电机损耗结果与验结果更为接近。

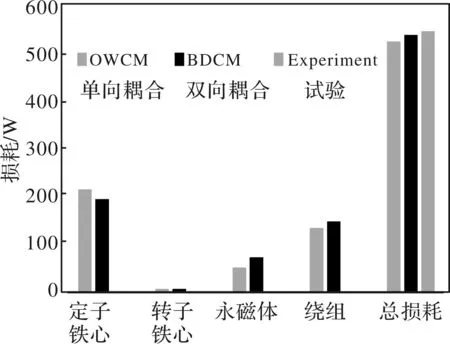
图11 样机损耗计算结果实验测试结果对比

4.2 额定负载温升测试及分析

对样机在20000 r/min下进行温升测试，电机端部绕组嵌入4个热敏电阻以测量局部温度。 计算结果与测试结果对比如表8所示。可以看出，由磁热双向耦合方法(方法C)计算得到的电机温升结果与测试值更加一致。20000 r/min时误差分别为2.9%，2.4%和2.3%，满足工程实际要求，试验结果证明了前文分析结果的准确性和有效性。

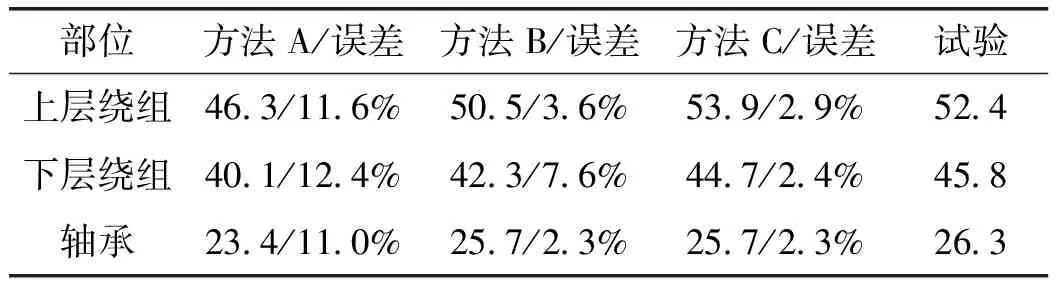
表8 电机平均温升计算结果对比 (单位：K)

5 结 论

在本文中，通过单向耦合法和双向耦合法对绕组和永磁体的温度相关特性对永磁同步电机的损耗和热特性的详细影响进行了全面研究，实验结果验证了电机在变频器供电下损耗和温升计算结果的有效性。与单向耦合法计算得到的电机总损耗相比，在考虑了绕组和永磁体的温度相关特性后，双向耦合法计算得到的电机总损耗增加了3.1%。同样，双向耦合法获得的最大温升比单向耦合法增加了 5.2%。双向耦合法计算的温升结果比单向耦合法得到的结果更接近实验值。当绕组和永磁体的温升超过40K时，双向耦合法的损耗和温升计算精度显著升高。