永磁同步电机转子涡流损耗优化及温升分析

刘国栋，张学义，王爱传，高 霆，李杰文，高志东，任爱冬，尹红彬

(1.山东理工大学 交通与车辆工程学院，山东 淄博 255000；2.山东五征集团有限公司，山东 日照 262306；3.潍坊市电机一厂有限公司，山东 潍坊 262100)

0 引 言

永磁同步电机具有高功率密度、高过载能力、高效率区间等优点，应用前景广阔。但绕组分布、定子齿槽和磁极形状等使永磁电机磁场内存在高次谐波，较强的高次谐波会在永磁钢和转子铁心中产生涡流损耗，从而引起转子温度升高，而较高的转子温度容易使永磁钢磁性减弱，甚至发生退磁现象，减低电机工作效率。因此，分析永磁同步电机内部磁场高次谐波磁场的影响因素，削弱高次谐波的幅值，对降低电机损耗，降低电机转子温度，提高电机工作效率有重要意义。

国内外学者已在该研究领域开展深入研究，并取得了一些成果，赵朝会[1]，陈阳生[2]等利用有限元计算法和磁场分析法研究了气隙长度、极弧系数和极对数对永磁同步电机气隙磁密的影响规律。Irina-Yu kru[3]等，周凤争[4]推导出考虑定子齿形状、转子不对称磁阻和铁心饱和的气隙磁通谐波的计算方法，并以此分析永磁同步电机涡流损耗。Wenjing-Hu[5]等，徐英雷[6]等采用非均匀气隙改善气隙磁场波形来减少气隙磁密畸变率，推导了气隙磁密的计算方法，并优化了转子偏心参数。在转子结构对涡流损耗影响方面，A.Cavagnino[7]等、Dominic A[8]等提出采用分块的永磁钢来减小转子涡流损耗。孔晓光[9]等，杜国华[10]等推导出电机损耗、热导和温度之间的解析方程并利用有限元法进行了稳态热分析，研究电机温升特性。

由分析可得，目前，国内外学者对电机气隙磁密及转子涡流损耗均开展了深入研究，但对涡流损耗与磁密谐波的影响规律研究较少，本文结合磁场谐波理论与二维有限元计算方法，从转子涡流损耗与气隙磁密谐波入手，研究电机主气隙长度、非均匀气隙结构参数等对涡流损耗及气隙磁密高次谐波的影响规律，并完成参数优化，达到降低电机涡流损耗，提高输出性能的目的。

1 永磁电机转子涡流损耗谐波分析

目前，永磁转子铁心多由硅钢片叠压而成，相邻的硅钢片之间存在间隙，涡流损耗几乎为零，假设转子铁心涡流损耗仅存在于每片硅钢片之中。单片硅钢片涡流损耗的物理模型如图1所示。

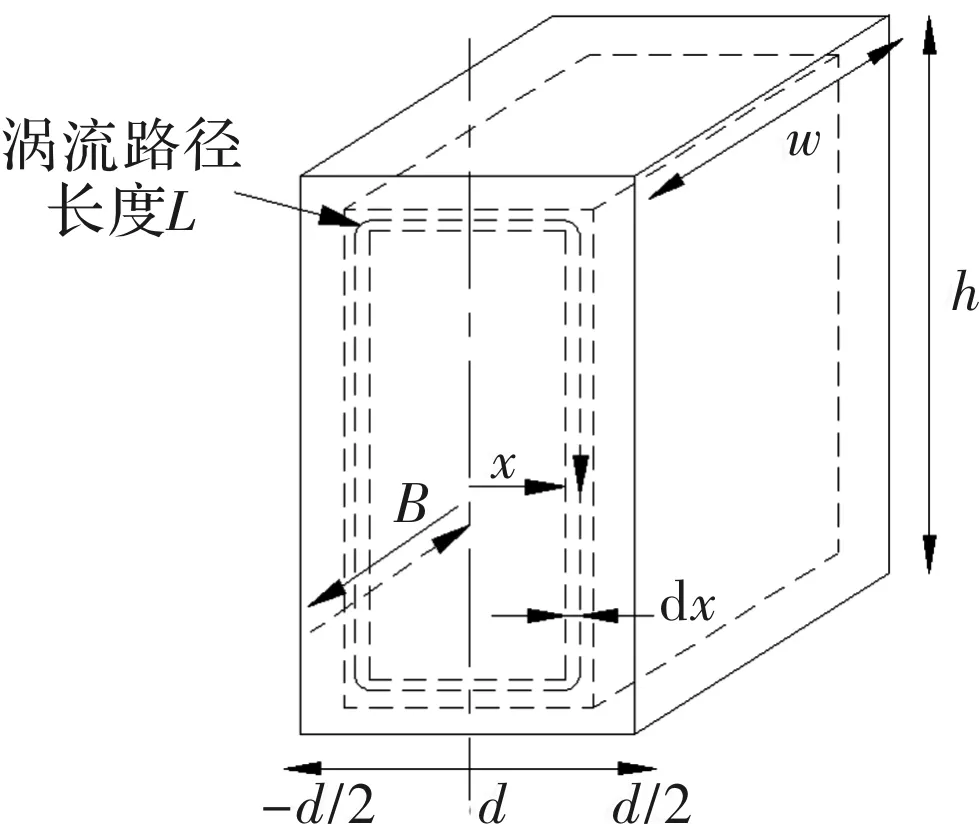
图1 硅钢片涡流损耗模型

当磁通密度B在图1中箭头方向穿过电阻率为ρ的硅钢片时，硅钢片产生的涡流损耗PFe,Ft可计算为

(1)

式中，dPFe,Ft为一定功率下涡流损耗微分；d、w、h分别为硅钢片宽度、高度和轴向长度；E为涡流磁通回路上电感电压有效值，可计算为

(2)

将式(2)带入式(1)可得

(3)

式中，V为硅钢片的体积V=d·w·h；f为电机频率。

从式(3)可看出，硅钢片产生的涡流损耗dPFe,Ft主要与硅钢片的体积V、电阻率、磁通密度B和电机频率f有关。其中，除磁通密度B外，其余均为整机性能参数和硅钢片材料参数，当永磁电机主要性能指标确定时，上述参数基本确定，因此，削弱转子涡流损耗，需从通入硅钢片的磁通密度B入手，由于不同位置转子铁心磁通密度不同，难以确定，但转子铁心磁通密度与主气隙磁通密度呈正比变化，因此，本文采用主气隙磁通密度Br代替转子铁心磁通密度Bt，并定义两者之间的关系为

Br=σrt·Bt

(4)

式中，σrt为转子磁场漏磁系数。

电机主气隙内沿着径向分布的主气隙磁通密Br可计算为

Br=F(x)·λ(x)

(5)

式中，F(x)为转子磁场在主气隙中的磁势，λ(x)为沿主气隙径向分布的气隙磁导。

分别对F(x)和λ(x)进行傅里叶分解，可得傅里叶变换后的主气隙磁密B(θ,t)表达式如下：

(6)

(7)

(8)

(9)

(10)

(11)

式中，Fv(θ,t)为傅里叶分解后的主气隙中的磁势；λ(θ,t)为傅里叶分解后的气隙磁导；fv为定子磁势谐波幅值；kg为电机磁饱和系数；k1=1,2,3；Λ0为气隙磁导不变部分；f0为基波磁势幅值；Λk1为转子表面磁导谐波幅值；v为定子磁势谐波极对数；vz为定子齿谐波极对数；ω为定子基波旋转角速度；Kc为卡特系数；Λ0为真空磁导率；t为定子齿距；l为定子齿径有效长度；μr硅钢片磁导率；bsc定子槽口宽度；δ为电机气隙长度；

由式(6)可得，主气隙磁密主要与主气隙参数有关，如定子槽口宽度bsc、主气隙长度δ等，改变定子槽参数和主气隙长度函数能改变主气隙磁密，进而改变电机转子涡流损耗。其中，改变主气隙长度函数的主要方法有采用非均匀气隙和定子斜槽两种方法，因此，可从影响转子涡流损耗的气隙磁密参数入手，研究定子槽口宽度、主气隙长度、非均匀气隙结构参数、定子斜槽参数与主气隙磁通密度和涡流损耗的规律。

2 转子涡流损耗优化参数分析

2.1 定子槽口宽度

以8极36槽5 kW永磁同步驱动电机为例，研究不同参数与转子涡流损耗的影响规律，利用有限元软件建立永磁电机三维模型如图2所示，电机的主要性能参数如表1所示。

图2 永磁电机三维模型

表1 电机主要性能参数

固定整机参数不变，取定子槽口宽度bsc为1.5～5 mm，步长为0.5 mm，仿真求解永磁同步电机主气隙磁密曲线如图3所示，对其进行傅里叶变换得3次、4次、5次、7次、8次谐波幅值变化曲线如图4所示。仿真求解不同定子槽口宽度时转子涡流损耗如图5所示。为了便于观察，主气隙磁密曲线中定子槽口宽度的步长取1.0 mm。

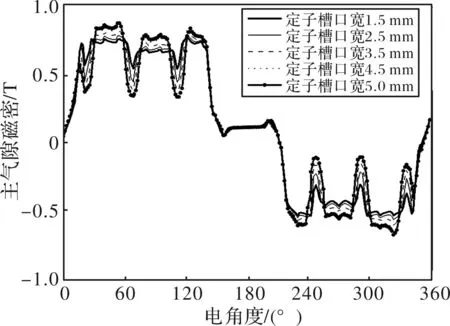
图3 不同定子槽口宽度的主气隙磁密曲线

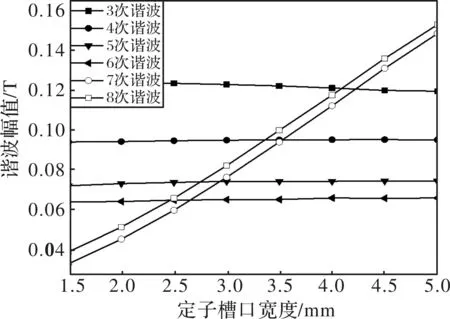
图4 不同定子槽口宽度的主气隙磁密谐波幅值变化曲线

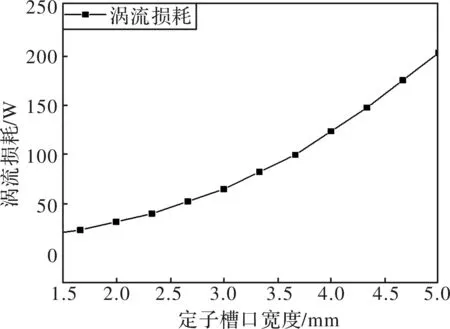
图5 转子涡流损耗变化曲线

由图3可得，当定子槽口宽度增大时，主气隙磁密曲线峰值增大，但波峰之间的凹陷程度增大，磁密曲线畸变增加，由各次谐波幅值变化图也可看出，随定子槽口宽度增大，除3次谐波有小幅度降低外，其他谐波幅值均呈上升趋势。由图5可得，随着定子槽口宽度增大转子涡流损耗呈上升趋势。考虑到电机定子绕组铜线直径，本文中定子槽口宽度取2 mm。

2.2 气隙长度

当气隙长度δ取0.3～1.1 mm，步长为0.1时，仿真得不同气隙长度永磁同步电机主气隙磁密变化曲线如图6所示，对其进行傅里叶变换后得2次、3次、4次、5次、6次、7次、8次谐波幅值变化曲线如图7所示。

图6 主气隙磁密变化曲线

图7 主气隙磁密谐波幅值变化曲线

由图6可得，当气隙长度增大时，主气隙磁密峰值降低，波形中毛刺减少，谐波幅值降低，曲线更为平滑。由图7可得，除9次谐波幅值略有上升外，其他谐波幅值均呈下降趋势，5、6次谐波下降幅度最为明显。仿真求解不同气隙长度转子涡流损耗变化曲线如图8所示，随着气隙长度增大，转子涡流损耗逐渐降低。考虑到电机的加工成本与制作工艺，本文中气隙长度取0.7 mm。

图8 转子铁心涡流损耗曲线

2.3 偏心距

非均匀气隙结构是使永磁结构对应转子外圆弧线的圆心偏离均匀气隙转子圆心，形成非均匀主气隙的偏心转子结构。该结构转子表面呈以磁极弧长为周期的规律性弧形分布，可有效改变主气隙长度函数，影响主气隙磁密波形，从而影响转子涡流损耗，非均匀气隙偏心转子结构示意图如图9所示。

图9 非均匀气隙偏心转子结构示意图

如图9所示，均匀气隙转子的外圆以O为圆心,非均匀气隙偏心转子外圆弧面以O1为圆心，O1O的距离定义为转子偏心距h，显然h值越大，转子的非均匀程度越高。考虑到偏心距h过大会降低主气隙磁密。因此，设置转子偏心距h的区间为0～9 mm，步长为0.75 mm，仿真得不同偏心距h时的主气隙磁密曲线如图10所示。傅里叶变换后得3次、4次、5次、7次、8次、9次谐波幅值变化曲线如图11所示。

图10 主气隙磁密变化曲线

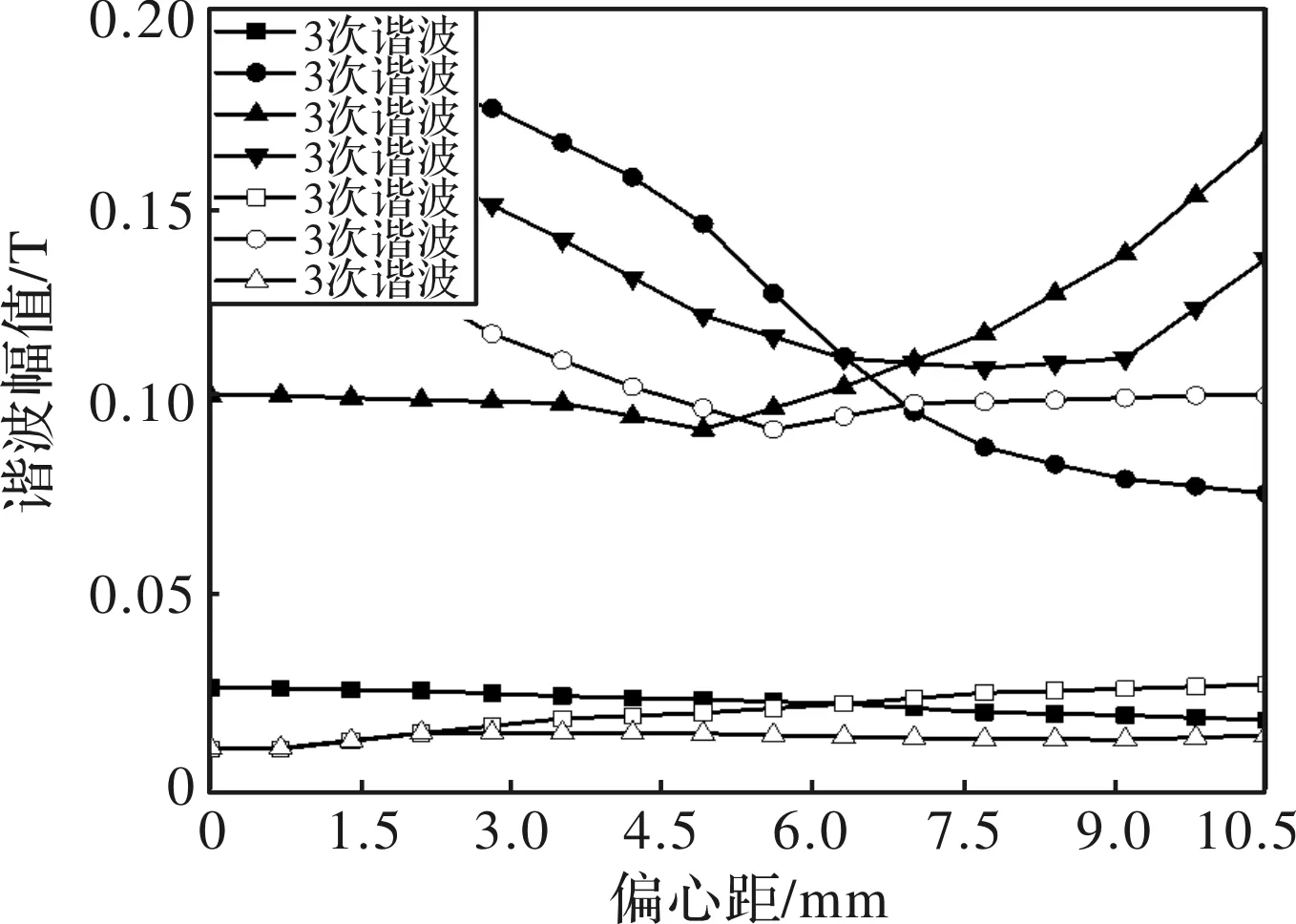
图11 谐波幅值变化曲线

由图10可得，随着偏心距h增大，电机主气隙磁密曲线峰值增大，波形两侧倾斜度增大，更趋于正弦曲线。由图11可得，随着偏心距h的增大，4次谐波呈下降趋势，5次、6次、8次谐波先减小后增大，其他各次谐波幅值变化不明显。不同转子偏心距时转子铁心涡流损耗曲线如图12所示，由图12可得，随着转子偏心距的增大，转子涡流损耗先减小后增大，在偏心距为5.25 mm处涡流损耗最小。因此，本文中转子偏心距取5.25 mm。

图12 转子铁心涡流损耗

2.4 定子斜槽角度

定子斜槽能够引起主气隙轴向长度函数变化，进而影响主气隙磁通密度，本文设置定子斜槽角度为0°～22°，步长为2°，仿真求解永磁同步电机主气隙磁密的3次、4次、5次、6次、7次、8次、9次谐波幅值变化曲线如图13所示。由图13可得，随着定子斜槽角度的增加，除了9次磁谐波幅值略有上升外，其他3次、4次、5次6次、7次、8次谐波幅值总体呈下降趋势。

图13 谐波幅值变化曲线

不同定子斜槽角度时转子铁心涡流损耗曲线如图14所示。随着定子斜槽角度的增大，转子铁心涡流损耗呈下降趋势，在定子斜槽角度为8°时下降的速度最快，当定子斜槽在18°时下降速率趋于平缓，涡流损耗最小，因此，本文中定子斜槽角度取18°。

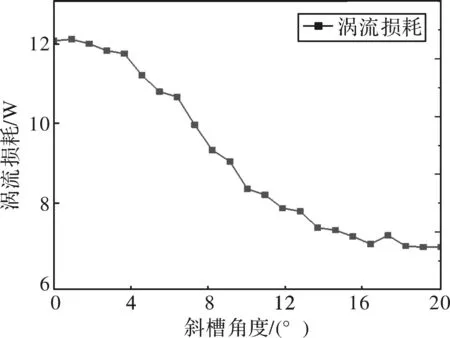
图14 转子铁心涡流损耗

3 优化结果分析与温升验证

以减少涡流损耗，提高主气隙磁密正弦性为目标，优化永磁同步电机定子槽口宽度、气隙长度、转子偏心距、定子斜槽角度等参数，优化结果如表2所示。建立优化后的仿真模型，求解优化前后的永磁电机主气隙磁密曲线如图15所示，各次谐波幅值如图16所示。

表2 电机参数优化结果

图15 优化前后主气隙磁密曲线

图16 优化前后主气隙磁密谐波幅值

由图15和图16可得，优化后的永磁同步电机主气隙磁密曲线正弦度增强，毛刺减少，平滑度提高，4次谐波幅值降低了86.7%，6次谐波降低了57.5%,9次谐波降低了76.7%。优化前后累计前30次谐波正弦畸变率分别为30.72%和19.26%。主气隙磁密波形正弦性得到明显改善。由图17可得优化后永磁同步电机转子涡流损耗显著降低，均值为8W，与优化前相比降低了39.6%。

图17 优化前后转子涡流损耗

通过Maxwell/workbench耦合仿真建立了永磁同步电机的温升模型，将Ansys/maxwell电磁仿真中的损耗导入到升温模型中，分别仿真永磁同步电机优化前后在额定功率下运行一个小时后的转子温度场云图，如图18所示。

图18 额定功率下永磁同步电机转子温度场分布云图

由图18可得，优化后的转子铁心平均温度显著降低，温差为4.18 ℃，其中，转子磁极弧线对应的转子表面温度降低了5.39 ℃；同时，优化后永磁钢的温度也明显降低，永磁钢朝向转子外边的一面温度降低了4.97 ℃。表3为Sm2co17、NdFeB、Alnico在不同温度下的磁通变化表，由表3可知，随着温度的升高，永磁体的磁通读数减小，即磁性降低。减小转子涡流损耗，降低永磁体温度，提高了永磁体的磁性，提高了电机的效率。

表3 不同种类永磁体磁通读数随温度变化表

4 结 语

本文基于永磁电机转子涡流损耗和主气隙磁密表达式的解析计算，确定了电机转子涡流损耗的主要影响因素，研究了定子槽口宽度、气隙长度、转子偏心距和定子斜槽角度对永磁同步电机转子涡流损耗的影响，优化设计出3相8极36槽永磁同步电机最优参数，优化后转子涡流损耗降低了39.6%，且优化后主气隙磁密高次谐波幅值降低，波形正弦畸变率降低到19.26%。同时，对优化前后电机进行磁-热耦合分析，优化后转子铁心、永磁钢发热降低，永磁钢磁性提高，电机输出特性显著提升。